简化导航算法在导弹飞行试验安全分析中的应用

甄昕，丁力军，辛庆伟

（1.92941部队；2.92493部队，辽宁葫芦岛125001；3.海军航空工程学院接改装训练大队，山东烟台264001）

简化导航算法在导弹飞行试验安全分析中的应用

甄昕1，丁力军2，辛庆伟3

（1.92941部队；2.92493部队，辽宁葫芦岛125001；3.海军航空工程学院接改装训练大队，山东烟台264001）

安全分析是反舰导弹飞行试验前必须开展的一项重要工作，安全分析以导弹弹道数据为基础，而弹道仿真模型获取不易。基于此，提出了一种可用于反舰导弹飞行试验安全分析并能取代弹道仿真的简化导航算法，对其实现原理和实现方法进行了阐述。经过实践检验，此种算法计算简单、效率高，其精度满足导弹飞行试验安全分析要求。

反舰导弹；飞行试验；安全分析；威胁概率

靶场进行反舰导弹飞行试验，首先要选择试验航区，并且要对试验航区内或周边的石油钻井平台、大型岛礁以及岸上目标可能造成的安全威胁作出评估，也就是要进行所谓的安全分析。

进行安全分析必须明确导弹飞行轨迹，也就是要确知导弹的相关弹道数据。目前，从解算导弹弹道角度而言，反舰导弹飞行试验安全分析可分为2种：一种是从研制单位获取弹道方程及相关气动参数进行弹道仿真，来得到导弹飞行轨迹的安全分析方法。此种方法的优点是精度高，缺点是弹道仿真模型难以获取，即使获取了仿真模型，编程计算也相当繁琐，不是短时间能够完成的[1]，而飞行试验安全分析是开展飞行试验必不可少的前提性工作，时间紧迫；另外一种方法即工程近似法，就是本文提出的基于简化导航算法来模拟导弹飞行轨迹的工程近似法。实践表明，此种方法易于理解，计算简单，通用性强，效率高且精度满足要求。

1 基本原理

导弹只有在其制导系统的导引下，才有可能飞向目标，一般反舰导弹在导航坐标系确立后，通过解算导航方程并进行相应的误差补偿，得出导弹飞行所需的导航信息，如导弹经度、纬度、目标方位角、导弹姿态角以及沿3个方向的加速度、速度等[2-3]。解算导航方程的过程就是在进行弹道计算，其模型复杂，计算繁琐，输入、输出参数众多，而在导弹飞行试验安全分析中，一般只需要知道导弹飞行过程中的位置信息（任一点的经纬度和方位角），且输入参数很少，因而有必要寻找一种能够较精确解算导弹飞行过程中位置信息的简化导航算法，以提高试验效率。

反舰导弹在地球表面附近运动，实际上是沿椭球面运动（地球近似椭球），由于反舰导弹射程较小，飞行高度低，其在空中的运动轨迹完全可以用参考椭球面上的大地线来近似[4-5]。

所谓大地线，就是椭球面上2点间的最短线，而且它是唯一的[6]。在理想状态下，不进行扇面发射和航路规划的反舰导弹在空中的飞行轨迹在椭球面上的投影，应该和椭球面上连接导弹发射点和目标点的大地线近似重合[7]。因此，在对反舰导弹飞行试验进行安全分析时，用参考椭球面上的大地线来近似代替其在空中的运动轨迹，就是简化导航原理的出发点。

简化的导航算法正是基于简化导航原理，其核心就是贝塞尔大地问题正解公式[8]。

如图1所示，已知P1点大地坐标(L1,B1)及其大地方位角α1，P1点至P2点的大地线长度为s，N为真北方向。计算P2点的大地坐标(L2,B2)和大地线在P2点的大地反方位角α2，称为大地问题正解。

由球面三角学可知，球面三角公式都是用角度的三角函数表示的，球面上距离的大小与解算球面三角形的精度无关。又因为地球椭球的扁率很小，若将其上的诸元素（经度、纬度、边长及方位角）化为球面上对应元素并均用角度表出时，其对应的用角度表出的改正数一定是不大的，而且也和距离几无关系。因此，贝塞尔公式解算大地问题的基本原理就是按一定的投影条件，建立椭球面上的元素和球面上对应元素间的投影关系，通过解算球面三角形的方法而使问题得解。用此方法求解，其终点经纬度及大地方位角可精确至0.003″，而且适用于长距离解算，具体计算公式详见参考文献[8]。

图1 大地问题正解示意图Fig.1 Positive solution schematic diagram ground question

在反舰导弹飞行试验中，知道了导弹发射点O的经纬度(L0,B0)，导弹射向α1，取解算步长h为100 m，运用贝塞尔大地问题正解公式不断进行迭代计算，就可给出导弹飞行轨迹任一位置的经纬度(L2,B2)和大地线反方位角α2（迭代时要将α2换算为大地线方位角），这样就可以近似模拟导弹飞行过程中的位置信息。在实际应用过程中，导弹射程数百千米，运用贝塞尔大地问题正解公式经过迭代（h=100 m）解算得到的靶船经纬度，与通过弹道仿真给出的靶船经纬度相比，经度相差不到2'、纬度相差不到1'（等同于在以研制单位给出的靶船位置为中心、半径4 km的圆内），在精度上能够满足导弹飞行试验安全分析的要求。

2 算例分析

假设某型反舰导弹在O(L0,B0)发射，射向为α1，如图2所示，已知导弹射程dk，动力航程为dl，平均速度为v，试计算导弹对陆地威胁概率。

图2 导弹飞行试验区域示意图Fig.2 Regional schematic diagram of missile flying test

假设反舰导弹只有在导弹故障且安控失效的情况下，才可能对陆地构成威胁。又假设导弹有2种主要故障模式即失控无偏坠毁和失控偏航坠毁，只有失控偏航坠毁才能对陆地构成威胁。如果导弹在飞行弹道某点出现故障，失控偏航坠毁导弹的散布服从正态分布，散布范围是以导弹射向为中心线的前半圆，不会对后方构成威胁；从对陆地最大威胁情况考虑，导弹发生故障后以100%的概率飞完剩余航程（动力航程—已飞距离）。

2.1 建立导航坐标系

首先，将导弹弹道上某点的大地坐标(L,B,H)转换为地心空间直角坐标(x,y,z)；再通过坐标平移和转换，可将地心空间直角坐标(x,y,z)转换为以此点为原点的导航坐标系(X,Y,Z)，此坐标系X轴与真北所成角度为α，方向指向目标一侧，Y轴与水平面垂直、向上，Z轴在水平面内与X、Y轴成右手法则[9]。它可以近似模拟反舰导弹真实飞行中的游动方位坐标系，其在发射点与导弹发射坐标系重合[10]。

2.2 威胁原理推导

在图2上沿海岸线上取2点M(LM,BM)，N(LN,BN)，经坐标平移和转换后得到M(Z1,X1)，N(Z2,X2)，见图3，使直线MN近似代替海岸线。取步长h=100 m（也可取其他值），则导弹发射后，弹道上间隔100 m的任一递推点Ki的大地坐标和大地反方位角可由贝塞尔大地问题正解公式得到。再经过坐标平移和转换，可建立以Ki点为原点的导航坐标系。以此坐标系原点为圆心，r为半径画圆（r=动力航程-已飞距离），如果此圆与直线MN有2个交点，那么导弹可能对陆有威胁，否则没有威胁。

图3 对陆威胁概率计算示意图Fig.3 Calculation schematic diagram of land threat probability

如图3所示，经推导，计算圆Ki与直线MN交点P1、P2及角度φ1、φ2的公式如下。

直线MN方程：

圆Ki方程：

解联立方程（1）、（2），可得直线MN和圆Ki的交点P1(F,AF+B)、P2(G,AG+B)，且有坐标参数值如下：

在满足D2＞4CE条件下，有式（3）~（6）成立。

当AF+B＞0与AG+B＞0同时成立时，有：

当AF+B＞0与AG+B≤0同时成立时，有：

当AG+B＞0与AF+B≤0同时成立时，有

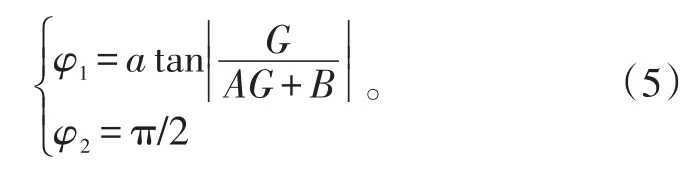
当AG+B≤0与AF+B≤0同时成立时，Wi=0（导弹不会对陆地造成威胁）。

在D2≤4CE时，圆与直线MN有交点个数不超过1个，Wi=0（导弹不会对陆地造成威胁）。

运用弹道逐点积分原理（具体原理及若干计算公式详见参考文献[11]），可以得到导弹在Ki点故障落入到陆地的概率Pi。再由导弹在Ki点故障的概率Fi1和安控系统在Ki点失效概率Fi2，则Ki点对陆地的威胁概率为：Wi=PiFi1Fi2。导弹飞完全程对陆地的总威胁概率为

计算导弹对海上钻井平台和岛礁的威胁概率比计算对陆威胁概率要简单，只要给出钻井平台或岛礁的大地坐标和它们的半径数值，运用弹道逐点积分原理就可求得，其坐标系的建立和总威胁概率W的计算公式与对陆威胁概率计算一致。

2.3 编程计算

计算对陆威胁概率W的程序框图见图4。

图4 计算导弹对陆威胁概率程序框图Fig.4 Program diagram of calculation willile land threat probability

以上算例采用Matlab语言只需近百行源程序，且编程计算方便快捷，结果精度满足试验要求，如采用全弹道仿真方法（在获得弹道仿真模型的前提下）进行对陆地威胁概率计算，编程计算就繁琐得多，至少需近千行Matlab源程序[12]，花费大量的时间和人力，其效费比要低得多。假设发射点经纬度为（121.532 7°,41.091 9°），射向为156°，步长100 m，射程290 000 m，，用以上方法编程计算可得目标经纬度为（122.876 2°,38.708 9°）；用弹道仿真方法得到的目标经纬度为（122.869 3°,38.692 1°）。经计算2个目标点距离为4 000 m，满足导弹飞行试验安全分析要求。

3 结论

如反舰导弹有扇面发射或航路规划，也可用贝塞尔大地问题正解公式求解，只是在导弹飞行弹道上选几个已知经纬度和方位角的转折点，将原来一条大地线变为几条首尾相连的大地线就可以了。采用以贝塞尔大地问题正解公式为核心的简化导航算法，只要知道导弹发射点经纬度、导弹射向、目标点经纬度就可以进行导弹飞行位置信息模拟，并通过弹道逐点积分方法进行导弹威胁概率解算，可得到精确满足要求安全分析结果，这是一种可行的工程近似方法。

[1]王精业.仿真科学与技术原理[M].北京：电子工业出版社，2012：6-56. WANG JINGYE.Science and Technology Theory of Simulation[M].Beijing：Electronic Industry Press，2012：6-56.（in Chinese）

[2]杨军.导弹控制原理[M].北京：国防工业出版社，2010：2-15 YANG JUN.Missile control theory[M].Beijing：The National Defense and Industry Press，2010：2-15.（in Chinese）

[3]潘荣霖.飞航导弹自动控制系统[M].北京：宇航出版社，1991：56-59. PAN RONGLIN.Missile auto control system[M].Beijing：Aero space Press，1991：56-59.（in Chinese）

[4]德米特里耶夫斯基.外弹道学[M].韩子鹏，译.北京：国防工业出版社，2000：9-35. DMITRIYEVSKIY.The outer ballistic theory[M].Traslated by Han Zipeng.Beijing：The National Defense and Industry Press，2000：9-35.（in Chinese）

[5]孔祥云，郭际明，刘宗泉.大地测量学基础[M].武汉：武汉大学出版社，2010：6-69. KONG XIANGYUN，GUO JIMING，LIU ZONGQUAN. The base theory of the ground measuring[M].Wuhan：Wuhan University Press，2010：6-69.（in Chinese）

[6]胡明城.现代大地测量学理论及其应用[M].北京：测绘出版社，2003：12-23. HU MINGCHENG.The modern theory and application of the ground measuring[M].Beijing：Measuring Press，2003：12-23.（in Chinese）

[7]韩子鹏.弹箭外弹道学[M].北京：北京理工大学出版社，2008：4-41. HAN ZIPENG.Outer ballistic theory of missile and rocket [M].Beijing：Beijing Theory and Industry University Press，2008：4-41.（in Chinese）

[8]朱华统，黄继文.椭球大地计算[M].北京：解放军出版社，2001：79-84. ZHU HUATONG，HUANG JIWEN.The computation of the ground of the elliptic sphere[M].Beijing：PLA Press，2001：79-84.（in Chinese）

[9]罗建军.组合导航原理及应用[M].西安：西北工业大学出版社，2012：3-11. LUO JIANJUN.The Theory and Application of Composed Navigation[M].Xi'an：North West Industry University Press，2012：3-11.（in Chinese）

[10]孟秀云.导弹制导与控制系统原理[M].北京：北京理工大学出版社，2003：3-43. MENG XIUYUN.The missile guidance and control system theory[M].Beijing：Beijing Theory and Industry University Press，2003：3-43.（in Chinese）

[11]曲宝中，孙晓峰，李守秀.海军战术导弹试验与鉴定[M].北京：国防工业出版社，2006：223-227. QU BAOZHONG，SUN XIAOFENG，LI SHOUXIU.Navy tactical missile test and evaluation[M].Beijing：The National Defence and Industry Press，2006：223-227.（in Chinese）

[12]DAVID ALLERTON.飞行仿真原理[M].刘兴科，译.北京：电子工业出版社，2012：8-26. DAVID ALLERTON.Flying simulation theory[M].Translated by LIU XINGKE.Beijing：Electronic Industry Press，2012：8-26.（in Chinese）

Application of Simplified Navigation Algorithm for the Safety Analyss During the Missile Flying Test

ZHEN Xin1,DING Li-jun2,XIN Qing-wei3
（1.The 92941stUnit of PLA;2.The 92493rdUnit of PLA,Huludao Liaoning 125001,China;3.Training Brigade of Equipment Acceptance and Modification,NAAU,Yantai Shandong 264001,China）

Safety analysis is an important task that must be finished before launching anti-ship missiles.The missile ballistic simulation data is the basic part for the safety analysis,but the missile ballistic simulation is difficult for us to complete. Because of this,a kind of simplified navigation algorithm for the safety analysis in the anti-ship missile flying test was put forword,and its principle and method was elaborated in this paper.This algorithm had some advantages such as simple computation,high efficiency.The result of its actual application was satisfied with the safety analysis in the anti-ship missile flying test.

anti-ship missile;flying test;safety analysis;threat probability

TJ760.6+28

A

1673-1522（2014）01-0005-04

10.7682/j.issn.1673-1522.2014.01.002

2013-10-10；

2013-11-25

甄昕（1970-），男，高工，大学。