采用加速度计和磁强计的水平测斜仪校准方法
2014-07-06张先韬黄麟森
张先韬,黄麟森
(1.中国煤炭科工集团重庆研究院,重庆 400039;2.瓦斯灾害监控与应急技术国家重点实验室,重庆 400039)
在煤矿钻孔施工过程中,为了达到钻孔施工要求,定向钻孔和钻孔轨迹测量成为目前控制钻孔走向与绘制钻孔轨迹的重要技术。在钻孔施工过程中确定出钻进倾角和方位角,以及钻进时的钻头位置,可以方便地绘制出钻孔轨迹和调整钻进方向。因此,提高测斜仪的测量精度成为钻孔测斜技术研究的关键[1-3]。煤矿用近水平钻孔测斜仪主要使用加速度计和磁强计进行数据测量,而这种测斜仪测量精度的提高依赖于对传感器自身误差和安装误差的校准技术。目前煤矿、石油以及其他行业使用加速度计和磁强计的测斜仪校准,普遍用特殊位置法进行误差补偿,校准精度有待提高[4-13]。近几年,许多国内外学者均在探索更加简便的校准方法,并对加速度计和磁强计分别进行校准[6,7,9,14-16]。在同时使用加速度计和磁强计的测斜仪中,对于误差校正需要同时考虑加速度计和磁强计,比单一类型传感器的误差补偿复杂得多[1-3,5,10-12]。本文以自主研发的煤矿近水平钻孔测斜仪硬件为基础,研究了使用软件计算提高测斜仪精度的方法。
1 系统组成
本文研究内容基于笔者所在院校自主研发的煤矿近水平钻孔测量系统,成套系统主要包括测斜仪、测量软件、计算机等。
水平测斜仪主要由传感器、测量电路、保护壳体等部分组成。传感器分别使用3个加速度计、3个磁强计,同一类型的传感器按照空间直角坐标系近似正交安装。通过3个加速度计的输出数值计算倾角和重力工具面角,通过磁强计和加速度计的输出数值计算方位角,从而获得空间中测斜仪所在点的姿态。测量软件获取到测点姿态后根据数据计算出该测点的空间相对位置,绘制并显示出轨迹曲线。
2 校准方法及实现
在传感器安装完毕后,由于传感器自身的原因,会产生零偏误差;3个传感器灵敏度不相同在参与倾角和方位角计算时也会产生误差;3个传感器安装时如不能保证严格正交,也会在计算时产生误差[1-3]。精确测量的理论依据是:单个加速度计无零偏影响且灵敏度相同;3个加速度计两两完全正交,加速度计所在坐标系与磁强计所在坐标系对应轴完全平行[8,10]。提高测斜仪的精度就需要尽可能地消除这3种误差的影响,其校准数学模型如下所示。由于加速度计和磁强计的安装和校准过程类似,下面以加速度计为例进行说明。
2.1 误差产生机理分析及误差补偿数学模型
设每种类型3个传感器分别为x,y,z;3个加速度计的对应输出分别为Ax,Ay,Az;3个磁强计的对应输出分别为Mx,My,Mz;进行误差补偿后可以精确计算倾角和方位角等的对应数值分别为Gx,Gy,Gz,Bx,By,Bz。实际安装位置传感器的输出与对应坐标轴一般不重合,传感器输出与误差补偿后的矢量图关系如图1所示。其中:Og-AxAyAz和Ob-MxMyMz为传感器实际输出的矢量;Og-GxGyGz和Ob-BxByBz为传感器输出进行误差补偿后的矢量,理想状态下误差补偿后各个矢量均沿着测斜仪理论上的仪器坐标系Og-XYZ坐标轴方向。
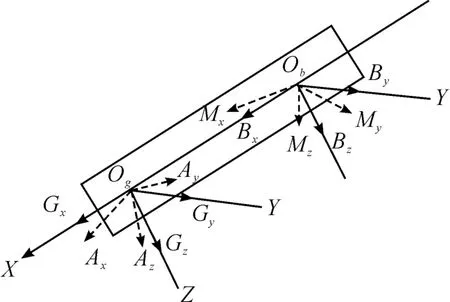
图1 传感器输出校准前与校准后关系示例
结合图1并根据误差产生机理的不同可将直接影响测斜仪测量精度的误差分为4类:零偏误差、灵敏度误差、正交性误差、坐标系不重合误差。
2.1.1 误差分析
1)零偏误差
测斜仪使用的传感器由于模拟电路和A/D转换的零点为传感器的绝对位置零点,使得输出矢量对称的坐标系零点产生零点偏移误差,在数学模型中是由对称位置的输出矢量不对称造成的误差。加速度计零偏误差补偿的数学模型为:
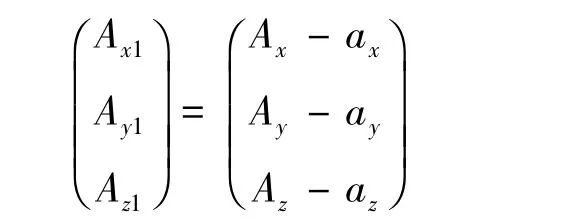
其中:Ax,Ay,Az为对应加速度计的输出数值;ax,ay,az为对应加速度计的零偏数值;Ax1,Ay1,Az1为对应加速度计输出数值消除零偏后的数值。磁强计的零偏误差补偿模型与加速度计的零偏误差补偿模型一致。
2)灵敏度误差
测斜仪获取精确结果时,需保证同一类型的传感器量程一致。若量程不一致则会造成同一位置不同传感器的输出值不同,即灵敏度不同,从而产生测量误差。灵敏度误差就是由于传感器各轴的灵敏度不同、测量信号的放大电路特性不完全相同而引起的测量误差,在数学模型中是各坐标轴矢量长度最大值不同造成的误差。加速度计灵敏度误差补偿的数学模型为:
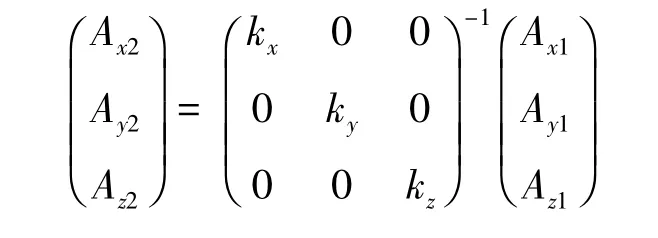
其中:Ax2,Ay2,Az2为对应加速度计输出消除灵敏度误差后的数值;kx,ky,kz为对应加速度计的灵敏度补偿因子;Ax1,Ay1,Az1为对应加速度计输出消除零偏误差后的数值。磁强计的灵敏度误差补偿模型和加速度计灵敏度误差补偿模型一致。
3)正交性误差
测斜仪3个加速度计(或磁强计)各轴间的正交性误差是由安装或制造过程中传感器的测量轴无法保证两两完全正交所引起的,在数学模型中是由坐标轴不正交造成的误差。在图1中,Og-AxAyAz的各轴两两之间的不正交产生加速度计的正交性误差;Ob-MxMyMz的各轴两两之间的不正交产生磁强计的正交性误差。正交性误差在计算时直接导致测斜结果的不准确。为了消除正交性误差,设图2中O-X'Y'Z'为消除正交性误差后的矢量所在坐标系为消除正交性误差之前的矢量方向,以x传感器输出的矢量方向为空间直角坐标系的Z轴基准建立坐标系O-X'Y'Z'。根据几何投影原理,设角[Y0OY']为α、角[Z'OH]为 β、角[Z0OH]为 γ。

图2 消除正交性误差矢量关系示意
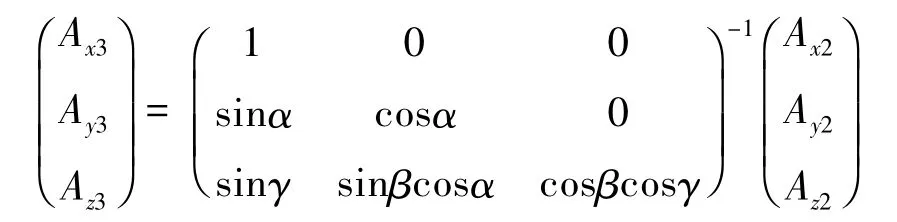
其中:Ax3,Ay3,Az3为对应加速度计输出消除正交性误差后的数值,各自的矢量方向分别对应为对应加速度计输出消除灵敏度误差后的数值,各自的矢量方向分别对应分别为图2所示角度值。
进行正交性误差补偿的过程使角度α,β,γ逐渐减小至零,由α,β,γ→0可得:
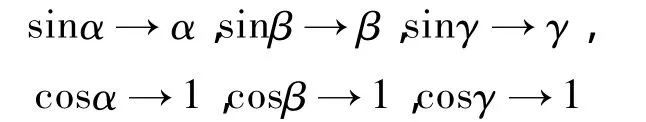
从而可以将正交性误差补偿模型化简为:
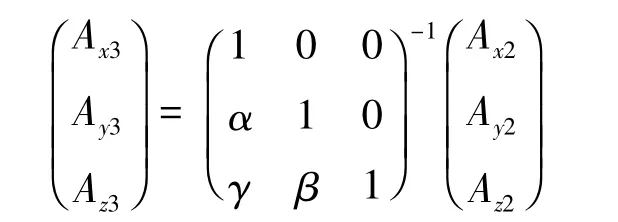
4)坐标系不重合误差
在同时使用加速度计和磁强计的测斜仪中,为保证测量结果的准确性,必须使传感器输出矢量的坐标系和仪器坐标系尽可能地重合,而这种不重合造成的误差即为坐标系不重合误差。如图1所示,要获得精确的测量结果,误差补偿后输出矢量坐标系Og-GxGyGz、Ob-BxByBz需与仪器坐标系Og-XYZ重合。3个坐标系重合时,由测斜仪得到的测量结果才能准确的对应设备放置状态的实际倾角、方位角、工具面角的数值。在图3中,设坐标系O-XYZ为仪器坐标系,O-X'Y'Z'为传感器输出消除正交性误差后的矢量所在的坐标系;设 角 [X'OX]为 θ、角 [Y'OY]为 φ、角[Z'OZ]为δ,这3个角度是消除前3种误差后的矢量所在坐标系与仪器坐标系对应轴的夹角。在实际安装时,产生的这3个夹角均为小角度,可以通过坐标变换使坐标系O-X'Y'Z'与O-XYZ重合,从而消除坐标系不重合产生的误差。在进行坐标旋转变换时,这3个夹角即为旋转变换的旋转角。

图3 坐标系不重合示例
根据图3所示,加速度计的坐标系不重合误差补偿的数学模型为:

其中:Gx,Gy,Gz为对应传感器输出消除上面4种误差后的数值;θ,φ,δ为上面所述的二面角;Ax3,Ay3,Az3为对应传感器输出消除正交性误差后的数值。由于传感器安装时的姿态能够保证θ,φ,δ均为小角度,校准过程中3个角度不断减小直至等于零时完成误差补偿。根据θ,φ,δ→0有:
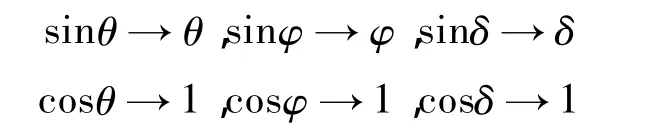
可以将对应的量进行近似,从而把模型化简为:
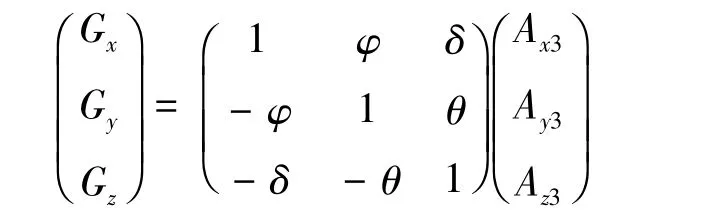
在进行坐标系旋转时,以图1中仪器坐标系O-XYZ为唯一固定坐标系。加速度计和磁强计消除前3种误差后均向坐标系O-XYZ进行旋转。磁强计坐标系旋转的模型和加速度计坐标系旋转的模型一致。
2.1.2 误差补偿数学模型
根据以上分析的传感器的4种误差,可以对这些误差进行复合处理,在进行最终误差补偿时可通过如下模型进行误差消除:
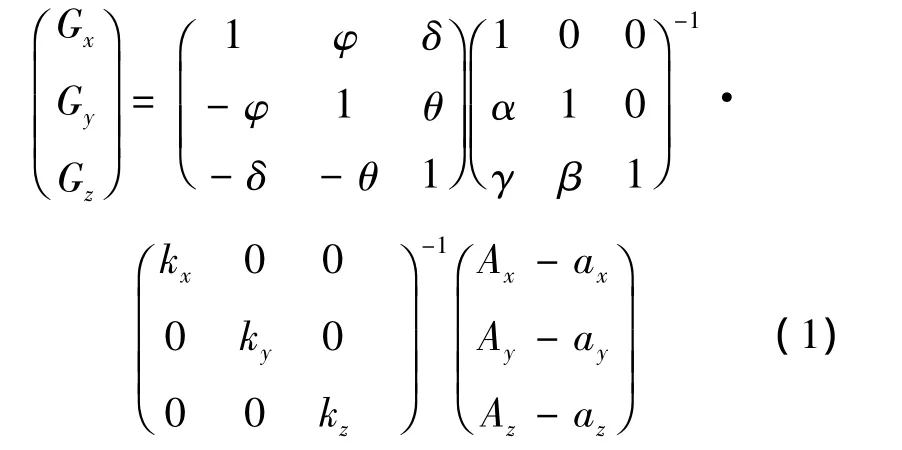
为了简单表达最终参与计算的参数,将上面模型整理成如下形式:
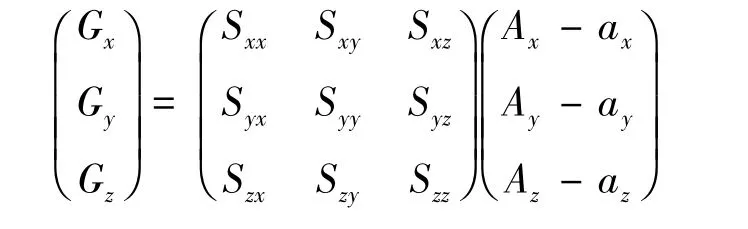
简记为 G=S(A-a),其中:ax,ay,az为对应传感器的零偏;Sxx的作用是将x传感器的输出向仪器坐标系轴投影并调整投影大小,是x加速度计的灵敏度因子;Sxy的作用是将y传感器的输出向空间直角坐标系X轴投影并调整投影大小,包含正交因子、灵敏度因子、坐标系不重合因子的综合作用;Syx的作用是将x传感器的输出向空间直角坐标系Y轴投影并调整投影大小,包含正交因子、灵敏度因子、坐标系不重合因子的综合作用;Sxz,Szx,Syy,Syz,Szy,Szz的作用由此类推。在进行误差补偿的实际操作时,对不同误差需按照上面的误差分析过程中的各种误差,计算对应的补偿参数,按照式(1)进行误差补偿系数的复合。
2.2 校准算法
上面的数学模型求解的关键在于使用适当的方法进行模型求解,以获取高精度的计算结果。提高测量精度有2点要求不容易实现:第一是传感器输出正交;第二是加速度计坐标系、磁强计坐标系、仪器坐标系3个坐标系重合。这2点是提高测斜仪精度的关键点,也是计算校准参数的难点。在研究中,可以将不同误差分离出来,使用不同算法进行各种误差补偿参数的独立求解,使用可靠的方法对不同误差补偿参数进行高精度求解。
2.2.1 椭球拟合算法获取零偏
球心不在原点的椭球曲面的标准方程为
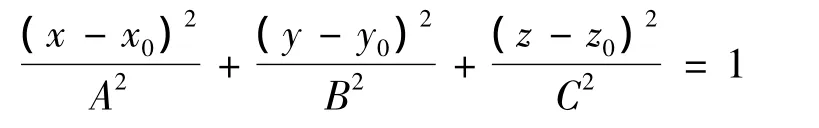
其中:(x0,y0,z0)球心即为传感器的零偏;1/A,1/B,1/C对应传感器的灵敏度因子。
二次曲面的一般方程为
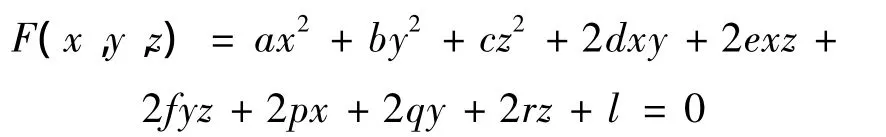
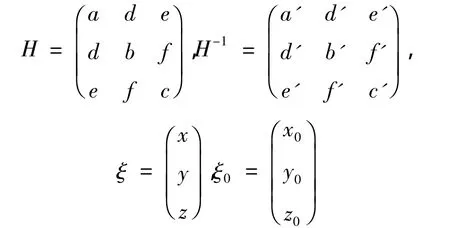
根据传感器的工作原理,同一类型的3个传感器按照空间两两正交安装且没有任何误差时,测斜仪在任意姿态时传感器输出的3个矢量合成为一个固定的矢量。对加速度传感器而言,这个合成矢量即为当地的重力加速度或与其成固定关系的一个值;对磁强计而言,若无外部磁干扰或磁干扰和忽略不计,则这个合成矢量为当地的地磁场强度或与其成固定关系的一个值。不妨设这个矢量为,则根据椭球面方程和一般二次曲面方程,可得椭球面方程为

将式子整理对比得到,椭球面的球心即对应传感器的拟合零偏为:
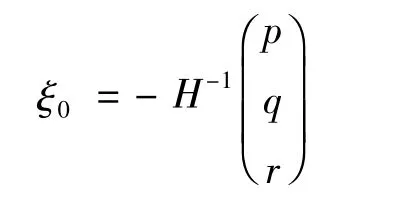
对比误差补偿系数分解模型可得:
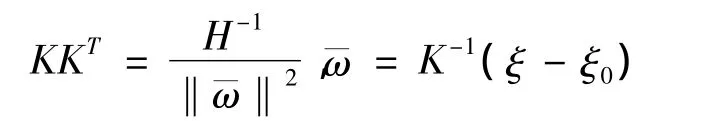
由此,K-1即为本方法获取的误差补偿系数矩阵,即

通过补偿后可消除零偏ξ0、正交性误差和灵敏度误差。由上式可得:
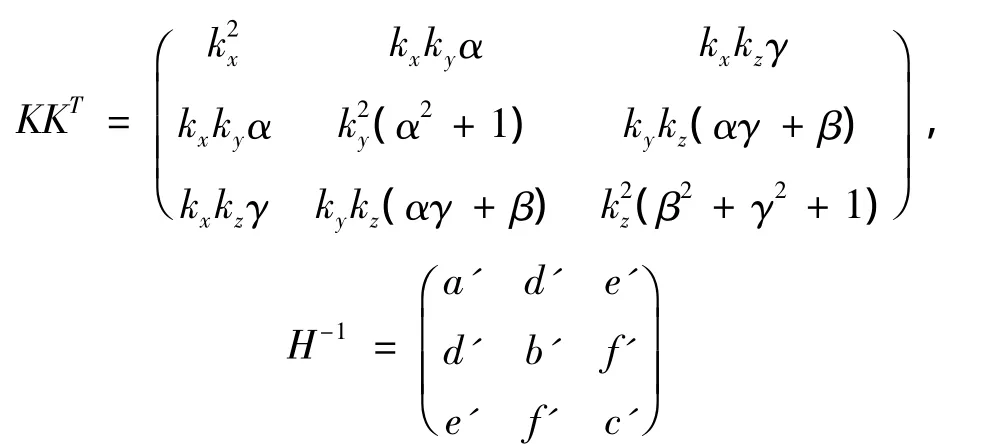
根据不同表达式中的参数关系,经计算可近似得出各系数为:

2.2.2 构造目标函数寻优
构造正确的目标函数,进行多变量函数寻优,是求得矩阵S中对角线以外位置参数的关键。在进行目标函数构造时,需要取具有绝对数值的目标值作为构造函数的依据。对于加速度计,倾角为绝对角度,具有简易可寻找的特点,可由倾角构造目标函数,求解与加速度计相关的剩余参数φ、θ、δ,倾角正切计算公式为

对于磁强计,方位角为绝对角度,具有稳定可寻找的特点,可由方位角构造目标函数计算与磁强计相关的剩余参数。对构造的目标函数寻优,是一个多变量函数无约束寻优问题,求解的方法也有多种,可以使用Matlab内置的函数进行求解,如fminimax函数等。由此,计算出对应系数后即可完成传感器误差补偿:
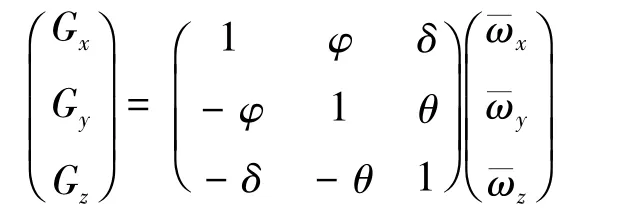
在使用多种算法结合进行参数求解的过程中,对于不同传感器,必须先求解加速度计的校准参数,再求解磁强计的校准参数。
2.2.3 校准流程
根据校准的执行过程,校准流程如图4所示。
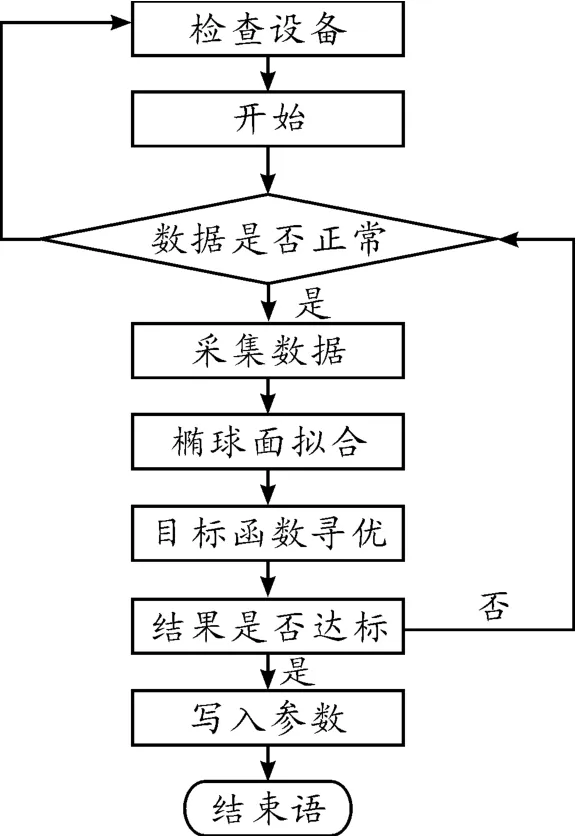
图4 校准流程
3 校准结果
为了检验本文计算方法的有效性,下面给出未校准前、特殊位置法校准、算法计算校准时的倾角和方位角,各角度值如表1所示。其中INC表示水平倾角;GTF表示重力工具面角;AZ表示方位角;所有数值的单位均为度(°)。
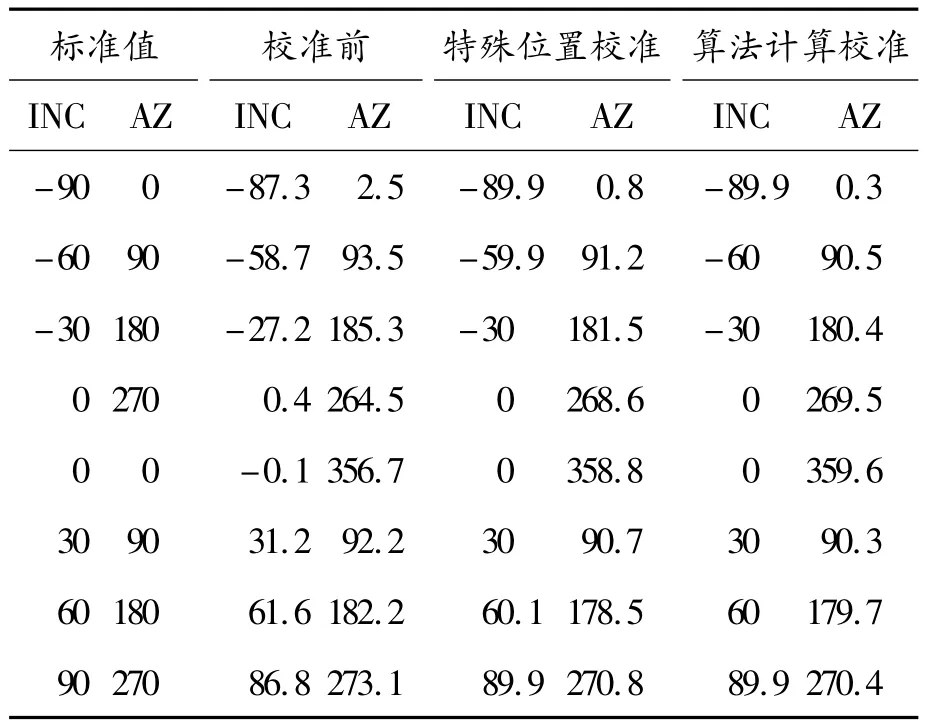
表1 校准前后角度结果比较
使用特殊位置法校准,校准倾角误差小于±0.1°,校准方位角误差小于 ±1.5°;使用软件计算方法校准可以达到此精度要求,校准倾角误差小于 ±0.1°,校准方位角误差小于 ±1.5°。使用软件计算的方法进行测斜仪校准,可以减少对高精度校验设备的依赖。本方法经过继续研究还可以进一步提升校准精度,尤其是方位角的精度。方位角精度的进一步提高能够使水平测斜左右轨迹调整更加准确和及时,使钻孔轨迹测量更加精确,有利于进行高精度钻孔施工和地质测量。
4 现场试验
经过校准的测斜仪在煤矿现场试验中使用良好、运行状态稳定。使用该种测斜仪进行钻进方向调整和钻孔轨迹测量时,轨迹调整准确、及时、方便、信号传输稳定,熟练操作成孔装置后可以较好地控制实钻轨迹与设计轨迹尽可能重合或根据地质条件准确调整实钻轨迹,未出现任何异常。测斜仪现场试验时,某钻孔实钻测量轨迹如图5所示,其中蓝色为设计轨迹,红色为实钻轨迹。根据实钻过程中探测的地质条件进行设计,较好地完成了钻孔施工。
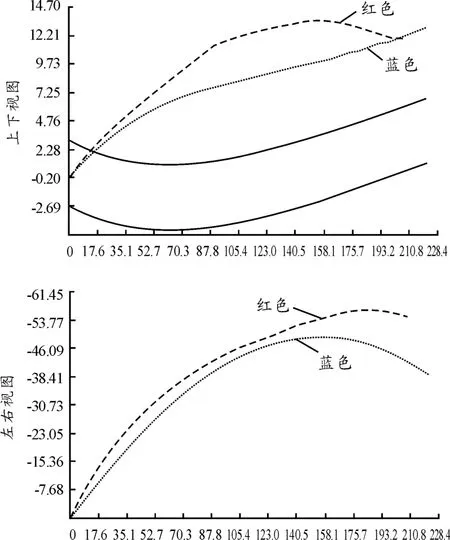
图5 某矿150109回风巷1#钻场3#钻孔测量实钻轨迹图
5 结束语
本文研究使用数学计算的方法求解测斜仪校准参数,将不同类型的误差剥离开来,分别计算不同的误差补偿系数。这种分析求解的方法逐步减小了多种误差复合的综合影响,对各种误差可能造成的影响单独处理,有利于使用软件求解得到各种误差的精确补偿参数,从而提高对测斜仪校准的精度。本院自主研发的煤矿近水平测斜仪通过校准后现场试验,试验结果显示轨迹测量准确,钻孔钻进方向调整及时、正确,测量系统整体运行稳定,可满足高精度钻孔施工、地质测量和特殊钻孔施工要求,适用于煤矿及其他行业定向施工作业。
[1]刘匡晓.随钻测斜系统的数学模型分析及应用[J].石油仪器,1996,10(2):37-39.
[2]徐涛.水平定向钻进随钻测量方法及定位技术研究[D].长沙:国防科学技术大学,2006.
[3]张玉波.随钻测斜仪中传感器信号处理技术研究[J].昆明理工大学学报,2010,35(2):72-75.
[4]温强.双三轴正交测量系配准误差建模与校正研究[J].系统仿真学报,2009,21(5):1274-1277.
[5]王鑫,油井测斜系统数学建模及校准方法研究[J],测井技术,2009,33(2):103-105.
[6]张炜,程锦房.一种三轴磁传感器正交误差校正的简便方法[J].兵工自动化,2009,28(12):75-78.
[7]林春生.三轴磁强计正交误差分析与校正[J].探测与控制学报,2005(6):9-12.
[8]谢子殿,朱秀.基于磁通门与重力加速度传感器的钻井测斜仪[J].传感器技术,2004,23(7):30-32.
[9]宋丽君,秦永元.MEMS加速度计的六位置测试法[J].测控技术,2009,28(7):12-13.
[10]张玉波.随钻测斜仪中传感器补偿及信号处理技术研究[D].大庆:大庆石油学院,2007.
[11]徐涛,温东,孙晓磊.基于加速度计和磁强计的方位测量与校正技术研究[J].仪器仪表学报,2009,30(10):2018-2022.
[12]陈文渊.随钻测量系统信号测量的关键技术研究[D].重庆:重庆大学,2011.
[13]王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2006.
[14]Renk E L,Rizzo M,Collins W.Calibrating a triaxial accelerometer magnetometer using robotic actuation for sensor reorientation during data collection[J].Control Systems,2005,25(6):86-95.
[15]Frosio I.Autocalibration of MEMS accelerometers[J].IEEE transactions on instrumentation and measurement,2009,58(6):1357-1361.
[16]Camps F,Harasse S,Monin A.Numerical calibration for 3-axis accelerometers and magnetometers[C]//IEEE International Conference on Electro/Information Technology.[S.l.]:[s.n.],2009:217-221.
