灰色系统理论在汽车工程中的应用与分析

赵振东

(无锡同捷汽车设计有限公司，江苏无锡 214072)

灰色系统理论在汽车工程中的应用与分析

赵振东

(无锡同捷汽车设计有限公司，江苏无锡 214072)

介绍了灰色系统理论的基本特点和主要内容，分析了灰色理论在汽车工程领域应用的可行性及应用现状。介绍了灰色关联分析、灰色建模与预测的理论方法，并通过实例展示了灰色理论在汽车设计中的方案选择、数列预测、多目标优化等方面的有效应用。

灰色系统理论;汽车工程;复杂巨系统

近年来，随着人们对汽车乘坐要求的提高，与之相关的安全、噪音和防公害研究也得到高度重视。数学、力学、计算机科学、人工智能等学科的迅猛发展，为解决汽车工程领域的问题提供了有力的工具。同时，汽车工程领域历来是基础科学理论及技术应用研究的热点，对于来自轨道车辆、航空、航天、机械工程等领域的新兴技术和方法极为敏感，众多边缘学科、新兴学科亦在汽车工程领域得到不同程度的探讨与运用。

灰色系统理论于1982年由我国学者邓聚龙教授创立，是以“部分信息已知、部分信息未知的小样本、贫信息”不确定性系统为研究对象的一门系统科学新学科，它主要通过对“部分”已知信息的生成、开发来提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控［1］。由于国内外学者的不懈探索，近年来，灰色系统理论不仅在理论上迅速发展，日臻完善，其应用亦遍及农业、能源、石油、地质、气象等众多领域，成功地解决了生产、生活和科学研究中的大量实际问题［1－2］。灰色系统理论在机械工程领域也得到一定的应用和研究，在设计方案评价、参数优选、试验数据的处理和优化设计等方面均取得了进展［3］。文献［4］运用灰色理论预测了汽车齿轮的疲劳寿命。文献［5］运用灰色系统理论研究了金属钢的蠕变寿命。文献［6］根据灰色理论和应力－强度干涉理论，提出了机械零件可靠性灰色预测方法。文献［7］把灰色建模和灰色关联分析用于机械设备的故障诊断中，较好地解决了设备状态预测和故障模式识别问题。文献［8］采用灰色聚类法评价机械产品质量。

复杂巨系统是指子系统种类繁多、有层次性、关联关系很复杂的系统。如果这个系统又与外界存在能量、物质和信息的交换，那么就是开放的复杂巨系统。由人和车辆构成的系统是典型的开放复杂巨系统。人和车辆之间的关系不仅复杂，而且随时间及情况的变化而变化，具有易变性，可以概括为:系统因素不完全明确，因素关系不完全清楚，系统结构不完全知道，系统的作用原理不完全明了，即该系统为“信息不完全”系统。因此，由人和车辆构成的系统是典型的灰色系统，这是可以应用灰色系统理论对人－车系统进行分析的理论研究［9］。文献［10］利用模糊判断和灰色关联度的方法判断发动机的技术状况。文献［11］利用灰色系统理论中的关联度分析方法对齿轮故障进行分析。但就目前所见，运用灰色系统对汽车工程领域进行应用研究的文献与资料较少，灰色理论在汽车工程领域尚未开展系统性、开创性的研究及应用，该技术方法仅在汽车设计中有局部运用与尝试［12－14］。

1 理论的主要内容及运用

1.1 理论概述

灰色系统是以灰色关联空间为基础的分析体系，是以灰色模型GM为主体的模型体系，也是以灰色过程及其生成空间为基础与内涵的方法体系。它是以系统分析、建模、预测、决策、控制、评估为纲的技术体系［15］，其理论基础是灰朦胧集，方法基础是系统科学与应用数学，实践基础是系统工程应用，哲学基础是马克思主义认识论和实践论［1］。

灰色系统理论主要研究“小样本不确定问题”，它与研究“大样本不确定问题”的概率统计及研究“认知不确定问题”的模糊数学在研究对象、理论基础、处理手段等方面均有明显的区别［1］。灰色理论的主要内容有:因素相互影响的关联分析;建立微分方程模型的灰色建模及预测;灰色决策与灰色控制等［2］。

1.2 关联分析

灰色关联是灰色系统的基本概念，是指事物之间的不确定关联，或系统因子之间、因子对主行为之间的不确定关联。灰色关联分析用来做系统因子与行为的量化与序化，根据系统各因子之间或系统各行为之间发展态势的相似或相异程度，分析和确定因子间的影响程度或因子对主行为的贡献测度［3］。

1.2.1 分析方法

灰色关联分析的具体方法是［3，16］:根据参考数列(评价标准)曲线和被比较数列(设计方案)曲线间的相似程度来判断关联程度，其主要步骤如下:

1)选取评价指标(即确定参考数列)，并确定各评价指标的权值Pk;

2)建立灰色关联模型。

首先，参考数列应选取所有被比较数列中各项指标的最优者。当指标属于“效益型”时，选取所有被比较数列中该项指标的最大值;当指标属于“成本型”时，选取所有被比较数列中该项指标的最小值。

其次，计算关联系数。设有i个被比较方案(被比较数列)，k个比较指标。关联系数r0i(k)是各被比较数列曲线和参考数列曲线在各点的相对差值。计算公式为

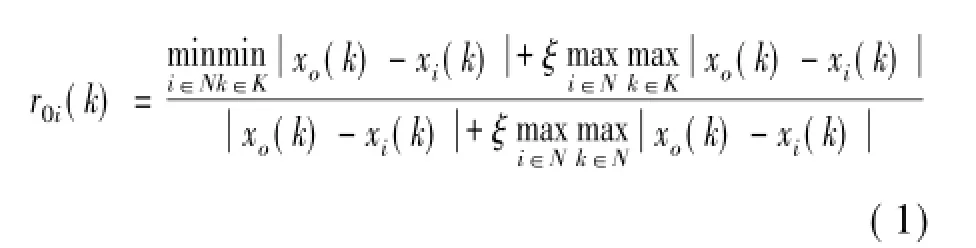
3)计算关联度。

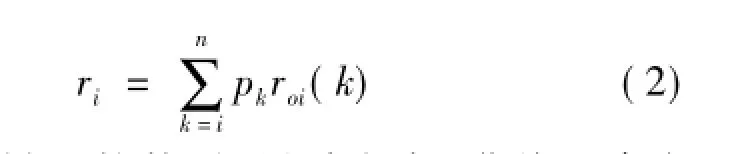
关联度ri可用求加权平均的方法得到，计算公式为ri越大，表示被比较数列(设计方案)曲线和参考数列(评价标准)曲线越接近，即相应的设计方案越优。

1.2.2 基于灰色关联分析的汽车设计载荷基准的确定［14］

在某车型开发中，为确定标杆样车的设计载荷基准，项目组进行了3种不同载荷的12项整车性能主观评价试验，各评价指标得分见表1。试验评分采用10分评分法，10表示驾驶员感觉最佳，分值越低表示感觉越不佳。

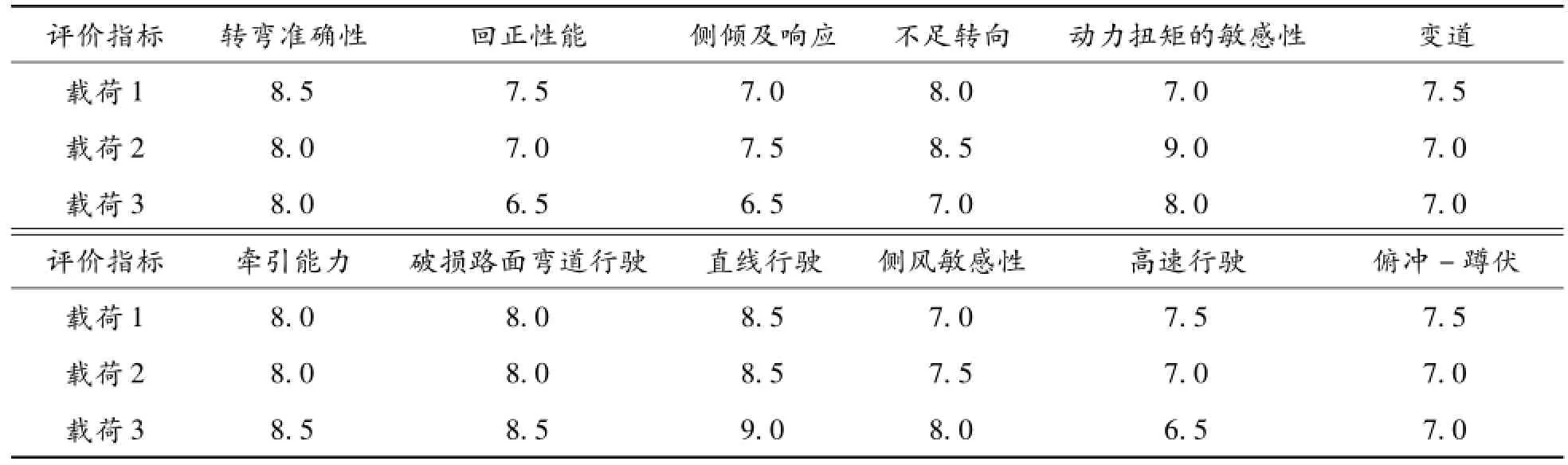
表13 种载荷方案各评价指标得分

由表1可以列出3种被比较数列在3种载荷状态下的数据数列x1，x2，x3。参考数列选取3种待评数列中各项指标的最优者。对上述数列进行均值化处理，由式(1)计算各关联系数:

由式(2)计算得到关联度r1=0.801，r2= 0.861，r3=0.686。其中计算所需各评价指标的权值Pk根据专家意见给出。由关联度r2＞r1＞r3可知，载荷2与参考数列的关联度最大。因此，样车设计载荷基准为方案2。

1.3 灰色建模及预测

1.3.1 数据生成及建模

灰色理论认为，尽管客观系统表象复杂，数据离散，但它总是有整体功能的，总是有序的，总是潜藏着某种内在规律的。灰色系统理论是通过对原始数据的整理来寻找数的规律，称为数的生成。它通过对原始数据的累加达到强化规律性和弱化随机性的目的。累减生成作为累加的逆过程用于信息的还原、增殖及检测等。数据的累加生成在灰色理论中具有独特的地位和作用［17］。

灰色理论用到的模型一般有时间函数形式的时间响应模型、微分方程描述的动态模型、拉普拉斯变换关系描述的线性常系数的系统动态模型［18］。

1.3.2灰色预测

灰色预测是指根据过去及现在已知的或非确知的信息，建立一个从过去引伸到将来的灰色GM模型，从而确定系统未来发展变化的趋势，并为规划决策提供依据［3］。灰色预测模型是灰色系统理论的重要组成部分，一般是指GM(1，1)模型及其扩展形式。它突破了一般建模方法要求大样本数据的局限，是建模思路和方法上的创新［19］。灰色预测方法包括数列预测、灾变预测、拓扑预测与系统预测等［15］。一般等间隔时间序列的灰色预测主要步骤如下［18－19］:

1)给定原始时间数据序列

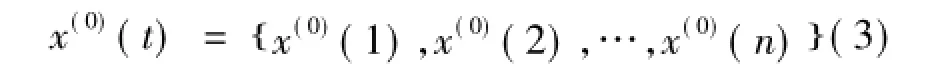
式(11)、(12)中:q(0)(t)为残差;e(t)为相对误差。

1.3.3 汽车橡胶元件蠕变性能的灰色建模及预测

选取某汽车用橡胶元件试样进行蠕变试验，对试样施加恒定载荷，测量一定时间间隔变形S的变化量ΔS值，试验数据如表2所示。

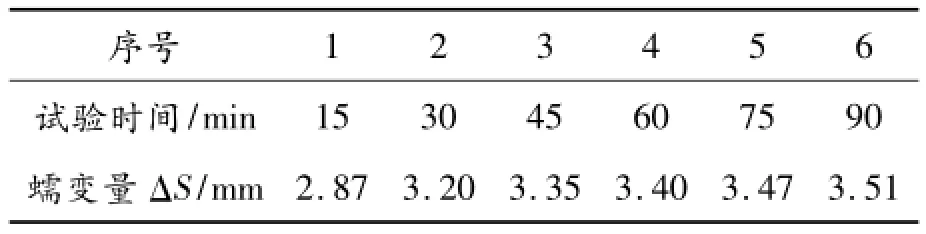
表2 橡胶试样蠕变试验值

本例原始数据中，由于预测蠕变量与时间间隔对应，预测变量为单变量，且模型为一阶模型，因此采用GM(1，1)模型。模型精度与对原始数据的取舍有关。根据信息优先原理，选取2～5号蠕变量数据为原始数据，对上述数据进行初值化处理［16］，得

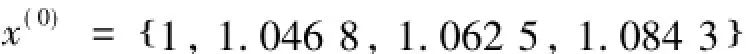
按式(4)进行累加处理，并根据式(5)～(9)得到时间响应方程为

由式(10)进行数据还原，并根据式(11)～(12)进行误差检验，得到结果见表3。

经残差检验，计算的平均相对误差仅为0.12%，证明模型精度较高，可用于预测。由式(13)可知，取k=6时，(1)=5.296 5，还原计算得(0)=3.528 6。对照表2所示数据，计算其相对误差为0.53%，模拟值与试验值吻合较好。

需指出的是，灰建模是少数据建模，用4个数据就可以建立GM(1，1)模型。对于3个数据的情况，则可采用“首位灰序列建模”方法［3］。回归分析、概率统计均需要大样本数据作为分析基础。同时，灰建模所需样本数据允许被噪音污染［3］。

一般来说，灰色GM(1，1)模型用于短期预测，如果需要作长期预测，可以建立新陈代谢GM(1，1)模型，或者运用LGM(1，1)长期预测模型［18］。

表3 模拟结果及误差检验表

1.4 灰色决策

灰色决策是含有灰量的决策，包括灰色局势决策、灰色聚类分析等［18］。

1.4.1 灰色聚类概念

灰色聚类是灰色分析决策的重要组成部分，按聚类对象划分，可以分为灰色关联聚类和灰色白化权函数聚类。灰色关联聚类主要用于同类因素的归并，以使复杂系统简化。灰色白化权函数聚类是建立在灰数的白化函数生产的基础上，它将聚类对象对于不同聚类指标所拥有的白化数按几个灰类进行归纳，以判断该聚类对象属于哪一类，从而区别对待［3，20］。

1.4.2 灰色聚类方法

记R为关联度集，Rg为聚类对象的相似关系集。算法具体步骤如下［20－21］:

1)求灰色关联度。按式(1)和(2)计算ri，从而得到关联度集R=(r1，r2，…，rm)。R是聚类分析的基础。

2)求相似关系矩阵Rg。根据关联度集R定义评价对象各参数之间的差异矩阵ES为

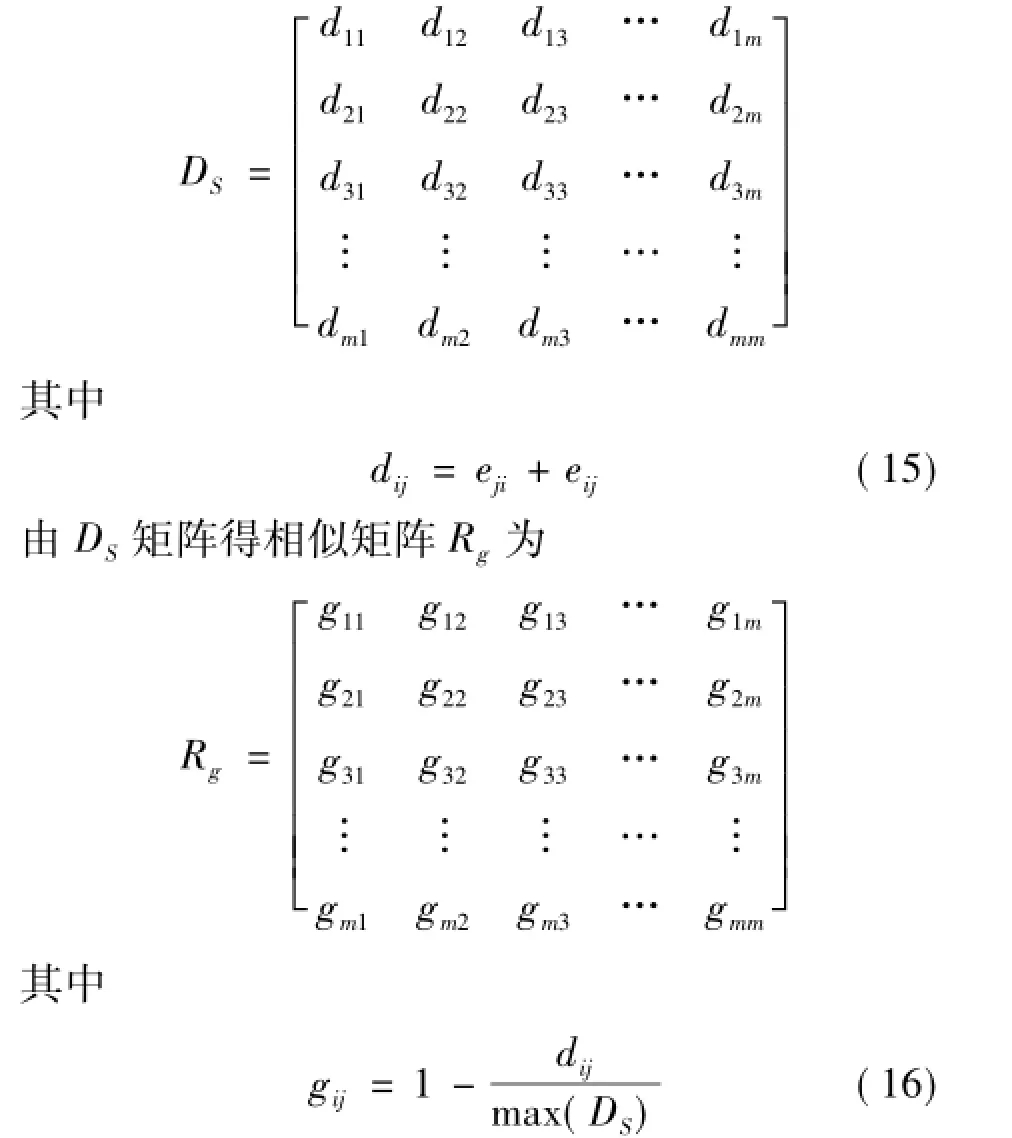
式(16)中max(DS)为DS矩阵中的最大值元素。

3)进行聚类分析。由于相似矩阵Rg反映了被评价对象之间的亲疏关系，因此可用Rg直接评价。

1.4.3 运用灰色聚类法对汽车传动系统进行多目标选型优化

汽车传动系统的选型优化属于较为复杂的多目标优化问题。普通的优化算法只能表达极大或极小，难以对合适或适中等相对模糊的指标进行判断，同时难以给出不同欲望水平下的各方案的优劣赋权序。运用灰色聚类法进行传动系各方案的多目标寻优分析能排出满意解的优劣次序，满意程度可由欲望水平确定，为决策提供了更贴近实际的方法和依据［13］。

表4为8种汽车传动系统的组合方案。对每一种组合均进行性能计算，选取6项性能指标进行分析。表4给出了由专家经验判断的各指标的权值，同时分别定义了各指标的理想属性(指极大↑、极小↓或者适中)及理想值。

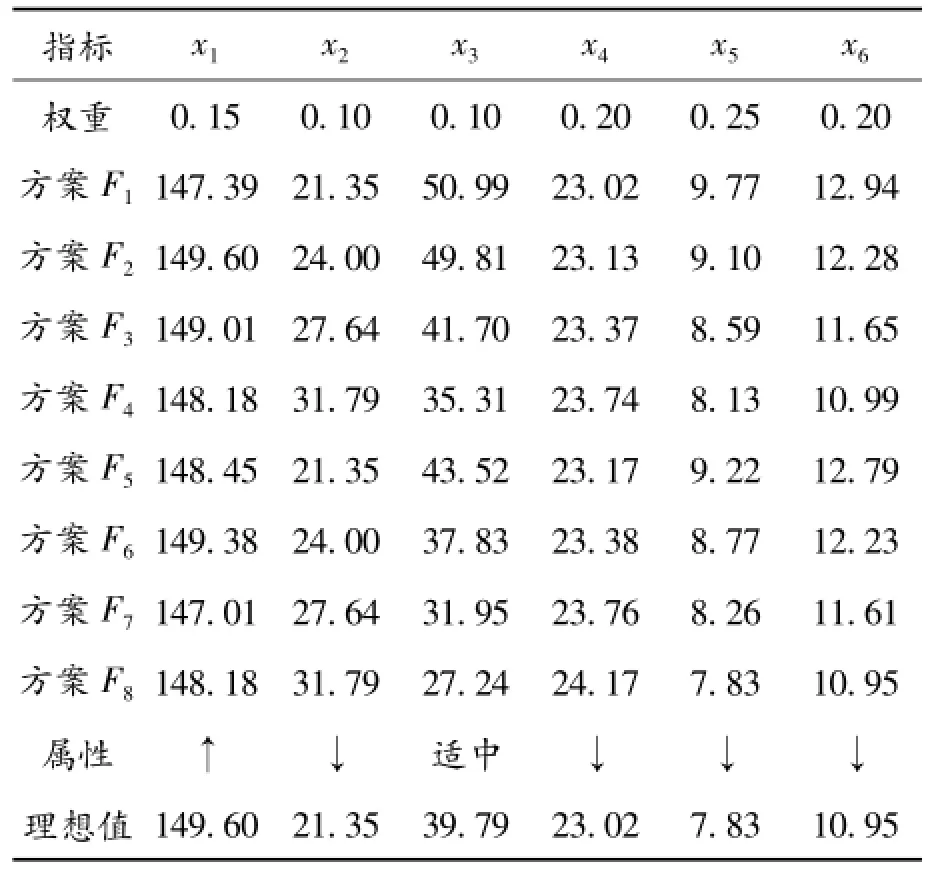
表4 原始数据及属性列表

表4中的x1～x6分别表示最高车速(km/h)、4挡最低稳定车速(km/h)、最大爬坡度(%)、起步连续换挡加速行驶到400 m时的时间(s)、6工况燃料消耗量(L/100 km)、超速挡等速百公里油耗(L)。

由式(1)～(2)和(14)～(16)求得相似矩阵Rg为

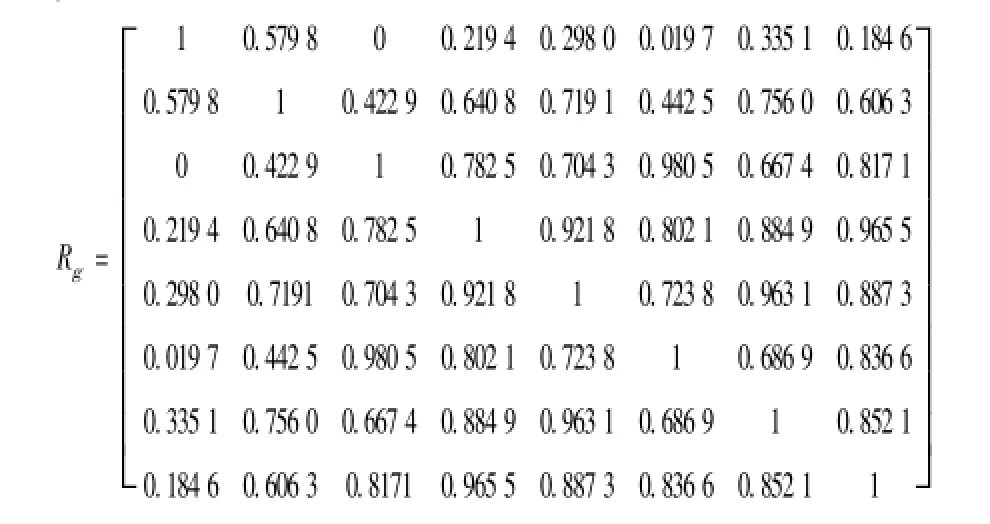
根据相似矩阵Rg，任取实数据λ∈[0，1]，砍断权小于λ的枝，就构成了在λ水平上的聚类。全体水平上分类的集合构成了灰色系统聚类图(图1)。

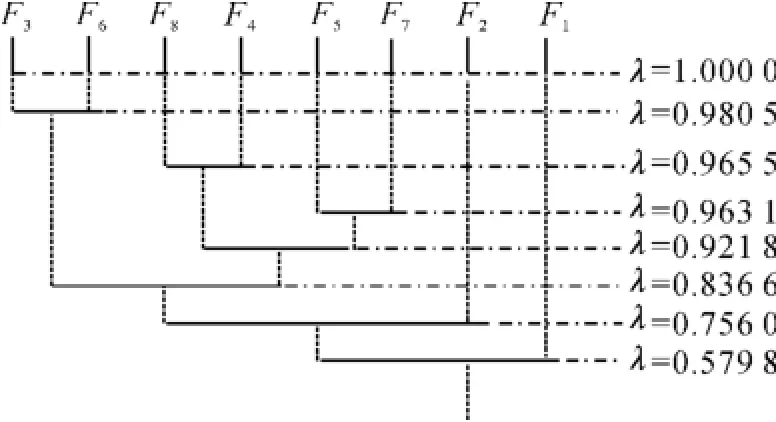
图1 灰色聚类图

1.5 灰色控制

灰色系统控制根据未来系统状态的预测值来制定控制决策是一种事前控制。灰色控制是以GM(1，1)为主体的控制，通过灰色控制可以预测系统行为的发展变化，根据系统行为得到的发展变化对其进行预控制，从而提高控制的准确性与实时性［3，18］。

2 结束语

迄今为止，国内依然是灰色系统理论研究及运用的主要场所，为灰色理论建立、发展、完善和推广做出了重要贡献。鉴于灰色系统理论学科特点，考虑到人－车系统是开放的复杂巨系统，可以用灰色系统理论描述这些多变、难以量化的因素。本文通过理论分析及示例论证了这种运用的可行性。目前灰色系统理论在汽车技术领域的应用研究处于起步阶段，是一个很有发展潜力的领域，有待广大科研工作者的不断深入探讨。

［1］肖新平，毛树华.灰预测与决策方法［M］.北京:科学出版社，2013:1－7.

［2］陈新军.灰色系统理论在渔业科学中的应用［M］.北京:中国农业出版社，2003:1－7.

［3］罗佑新，张龙庭，李敏.灰色系统理论及其在机械工程中的应用［M］.长沙:国防科技大学出版社，2001:1－17，62－84.

［4］于雷.灰色系统理论在汽车齿轮寿命预测中的应用［J］.汽车技术，2006(9):24－26.

［5］翟已.一种预测疲劳及蠕变寿命的新方法［J］.西南交通大学学报，1992(6):42－46.

［6］马春翔.机械零件可靠性灰色预测［J］.机械设计，1989(3):9－12.

［7］段志善，闻邦椿.灰色系统理论在设备故障诊断中的应用［J］.东北工学院学报，1990，11(4):383－389.

［8］罗佑新.用灰色聚类法评价工程机械产品质量［J］.工程机械，1992(12):34－36.

［9］颜声远.武器装备人机工程［M］.哈尔滨:哈尔滨工业大学出版社，2009:344－359.

［10］郝强.发动机技术状况的模糊关联度判断［J］.兵工学报，1990(2):8－13.

［11］吕仲军.应用灰色系统理论诊断变速箱故障［J］.石家庄铁道学院学报，1993，6(3):59－65.

［12］赵振东，邹小俊.汽车风噪声主观评价的灰色聚类分析［J］.机械科学与技术，2011，30(12):2157－2164.

［13］赵振东.灰色聚类法在汽车传动系选型优化中的应用［J］.机械设计与研究，2011，27(3):52－55.

［14］赵振东.灰色关联分析在汽车主观评价数据处理中的应用［J］.汽车科技，2010(6):60－63.

［15］邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1990.

［16］吴顺祥.灰色粗糙集模型及其应用［M］.北京:科学出版社，2009:19－49.

［17］刘永宏.灰色预测模型在机械设备运行状态趋势分析中的应用［J］.江南大学学报，1993:50－59.

［18］袁嘉祖.灰色系统理论及其应用［M］.北京:科学出版社，1991:50－51，100－104，121－128.

［19］党耀国，刘思峰，王正新，等.灰色预测与决策模型研究［M］.北京:科学出版社，2009:1－15.

［20］刘思峰，郭天榜，党耀国，等.灰色系统理论及其应用［M］.北京:科学出版社，1999:42，78－90.

［21］宋俐，魏锋涛，石坤.基于灰色聚类法的蜗杆传动多目标优化设计［J］.机械科学与技术，2007，26(7):885－888.

(责任编辑 杨黎丽)

Analysis and Application of Grey System Theory in Automotive Engineering Fields

ZHAO Zhen－dong
(Wuxi Tongjie Auto－design Co.Ltd.，Wuxi 214072，China)

The paper introduces fundamental feature and main contents of Grey System Theory，and analyzes the feasibility and application status of applying Grey System Theory in automotive engineering fields.The paper emphatically introduces the technology of grey relative analysis and grey model and grey prediction.The instance shows the effective results of applying Grey System Theory in automotive design，reference to resolution selection，prediction，multi－objective optimism etc.Finally，the analysis and application of Grey System Theory in automotive engineering fields should be further studied.

grey system theory;automotive;analysis;complex giant system

U461.99

A

1674－8425(2014)03－0010－07

10.3969/j.issn.1674－8425(z).2014.03.003

2013－11－07

赵振东(1974—)，男，江苏靖江人，博士，高级工程师，主要从事汽车整车开发和悬架设计研究。

赵振东.灰色系统理论在汽车工程中的应用与分析［J］.重庆理工大学学报:自然科学版，2014(3):10－16.

format:ZHAO Zhen－dong.Analysis and Application of Grey System Theory in Automotive Engineering Fields［J］.Journal of Chongqing University of Technology:Natural Science，2014(3):10－16.