一种基于非抽样contourlet变换的图像增强方法

李 诚，骆 且，杜宇人

（扬州大学信息工程学院，江苏 扬州225127）

为了保证橡胶形变检测的精度，前期须对图像进行增强处理．传统的图像增强算法如直方图均衡算法［1］、高斯滤波［2］，小波变换［3－4］、基于contourlet变换［5］等缺乏平移不变性，会产生吉布斯失真，且其中小波变换只能对各向同性图像有较好的增强效果，而对于边缘较多或线性特征的图像增强效果并不理想．非抽样contourlet变换［6－7］由于引入了方向滤波器组而具有多方向选择性，能够有效地抑制噪声．对于橡胶图像而言，有效区分目标和背景的亮度可以达到图像增强的目的，针对这一特殊性，如采用RGB模型进行图像增强则难以控制其色调信息，而HSV 模型能体现人的主观视觉，同时便于计算机进行图像处理；因此，本文在传统图像增强方法的基础上，提出一种非抽样contourlet变换和HSV 模型相结合的图像增强方法．

1 非抽样contourlet变换

图1 NSCT分解结构示意图Fig．1 The nonsubsampled contourlet transform

Contourlet变换中的拉普拉斯金字塔和方向滤波器组虽然能够上下采样，但不具有平移不变性，还会导致吉布斯现象［8］，然而在此基础上改进得到的非抽样contourlet 变换

（nonsubsampled contourlet transform，NSCT）则具有平移不变性，能够有效地抑制噪声，其分解结构如图1所示．由 图1可见，图像的能量主要集中在低频分量中，噪声和细节信息集中在高频分量中，因此对图像的V 分量采用NSCT 分解后的系数进行处理可以有效提高其对比度．

2 本文改进的算法

2．1 HSV模型

HSV 模型由色度（H）、饱和度（S）和亮度（V）3个分量组成［9］．HSV 模型的优点在于消除了V 分量与颜色信息的联系，同时H 分量和S 分量可由人眼视觉系统中的锥状细胞分辨出．图2为橡胶实验图像的HSV 分解结果．

图2 橡胶图像的HSV分解Fig．2 The decomposition of rubber image in the model of HSV

2．2 基于NSCT的图像增强改进算法

人眼视觉特性一般由复合模型、高斯模型、指数模型和Barten模型［10］表征，Barten模型中人眼的调制传递函数（modulation transfer function，MTF）表示为

其中a＝440（1＋0．7／L）－0．2，b＝0．3（1＋100／L）0．15，c＝0．06，f 为频率，L 为显示屏的平均亮度，本文取L＝200cd·m－2．对V 分量作非抽样变换并针对亮度信息加以调整，对系数采用Barten模型进行滤波处理．将S 分量进行非线性变换，因S 分量较暗，故采用对数变换拉伸低灰度区，增强人眼的视觉效果，最后将结果返回到RGB彩色空间．对数变换后图像S 分量为

本文取k＝1．

设（r，g，b）是颜色的红、绿、蓝坐标，r，g，b取值范围都是［0，255］；h为色调角，h∈［0，360°）；s，v为饱和度和亮度，s，v∈［0，1］．在RGB颜色空间中的一点（r，g，b）可以通过式（3）～（5）转换成相应的HSV 坐标（h，s，v）：

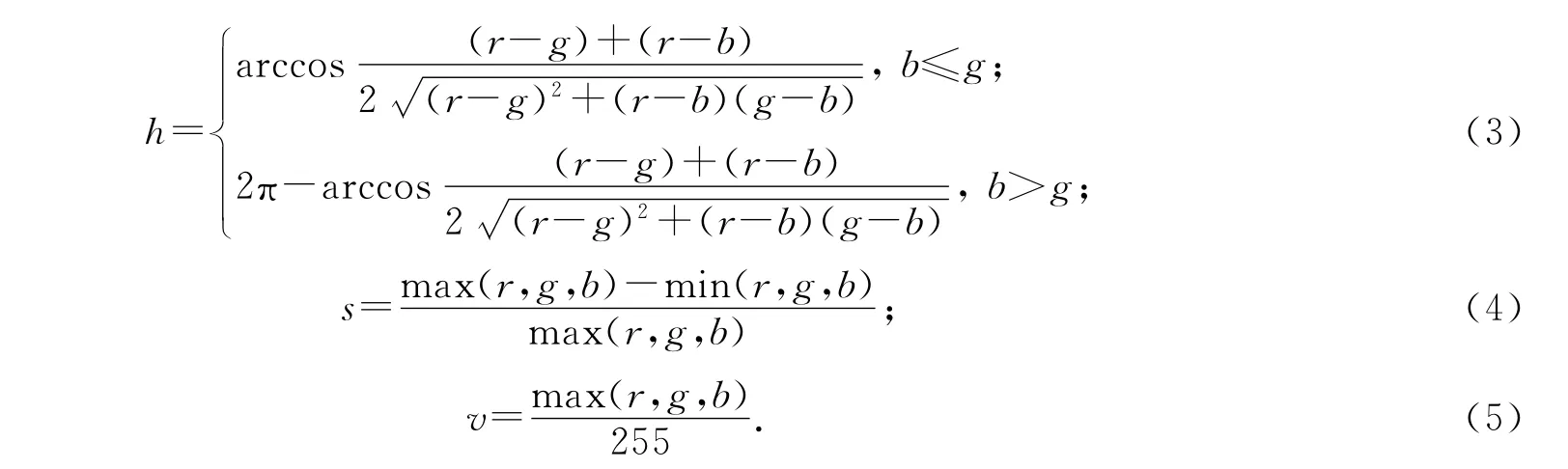
颜色空间从HSV 到RGB的转换可由式（6）～（11）实现：

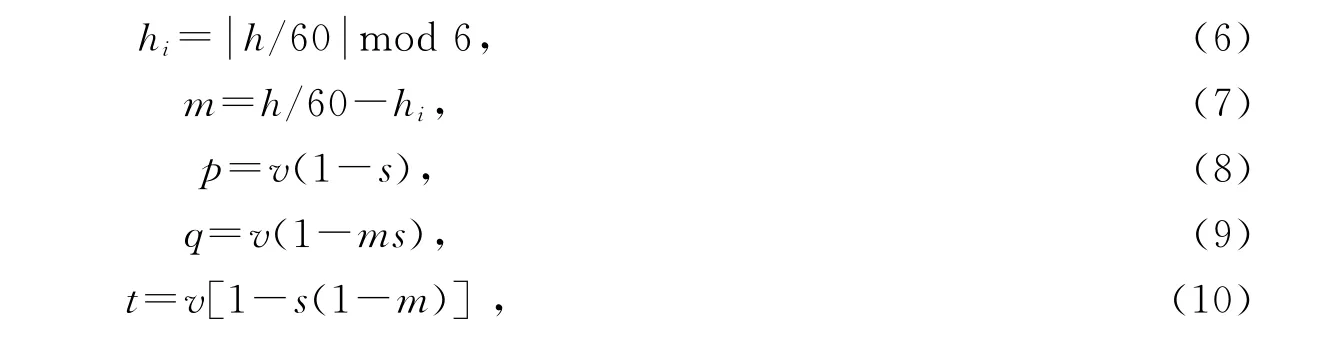
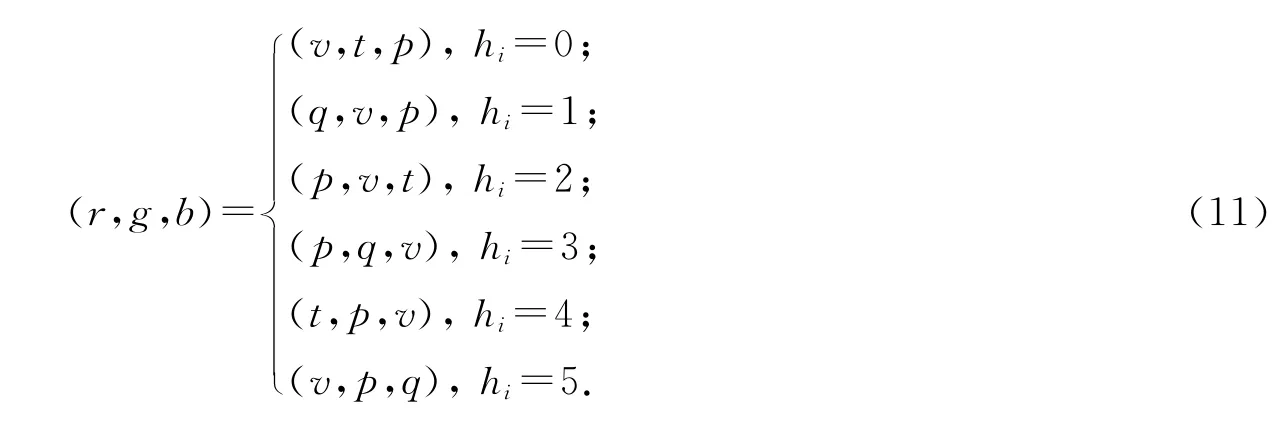
本文算法步骤如下：

1）利用转换公式（3）～（5）将原始图像从RGB空间转换到HSV 空间；

2）对V 分量作非抽样contourlet变换，根据式（1）处理低频系数和高频系数，在频率域达到增强细节、改善图像亮度动态范围的效果，然后重建V 分量；

3）利用式（2）对S 分量进行非线性变换；

4）对S 分量和V 分量作归一化处理，取值区间确定为［0，1］，最后利用转换公式（6）～（11）将增强的图像从HSV 空间转换回RGB空间．

3 结果与分析

对240×400像素的杯盖图像和2组2 848×2 136像素的橡胶图像分别采用小波变换、直方图均衡化和本文算法进行实验对比分析，结果如图3～4所示．

图3 杯盖图像的3种增强算法效果对比Fig．3 The comparison of three kinds of enhancement algorithms with bowl cover

图4 橡胶图像的3种算法增强效果对比Fig．4 The comparison of three kinds of enhancement algorithms with rubber

同时引入信噪比Rsn［11］进行定量评价：

实验结果表明：本文算法的对比度、亮度和饱和度均高于小波变换和直方图均衡化算法，图像的纹理和边缘更加清晰，视觉效果好，去噪性能强．

表1 3种增强算法的信噪比Tab．1 The signal－to－noise ratio of various algorithm

［1］ CHENG H D，SHI X J．A simple and effective histogram equalization approach to image enhancement［J］．Digital Signal Process，2004，14（2）：158－170．

［2］ KNÄUSL B，RAUSCH I F，BERGMANN H，et al．Influence of PET reconstruction parameters on the TrueX algorithm：a combined phantom and patient study［J］．Nuklearmedizin，2013，52（1）：28－35．

［3］ PATIDAR S，PACHORI R B．Segmentation of cardiac sound signals by removing murmurs using constrained tunable－Q wavelet transform［J］．Biomed Signal Process Control，2013，8（6）：559－567．

［4］ VAFAEI M，ADNAN A B．Seismic damage detection of tall airport traffic control towers using wavelet analysis［J］．Struct Infrastruct Eng，2014，10（1）：106－127．

［5］ LIU Gang，LIU Jing，WANG Quan，et al．The translation invariant wavelet－based contourlet transform for image denoising［J］．J Multimedia，2012，7（3）：254－261．

［6］ YUE Chunyu，JIANG Wanshou．SAR image denoising in nonsubsampled contourlet transform domain based on maximum a posteriori and non－local constraint［J］．Remote Sens Lett，2013，4（3）：270－278．

［7］ RODRIGUEZ－SÁNCHEZ R，GARCÍA J A，FDEZ－VALDIVIA J．Image inpainting with nonsubsampled contourlet transform［J］．Pattern Recognit Lett，2013，34（13）：1508－1518．

［8］ 李艳，杜宇人，沈鑫．基于非抽样contourlet变换的图像增强方法［J］．扬州大学学报：自然科学版，2011，14（4）：47－51．

［9］ 吴震宇，杜宇人，师文，等．一种基于模糊熵的水凝胶图像分割算法［J］．扬州大学学报：自然科学版，2010，13（2）：65－69．

［10］ 周燕，金伟其．人眼视觉的传递特性及模型［J］．光学技术：2002，28（1）：57－59，62．

［11］ REDLER G，EPEL B，HALPERN H J．Principal component analysis enhances SNR for dynamic electron paramagnetic resonance oxygen imaging of cycling hypoxia in vivo［J］．Magn Reson Med，2014，71（1）：440－450．