或有现金流的风险探讨

■王少豪

未来的现金流可分为确定的现金流和不确定的现金流，确定现金流又可分为稳定现金流和波动现金流，而不确定的现金流主要为或有现金流。我们在采用收益法进行价值评估的时候大多是对确定的稳定现金流或波动现金流折现，可采用戈登模型或CAPM模型来估算折现率以评估企业或资产的价值。但是当出现或有现金流的时候，情况就会比较复杂。或有现金流的风险往往会大于确定现金流的风险，所以对于不确定的现金流由未来期望值折现求出现值则不是那么容易的事情。我们可以从下面几个案例初见端倪。

一、通过或有补偿案例看或有现金流风险

如果某企业目前有两千万的自由现金流，而且预计会以每年15%的增长率增长五年，之后趋于稳定。在那个时候，公司价值将是自由现金流的八倍。所要求的回报率（WACC）由公司的系统风险所决定，为12.5%。评估出来的公司价值是28545万元，这就是一般情况下运用收益法评估企业价值的过程。具体计算如表1所示：

表1 金额：万元

现在，我们来研究第一年的现金流：第一年现金流价值是2300万元，折现值是2044万元。但这个现金流如果不是一个完全的确定现金流，而是由稳定的现金流和一个不确定的现金流组合而成，即如果第一年公司自有现金流达到1053万元以上，则有一个基于超额部分的补偿。那么这个超额部分是不确定的，我们认为超额部分现金流的期望值是1247万元，两者加起来为2300万元。因此这个2300万元只是一个概率分布的期望值，并假设其遵从正态分布。那么可以通过表2来表现用概率分布显示的第一年现金流的情况。

表2 金额：万元

由于我们不能总是给未来现金流的分布建造一个明确的模型，所以在使用预期价值的时候，这样的分布总是隐晦而不清晰的。因此，估算或有补偿现金流的预期价值及其概率分布是评估或有补偿价值中最为关键的两步骤之一。

或有现金流的产生源于并购或其他经济活动中产生一个或有补偿的协议，比如说对赌协议。典型的情况是给或有补偿定义一个门槛，即企业的现金流高于1053万元时，给出的补偿是超出部分现金流的10%或50%，总之是以高出门槛值部分为基础的。那么高出1053万元的现金流的期望价值为1247万，如表2所示。但最后其折现为当前公平市场价值会是多少就不得而知了，因为不知道折现率。

评估师可能会暂且认为公司现金流和或有补偿的现金流区别不大，而用公司的WACC=12.5%作为折现率。但事实上，两者的折现率是完全不同的。下面我们利用表2的数据演示这一现象，并找到问题的答案。

如表2所构造的那样，现金流的分布从1053到4580有不同的概率，而其分布与概率的乘积加和等于第一年的现金流2300万元。然后我们把这个总的现金流分成两部分：第一部分是常数，即无风险的部分，其值为1053万元，相当于概率分布最小端的值；第二部分则是总现金流减去无风险部分的剩余值。由于把现金流分成了两部分，所以就不能用总现金流的回报率作为风险部分现金流的折现率了，而应该推导出风险现金流适合的折现率。

或有补偿现金流是风险部分现金流的百分比（10%或50%）。我们知道，总现金流的折现值是2044万元，同时又知道用无风险利率2%去折现无风险部分现金流1053万元得出价值1032万元。因此，我们把2044减去1032就得出风险部分现金流的折现价值，即为1012万元，并由此得出这部分现金流所要求的回报率，也就是折现率。本例中，无风险利率是2%，无风险现金流的折现价值为1032万元。所以风险现金流部分的折现率应该是23.2%，即1247/1012－1=23.2%。

可见这部分现金流的风险是总现金流的1.856倍(23.2/12.5=1.856)。不过，这个答案也只能是针对表2的这种特殊情况，因为这里的现金流只分为无风险现金流与或有现金流。而对于大部分与市场相关的或有补偿来说，要区别出这部分系统风险以及求出评估价值所需的折现率有很大的挑战性。

由于第二部分现金流是总现金流的比例派生物，所以我们也可以通过采用MM理论的研究成果来证明这一结果的正确。MM理论推导出在具有无风险债务的资本结构中权益所需回报率与权益本身之间的关系，即权益所需的回报率取决于公司资产所需的回报率、无风险利率以及公司的负债权益比。在我们的案例中，总现金流对应于资产的回报率；固定的现金流部分1053万的元，我们称之为第一部分对应于债务的回报率，其折现价值等于1032万元；第二部分现金流即高于1053万元的部分就是权益的回报，其折现值为1012万元。在MM理论推导的方程中设定：权益的回报率为rE；资产的回报率为rA；无风险利率为rf；债务权益比为D/E。则有：

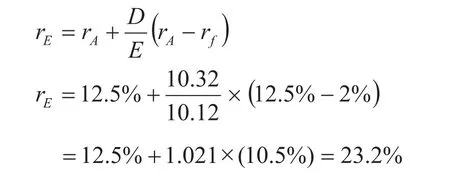
如上所示，我们用两种方法求出所需的回报率，但这只适合于本案例的简单情况：即把现金流分成两部分，无风险的现金流（债务）和风险现金流（权益）。但是在实践中，大部分或有补偿产生的或有现金流的情况要复杂的多，不可能简单地分为无风险和有风险的现金流，因此也就无法像上述所示求出或有现金流的折现率。因为那个时候一般有三种以上的现金流，因而也就有三个以上的未知折现率，上述方法因此而无能为力。也正因为如此，收益法在具有期权性质的或有现金流的情况下也多半是无能为力的。所以这才产生了期权定价的评估方法，因为或有现金流可以被看做一个期权。

二、期权风险与股票风险的比较

由于或有现金流可以被看做一个期权，所以我们可以通过二叉树期权定价方法来推导，期权的风险比股票或其他证券市场上交易的有价证券的风险大得多，从而也看出或有现金流的风险要大于确定现金流的风险。具体推导过程如下：

考虑一个价格为S0的股票，基于该股票的某个期权的当前价格为f，期权的有效期限为T，当到时刻T期权价格或者从S0上升到S0u，或从S0下降到S0d。这里u=(S0u/ S0)＞1，d=(S0d/ S0)＜1。当股票价格上升到S0u，价格的增长比率为u－1，当股票价格下降到S0d，价格的减少比率为1－d。假设在股票价格上升或下降的两个时点，期权的内在价值分别为fu和fd，如下图1所示：

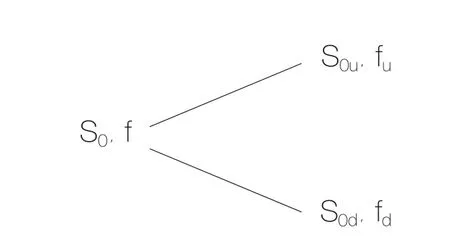
图1 股票期权组合上升下降图

为推导出期权价值，我们需要构建一个股票和期权的无风险组合。此处我们构建的是由n股的股票多头和一个期权空头的无风险组合。当股票价格上升时，期权期末组合价值为：如果股票价格下降，组合价值为：由于是无风险状况，所以两者的价值相等，即：

由此可以推导出n的数量：

在这种情况下，该组合是无风险的，因为无论股价如何变化其组合的价值不变。而这个时候的持股数量n就是期权价值变化与股票价格变化之比。此时组合的收益率也一定是无风险利率，如果用r来表示无风险利率，则组合的现值为而最初构建该组合的成本是：所以两者相等，即：

移项并用u=S0u /S0代入得：

把公式(1)中的n代入上式，则可以得出：

其中：

以上就是单步二项树法求取期权价值的公式。

上式中，u=(S0u / S0)＞1；d=(S0d / S0)＜1；P可以称之为假概率。

这时，我们可以引入数字的案例，以便更清楚地看到推导的过程和结果。假设对投资者而言没有任何套利的机会，我们可以以某种方式构造一个股票和基于该股票的期权的组合，使得在三个月后该组合的价值是确定的。这个组合就是包含一个n股股票多头和一个股票看涨期权的空头。假设股票当前的价值是20元，3个月后的价格可能是22元或18元。而该股票期权是三个月后以21元的价格买入该种股票的欧式看涨期权。于是：Sou=22 ；S0=20；u=1.1；Sod=18，S0=20；d=0.9；fu=1；fd=0；T=3/12=0.25；设无风险利率r为12%，则有：

从而可以求出该股票期权的价值为：

由公式2可以看出参数p是一个很重要的变量，我们把它称之为假概率，实际上它就是在假设的风险中性世界里股票价格上升的概率。所谓风险中性世界定义为所有人对于风险的认识都是无差异的世界，也就是说在这个世界里，投资者对风险不要求补偿，所有证券的预期收益率都是无风险利率。在公式2中可以很明显看出，期权的当前价值就是期权在期末的预期收益再经无风险利率折现。同样，我们也可以推导出在风险中性世界的假设前提下，股票价格的增长也是以无风险利率增长的，即

这就是期权估值中一个很重要的风险中性估值原理。它是当期权估值时，假设世界是风险中性的，这样我们得到的期权价值不仅在风险中性世界里是正确的，在其他世界中也是正确的。

但是，必须强调的一点是，p是一个在风险中性世界里股价上升的概率，此时股票和期权的预期收益率均为无风险利率，如案例中的12%。而在现实世界中事实并不会这样，如现实世界中股票的预期收益率可能会是16%，那么此时股票上升的概率将会是多少？

根据上面公式可以求出：因此现实世界中期权的预期收益就是：

但是在现实世界中，我们无法确定适用于该项期权预期收益的准确折现率，因而也就无法求出期权的当前价值。这也是我们为什么要在期权估值中应用风险中性估值原理的原因。因为现实中，持有看涨期权头寸比持有相应股票头寸的风险更大，所以对该期权预期收益折现的折现率肯定要大于股票的预期收益率16%。到底大多少？在不知道期权当前价值的情况下不得而知。

这时，我们想起前面用风险中性估值原理求出来的期权当前价值是0.633，所以可以代入折现的公式：得出：这就是现实世界中，当股票的预期收益率为16%时，股票期权的预期收益率。也就是说，在这个案例中如果要给期权的预期收益折现的话，这个折现率k应该是42.58%，是股票预期收益折现率16%的2.675倍。

三、结论

从上述两个方面的案例演示可以得出以下结论：

1. 或有现金流的风险要大于确定现金流的风险；期权的风险要大于该期权所依附的股票的风险。无论是或有补偿案例还是二叉树期权定价公式的案例都可以看出：两者的风险（预期收益率）是不相同的，而且明显前者要大于后者。所以，评估师在遇到有或有现金流的时候，或是有类似期权的时候，一定不能只考虑确定现金流的风险，而忽视或有现金流的不同风险。

2. 虽然知道或有现金流的风险不同于确定现金流的风险，但是如何求出这个风险却是一个难题。这也就是为什么收益法在遇到期权性质的资产或收益的时候，不能发挥作用的原因。本文的两个案例中均是采用其他手段先求取或有现金流或股票期权的准确价值，而后倒推出它们的预期收益率。特别是第一个或有补偿的案例，是一个特殊情况，即总现金流只分为门槛现金流和补偿现金流两部分时，可以通过知晓总现金流的WACC和门槛现金流的无风险利率，倒推出或有现金流的折现率。但绝大部分或有补偿的情况都是三部分以上的现金流，这时两个以上的未知折现率将是无法得出的。因此此时，我们将无法采用收益法，而只能运用期权定价的理论来求取或有现金流或期权的当前价值了。

[1]翰·赫尔. 期权、期货及其他衍生产品(第六版).人民邮电出版社，2009.

[2]理查德·布雷利，斯图尔特·迈尔斯.资本投资与估值.中国人民大学出版社，2010.

《春上枝头》 周东