PDC切削齿与岩石相互作用模型

王家骏,邹德永,杨 光,何仁清,陈修平

(中国石油大学石油工程学院,山东青岛 266580)

PDC切削齿与岩石相互作用模型

王家骏,邹德永,杨 光,何仁清,陈修平

(中国石油大学石油工程学院,山东青岛 266580)

使用可以加载钻压的试验设备,在不同钻压、切削面积、切削速度和切削齿后倾角条件下对不同性质的岩石进行钻进试验,通过对试验数据的多元非线性回归分析,建立新的PDC切削齿与岩石相互作用模型。结果表明:切削面积是影响切削齿受力的主要因素;切削齿受力随切削面积、切削齿后倾角和岩石可钻性级值的增大而增大;切削齿受力与切削速度呈对数关系。

PDC钻头;切削齿;相互作用模型;钻速;钻压

PDC切削齿与岩石相互作用关系对预测钻速十分重要。前人在车床上做了PDC切削齿切削岩石试验[1-2],建立了PDC切削齿与岩石相互作用模型。以往的试验设备是车床,在切削岩石的过程中不能给钻头加载钻压,只能在固定切削深度条件下测得切削齿受力,实际钻井时切削齿在钻压下切削岩石,因此这些试验不符合实际情况;当钻头转速不同时,同一切削齿的切削速度不同,这对切削齿受力有很大影响,以往的试验没有考虑这一因素;前人使用逐步回归法对试验数据进行分析,模型的预测结果与试验数据误差较大。针对以上问题,笔者使用可以加载钻压的试验设备,在不同切削速度下进行试验,并用多元非线性回归方法对试验数据进行分析。

1 PDC切削齿切削岩石试验

1.1 试验装置

试验装置为中国石油大学(华东)的XY-2B型钻机(图1(a)),钻机由调速电机、方钻杆、钻头、加压装置、传感器和数据采集系统组成。试验用钻头由3个切削齿构成,如图1(b)所示。

1.2 试验原理及方法

钻机由调速电机产生转速和扭矩,方钻杆带动钻头旋转,轴向加压装置给予钻头钻压,传感器和数据采集系统可以实时收集钻压、扭矩和位移的信息,通过这些信息可以测定切削齿的正压力Fn和切削力Fc。用PDC微钻头在华石Ⅰ型岩石可钻性测试仪上测定岩石可钻性级值,用硬度计测定压入硬度,用三轴应力仪测定岩石的抗压强度和抗拉强度,表1中为岩石参数的平均值。在不同的切削齿直径、后倾角、钻压和切削速度下进行试验,试验条件见表2,每种条件下重复做4次试验,取得了1 200组数据。

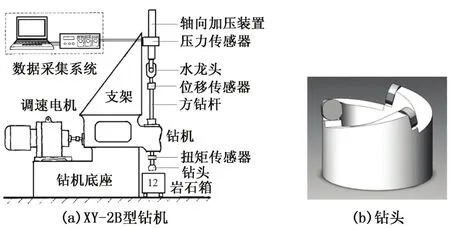
图1 试验装置Fig.1 Experimental equipment

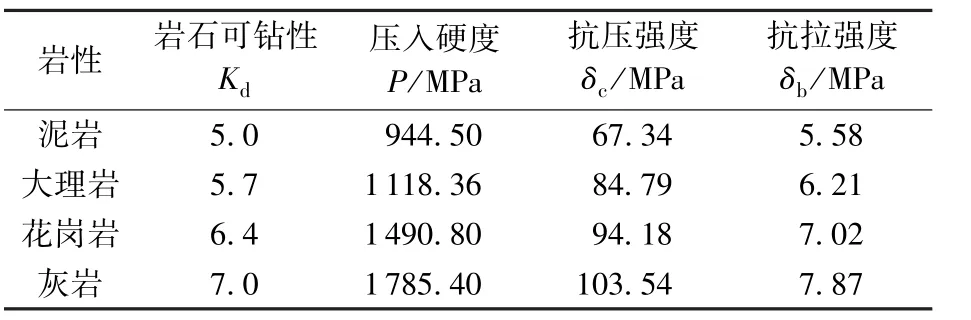
表1 岩石参数Table 1 Rock parameters

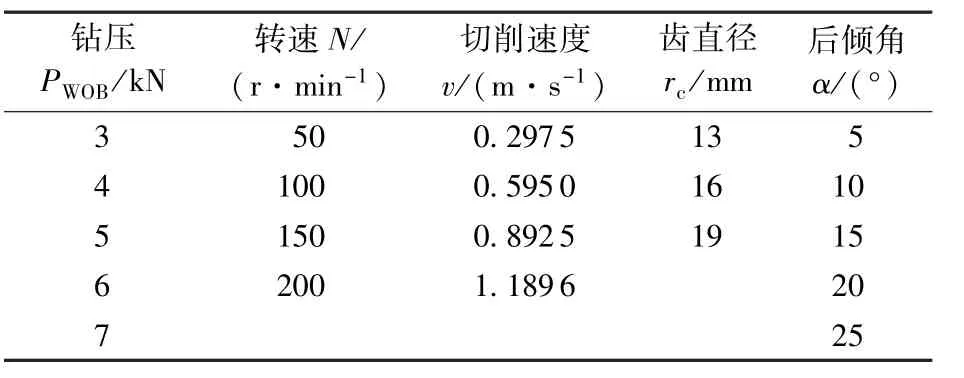
表2 试验条件Table 2 Experimental conditions

2 试验结果分析

2.1 聚类分析

本文中采用系统聚类法[7]将变化规律相近的变量归成类(图2)。由图2可见:切削力、正压力与吃入深度、接触弧长、切削面积、齿直径最先聚类,说明这些变量在12个变量中关系最为密切;岩石的可钻性与压入硬度、抗压强度、抗拉强度先聚为一类而后才与切削力、正压力聚类,这些变量都反映了岩石的强度特征。由于岩石可钻性可以综合反映岩石破碎的难易程度,所以在公式中只考虑岩石可钻性。

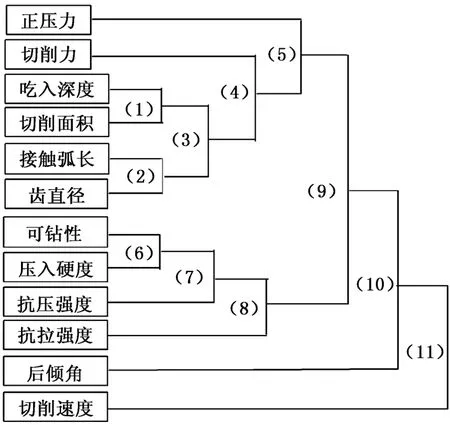
图2 聚类图Fig.2 Cluster analysis diagram

2.2 主成分分析

试验中变量太多将问题复杂化,为了找到影响切削齿受力的主要因素,对试验数据做主成分分析,变量的特征值及贡献率见表3。由表3可知切削力和正压力与切削面积的贡献率之和均大于76%,这说明切削面积是影响切削齿受力的主要因素。

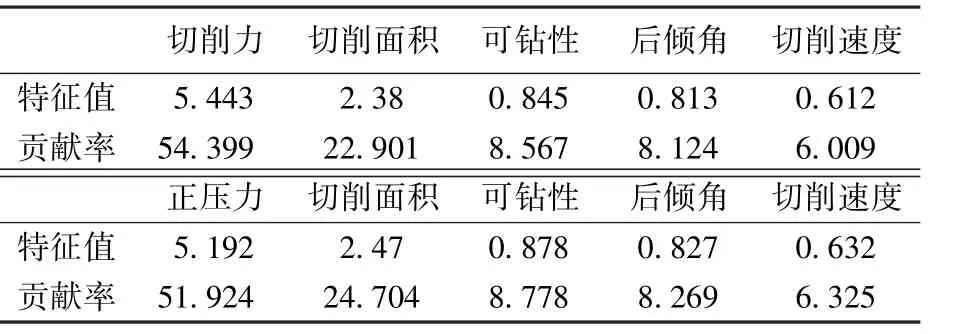
表3 变量的特征值及贡献率Table 3 Eigenvalues and contribution rate of variables

2.3 回归分析

2.3.1 切削面积与切削齿受力的关系

切削齿受力与切削面积的关系最为密切,利用回归分析可以确定二者之间的定量关系。正压力Fn、切削力Fc与切削面积A的关系曲线如图3(切削齿后倾角15°,切削速度0.2975 m/s)所示。当切削齿后倾角和岩石倾角相同时,切削齿的切削力、正压力随切削面积的增大呈线性增大。

根据图3可以建立切削齿受力与切削面积之间的关系,表达式为

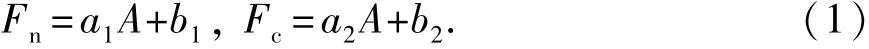
式中,a1、a2、b1、和b2为系数。

试验发现,在相同的切削面积和岩石性质下,加载钻压的试验与没有加载钻压的试验相比,其切削齿受力更大。实际钻井时切削齿在钻压下切削岩石,所以加载钻压的试验更符合实际情况。

2.3.2 切削速度与切削齿受力的关系

因为文献[4-6]中的试验刀具是前倾、尖锐、没有倒角和磨损的切削齿,所以认为可以忽略切削速度对切削齿受力的影响。但是,实际钻头使用的是后倾、有倒角的PDC切削齿,这些试验的结论不适用于PDC钻头。文献[8-10]的试验证明,当切削深度相同时,切削速度越大切削齿受力越大。

本文中对试验数据进行回归分析,确定切削速度与正压力、切削力的关系(图4,切削齿后倾角15°,泥岩)。当切削齿后倾角和地层岩石倾角相同时,在相同吃入深度下,切削齿的切削力、正压力都随切削速度的增大而增大,切削齿受力与切削速度呈对数关系。

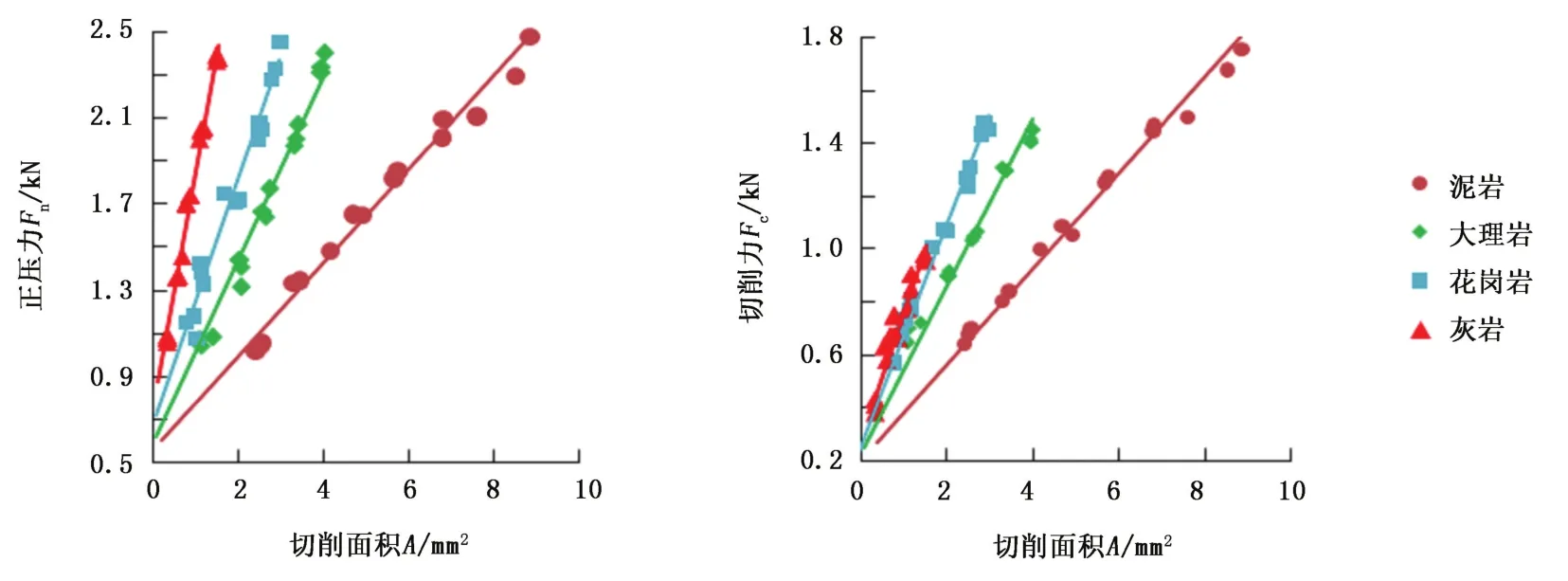
图3 正压力Fn、切削力Fc与切削面积A的关系Fig.3 Relationship of cutting areaAwith normal forceFnand tangential forceFc

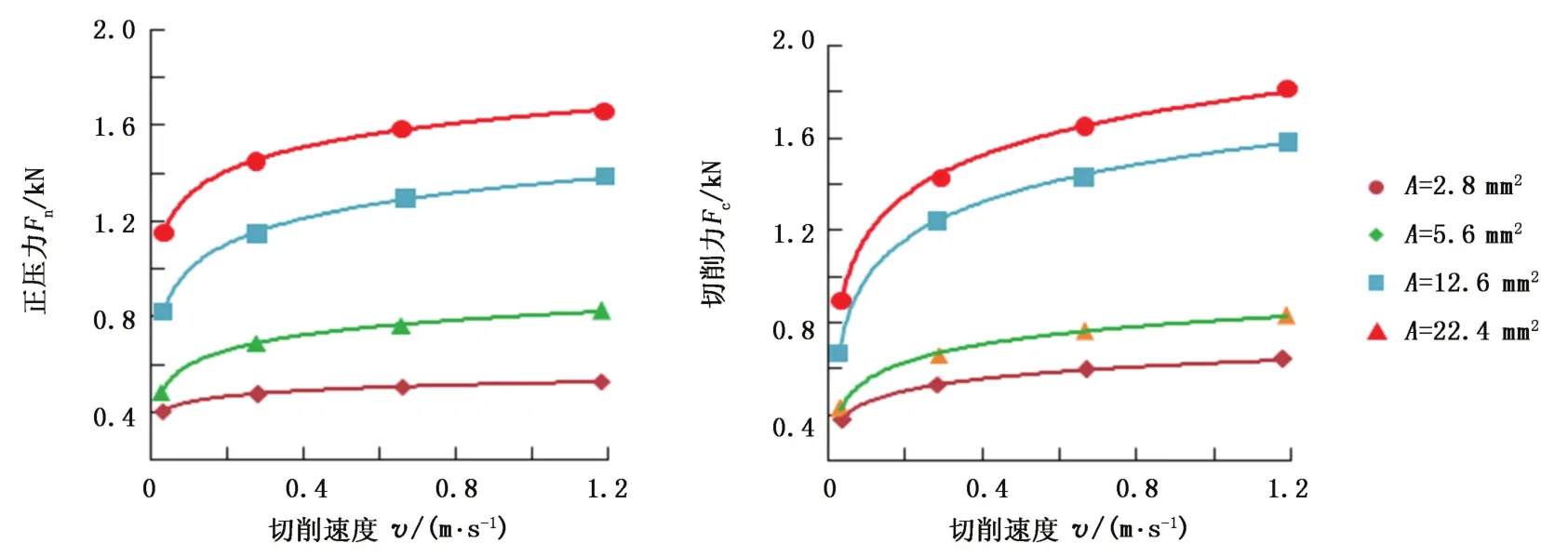
图4 正压力Fn、切削力Fc与切削速度v的关系Fig.4 Relationship of cutting velocityvwith normal forceFnand tangential forceFc

2.3.3 切削齿后倾角与切削齿受力的关系

在相同岩性和切削面积下,切削齿后倾角约为10°时,PDC切削齿受力最小,切削力和正压力随切削齿后倾角增大而增大,可以用二次函数拟合二者之间的关系。

2.3.4 岩石可钻性级值与切削齿受力的关系

在相同的切削齿后倾角和切削面积下,当岩石可钻性级值Kd增大时,切削齿的切削力和正压力随之增大,二者呈线性函数关系。

3 PDC切削齿与岩石相互作用理论模型

在做多元非线性回归分析之前,需要确定各变量与切削齿受力的关系式的形式。在试验和数值模拟的基础上,深入研究PDC切削齿的破岩机制,建立新的切削齿与岩石相互作用理论模型,由此说明新建公式的形式的合理性。

图5(a)为使用LS-DYNA有限元分析软件[13]对PDC切削齿切削岩石作动态分析得到的损伤云图。本模型主要考虑岩石的损伤与破坏,岩石采用MAT_CSCM材料,能够模拟脆性岩石的体积破碎。设岩石的密度为2 600 kg/m3,剪切模量为28 GPa,体积模量为38.1 GPa,抗压强度为112 MPa,将PDC切削齿设置为刚体。钻井时产生块状岩屑的原因是岩石沿着剪切面破坏,PDC切削齿将块状岩屑从岩石本体上切削下来。当切削齿向前做切削运动时,块状岩屑向前运动。在切削齿与块状岩屑之间的岩石由于挤压破坏形成岩粉破碎带。因为挤压作用,破碎带既不能向前运动又不能向后运动,只能留在切削齿表面上。

将块状岩屑简化为三角形,得到切削齿与岩石相互作用的二维理论模型(图5(b))。图5(b)中mn是剪切破坏面,淡黄色区域amn是块状岩屑,天蓝色区域abcn是岩粉破碎带。因为破碎带留在切削齿表面上,所以破碎带的垂直面an和水平面cn上受力等于切削齿正面ab和倒角面bc上的受力。橙色区域是齿后岩粉,cd是切削齿与齿后岩粉接触的面。

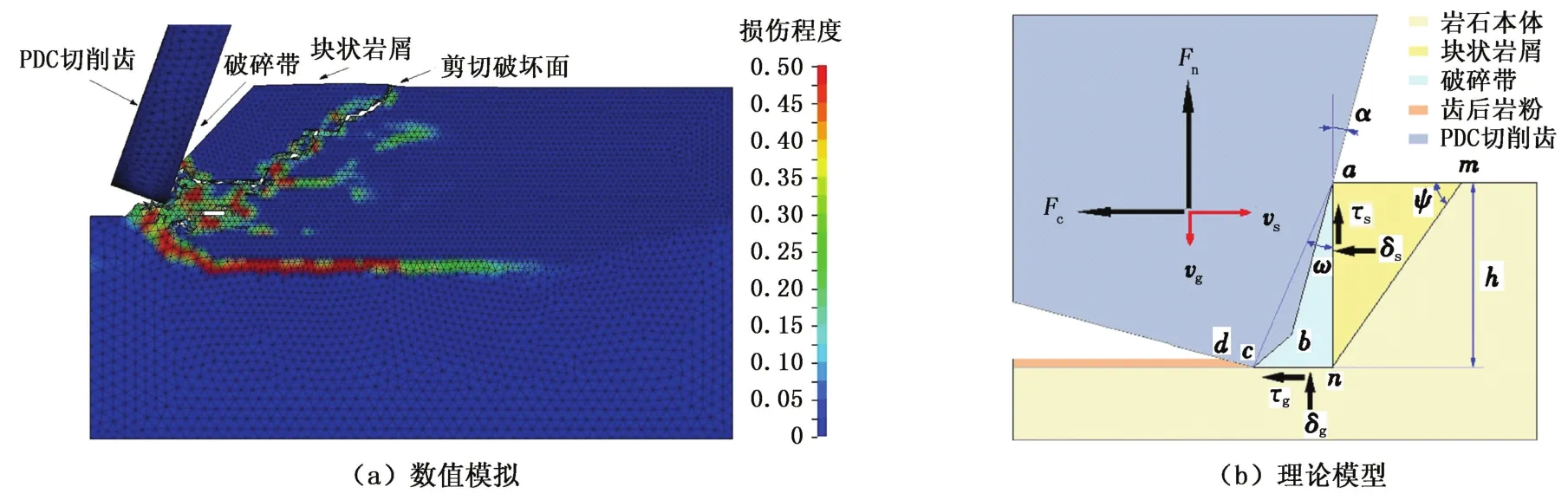
图5 PDC切削齿与岩石相互作用模型Fig.5 Interaction model of PDC cutter and rock

本文中认为破碎带中的岩粉为颗粒物质,破碎带是大量离散的岩屑颗粒相互作用而形成的复杂体系,其力学特性不同于普通的固体和液体。岩屑颗粒是构成破碎带的骨架、传递载荷的基本单元,其与颗粒间的孔隙水共同决定了破碎带的应力路径、非线性本构关系和剪切膨胀等复杂特征。在运动速度与岩屑颗粒和固体表面之间作用力的关系方面,Behringer等[11]的研究取得了突破。他们利用光弹性应力分析法做了二维环剪试验、二维活塞试验和二维双轴试验,利用颗粒物质动力学原理解释了这些试验现象并建立了速度与应力的关系模型,发现对于不可逆的塑性变形,应力与速度有关,当速度变大时,颗粒间的应力增大,速度与应力呈对数关系。

将该理论应用到破碎带上[9]。图5(b)中,已知切削齿有向前的切削速度vs和向下的切削速度vg,岩粉破碎带的垂直面an上均布着正应力δs和剪应力τs。根据摩尔库伦准则[12]对图5(b)的剪切破坏面mn进行受力分析可得正应力σs和剪应力τs的计算公式为

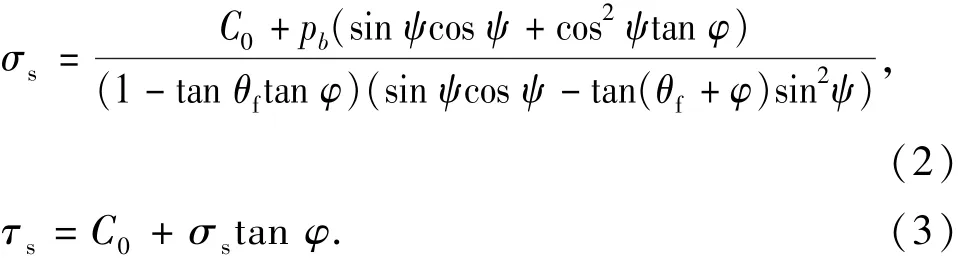
式中,C0为岩石内聚力;φ为岩石的内摩擦角;pb为钻井液压力;θf为切削齿与岩石的摩擦角;ψ为块状岩屑三角形的角度。

破碎带水平面cn上均布着正应力δg和剪应力τg。正应力δg与切削速度vg的关系式为

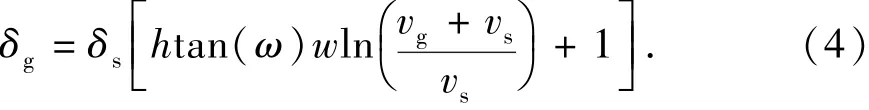
式中,ω为∠can的角度;h为线段an长度;htanω为线段cn长度;w为接触弧长。根据库伦摩擦定理[9],正应力σg和摩擦系数μg之间的关系式为

其中,μ0、Σ1和Σ2为cn面上的拟合参数。则剪应力τg为

将切削齿受力分解为3个部分:an面上的正压力Fcn和切削力Fcc;cn面上的正压力Fdn和切削力Fdc;切削齿后部cd面上的正压力F0n和切削力F0c。则有:

其中fn和fc是与岩石可钻性、切削齿后倾角和切削速度有关的系数。则整个切削齿的正压力Fn和切削力Fc为式(10)即为切削齿与岩石相互作用理论模型,切削齿受力与切削速度呈对数关系。

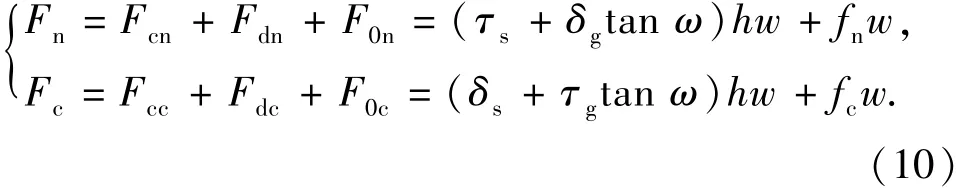
4 PDC切削齿受力计算模型

有关岩石性质的θf、ψ、φ等参数在试验室中容易获得,但是在钻井现场不易获得,所以式(10)有不足之处。岩石可钻性可在钻井现场获得,因此需要建立基于岩石可钻性的计算模型。

由于是在切削齿的微小表面上求切削齿受力,吃入深度h与接触弧长w的乘积近似等于切削面积A,所以可以只考虑切削面积A和接触弧长w。对比式(10),对试验数据进行多元非线性回归,式(1)可以改写为

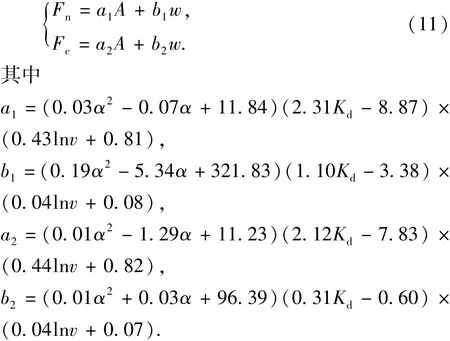
在多元非线性回归中,整体方差R2=0.954,符合工程要求。表4为切削齿受力的计算值与实测值的对比,可见二者吻合较好,说明切削齿受力计算模型精度较高。

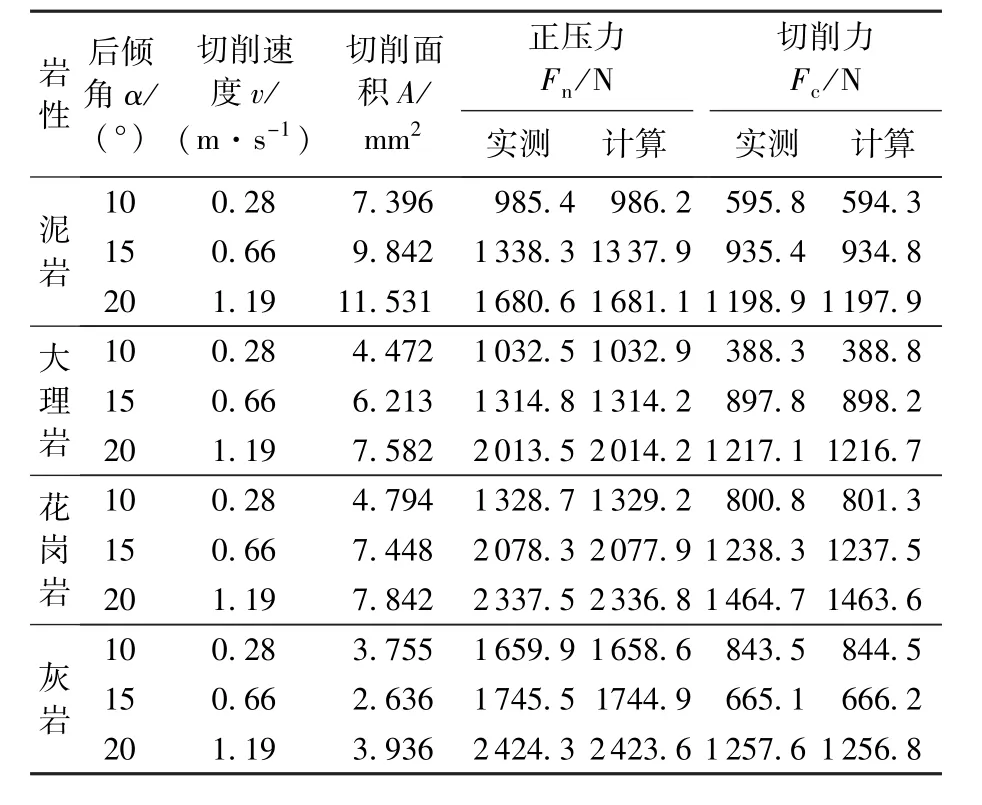
表4 切削齿受力的计算值与实测值对比Table 4 Experimental data and calculated value of force of cutters

5 结 论

(1)切削面积是影响切削齿受力的主要因素。(2)加载钻压的试验更符合实际情况。

(3)切削齿受力随切削面积、岩石可钻性级值的增大而增大,呈线性函数关系。切削齿受力与切削齿后倾角呈二次函数关系。

(4)在相同吃入深度下,切削齿受力随切削速度的增大而增大,并且切削齿受力与切削速度呈对数关系。

(5)将颗粒物质动力学理论应用到岩粉破碎带上,从理论上验证了切削齿受力与切削速度呈对数关系。

[1] 邹德永,张将海,王瑞和.PDC钻头力学模型的试验研究[J].石油钻探技术,2005,33(2):41-43.

ZOU Deyong,ZHANG Jianghai,WANG Ruihe.The experiment study on mechanical model of PDC bits[J]. Petroleum Drilling Techniques,2005,33(2):41-43.

[2] 马清明,王瑞和.PDC切削齿破岩受力的试验研究[J].中国石油大学学报:自然科学版,2006,30(2): 45-47.

MA Qingming,WANG Ruihe.Experimental study on force of PDC cutter breaking rock[J].Journal of China University of Petroleum(Edition of Natural Science), 2006,30(2):45-47.

[3] 邹德永,王瑞和,岳志国.PDC钻头的轨迹方程及切削参数计算方法[J].石油钻采工艺,2003,25(5):34-38.

ZOU Deyong,WANG Ruihe,YUE Zhiguo.Trace equation and methods for computing cutting parameters of PDC bits[J].Oil Drilling&Production Technology,2003,25 (5):34-38.

[4] FAIRHURST C.Some possibility and limitations of rotary drilling in hard rocks[J].Transaction of the Instruction of Mining Engineers,1955,1115:85-103.

[5] GRAY K E,ARMSTRONG F,GATLIN C.Two-dimensional study of rock breakage in drag-bit drilling at atmospheric pressure[J].Journal of Petroleum Technology, 1962,14(1):93-98.

[6] ROXBOROUGH F F,ROXBOROUGH F F,PEDRONCELL E J.A Practical evaluation of some coal cutting theories using a continuous miner[J].The Mining Engineer,1982,11:145-156.

[7] 张厚美,吴何洪.岩石力学特性关系的探讨[J].中国海上油气:工程,1999,11(3):46-50.

ZHANG Houmei,WU Hehong.Investigate the relationship between the mechanical properties of the rock[J]. China Offshore Oil and Gas(Engineering),1999,11 (3):46-50.

[8] DAGRAIN F,TSHIBANGU J P.Use of the D3 model for the estimation of forces acting on a cutter in rock cutting and drilling[R].SPE 78242,2002.

[9] PELFRENE G,SELLAMI H,GERBAUD L.Mitigating stick-slip in deep drilling based on optimization of PDC bit design[R].SPE 139839,2011.

[10] 董海,张弘韬.切削速度对岩石切削力的影响[J].金刚石与磨料磨具工程,1999(1):21-23.

DONG Hai,ZHANG Hongtao.Study on the impact of cutting speed on the force of cutting rock[J].Diamond &Abrasives Engineering,1999(1):21-23.

[11] HARTLEY R R,BEHRINGER R P.Logarithmic rate dependence of force networks in sheared granular materials[J].Nature,2003(421):928-931.

[12] GERBAUD L,MENAND S,SELLAMI H.PDC bits: all comes from the cutter rock interaction[R].SPE 98988,2006.

[13] JAIME M C.Numerical modeling of rock cutting and its associated fragmentation process using the finite element method[D].The Swanson School of Engineering,University of Pittsburgh,2012.

(编辑 李志芬)

Interaction model of PDC cutter and rock

WANG Jiajun,ZOU Deyong,YANG Guang,HE Renqing,CHEN Xiuping
(School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China)

A series of drilling experiment were carried out by using experimental equipment,in which load on cutters can be increased.Experiments were conducted with various load,cutting area,cutting speed,back dip angle of PDC cutter and rock properties.The experimental results were analyzed with multiple nonlinear regression technique and a new cutter-rock interaction model was proposed.The results show that the cutter area is the principal factor influencing the force of cutters. The force of cutters increases with cutting area,back dip angle of PDC cutter and rock drillability.It is a logarithmic relationship between the force of cutters and cutting speed.

PDC bits;cutters;interaction model;drilling rate;weight on bit

TE 21

A

1673-5005(2014)04-0104-06

10.3969/j.issn.1673-5005.2014.04.015

2013-12-08

国家“十二五”科技重大专项(05Z12020300);中国石油大学(华东)自主创新基金项目(12CX06025A)

王家骏(1983-),男,博士研究生,主要从事油气井工程岩石力学研究。E-mail:wangjiajun1983@163.com。

王家骏,邹德永,杨光,等.PDC切削齿与岩石相互作用模型[J].中国石油大学学报:自然科学版,2014,38 (4):104-109.

WANG Jiajun,ZOU Deyong,YANG Guang,et al.Interaction model of PDC cutter and rock[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):104-109.