基于PSCAD/EMTDC软件的配电线路感应过电压计算方法

陈继明,朱明晓,王 辉,仉志华

(中国石油大学信息与控制工程学院,山东青岛 266580)

基于PSCAD/EMTDC软件的配电线路感应过电压计算方法

陈继明,朱明晓,王 辉,仉志华

(中国石油大学信息与控制工程学院,山东青岛 266580)

对配电线路的感应过电压及耐雷性能进行研究。通过相模变换将Agrawal模型转换为模量的波动方程,根据特征线法对波动方程进行分析,得到感应过电压的等值计算电路,并对雷电电磁场的计算方法进行简化。建立感应过电压在PSCAD/EMTDC软件中的计算模型,与数值计算方法比较以验证模型的准确性,分析土壤电阻率对感应过电压的影响及避雷器、耦合地线降低感应过电压的效果。结果表明,应对土壤电阻率较高地区配电线路重点保护;线路绝缘水平较低时(150 kV)要有效降低感应过电压,在土壤电阻率较低、较高时避雷器间距分别不宜大于400 m、200 m,绝缘水平较高(300 kV)且土壤电阻率较高时,避雷器间距不宜大于400 m;耦合地线与线路高度差越小,降低感应过电压效果越明显。

架空配电线路;感应过电压;计算模型;土壤电阻率;防雷措施

架空配电线路绝缘水平较低,感应雷是造成绝缘闪络的重要原因[1-4],对配电网的安全可靠运行造成很大威胁,感应过电压的计算分析意义重大。目前,中国计算感应雷过电压的方法主要有规程法[5]和数值计算方法[6-9]两种。规程法使用经验公式计算感应过电压的幅值,实际运行结果表明,其计算结果存在一定偏差[10-11],且不能对感应过电压波形进行分析;数值计算方法通过编程计算雷电电磁场及求解场线耦合模型计算感应过电压,计算结果比较精确,但是由于边界条件处理复杂,计算安装避雷器、架设耦合地线及多分支线路的感应过电压较困难,且线路空间分布变化时需要修改程序,因此不易对不同防雷措施下的雷击性能进行分析与比较,从而确定合理的防雷措施。在感应过电压特性分析方面,文献[1-2,6-7]主要分析了线路高度、回击速度、落雷点位置及雷电流波形等因素对感应过电压的影响,但对避雷器及耦合地线等措施抑制感应过电压的作用方面分析仍不足。PSCAD/EMTDC及EMTP等电磁暂态软件中包含许多现成的设备模型,在线路反击及绕击耐雷性能分析中获得了广泛应用,但是由于雷电电磁场及线路耦合模型分析较复杂,该类软件中未集成感应过电压的计算模块。笔者通过相模变换将Agrawal模型转换为模量的波动方程,根据特征线法对波动方程进行分析,得到感应过电压的等值计算电路,并对雷电电磁场的计算进行简化,在PSCAD/EMTDC软件中建立感应过电压的计算模型,分析土壤电阻率对感应过电压的影响及避雷器、耦合地线降低感应过电压的效果。

1 感应过电压计算模型

雷电感应过电压的计算主要包括雷电电磁场的计算及场线耦合模型的求解两部分。

1.1 雷电电磁场的计算

1.1.1 工程回击电流模型

工程回击模型(图1)中,将雷击通道等效为垂直于大地的直通道,并根据数学表达式确定了雷电通道各处电流的时空分布,不同的回击模型可以归纳为以下表达式[12]:

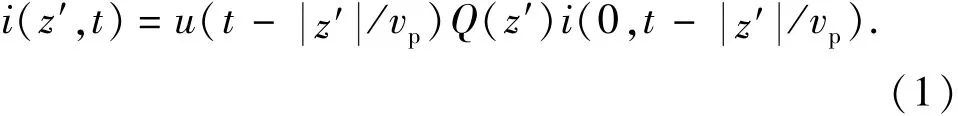
式中,u为Heaviside函数,当t≥p时u=1,否则u=0;Q(z′)为与高度有关的雷电流衰减系数;i(0,t)为雷电通道基电流;z′为雷电通道中某一点的z轴坐标;vp为雷电回击速度;本文中选择改进的传输线模型(MTLE),Q(z′)=exp(),λ一般取为1.7～2.0 km。

目前,雷电流多使用双指数函数与Heidler函数模拟,但双指数函数在t=0时导数不为0,与实际观测的雷电流不符,而且在雷电电磁场的计算中雷电流在t=0时的导数不易确定[13]。因此,在感应过电压的计算中,雷电通道基电流多使用Heidler函数模拟[2,12]:

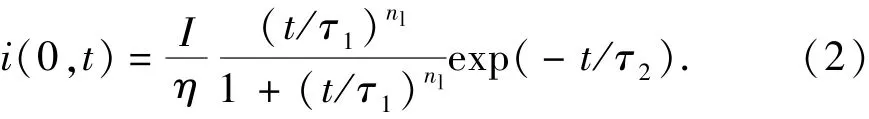
其中

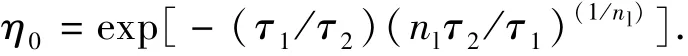
式中,I为雷电流幅值;τ1和τ2分别为波前时间常数和半波长时间常数;nl为雷电流前沿陡度系数;η0为修正系数。

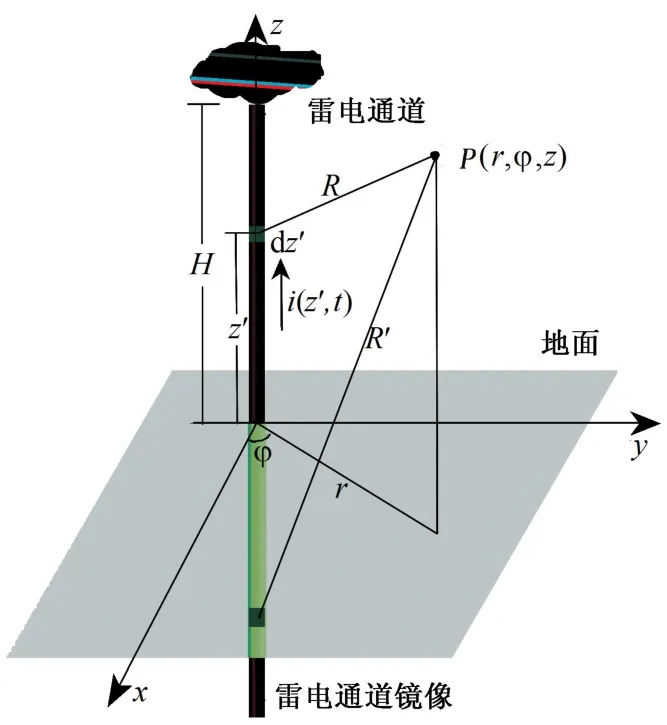
图1 雷电回击模型Fig.1 Lightning return stroke model

1.1.2 雷电回击电磁场的计算

在Master和Uman将大地假设为理想导体的基础上,根据Maxwell方程推导了空间某点P(r,φ,z)(图1)电场水平、垂直分量及横向磁场分量的计算公式:

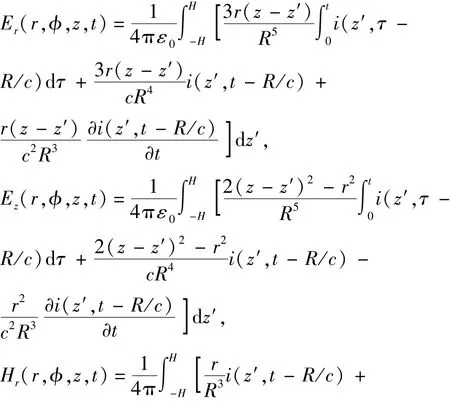
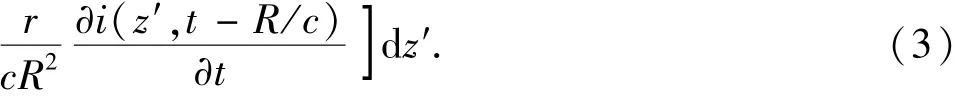
式中,ε0为真空介电常数;c为光速;r、φ和z分别为P点的径向坐标、方位角及轴向坐标;H为雷电通道高度;R=。

含有电流积分的项为静电场分量,电场水平、垂直分量中的静电场分量设为ErS(r,φ,z,t)、EzS(r,φ,z,t)。该项包含τ和z′的双重积分,所需计算时间较长,如果交换静电场中τ和z′积分顺序,可以避免对z′积分时τ积分的多次重复计算,减少计算时间。

假定时间步长为Δt,则t=nΔt(n=0,1,…,N),对空间某点P(r,φ,z),ErS(nΔt)及EzS(nΔt)按以下递推公式计算:

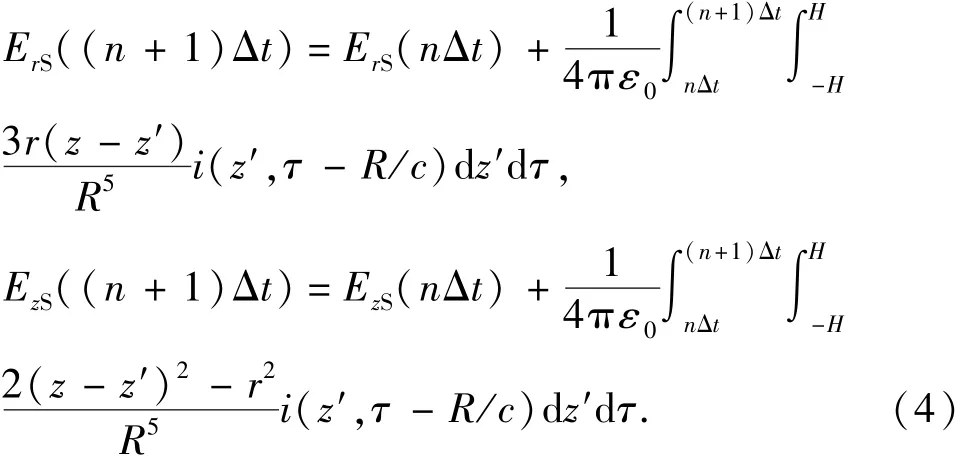
式中,n(n=0,1,…,N)表示第n个计算步长,对应的时间t=nΔt。

1.1.3 考虑土壤电阻率影响时的雷电电磁场

考虑土壤电阻率影响时,电场垂直分量和磁场变化不大,但对电场水平分量影响较大,偶极子法计算的电场水平分量偏差较大,一般使用Cooray-Rubinstein公式[14-15]对偶极子法计算得到的电场水平分量进行调整:

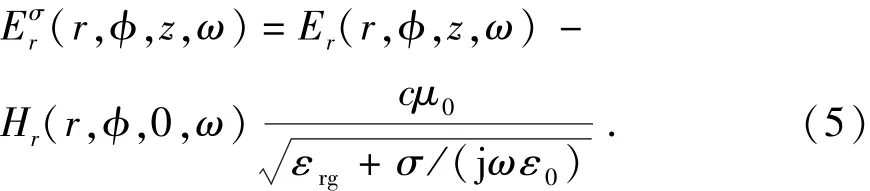
其中

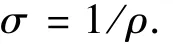
式中,(r,φ,z,ω)为考虑土壤电阻率影响时的水平电场;μ0为真空磁导率;σ为大地电导率,S/m;ρ为土壤电阻率;εrg为土壤相对介电常数。

式(5)为频域表达式,使用傅里叶逆变换不易得到解析解,不能应用到时域计算中。文献[16]使用矢量匹配法将式(5)对应的复频域表达式分解为NRA(NRA=12)个有理分式相加的形式,推导得到式(5)的近似时域表达式:

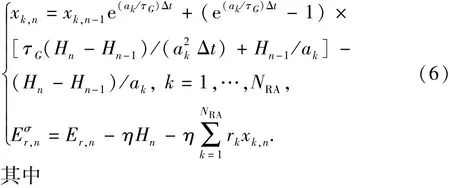
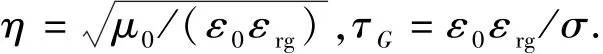
式中,x为推导中设置的中间变量;ak、rk分别为有理分式的极点和留数,具体取值见文献[14],k表示极点与留数的序号;η、τG为常数;Hn为nΔt时刻(r,φ,0)处的横向磁场分量;Er,n、Eσr,n为考虑大地电阻率前后nΔt时刻(r,φ,z)处的电场水平分量。

1.2 场线耦合模型的求解

Nucci[17]和Cooray[18]对多种电磁场与线路的耦合模型进行了比较,认为Agrawal模型[19]是最准确的模型,本文中使用该模型分析感应过电压。多导线线路的Agrawal模型为

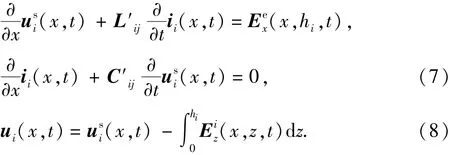
式中,L′ij、C′ij分别为导线单位长度电感和电容矩阵的元素;(x,t)、ui(x,t)为散射电压及线路总电压;ii(x,t)为线路电流;(x,hi,t)、(x,z,t)为入射电场水平、垂直分量。

对(x,t)、ii(x,t)进行相模变换,得到模量上的Agrawal波动方程为

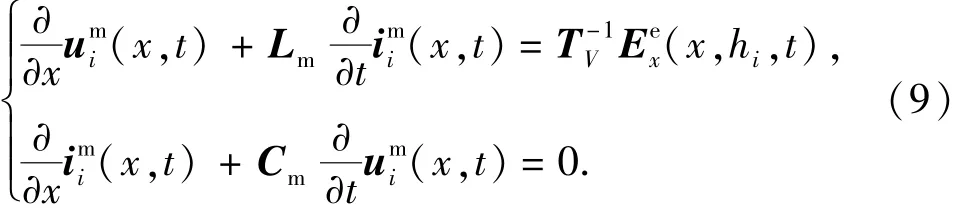
式中,Lm、Cm分别为模量上的电感、电容矩阵,LmI,Cm=TI-1C′ijTV;TV、TI为散射电压、电流变换矩阵,由于0ε0In,可取TV=TI=T,矩阵T根据雅可比法计算。此时,Cm=μ0ε0Lm-1,模量波速度为v=1/=c,模量特征阻抗矩阵ZCi=

LIETDOS-BIO是一款用来评价立陶宛核电站所产生的污染问题的软件。该模型使用两种浓集因子数据库：因场地而异的数据库以及通用数据库(主要基于欧盟FASSET中的数据以及源自俄语文献的数据)。该软件采用蒙特卡洛辐射转移模型，一种经特殊衍变而来的描述有机体模型的方法使得用户能够针对任何大小和形状的有机体计算剂量转换因子。该模型中参数的不确定性用统计学方法来进行处理。

假定某段线路两端的坐标为x1、x2(x1＜x2),使用文献[20]的特征线法对式(9)进行求解,得

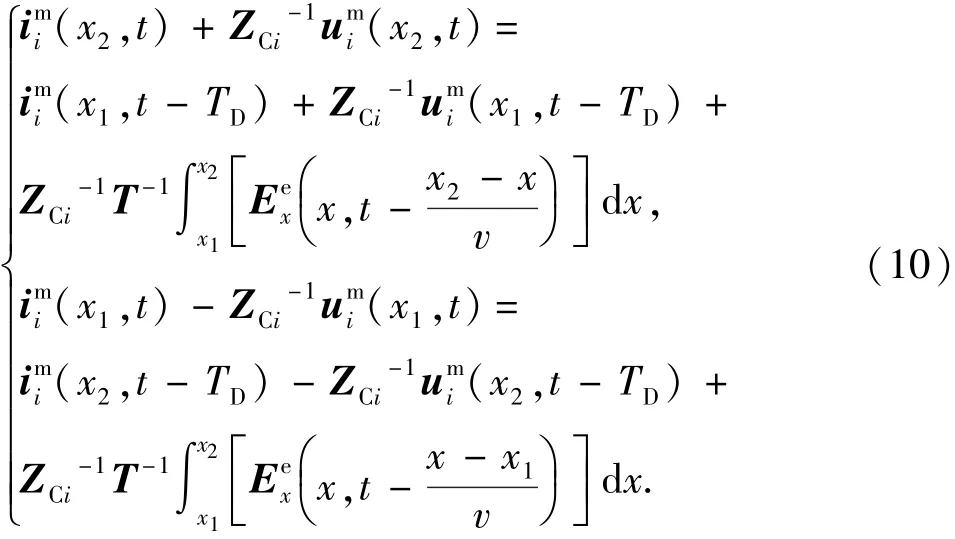
式中,TD为波由线路一端到另一端的传播时间,TD=(x2-x1)/v。式(10)为模量上的表达式,对其进行相模变换反变换,得到相量上的表达式

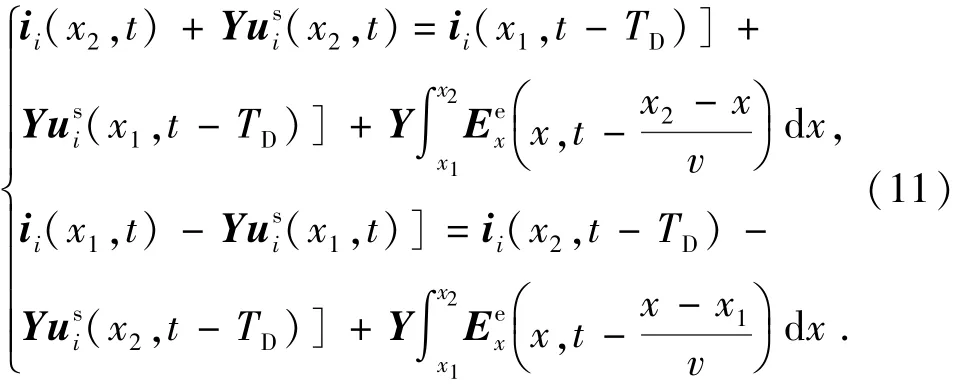
式中,矩阵。式(11)可以使用诺顿等效电路实现,如图2所示(以三相线路为例),则两等效受控电流源数值、根据式(11)右侧计算,具体计算式如下式所示:

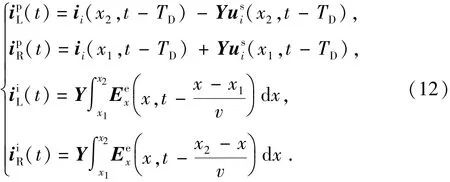
式中,及反映了由线路另一端传播过来的波对本端线路的作用,及反映了电场水平分量的作用;电阻RA、RB、RC、RAB、RBC、RAC根据导纳矩阵Y求得。

式(11)中电压为散射电压,根据式(8)计算线路总的电压,不同高度处雷电垂直电场基本相等,因此式(8)可表示为

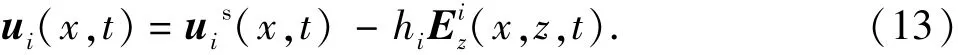
其中,线路两端对应的,z,t)使用电压源、模拟,反映了电场垂直分量对线路的作用。最后得到完整的感应过电压等值计算电路如图2所示。

1.3 感应过电压在PSCAD/EMTDC的计算

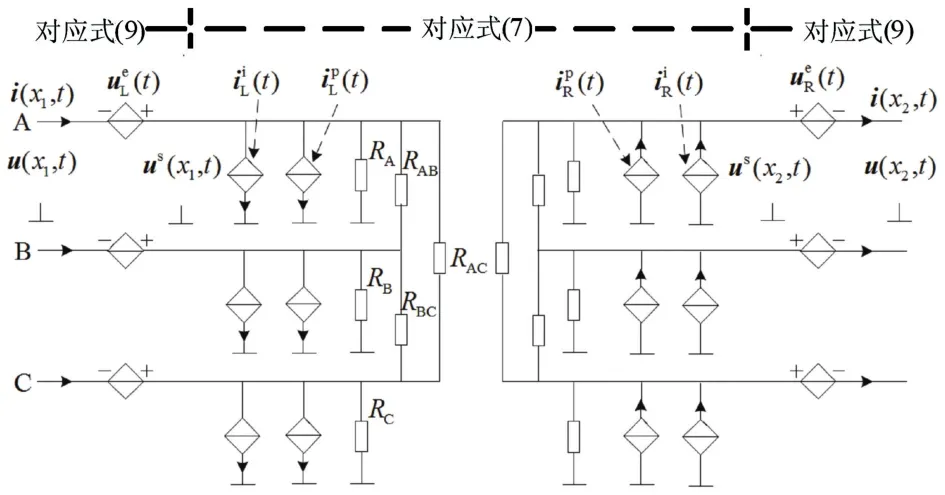
图2 感应过电压等值电路Fig.2 Equivalent calculation circuit of lightning induced overvoltage

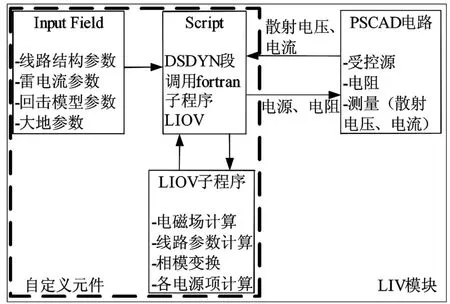
图3 感应过电压在PSCAD中的计算模型Fig.3 Calculation model of lightning induced overvoltage using PSCAD

1.4 减少计算时间的方法

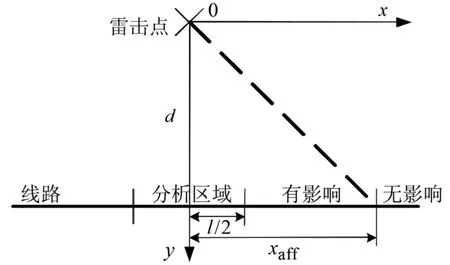
图4 减少计算时间的方法Fig.4 Method of reducing calculation time

如图4所示,长度为l的线路段距离雷击点最近,感应过电压最大,很多情况下只需对该段线路感应过电压进行分析。但线路两端的反射波会对该段线路电压产生影响,因此使用LIV模块模拟的线路应足够长。假定xaff为在时间Ts内反射波会产生影响的最大线路坐标,则aff段线路可以使用匹配电阻模拟,简化后由此产生的反射波在仿真时间Ts传播不到“分析区域线路段”,因此不会对其感应过电压产生影响,可以节省计算段线路雷电电磁场的大量时间。根据波速v=c,则

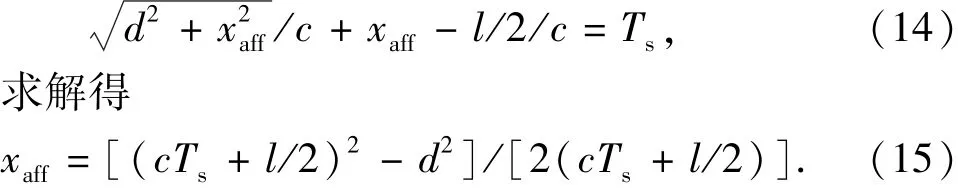
2 计算模型的验证

文献[21]使用数值计算的方法计算了图5所示线路的感应过电压,线路长度1 km,雷击点位于线路中间,与线路垂直距离50 m。雷电流使用两个Heidler模型之和模拟,幅值为12 kA,最大陡度为40 kA/μs;雷电回击速度为1.3×108m/s;R等于各导线单独存在时的波阻抗。选取相同的参数,使用本文模型计算图5线路过电压,图6(a)、(b)分别为文献[21]及本文中计算得到线路端点感应过电压波形。由图中可以看出,本文感应过电压波形与文献[21]波形基本一致,验证了本文方法的准确性。

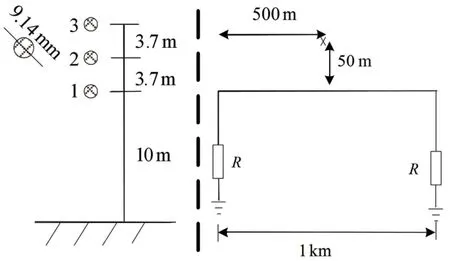
图5 线路结构示意图Fig.5 Configuration of conductors on tower

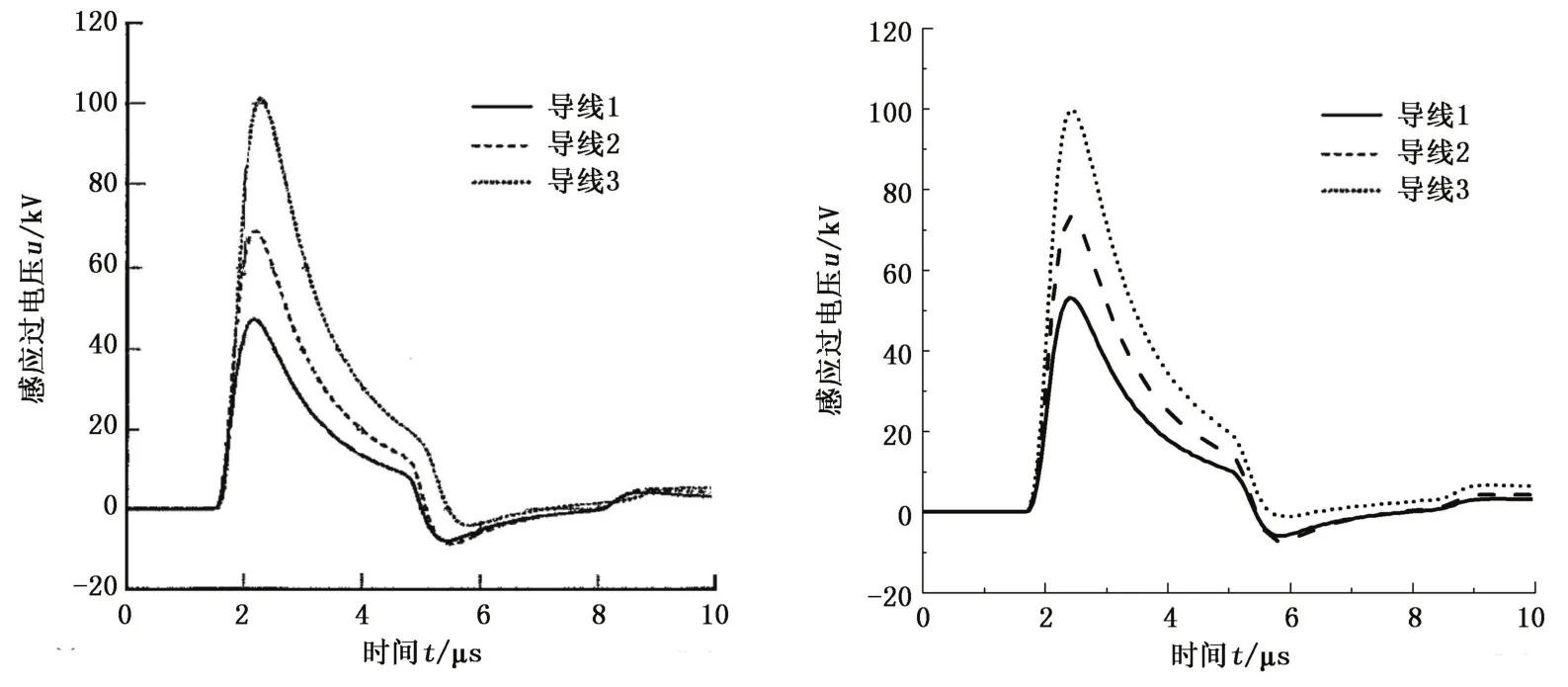
图6 感应过电压波形Fig.6 Calculation curve of lightning induced overvoltage

3 感应雷过电压特性分析

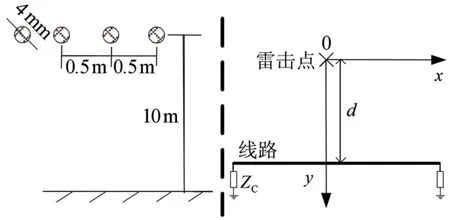
图7 线路结构示意图Fig.7 Configuration of conductors on tower

使用本文方法对图7所示线路的感应过电压特性进行分析,其中d为雷击点距线路垂直距离,ZC代表线路波阻抗矩阵,雷击点与线路两端距离相同,线路应足够长以避免反射波对线路中间位置感应过电压的影响。雷电流波前时间2.6 μs,波长时间50 μs;回击模型选择改进的传输线模型,回击速度为1.3×108m/s。规程给出雷电流幅值IM概率分布为:lgP=-I/88,其中,P为IM＞I(kA)的概率,则IM＞60 kA的概率为0.2,对线路的危害较严重,根据文献[22]电气几何模型,IM=60 kA时,雷击点距线路垂直距离d＞81 m时雷击大地,从严考虑,本文中取IM=60 kA,d=70 m。

以图7所示线路分析土壤电阻率ρ对感应过电压的影响,ρ=0及ρ=1 000 Ω·m时线路各处感应过电压波形如图8(a)、(b)所示。由图中可以看出,距离雷击点最近的线路处感应过电压最大;ρ对感应过电压影响很大,ρ=1000 Ω·m时感应过电压最大值较ρ=0时增大,因此应对ρ较高地区的线路重点防护;ρ=0时,线路各处感应过电压幅值接近,ρ=1000 Ω·m时各处差异很大,距离雷击点较近线路感应过电压增大,距离雷击点较远线路感应过电压出现负值,且幅值减小。

以图7所示线路分析避雷器以不同间隔d等间距均匀安装时对线路感应过电压的影响,避雷器型号为HY5WS-15/45.6,其特性使用IEEE模型模拟。图9给出了d=600 m时建模示意图,三相线路使用单线表示,仿真时间Ts取15 μs,距离雷击点最近的线路点M感应过电压最大,因此仅需测量该处电压,M点两侧线路长度取为2.5 km,在时间Ts=15 μs内线路两端反射波不会对M点感应过电压产生影响,线路两端连接匹配电阻,包括RA、RB、RC、RAB、RBC、RAC,各电阻连接方式与图2一致。仿真结果表明,距离M点最近的3组避雷器对其感应过电压影响较大,因此本文中只考虑距离M点最近的3组避雷器的影响。

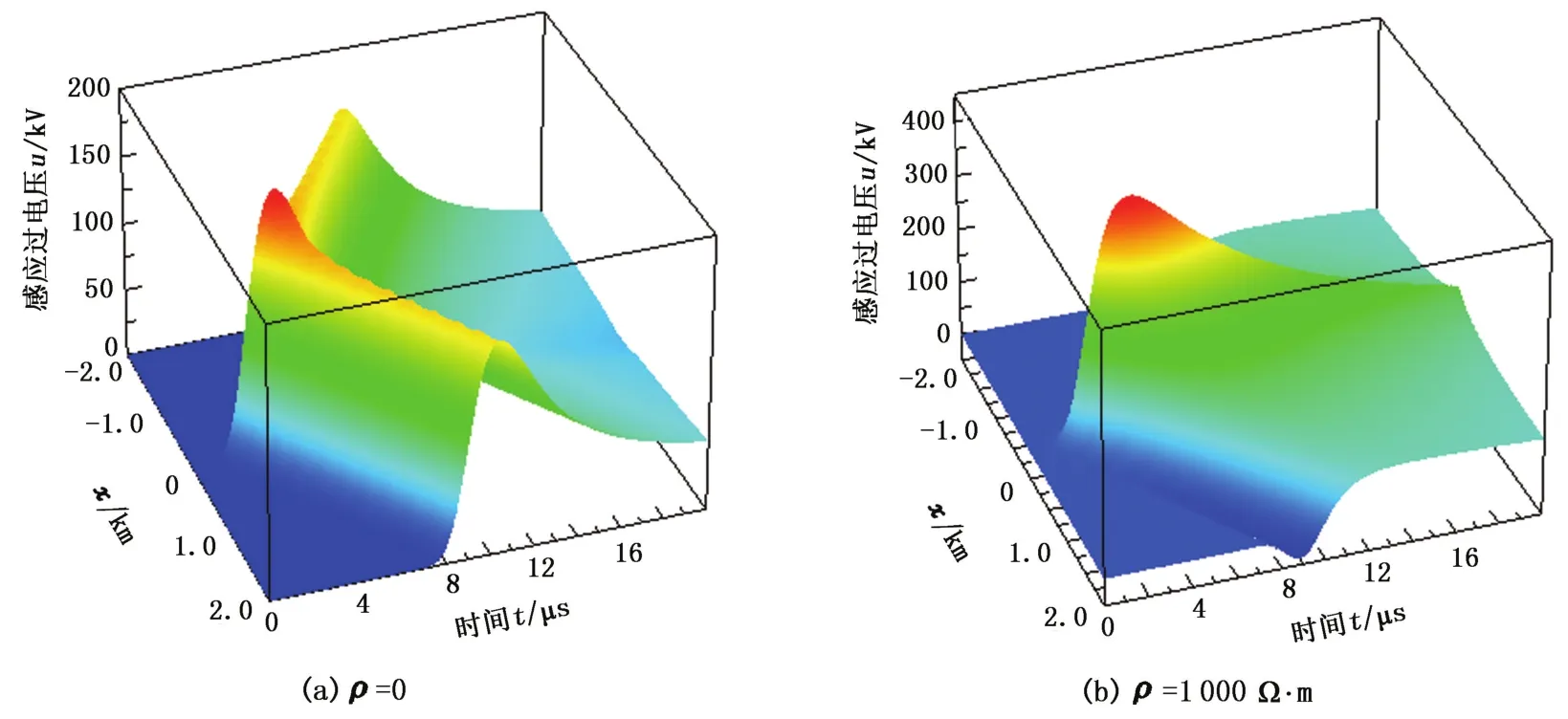
图8 感应过电压波形Fig.8 Calculation curve of lightning induced overvoltage

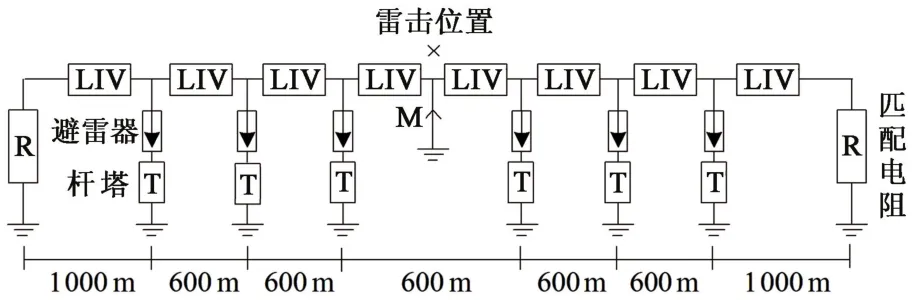
图9d=600 m时计算模型示意图Fig.9 Calculation model whend=600 m

图10 避雷器间隔对感应过电压的影响Fig.10 Influence of arrester installation spacing on lightning induced overvoltage

图10为不同避雷器安装间隔下ρ=0、ρ=1 000 Ω·m时M点感应过电压。假定线路的绝缘水平为150 kV,ρ=0、无避雷器时感应过电压幅值为200 kV,易造成绝缘闪络,d=400 m时的感应过电压幅值降为135 kV,采用IEEE标准[22]中比较过电压幅值与线路绝缘水平作为绝缘子是否闪络的判据,此时过电压幅值低于线路绝缘水平,不会造成绝缘闪络,ρ=1 000 Ω·m时感应过电压增大,只有d＜200 m时感应过电压幅值才能降至150 kV以下,绝缘子才不会闪络;如果线路绝缘水平为300 kV时,ρ=0时感应过电压对线路影响很小,可不采取防雷措施,ρ=1000 Ω·m只有当d＜400 m时线路的感应过电压幅值才能降到线路绝缘水平以下。

以图7所示线路为例,分析耦合地线高度hg对感应过电压的影响,计算结果如图11所示。由图中可以看出耦合地线可以降低感应过电压,而且降低程度与hg有关,hg=10.5 m时,耦合地线与线路高度差最小,此时感应过电压幅值为120 kV,降为无耦合地线时的0.6倍,由于在其他高度下,耦合地线与线路距离较大,降低感应过电压效果减弱;与线路距离相同但位于线路上方时降低感应过电压更大,因为此时耦合地线的感应过电压较大,降低线路电压更明显。

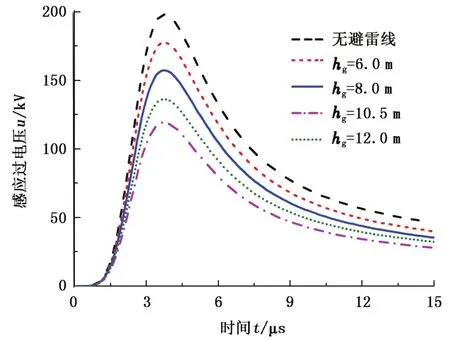
图11 耦合地线高度对感应过电压影响Fig.11 Influence of coupling ground wire on lightning induced overvoltage

4 结 论

(1)使用相模变换及特征线法对Agrawal耦合模型进行分析,建立了感应过电压在PSCAD/EMTDC中的计算模型,并验证了该模型的准确性,该模型可以对安装避雷器、架设耦合地线等措施下线路及配电网的感应过电压进行分析。

(2)土壤电阻率使感应过电压增大,因此应对土壤电阻率较高地区线路重点保护。

(3)避雷器可以有效降低感应过电压,对于绝缘水平较低线路(150 kV),要想有效降低感应过电压,土壤电阻率较低、较高时避雷器间距分别不宜大于400、200 m,对于绝缘水平较高(300 kV)线路,土壤电阻率较高时,避雷器间距不宜大于400 m,较低时无需安装避雷器。(4)耦合地线可以有效降低感应过电压,且与线路高度差越小效果越明显,而且耦合地线高度高于线路时比低于线路时效果更明显。

[1] 王希,王顺超,何金良,等.10kV配电线路的雷电感应过电压特性[J].高电压技术,2011,37(3):599-605.

WANG Xi,WANG Shunchao,HE Jinliang,et al. Characteristics of lightning induced overvoltage of 10kV distribution lines[J].High Voltage Engineering,2011, 37(3):599-605.

[2] 李琳,齐秀君.配电线路感应雷过电压计算[J].高电压技术,2011,37(5):1093-1099.

LI Lin,QI Xiujun.Calculation of the lightning induced voltages on power distribution lines[J].High Voltage Engineering,2011,37(5):1093-1099.

[3] 刘广孚,席文静,刘小华,等.基于数字信号处理器的潜油电泵机组转速测量系统的设计[J].中国石油大学学报:自然科学版,2009,33(1):154-161.

LIU Guangfu,XI Wenjing,LIU Xiaohua,et al.Design of rotation speed measurement system for electric submersible pumps based on digital signal processor[J]. Journal of China University of Petroleum(Edition of Natural Science),2009,33(1):154-161.

[4] 唐炬,欧阳有鹏,王存超,等.模拟气体绝缘组合电器产生不同局部放电的试验装置研制[J].重庆大学学报,2010,33(11):39-45.

TANG Ju,OUYANG Youpeng,WANG Cunchao,et al. Study on testing device for simulating the partial discharges of different defects in gas insulated switchgear[J]. Journal of Chongqing University,2010,33(11):39-45.

[5] 中华人民共和国电力工业部.DL/T 620-1997交流电气装置的过电压保护与绝缘配合[S].北京:中国电力出版社,1997.

[6] 边凯,陈维江,李成榕,等.架空配电线路雷电感应过电压计算研究[J].中国电机工程学报,2012,32 (31):191-199.

BIAN Kai,CHEN Weijiang,LI Chengrong,et al.Calculation of lightning induced overvoltage on overhead distribution lines[J].Processing of the CSEE,2012,32 (31):191-199.

[7] 余占清,曾嵘,王绍安,等.配电线路雷电感应过电压仿真计算分析[J].高电压技术,2013,39(2):415-422.

YU Zhanqing,ZENG Rong,WANG Shaoan,et al.Simulation calculation and analysis of lightning induced overvoltage on power distribution lines[J].High VoltageEngineering,2013,39(2):415-422.

[8] 莫付江,陈允平,阮江军.架空输电线路雷击感应过电压耦合机理及计算方法分析[J].电网技术, 2005,29(6):72-77.

MO Fujiang,CHEN Yunping,RUAN Jiangjun.Analysis on coupling mechanism and calculation method of lightning induced surge on overhead transmission lines [J].Power System Technology,2005,29(6):72-77.

[9] 文习山,彭向阳,解广润.架空配电线路感应雷过电压的数值计算[J].中国电机工程学报,1998,18 (4):299-301.

WEN Xishan,PENG Xiangyang,XIE Guangrun.Numerical calculation of lightning-induced overvoltage of overhead distribution lines[J].Proceeding of the CSEE, 1998,18(4):299-301.

[10] 刘靖,刘明光,屈志坚,等.不同地形条件下架空配电线路的防雷分析[J].高电压技术,2011,37(4): 848-853.

LIU Jing,LIU Mingguang,QU Zhijian,et al.Comprehensive analysis of lightning performance of overhead power distribution line with varied ground obliquity [J].High Voltage Engineering,2011,37(4):848-853.

[11] 侯牧武,曾嵘,何金良.感应过电压对输电线路耐雷水平的影响[J].电网技术,2004,28(12):46-49.

HOU Muwu,ZENG Rong,HE Jinliang.Influence of lightning induced voltage on lightning withstand level of transmission lines[J].Power System Technology, 2004,28(12):46-49.

[12] PAOLONE M,RACHIDI F,BORGHETTI A,et al. Lightning electromagnetic field coupling to overhead lines:theory,numerical simulations,and experimental validation[J].IEEE Transaction on Electromagnetic Compatibility,2009,51(3):532-547.

[13] NUCCI C A,RACHIDI F,IANOZ M V,et al.Lightning-induced voltages on overhead lines[J].IEEE Transactions on Electromagnetic Compatibility,1993, 35(1):75-86.

[14] COOARY V.Some considerations on the“Cooray— Rubinstein”formulation used in deriving the horizontal electric field of lightning return strokes over finitely conducting ground[J].IEEE Transactions on Electromagnetic Compatibility,2002,44(4):560-566.

[15] RUBINSTEIN M.An approximate formula for the calculation of the horizontal electric field from lightning at close,intermediate and long range[J].IEEE Transactions on Electromagnetic Compatibility,1996,38(3): 531-535.

[16] DELFINO F,GIRDINIO P,PROCOPIO R,et al. Time-domain implementation of Cooray—Rubinstein formula via convolution integral and rational pproximation[J].IEEE Transactions on Electromagnetic Compatibility,2011,53(3):755-763.

[17] NUCCI C A,RACHIDI F,IANOZ M,et al.Comparison of two coupling models for lightning-induced overvoltage calculations[J].IEEE Transactions on Power Delivery,1995,10(1):330-336.

[18] COORAY V.Calculating lightning-induced overvoltages in power lines:a comparison of two coupling models [J].IEEE Transactions on Electromagnetic Compatibility,1994,36(3):179-182.

[19] AGRAWAL A,PRICE H,GURBAXANI S.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field[J].IEEE Transactions on Electromagnetic Compatibility,1980,22 (2):119-129.

[20] PAUL C R.Analysis of multiconductor transmission lines[M].New Jersey:John Wiley&Sons,Inc, 2008.

[21] RACHIDI F,NUCCI C A,IANOZ M,et al.Response of multi-conductor power lines to nearby lightning return stroke electromagnetic fields[J].IEEE Transactions on Power Delivery,1997,12(3):1404-1411.

[22] IEEE Std 1410TM-2010.IEEE guide for improving the lightning performance of electric power overhead distribution lines[S].New York:IEEE Power&Energy Society,2010.

(编辑 修荣荣)

Calculation model of lightning induced overvoltage using PSCAD/EMTDC program for overhead distribution lines

CHEN Jiming,ZHU Mingxiao,WANG Hui,ZHANG Zhihua
(College of Information and Control Engineering in China University of Petroleum,Qingdao 266580,China)

In order to study the lightning induced overvoltage(LIV)and lightning performance of distribution lines,the Agrawal model was converted to modal expression using the similarity transformation,and the expression was analyzed with the method of characteristics.An equivalent calculating circuit of LIV was obtained with the analysis with which a calculating model in PSCAD/EMTDC was proposed and verified for the accuracy of the model.The influences of soil resistivity,surge arrester and coupling ground wire on LIV were also analyzed.The results show that,distribution lines located in high soil resistivity region should be protected with particular emphasis;for low insulation lines,the LIV is dramatically diminished when the soil resistivity is low and arrester installation interval is less than 400 m,or the soil resistivity is high and arrester installation interval is less than 200 m;for high insulation level lines,the arrester installation interval should be less than 400 m when the soil resistivity is high;and lastly the smaller the altitude difference between line conductors and neutral conductor is,the larger the lightning induced voltages decrease.

overhead lines;lightning induced overvoltage;calculation model;soil resistivity;lightning protection

TM 863

A

1673-5005(2014)04-0192-08

10.3969/j.issn.1673-5005.2014.04.029

2013-06-03

国家自然科学基金项目(51177096);国家“863”计划(2012AA050213);中央高校基本科研业务费专项(R1305006A)

陈继明(1970-),男,副教授,博士,从事电力系统过电压防护及电力系统自动控制等研究。E-mail:jimingchen@126.com。

陈继明,朱明晓,王辉,等.基于PSCAD/EMTDC软件的配电线路感应过电压计算方法[J].中国石油大学学报:自然科学版,2014,38(4):192-199.

CHEN Jiming,ZHU Mingxiao,WANG Hui,et al.Calculation model of lightning induced overvoltage using PSCAD/EMTDC program for overhead distribution lines[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38 (4):192-199.