储层岩石T2-G实验采集参数自动匹配技术研究

吴 飞,范宜仁,邓少贵,邢东辉,刘 玺,巫振观

(1.中国石油大学地球科学与技术学院,山东青岛 266580;2.中国石油大学CNPC测井重点实验室,山东青岛 266580)

储层岩石T2-G实验采集参数自动匹配技术研究

吴 飞1,2,范宜仁1,2,邓少贵1,2,邢东辉1,2,刘 玺1,2,巫振观1

(1.中国石油大学地球科学与技术学院,山东青岛 266580;2.中国石油大学CNPC测井重点实验室,山东青岛 266580)

针对改良式CPMG(Car-Purcel-Meiboom-Gill)序列测量储层岩石内部磁场梯度分布时难以确定第一个窗口持续时间t0及回波个数NE1的问题,在总结T2-G实验采集参数人工调节规律的基础上提出t0、NE1的一项自动匹配技术:构造待测岩石的T2-G近似分布模型,基于该模型变化t0、NE1进行T2-G回波串正演数值模拟,结合T2-G最优化采集参数的约束条件确定t0、NE1。该技术在保证实验精度的前提下显著提高了实验效率,不同区块8块砂岩的T2-G实验结果也验证了该技术的可行性和实用性。

改良式CPMG序列;内部磁场梯度;采集参数;自动匹配;数值模拟

在储层岩石的内部磁场梯度作用下,扩散弛豫将加速孔隙流体的横向弛豫衰减,影响核磁共振测井解释评价的精度和流体识别效果[1-4]。获取储层岩石内部磁场梯度的大小及分布是消除或减小其对核磁共振测量影响的前提,但是岩石内部磁场梯度的影响因素复杂,无法使用公式直接计算[5-7]。Bendel等[8-11]尝试使用一维核磁共振方法定量研究岩石内部磁场梯度分布,但是应用效果不佳。二维核磁共振概念提出后,Sun和Dunn[12]设计出改良式CPMG序列,并提出相应的T2-G二维核磁共振反演方法,实现了岩石内部磁场梯度的定量表征。基于常规CPMG序列,谢然红等[13]利用不同回波间隔组合回波串的联合反演实现了T2-G二维分布计算[13]。由于改良式CPMG序列在反演速度上的优势,该序列在岩石内部磁场梯度研究中的应用越来越广泛。改良式CPMG序列第一个窗口的持续时间t0和回波个数NE1是影响T2-G实验效果的关键参数,选取不当将导致反演谱中岩石内部磁场梯度的“拖尾”现象;人工调节t0、NE1速度慢,增加了实验操作难度,亟需一种能够自动搜索和匹配t0、NE1的方法。迄今关于T2-G实验采集参数自动匹配的研究成果还未见报导,笔者在总结t0、NE1人工调节规律的基础上实现T2-G实验采集参数的自动匹配设计,并通过岩心实验考察其应用效果。

1T2-G基本原理与影响因素

图1是改良式CPMG序列示意图[12]。CPMG序列在时间轴上分为两个窗口:第一个窗口长度固定为t0,该窗口内的回波间隔从大变小;第二个窗口用仪器的最短回波间隔采集CPMG回波信号[14]。

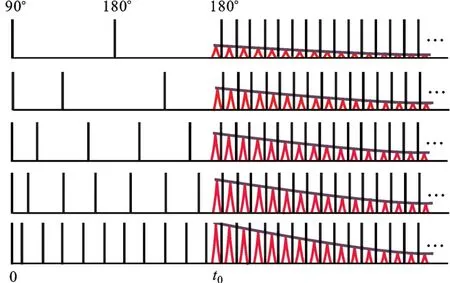
图1 改良式CPMG序列示意图[12]Fig.1 Schematic diagram of modified CPMG sequence

由多孔介质核磁共振弛豫理论,结合改良式CPMG序列的特征,可推得T2-G实验第二个窗口采集的回波串幅度[12-14]为

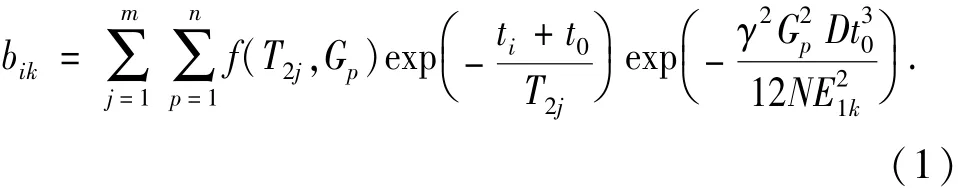
式中,bik表示第一个窗口的回波个数为NE1k时第二个窗口中第i个回波的幅度,对应的采样时间为ti+ t0,k为回波串的序号;f(T2j,Gp)为横向弛豫时间T2j、内部磁场梯度Gp对应的孔隙度分量;m为横向弛豫时间T2j分量的个数,j为序号;n为内部磁场梯度Gp分量的个数,p为序号;γ为氢核的旋磁比;D为孔隙流体的扩散系数;NE1为整数,NE1min=1,NE1max取决于核磁仪器的最小回波间隔。解谱时将T2-G实验中第二个窗口采集的多条回波串利用式(1)联立反演,即可得到储层岩石的T2-G二维分布[15-18]。

由改良式CPMG序列的测量原理及式(1)可知,T2-G测量时需根据岩石内部磁场梯度的大小和范围调节t0、NE1,实现岩石内部磁场梯度信息的有效加载。图2是N-4号砂岩不同t0、NE1对应的测量结果。实验条件:岩石饱和蒸馏水,23 MHz核磁共振岩心分析仪MR-DF,实验温度25℃。

由图2总结出t0、NE1对T2-G实验结果的影响规律:t0过小时,NE1的变化范围越小,变化NE1时回波串间的幅度差较小,实验测量易受噪声影响,导致反演谱中内部磁场梯度的分辨率降低,出现图2(a)所示的G轴“拖尾”现象;NE1组合不当时,也将导致G轴的“拖尾”现象,如图2(b)所示;手动调节t0、NE1使回波串间隔均匀,此时反演谱峰位清晰,G轴没有“拖尾”现象,如图2(c)所示。实验中人工调节t0、NE1繁琐费时,尤其是NE1的插值组合随机性强,要求操作人员有相关的核磁共振背景知识,不符合油田现场的大批量、快速测试要求。

2T2-G实验采集参数自动匹配技术

2.1 构造T2-G近似分布模型

由图2(c)N-4号饱含水砂岩的T2-G反演谱可知,储层岩石T2谱和G谱有明显的主峰,可构造T2-G二维正态分布模型作为待测岩石的近似模型;将岩石T2谱和G谱的峰值设置为构造模型的几何中心,以保证构造模型的近似程度,本文中使用长、短回波间隔CPMG序列测量的T2谱估算这两个重要参数。

长、短回波间隔测量的T2几何平均值与内部磁场梯度满足[11]:

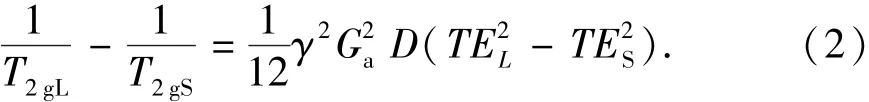
式中,T2gL为长回波间隔TEL测量的T2几何平均值;T2gS为短回波间隔TES测量的T2几何平均值;Ga为待测岩石的岩石内部磁场梯度平均值。

式(2)的假设条件:岩石中不同尺寸的孔隙对应相同的内部磁场梯度,因此式(2)计算的内部磁场梯度对应其平均值Ga。对比发现Ga与内部磁场梯度几何平均值Gg(由T2-G二维分布计算)的数量级相同,而T2gS又反映岩石T2弛豫时间的平均值,因此以(T2gS,Ga)为几何中心构造的二维正态分布模型可作为待测岩石的T2-G近似模型。

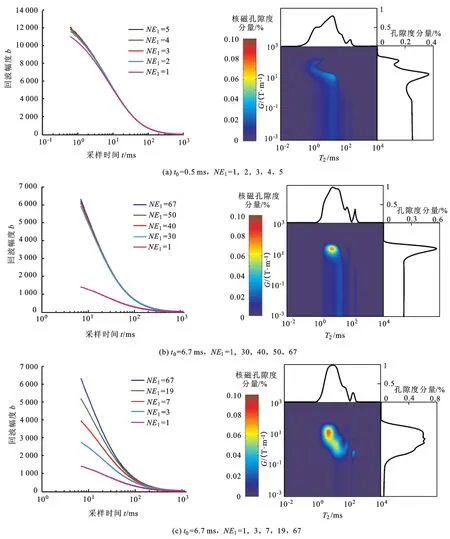
图2 N-4号砂岩不同t0、NE1对应的回波串与反演谱Fig.2 Experimental results of sample N-4 by manual changingt0andNE1

以N-4号砂岩为例,图3(a)是长、短回波间隔测量的T2谱,图3(b)是使用上述方法构造的T2-G近似分布模型f(T2j,Gp),并使f(T2j,Gp)满足归一化条件:

2.2T2-G回波串正演数学模型

T2-G实验时人工调节采集参数是根据第二个窗口的回波幅度差优选t0、NE1的,因此建立T2-G回波串正演数学模型是实现t0、NE1自动匹配的必要条件。

式(1)是改良式CPMG序列的回波幅度,写成矩阵形式[13]:

式中,B为回波幅度bik对应的矩阵;KT为T2j对应的核函数矩阵;KG为Gp对应的核函数矩阵;X为f(T2j,Gp)对应的矩阵。

核函数矩阵KT、KG由t0、NE1、TE、NE(第二个窗口)以及T2、G的布点方式计算,将构造的T2-G近似模型f(T2j,Gp)赋给X,利用式(4)即可正演模拟t0、NE1对应的回波串幅度bik。

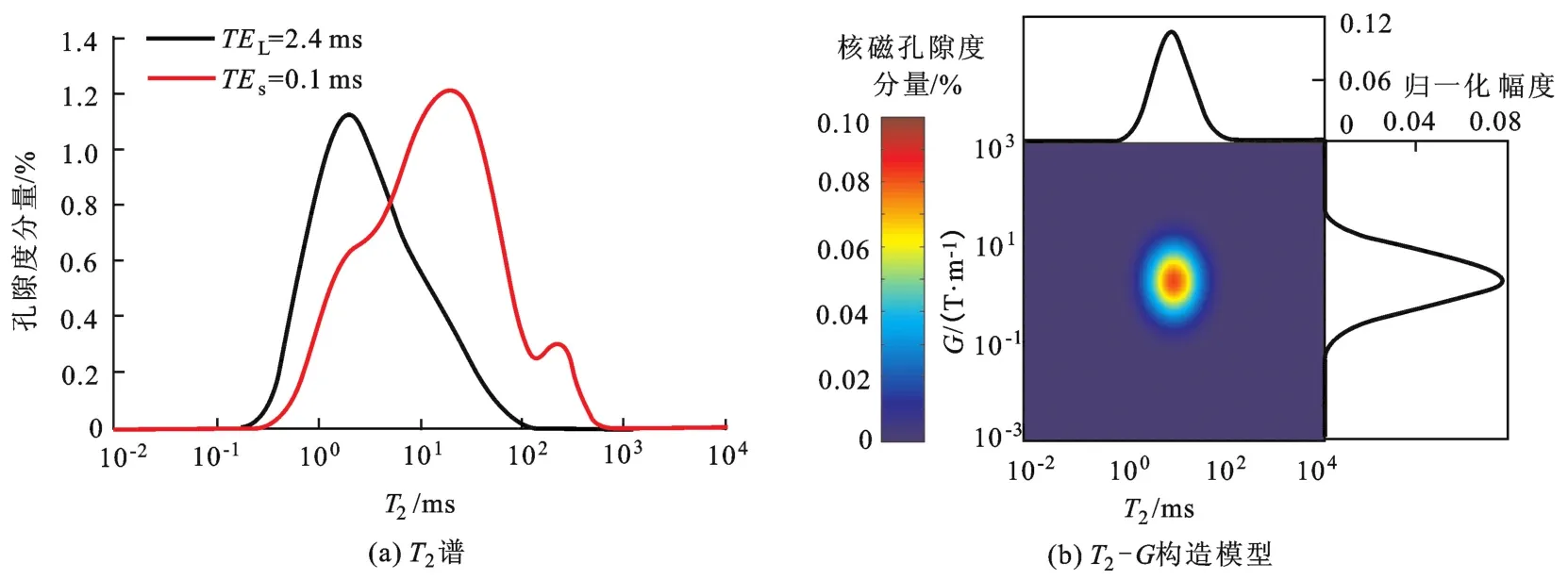
图3 N-4号砂岩T2谱及T2-G构造模型Fig.3T2spectrums and constructedT2-Gdistribution model of sample N-4

2.3t0、NE1自动匹配算法

依据t0、NE1人工调节规律,结合核磁共振岩心分析仪MR-DF的硬件参数,将最优化t0、NE1的判别条件量化,最终形成T2-G实验采集参数自动搜索和匹配算法,如图4所示。

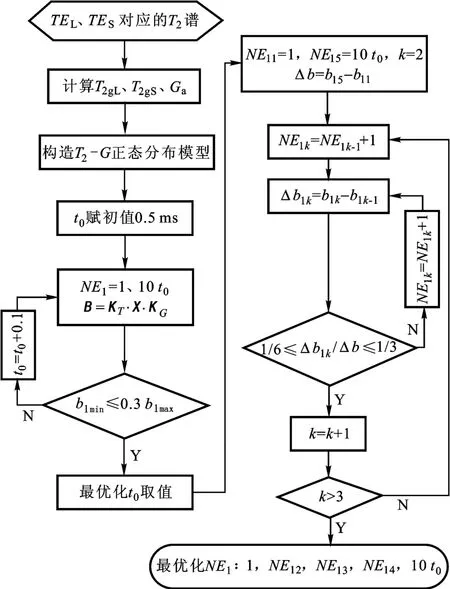
图4T2-G实验采集参数自动匹配算法Fig.4 Automatic matching algorithm for searching acquisition parameters ofT2-Gexperiment

用Matlab软件实现图4的算法,输入数据:待测岩石在长、短回波间隔下测量的T2谱,回波间隔TEL、TES;输出数据:待测岩石T2-G实验优化采集参数t0、NE1。

N-4号砂岩T2-G采集参数自动匹配结果:t0=6.4 ms,NE1=1,3,8,17,64,图5是这组参数的测量结果。构造模型只能近似表征待测岩石的T2-G分布,无法反映T2或G谱的一些细微特征,导致图5中回波串之间的间隔没有图2(c)中的均匀,但是反演谱中内部磁场梯度的分布范围和形态与图2(c)一致,说明本文中设计的t0、NE1自动匹配技术满足储层岩石的T2-G实验设计要求。

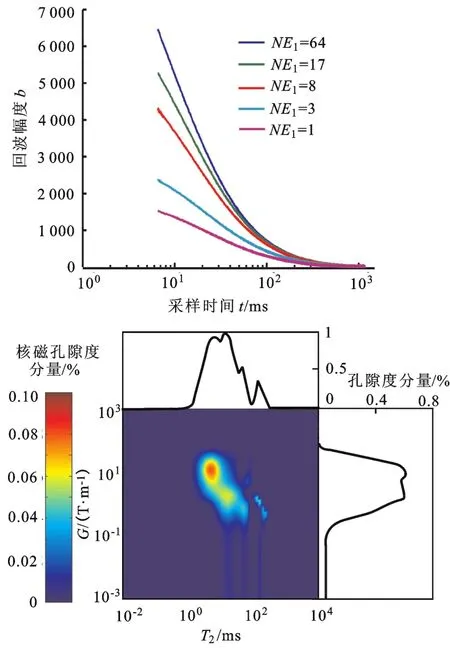
图5 N-4号砂岩自动匹配t0、NE1对应的回波串与反演谱Fig.5 Experimental results of sample N-4 by automatic matchingt0andNE1

3 应用效果分析

为检验上述T2-G实验采集参数自动匹配技术的实用性,从国内外四个不同区块选择8块不同物性的砂岩进行T2-G实验,表1是实验岩心的基础数据及t0、NE1自动匹配结果。

表1中不同区块砂岩的t0、NE1差异明显,同一区块砂岩的t0、NE1也不相同,这也印证了T2-G实验采集参数优化匹配的必要性。图6～9中给出了N-1、S-2、T-1、B-1号砂岩(对应4个不同区块)的测量结果:每块岩心回波串的幅度差明显,反演谱中峰位清晰,G轴没有“拖尾”,说明本文中设计的t0、NE1自动匹配方法能够适应不同区块、不同内部磁场梯度大小、不同物性砂岩的T2-G实验测量。

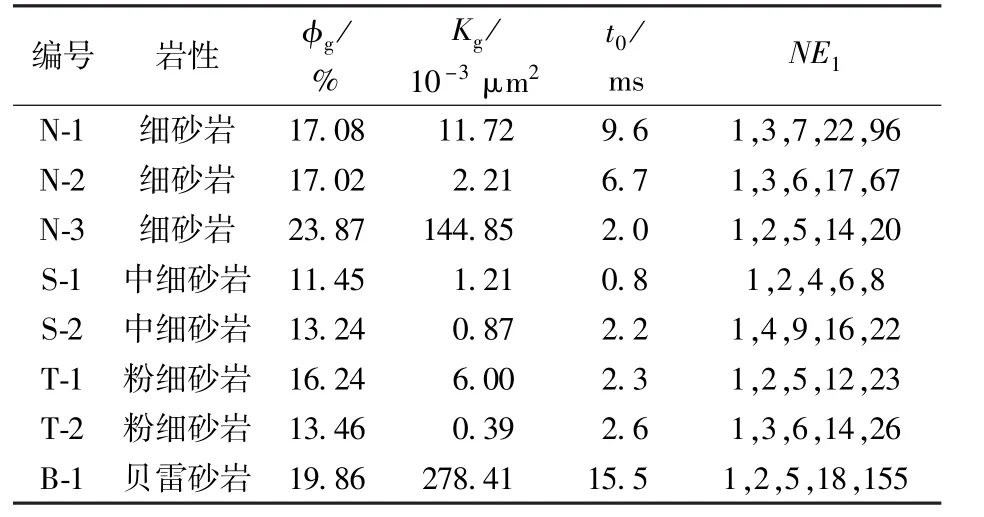
表1 实验岩心基础数据及t0、NE1自动匹配结果Table 1 Basic data and automatic matchingt0andNE1of experimental rocks

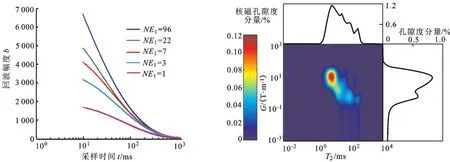
图6 N-1号岩心自动匹配t0、NE1对应的回波串与反演谱Fig.6 Experimental results of sample N-1 by automatic matchingt0andNE1

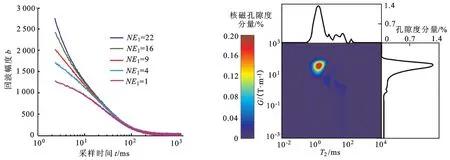
图7 S-2号岩心自动匹配t0、NE1对应的回波串与反演谱Fig.7 Experimental results of sample S-2 by automatic matchingt0andNE1

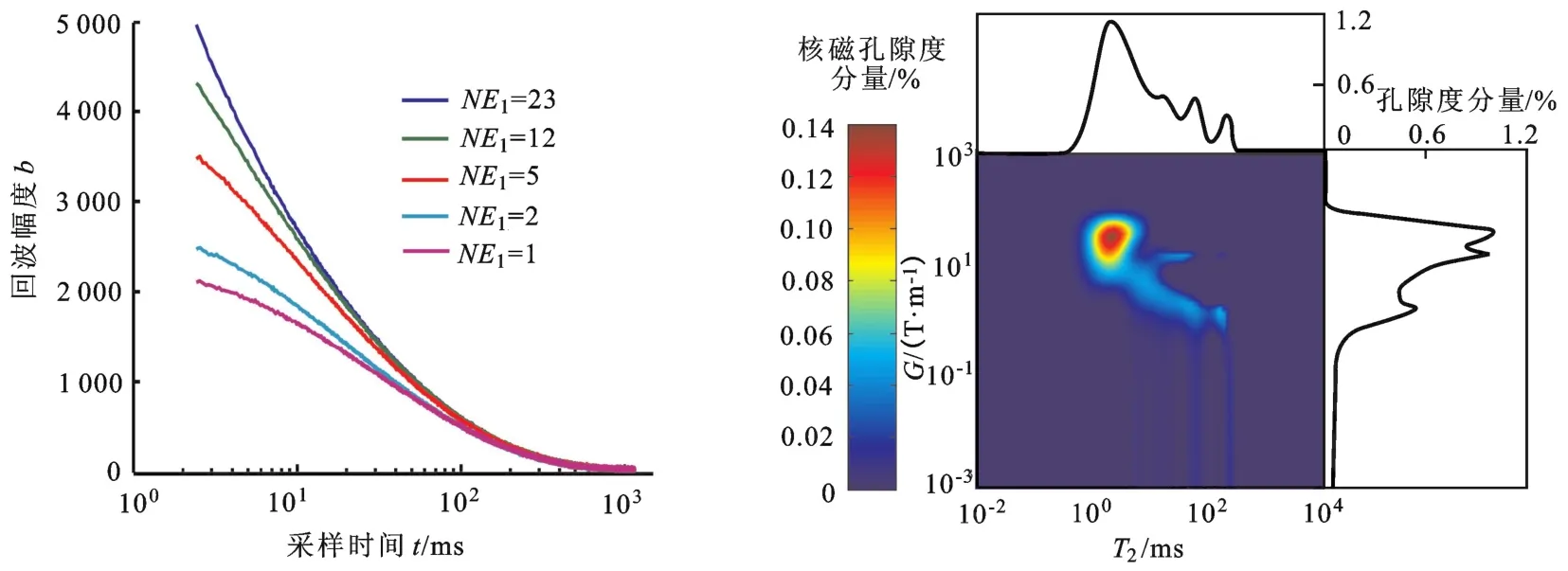
图8 T-1号岩心自动匹配t0、NE1对应的回波串与反演谱Fig.8 Experimental results of sample T-1 by automatic matchingt0andNE1

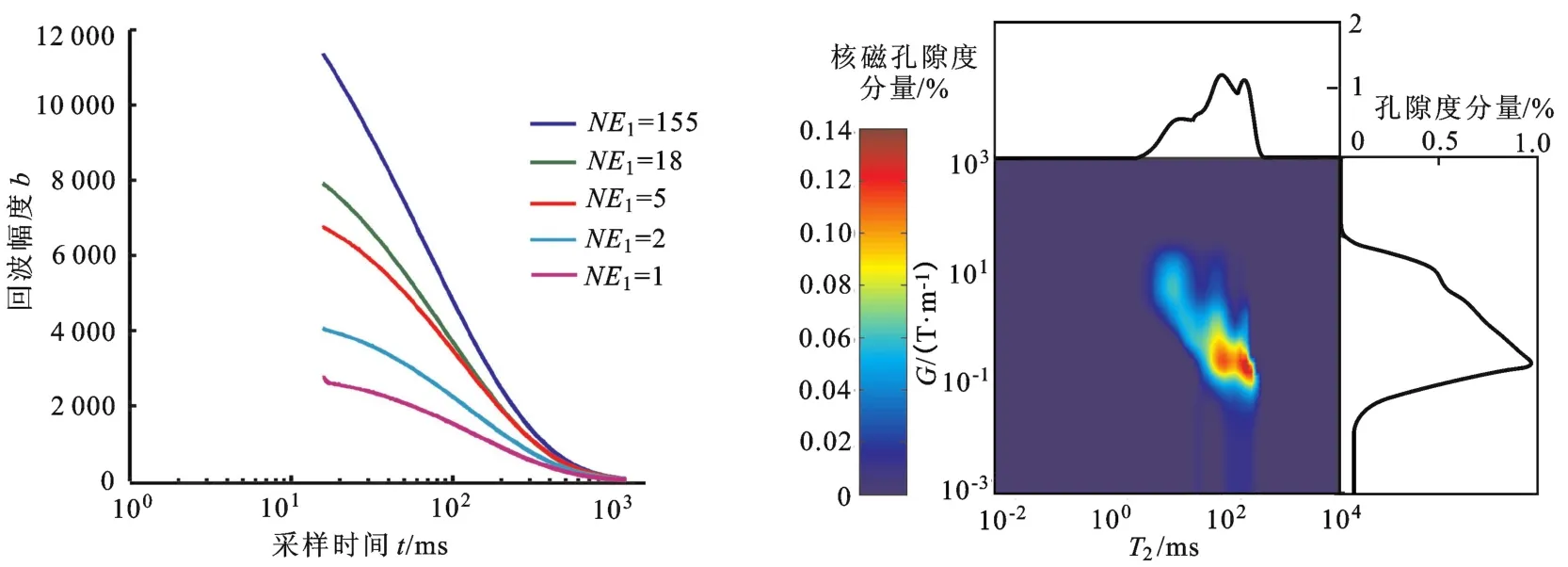
图9 B-1号岩心自动匹配t0、NE1对应的回波串与反演谱Fig.9 Experimental results of sample B-1 by automatic matchingt0andNE1

4 结 论

(1)改良式CPMG序列的t0、NE1是影响T2-G实验效果的重要参数,选取不当将导致反演谱中G轴的“拖尾”,不同地区储层岩石的内部磁场梯度差异明显,不能使用相同的t0、NE1。

(2)基于长、短回波间隔CPMG测量及T2-G回波串正演数值模拟,实现了T2-G实验采集参数的自动搜索和匹配,有效降低了实验操作难度,显著提高了实验效率;8块不同性质砂岩的T2-G实验效果验证了该技术的可行性和实用性。

(3)为进一步提高实验效率,将t0、NE1自动匹配方法集成到核磁共振岩心分析仪的采集软件,实现T2-G实验的智能采集是下一步研究方向。

[1] KLEINBERG R L,VINEGAR H J.NMR properties of reservoir fluids[J].Log Analyst,1996,37(6):20-32.

[2] DUNN K J.Enhanced transverse relaxation in porous media due to internal field gradients[J].Journal of Magnetic Resonance,2002,156(2):171-180.

[3] ZHANG G Q,HIRASAKI G J,HOUSE W V.Effect of internal field gradients on NMR measurements[J]. Petrophysics,2001,42(1):37-47.

[4] HURLIMANN M D.Effective gradients in porous media due to susceptibility differences[J].Journal of Magnetic Resonance,1998,131(2):232-240.

[5] ZHANG G Q,HIRASAKI G J,HOUSE W V.Internal field gradients in porous media:proceedings of SPWLA 41st Annual Logging Symposium,Dallas,TX[C]. Houston:The Society of Petrophysicists and Well Log Analysts,2000,paper AA.

[6] QUAN C,ANDREW E M,BRUCE G C,et al.The internal magnetic field distribution and single exponential magnetic resonance free induction decay in rocks[J]. Journal of Magnetic Resonance,2005,175(2):300-308.

[7] APPEL M,FREEMAN J J,PERKINS R B,et al.Restricted diffusion and internal field gradient:proceedings of SPWLA 40th Annual Logging Symposium,Oslo,Norway[C].Houston:The Society of Petrophysicists and Well Log Analysts,1999,paper FF.

[8] BENDEL P.Spin-echo attenuation by diffusion in nonuni-form field gradients[J].Journal of Magnetic Resonance, 1990,86(3):509-515.

[9] ZHANG G Q,HIRASAKI G J,HOUSE W V.Diffusion in internal field gradients:proceedings of International Symposium of the Society of Core Analysts[C].The Hague,Canada:Society of Core Analysts,1998,paper 23.

[10] SHAFER L S,MARDON D,GARDNER J.Diffusion effects on NMR response of oil&water in rock:impact of internal gradients:proceedings of International Symposium of the Society of Core Analysts,Golden[C]. Colorado,Canada:Society of Core Analysts,1999,paper 16.

[11] DUNN K J,APPEL M,FREEMAN J J,et al.Interpretation of restricted diffusion and internal field gradients in rock data:proceedings of SPWLA 42nd Annual Logging Symposium,Houston,TX[C].Houston:The Society of Petrophysicists and Well Log Analysts,2001,paper AAA.

[12] SUN B Q,DUNN K J.Probing the internal field gradients of porous media[J].Phys Rev E,2002,65(5): 051309.

[13] 谢然红,肖立志.核磁共振测井探测岩石内部磁场梯度的方法[J].地球物理学报,2009,52(5):1341-1347.

XIE Ranhong,XIAO Lizhi.NMR logging probing the internal magnetic field gradients of rocks[J].Chinese Journal of Geophysics(in Chinese),2009,52(5): 1341-1347.

[14] 邓克俊.核磁共振测井理论及应用[M].东营:中国石油大学出版社,2010.

[15] SUN B Q,DUNN K J.A global inversion method of multi-dimensional NMR logging[J].Journal of Magnetic Resonance,2005,172(1):152-160.

[16] VENKATARAMANNAN L,SONG Y Q,HURLIMANN M D.Solving fredholm integrals of the first kind with tensor product structure in 2 and 2.5 dimensions[J]. IEEE Trans Signal Processing,2002,50(5):1017-1026.

[17] ARNS C H,WASHBUEN K E,CALLAGHAN P T. Multidimensional inverse Laplace NMR spectroscopy in petrophysics:proceedings of SPWLA 47th Annual Logging Symposium,Veracruz,Mexico[C].Houston: The Society of Petrophysicists and Well Log Analysts, 2006,paper X.

[18] SUN B Q,DUNN K J.Core analysis with two dimensional NMR:proceedings of International Symposium of the Society of Core Analysts,Monterey,USA[C]. Houston:The Society of Petrophysicists and Well Log Analysts,2002,paper 38.

(编辑 修荣荣)

Automatic matching technology for determining acquisition parameters of formation rock T2-G experiment

WU Fei1,2,FAN Yiren1,2,DENG Shaogui1,2,XING Donghui1,2,LIU Xi1,2,WU Zhenguan1
(1.School of Geosciences in China University of Petroleum,Qingdao 266580,China; 2.CNPC Key Laboratory for Well Logging in China University of Petroleum,Qingdao 266580,China)

In order to solve the difficulties in determining the acquisition parameters such ast0andNE1when using the modified CPMG(Car-Purcel-Meiboom-Gill)sequence to measure the internal magnetic field gradient of formation rock,an automatic matching technology for determiningt0andNE1was proposed after summarizing the empirical rules applied in the field: theT2-Gapproximated distribution model of tested rocks is first constructed;then with the approximated model the response ofT2-Gexperiment is calculated by tuningt0andNE1using numerical simulation methods,and lastly the suitablet0andNE1are determined by using constraints from the optimal model.The accuracy and efficiency of the method is further verified in theT2-Gexperiment using eight sandstone samples from different regions.

modified CPMG sequence;internal magnetic field gradient;acquisition parameters;automatic matching;numerical simulation

P 631.813

A

1673-5005(2014)04-0050-07

10.3969/j.issn.1673-5005.2014.04.007

2013-12-25

“十二五”国家油气重大专项(2011ZX05020008-002);国家自然科学基金项目(41174009)

吴飞(1986-),男,博士研究生,研究方向为储层岩石物理实验方法与应用。E-mail:feizai123@126.com。

吴飞,范宜仁,邓少贵,等.储层岩石T2-G实验采集参数自动匹配技术研究[J].中国石油大学学报:自然科学版,2014,38(4):50-56.

WU Fei,FAN Yiren,DENG Shaogui,et al.Automatic matching technology for determining acquisition parameters of formation rockT2-Gexperiment[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):50-56.