一一种改进的二维MT预条件非线性共轭梯度反演方法

相 鹏

(胜利油田西部新区研究院,山东东营 257000)

一一种改进的二维MT预条件非线性共轭梯度反演方法

相 鹏

(胜利油田西部新区研究院,山东东营 257000)

在大地电磁反演方法中反演精度与计算效率问题是一对矛盾,高斯牛顿类方法反演精度高但计算效率低,非线性共轭梯度类方法计算效率高,但是反演精度不如高斯牛顿法高。在前人研究的基础上,提出一种改进的预条件非线性共轭梯度法,通过构建性状更接近高斯牛顿Hessian矩阵的预条件算子提高反演精度和计算速度。同时采用正则化参数的自适应更新算法保证反演稳定性和反演精度的平衡。模型实验验证了该方法的正确性。与其他方法的对比结果表明,该方法在保证反演精度的同时,提高了计算效率。对中国西部某地的实测MT数据进行处理解释的结果表明,该方法在解决复杂构造问题方面具有较高的实用价值。

大地电磁;预条件非线性共轭梯度;正则化参数;自适应算法;反演

近年来,大地电磁(MT)反演技术随着数值计算技术的发展已经从一维地电结构反演发展到二维、三维反演阶段。Rodi和Mackie[1]开发了非线性共轭梯度法(nonlinear conjugate gradient,简称NLCG), NLCG用单位对角阵作为预条件算子,但该预条件算子完全损失了Hessian矩阵信息。Ha和Shin[2]通过截断原始Hessian矩阵,并在每行保留大量非零元素来构建近似Hessian矩阵。这种近似Hessian矩阵用于计算高斯牛顿法的搜索方向,但是结果被假象污染,而且计算效率改善程度有限。笔者提出一种基于稀疏预条件算子的非线性共轭梯度方法(sparse preconditioned NLCG,简称SP-NLCG)。SPNLCG在近似Hessian矩阵中使用非常少的非零元素,可以保持与NLCG法几乎相同的计算开销。另外,前人研究中鲜见对正则化参数的讨论,笔者提出一种正则化参数的自适应更新算法,以保证不适应条件下反演的稳定性及最大限度提高反演结果的分辨率。

1 正演计算

对于二维地电模型,取走向为x轴,y轴与x轴垂直,z轴垂直向下(图1),介质模型的电性参数随y轴和z轴都发生变化,而沿走向x轴的电性参数不发生变化,即δ δx=0。

由于平面电磁波以任何角度入射地面都以平面波形式垂直地向下传播,将麦克斯韦方程组以x分量为准可以得到TM模式和TE模式两个独立的方程组。

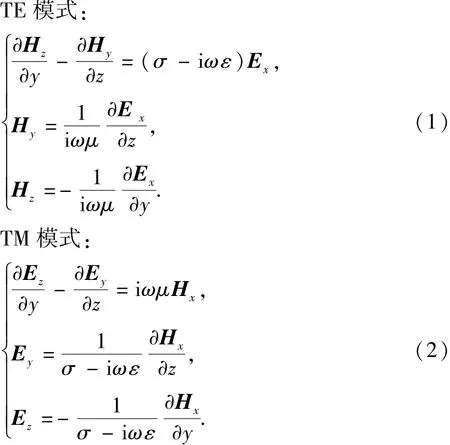
式中,E为电场强度;H为磁场强度;σ为电导率;μ为磁导率;ε为介电常数。在二维大地电磁正演计算时,边界条件是关系到解的精度的关键,TE模式外边界条件定义如下:

由于上边界AB离地面取得足够远,使异常场u在AB上为零,所以该处的u=1:

由于左右边界AD、BC与局部不均匀体距离取得足够远,电磁场在AD、BC上左右对称,其上的边界条件为

由于下边界CD以下为均质岩石,局部不均匀体的异常场在CD上为零,CD处的边界条件为

TM模式外边界条件定义如下:

(1)由于上边界AB直接取在地面上,该处的u为1:

(2)左右边界AD、BC的边界条件等于TE模式的左右边界条件。

(3)下边界CD以下的边界条件等于TE模式的边界条件。

对于TE极化模式,复数视电阻率公式为

式中,〈Ex〉为观测点电场的平均值;〈Hy〉为观测点磁场的平均值。

对于TM极化模式,复数视电阻率公式为

麦克斯韦方程可以用有限差分方程近似[3],用有限差分法求解大地电磁正演问题在一定情况下会产生伪解[4],当频率或电导率趋近于零时,传导电流场合磁场满足零散度条件,而伪解的传导电流场和磁场的散度却不为零。为了消除伪解,必须在介质和空气分别强制加入散度条件,目前常用的处理办法是强加散度校正条件:▽·E=0。

2 稀疏预条件算子非线性共轭梯度法

2.1 目标函数的构建

根据Tikhonov提出的正则化思想[5-6],大地电磁反演问题的目标函数可以用以下形式构建:

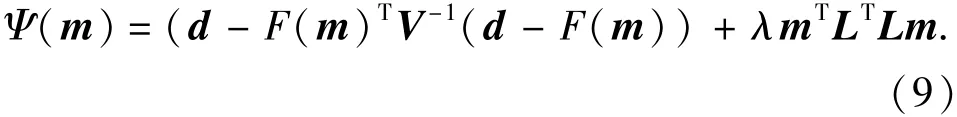
式中,d为数据矢量;m为模型矢量;正实数λ为正则化参数;正定矩阵V是数据的协方差矩阵。式(9)右边第二项是稳定因子项,很多学者对稳定因子进行了研究,如最光滑泛函[7-8]和最小梯度支撑泛函[9-11],本文中选择L为二阶差分算子实现最光滑模型约束反演。

2.2 非线性共轭梯度法

目标函数优化的常用方法有最小二乘法、高斯牛顿法、最速下降法等,这些方法都属于“牛顿型”方法,即模型的搜索方向p由下式求得:

式中,H为目标函数的二阶导数,为Hessian矩阵;g为目标函数的梯度。牛顿型方法需要计算Hessian矩阵及其逆矩阵,在求解大规模反问题时,内存需求和计算成本都非常高。Fletcher和Reeves[12]提出了NLCG法无需计算Hessian矩阵,只需计算目标函数梯度,极大地降低了对计算机内存的要求。Rodi等将其应用到MT二维反演中,并比较了高斯牛顿法、MM算法和NLCG法的性能,实验结果表明NLCG法较其他两种方法计算速度更快[1]。

NLCG的基本原理是,首先通过计算该目标函数在某参考模型处的负梯度来得到共轭梯度,并在这个方向上而不是简单的梯度方向上搜索一个最优步长使目标函数达到极小值。这样得到的解就应该是目标函数在目前共轭梯度方向的极点。其迭代计算过程可参考文献[1],NLCG与高斯牛顿法相比,最大的区别在于求取搜索方向时,不需要求取高斯牛顿Hessian矩阵并对其求逆矩阵,而是用预条件算子C代替Hessian矩阵,搜索方向的公式为

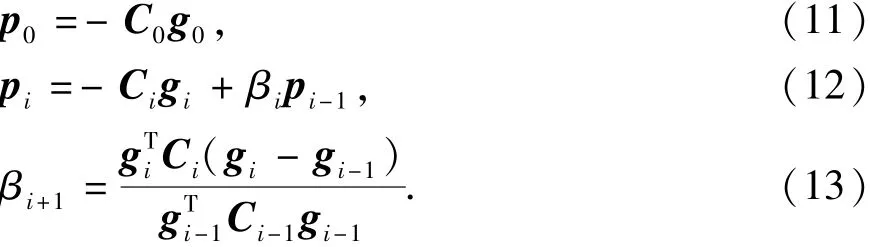
因此预条件算子C的选择对于反演的精度和收敛速度有着至关重要的作用,Rodi等给出预条件算子为Ci=(γiI+λLTL)-1,γi为特定的正实数,这种预条件算子的优点是实现简单,无需显式求解逆矩阵,但是它完全忽略掉了Hessian矩阵的信息,需要很多次迭代才能收敛至预定条件。

2.3 稀疏预条件算子

SP-NLCG的算法流程与NLCG相同,区别在于预条件算子的构建策略。预条件算子C的性状与高斯牛顿法Hessian矩阵越接近,反演的精度越高,需要的迭代次数越少。如果令式(12)中的预条件算子C等于高斯牛顿法Hessian矩阵,且去掉右边第二项,那么步长变成单位步长,SP-NLCG退化为高斯牛顿法。显然,如果C为单位矩阵,SP-NLCG变为NLCG。因此,SP-NLCG的收敛速率应该介于NLCG和高斯牛顿法之间。

构建预条件算子的主要挑战在于如何设计近似Hessian矩阵,使之有效且计算廉价。出于效率的考虑,近似Hessian矩阵必须高度稀疏同时保持精度。为了得到高度稀疏的近似Hessian矩阵,选择高斯牛顿Hessian矩阵中最主要的元素,舍弃贡献小的元素。Hessian矩阵的每个元素是雅可比矩阵两列的内积,而雅可比矩阵的每一列代表观测矢量对离散化的反演区域中某个网格的模型参数的梯度。实验表明,当模型网格在空间上接近,则对应的雅可比矩阵列向量有很强的相关性。最强的相关性为自相关。这些空间接近的网格产生了Hessian矩阵中的主控元素。因此,在构建高度稀疏Hessian矩阵的第i行时,只要选择包围着对应雅可比矩阵第i列的网格的那些网格的雅可比列向量即可。选择的雅可比列向量不必是邻近的,虽然它们对应的网格在空间上是邻近的。

稀疏近似Hessian矩阵的结构如图2(a)所示。

对角线元素是雅可比矩阵列向量的自相关,对应圆圈区域的中心网格,而副对角线元素是圆形区域中不同网格的互相关。称图2(b)的圆形为Hessian圆,该圆仅包括4个相邻网格(二维), Hessian圆越大,近似Hessian矩阵的稀疏性越差。数值模拟表明在近似Hessian矩阵中包含更多非零项超过一定界限时,不会使高斯牛顿Hessian矩阵的近似逆矩阵的精度提高更多。实际上,在多数情况下精度会变差。

传统的Hessian矩阵近似方法中,当构建第i行时,只考虑雅可比矩阵第i列的自相关和第i列与相邻几列的互相关。传统Hessian近似矩阵的结构如图3(a)所示。对角线元素是图3(b)中矩形区域中心网格的自相关,副对角线元素是中心网格与其他相邻网格的互相关。对比图2(b)和图3(b),认为图2(b)的近似Hessian矩阵更精确,因为它包括了最重要的元素,而且还包括了z方向的互相关,在传统近似方法中该信息被忽略。Ha和Shin[2]在构建Hessian近似矩阵时需要上百个非零元素,SPNLCG在对搜索方向步长进行优化后,仅需要5个非零元素。

与NLCG相比SP-NLCG唯一额外的运算是求解式(12)左边第一项,令Cigi=,因为近似Hessian矩阵的高度稀疏性,采用了LU分解直接求解近似Hessian矩阵的逆矩阵。采用稀疏预条件算子SP-NLCG的效率与NLCG相当,但是性能却得到明显改善。

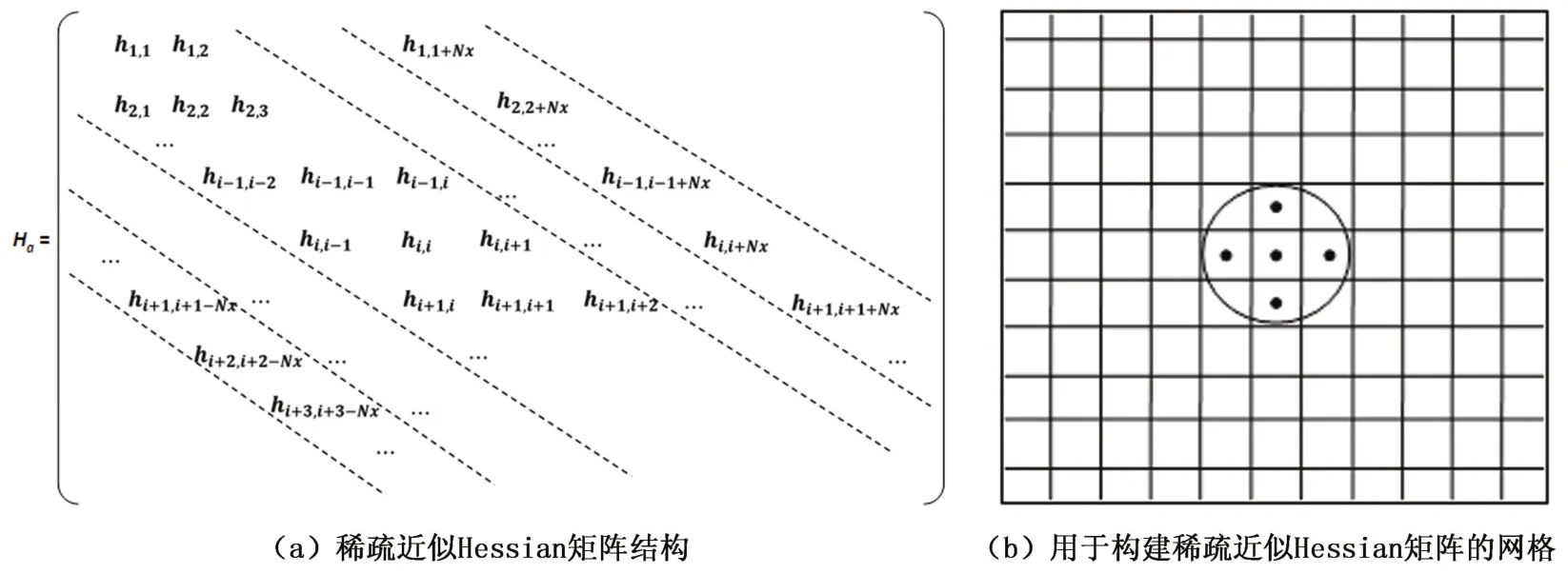
图2 稀疏近似Hessian矩阵结构及其构建网格示意图Fig.2 Structure of sparse approximate Hessian matrix and its diagram of inversion grids constructing matrix

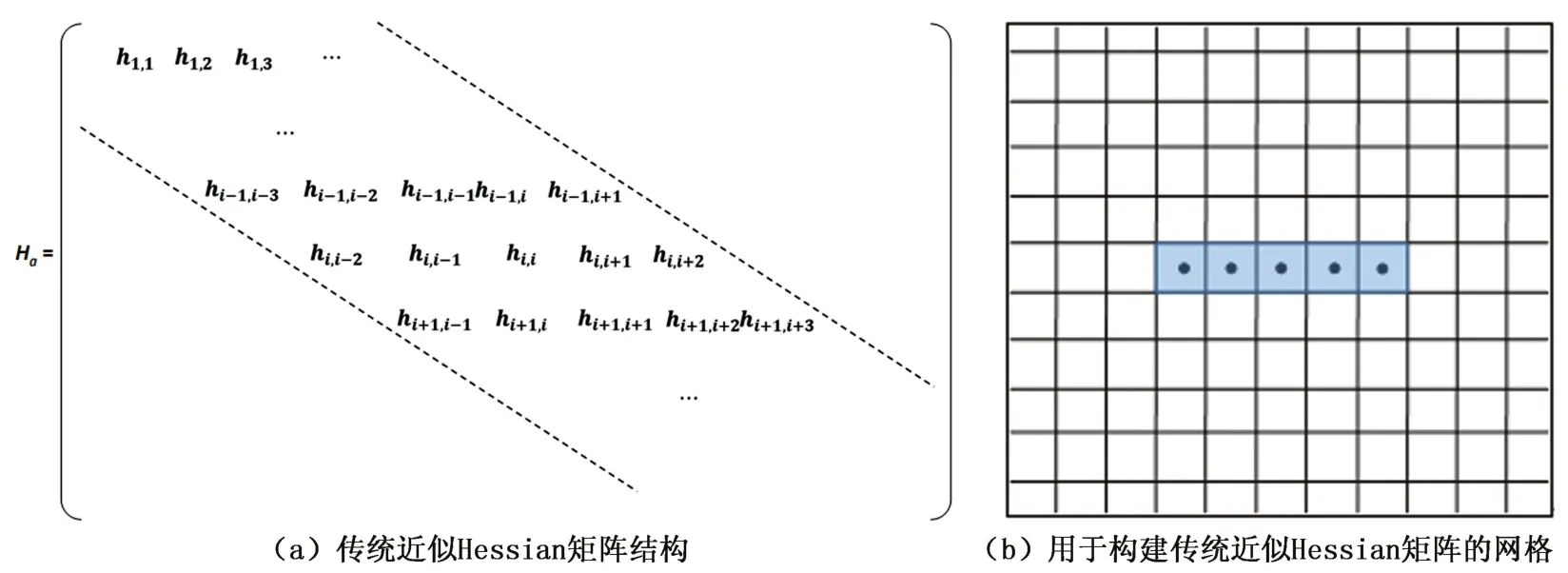
图3 传统近似Hessian矩阵结构及其构建网格示意图Fig.3 Structure of traditional approximate Hessian matrix and its diagram of inversion grids constructing matrix

2.4 正则化参数自适应更新方法

Rodi等[1]的研究中对正则化参数λ没有进行讨论,只是将其固定为一个正实数,当预条件算子为Ci=(γiI+λLTL)-1时,因为γi是一个正实数,LTL是对称正定矩阵,所以C总是可逆,λ的作用仅为控制模型的平滑度,λ越大求得的模型越平滑。然而当用稀疏近似Hessian矩阵代替预条件算子的单位矩阵时,γiH不一定可逆,需要λLTL项改善矩阵的条件数,若λ过大则降低了模型的分辨率且增加迭代次数,若λ过小,则γiH+λLTL不可逆,导致计算失败。因此,理想的方案是在迭代过程中自适应修改λ,既能保持模型的分辨率,又能保证算法的稳定性和计算效率。

本文中采用的自适应更新正则化参数λ的方法如下:选择正则化因子序列λ0＞λ1＞＞λ2＞…＞＞λl,其中λ0要足够大而λl要足够小,在反演过程中根据每次迭代情况从序列中选择下次迭代的正则化参数。正则化参数序列可以用下式计算:λk=λ0qk,k=1,2,…,l;q＜0。

正则化参数自适应更新算法的计算流程如下:

(1)计算当前模型的目标函数中的稳定因子项s(mn);

(2)令ζ=s(mn)/s(mn-1);

(3)如果ζ≤1,则λn+1=λn,如果ζ＞1,则λn+1=λn/ζ;

(4)如果当前迭代的数据残差rn减小不够快, 即0.01,更新正则化参数

λ′n+1=qλn+1,衰减系数q通常在区间[0.5,0.9]上选取。

正则化参数的初始值λ0计算公式为

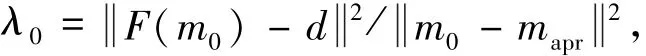
式中,mapr为先验模型;m0为初始模型;F为正演算子。通过自适应算法,实现了反演精度和计算稳定性之间的平衡。

3 数值实验

3.1 块体组合模型

图4(a)所示模型与文献[7]中模型相同,均匀半空间中嵌入两个矩形异常体,异常体的电阻率分别为5和2000 Ω·m,背景电阻率为100 Ω·m,用此模型生成模拟数据。观测点11个,间距10 km,频点16个,频率范围为0.001～100 Hz。

用该简单模型对比分析SP-NLCG法与OCCAM法、NLCG法之间的差异。图4(b)～(d)是不同方法的反演结果。使用TE和TM数据进行联合反演,参数为正则化参数初值λ0=100 000,SP -NLCG的正则化参数衰减系数q=0.7,均方根误差阈值设为1.3。反演剖面两侧与底部的不均匀网格是为了减小边界效应所扩充的网格。

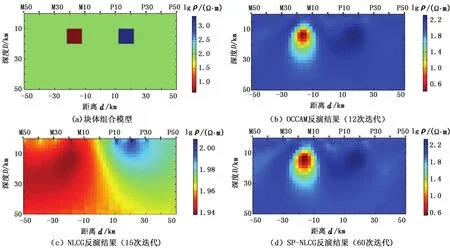
图4 块体组合模型实验结果Fig.4 Block model test results

图4(b)是OCCAM法反演结果,OCCAM法实质上是正则化的高斯牛顿法,本实验中用其反演结果作为标准与其他方法的反演结果进行对比。图4(c)为NLCG反演结果,预条件算子为Ci=(γiI+ λLTL)-2,没有使用Hessian矩阵中的元素作为预条件算子,并且在迭代过程中不更新正则化参数λ。反演进行了15次迭代后因为不能再降低均方根误差而终止,此时均方根误差为3.17。这是因为正则化参数初值过大,且该值在反演过程中保持不变,导致反演结果过于平滑,分辨率较低。图4(d)是采用SP-NLCG的反演结果,预条件算子为Ci=(γiH+ λiLTL)-2,Hessian圆半径为1,其效果与OCCAM法相当,不同之处在于(d)的模型较(b)的粗糙度稍大一些,这是由于两种方法对正则化参数的更新策略不同所导致的,OCCAM法在每次迭代中为了寻找最优的正则化参数要进行多次正演计算,在本实验中每次迭代需要6～8次正演计算寻优正则化参数,从而导致计算量大幅度增加。本文中采用的正则化参数更新算法不需要额外的正演计算,尽管SP -NLCG达到收敛所需的迭代次数(60次)多于OCCAM法(12次),但耗时却比OCCAM法少。

本实验模型非常简单,采用不同Hessian圆半径的反演结果都非常接近。图5为不同反演方法迭代误差曲线,从图中可以看出OCCAM法收敛速率最快,因此它需要的迭代次数最少。SP-NLCG最终也收敛到误差阈值,当Hessian圆半径为0时,即预条件算子仅取Hessian矩阵对角线元素,所需迭代次数大于Hessian圆半径不为0时的迭代次数。当Hessian圆半径为1时,比半径为3和5时所需迭代次数少,计算速度最快。说明对于SP-NLCG,预条件算子中包含Hessian矩阵元素并非越多越好,本实验以及后续实验证明当Hessian圆半径为1,即预条件算子每行包含5个Hessian矩阵元素时,反演性能最优。

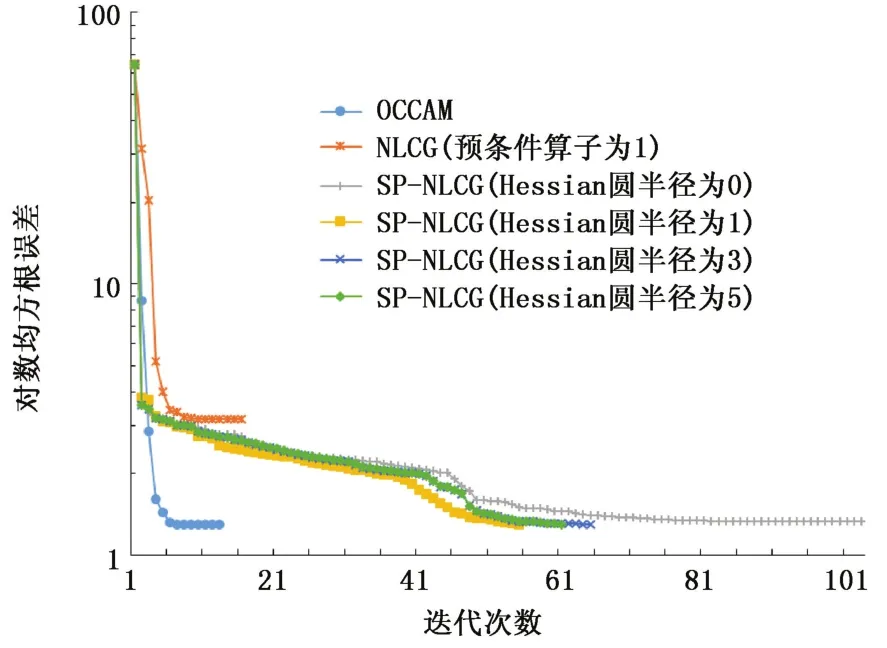
图5 块体组合模型反演误差曲线Fig.5 RMS curves of block model test

3.2 推覆逆掩模型实验

为了测试SP-NLCG法对复杂构造的适用性,设计一个推覆逆掩模型(图6(a))。该模型的右侧为沉积地层,电阻率从浅到深分别为100、30、100、400 Ω· m的老地层逆掩在新地层之上。观测点34个,间距1 km,频点数为38,频率范围为0.001～320 Hz。

图6(b)～(e)是不同方法的反演结果,使用TE和TM数据进行联合反演,正则化参数初值λ0= 100000,SP-NLCG的正则化参数衰减系数q=0.7,均方根误差阈值设为1.3。

图6(c)为NLCG反演结果,反演进行了14次迭代后因为不能再降低均方根误差而终止,此时均方跟误差为5.69。与图6(b)的OCCAM法反演结果相比,反演精度明显要低很多,与图6(d)所示的Hessian圆半径为1的SP-NLCG的15次迭代结果相比,其精度也低很多。原因有两方面:①预条件算子中不包含任何Hessian矩阵元素,损失大量有效信息,降低了反演分辨率;②反演迭代过程中不更新正则化参数,过大的正则化参数初值使得模型过于平滑,后期迭代已经不能再降低均方根误差,导致反演不能达到规定阈值而提前结束。

图6(e)为Hessian圆半径为1的SP-NLCG的36次迭代结果,其精度与OCCAM法反演结果相当,很好地恢复出了逆掩构造和沉积地层。Hessian半径取不同值时的反演结果都比较接近,但计算效率存在较大差异,图7给出了不同反演方法迭代误差曲线。

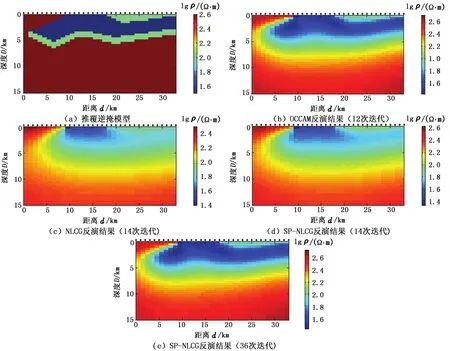
图6 推覆逆掩模型实验结果Fig.6 Overthrust model test results

从图7和表1中可以看出SP-NLCG的收敛速度介于OCCAM法和NLCG法之间,当Hessian圆半径为0时,反演所需45次迭代达到误差阈值, Hessian圆半径为5时,需要40次迭代,Hessian圆半径为1和3时,分别需要36次和35次迭代,尽管Hessian圆半径为1时的迭代次数比Hessian圆半径为3时迭代次数要多一次,然而从表1中可以看到其计算时间却是最短的,这是因为预条件算子包含的非零元素越多,对其进行求逆运算所需的时间越长。

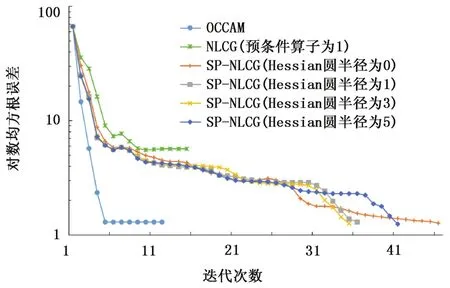
图7 推覆逆掩模型反演误差曲线Fig.7 RMS curves of overthrust model test

图8是SP-NLCG法在Hessian圆选取不同半径时预条件算子包含的Hessian矩阵元素,其中图8(a)是完整的Hessian矩阵,图8(b)～(d)分别是Hessian圆半径为0、1、3时的近似Hessian矩阵。从图中可以看出近似Hessian矩阵都为高度稀疏的对角阵,元素集中在主副对角线上,元素个数比完整Hessian矩阵少很多,因此在求预条件算子时无论是计算量还是对内存的要求都不高。

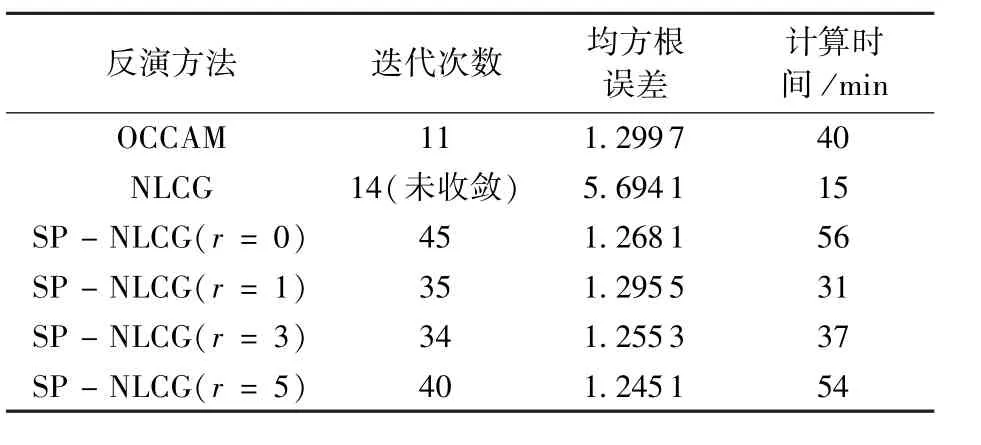
表1 不同反演方法性能参数对比Table 1 Performance parameters of different inversion methods

图8 Hessian矩阵对比Fig.8 Hessian matrix comparison

4 实测资料处理

为了检验本文研究方法处理实测数据的有效性,对中国西部某地的实测MT数据进行反演。该地区属于山前构造带,第四系为不稳定中高电阻层;第三系到白垩系为低阻层,电阻率为几欧姆米;侏罗系为次低阻层,电阻率一般小于30 Ω·m;三叠系为次高阻层,电阻率在30～100 Ω·m范围变化;石炭系则基本是高阻,超过100欧姆甚至达上千欧姆米,也有部分上石炭统电阻率不到100 Ω·m。

图9上图为MT 2维连续介质反演剖面,剖面总长60 km,观测点120个,观测点距500 m,观测数据频点数为38,频率范围为0.001～320 Hz。剖面能较清晰地反映沉积盆地的基本构造形态,但是对深部构造的恢复不理想,出现了许多不自然的“挂面条”现象,难以刻画深层的盆山接触关系。剖面中下部偏左处的相对低阻隐约反映出存在逆掩构造,但是该构造在地震偏移剖面(图9下图)很难识别,因此很难确定该构造的存在。

图10为SP-NLCG法反演得到的电阻率剖面和电震联合解释剖面。可以看出,该剖面对沉积地层的形态刻画清晰,且恢复出了深层的逆掩构造。最上面的低阻地层为大面积出露地表的第四系-白垩系,从左到右逐渐变薄,最右边厚度为1800 m;第二层为侏罗系-三叠系的相对中高阻层,被石炭系高阻推覆体冲断成东西两段,厚度约2 600 m;第三层和第四层分别为上二叠统的中低阻层和下二叠统的中高阻层,这两层都被逆冲断层划成3段,第五层为石炭系的高阻层,在测线最右边有出露,剖面中部为大套的高阻层,并未发育低阻层,根据地震偏移剖面解释为石炭和二叠地层。利用本文方法的反演结果指导了该地区构造解释,尤其是对深层部位石炭系和二叠系的刻画较为精准,证实了SP-NLCG法解决中国西部复杂构造问题的有效性。

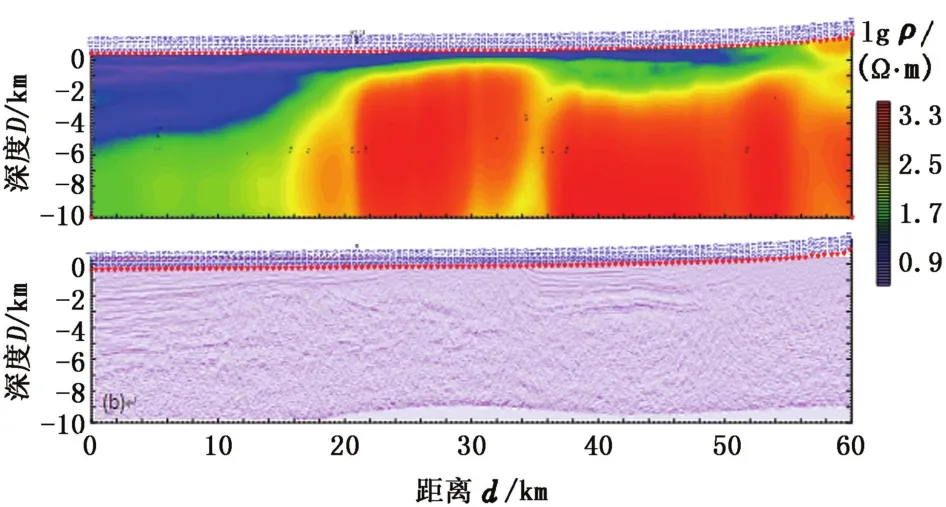
图9 MT 2维连续介质反演剖面与地震偏移剖面Fig.9 MT 2D continuous inversion result and seismic migration profile

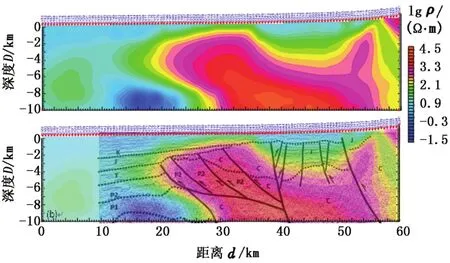
图10 预条件非线性共轭梯度法反演剖面与电震联合解释剖面Fig.10 Inversion results of SP-NLCG and MT&seismic co-interpretive profile

5 结 论

(1)通过分析雅克比矩阵中列向量的自相关和互相关,发现构建近似Hessian矩阵最有效的模式是仅使用以某网格为中心的Hessian圆内的网格所对应的雅克比矩阵列向量。数值实验证明该方法的反演结果精度比非线性共轭梯度法精度更高,与高斯牛顿法相当,且计算速度比高斯牛顿法快,与非线性共轭梯度法相当,在通常情况下Hessian圆半径为1时反演性能最优化。

(2)通过引入正则化参数的自适应更新算法,在迭代过程中自适应修改λ,既能保持模型的分辨率,又能保证算法的稳定性和计算效率。

[1] RODI W,MACKIE R.Nonlinear conjugate gradients algorithm for 2D magnetotelluric inversion[J].Geophysics,2001,66:174-187.

[2] HA T,SHIN C.Problems of constructing the approximate Hessian in waveform inversion[J].SEG Technical Program Expanded Abstracts,2002,21:961-962.

[3] MACKIE R L,BENNET B R,MADDEN T R.Long-period magnetotelluric measurements near the central California coast:a land-locked view of conductivity structure under the Pacific Ocean[J].Geophysical Journal International,1988,95:181-194.

[4] 金建铭,王建国.电磁场有限元方法[M].西安:西安电子科技大学出版社,1998.

[5] TIKHONOV.Solution of incorrectly formulated problems and the regularization method[J].Soviet Math,1963,4: 1035-1038.

[6] TIKHONOV.Regularization of incorrectly posed problems [J].Soviet Math,1963,4:1624-1627.

[7] CONSTABLE S C,PARKER R L,CONSTABLE C G. Occam's inversion:a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics,1987,52:289-300.

[8] DEGROOT HEDLIN C,CONSTABLE S.Occam's inversion to generate smooth,two-dimensional models from magnetotelluric data[J].Geophysics,1990,55(12): 1613-1624.

[9] PORTNIAGUINE O,ZHDANOV M S.Focusing geophysical inversion images[J].Geophysics,1999,64:874-887.

[10] PORTNIAGUINE O,ZHDANOV M S.3-D magnetic inversion with data compression and image focusing[J]. Geophysics,2002,67(5):1532-1541.

[11] ZHDANOV M S,ELLIS R,MUKHERJEE S.Three-D regularized focusing inversion of gravity gradient tensor data[J].Geophysics,2004,69:925-937.

[12] FLETCHER R,REEVES C M.Function minimization by conjugate gradients[J].Computer J,1959,7:149-154.

(编辑 修荣荣)

Two-dimensional MT inversion method based on an improved preconditioned nonlinear conjugate gradient algorithm

XIANG Peng
(Research Institute of New District in West China,Shengli Oilfield,Dongying 257000,China)

Accuracy and computational efficiency are conflicting to each other in MT inversion methods.Gauss-Newton methods have high accuracy but poor efficiency,while nonlinear conjugate gradient methods are computationally efficient but less accurate.A new preconditioned nonlinear conjugate gradient method is proposed to improve both accuracy and computational cost by using a precondition operator whose performance is approximated by Gauss-Newton Hessian matrix.A self-adapted algorithm updating the regularization parameter is used to guarantee the balance between the stability and the accuracy of the inversion.Through the model tests and comparisons with other methods,the proposed method is proved achieving the goal. The method is applied to invert the MT data measured from a region in west China.The inverted resistivity profile is conjointly interpreted with seismic migration profile,and illustrates its significance in complicated structural interpretation.

magnetotelluric(MT);preconditioned nonlinear conjugate gradient(PNLCG);regularization parameter;self-adapted algorithm;inversion

P 631.3

A

1673-5005(2014)04-0042-08

10.3969/j.issn.1673-5005.2014.04.006

2013-12-19

国家科技重大专项(2011ZX05002-002)

相鹏(1978-),男,工程师,博士,主要从事地球物理正反演方法研究。E-mail:ddzk@163.com。

相鹏.一种改进的二维MT预条件非线性共轭梯度反演方法[J].中国石油大学学报:自然科学版,2014, 38(4):42-49.

XIANG Peng.Two-dimensional MT inversion method based on an improved preconditioned nonlinear conjugate gradient algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):42-49.