基于旋量理论的滚仰式导引头跟踪指令解算

刘 凯，梁晓庚，李友年

(中国空空导弹研究院，河南 洛阳 471000)

导引头是自动寻的导弹的关键组成部分，导引头的性能对导弹的作战性能具有重大的影响。为了适应现代战争的需要，新一代近距格斗空空导弹应具有高机动性及大离轴角发射能力，要求导引头视场大、体积小、质量轻。传统的导引头稳定平台采用速率陀螺稳定平台，难以满足现代战争的要求。滚仰式导引头既减小了导引头的质量和体积，又节约成本，是新一代空空导弹稳定平台的理想选择。

滚仰导引头对应的探测器光轴运动方式是以弹体纵轴为轴线的空间圆锥运动，因此，像点在像平面上按照极坐标描述。采用这种结构形式，滚转和俯仰回路会产生指令多值问题。传统的角增量解算方法采用运动学关系分别计算光轴和视线方向单位矢量在弹体坐标系的投影，由两矢量的恒等关系求解出跟踪指令。这种方法通常只能求解出解空间中的一个解，在跟踪过程中会出现数值解频繁在不同解之间跳动的问题，导致目标丢失。

为解决这个问题，本文提出了基于旋量理论的求解滚仰导引头跟踪指令的方法。本文分析了滚仰式导引头的运动学关系，将求解光轴与视线重合的逆运动学问题分解为Paden-Kahan 子问题，求解相应的Paden-Kahan 子问题来得到所有的运动学逆解。为避免数值解在解空间中频繁跳动的问题，采用最小增量角准则对运动学逆解进行优化，给出平滑连续的角跟踪指令。

1 滚仰导引头角跟踪指令计算

1.1 滚仰导引头跟踪原理

导引头的运动学关系可以考虑为由滚转轴和俯仰轴组成的开运动学链。在滚转俯仰轴线相交点建立如图1 所示的5 个坐标系。其中，ox0y0z0为弹体坐标系;ox1y1z1为滚转坐标系，与滚转轴固联，ox1轴与滚转轴重合，γ 为滚转角;ox2y2z2为俯仰坐标系(光轴坐标系)，与俯仰轴固联，oz2轴与俯仰轴重合，ox2与光轴重合，θ 为俯仰角。跟踪过程中，光轴坐标系ox2y2z2的指向和视线之间存在失调角εy和εz，将ox2y2z2绕oy2旋转εy形成坐标系ox3y3z3，ox3y3z3绕oz3旋转εz形成坐标系ox4y4z4(视线坐标系)。ox4的指向即为视线方向。

图1 滚仰导引头运动学关系

滚仰式导引头跟踪过程如下:导引头探测器根据目标及导引头的位置信息得到目标误差角εy和εz，结合此时导引头俯仰、滚转框架角γ 和θ，解算导引头的跟踪指令Δγ 和Δθ，经过校正及功放，分别输送给两通道得力矩电机，通过电机转动使导引头指向目标，完成导引头的跟踪闭环控制。

1.2 滚仰导引头角跟踪指令计算方法

滚仰导引头的角跟踪指令算法是将台体坐标系中目标的方位误差和俯仰误差分解到俯仰电机轴和横滚电机轴，即将目标偏差信号εy和εz换算成应有的横滚控制角γs和俯仰控制角θs，从而通过控制横滚转动和俯仰转动达到跟踪目标的目的。

两轴跟踪是通过两种不同的坐标变换得到目标视线矢量。第一种变换，根据当前的框架角γ 和θ 将弹体系换到内环台体坐标系，在通过失调角εy和εz，使得光轴对准目标矢量;第二种变换，将弹体系通过应有的控制角γs( γ+Δγ)和θs( θ+Δθ)直接变换到视线坐标系，其中Δγ 和Δθ 是横滚框架角增量和俯仰角增量，比较两个视线矢量即可计算得到Δγ 和Δθ。

经推到计算可得

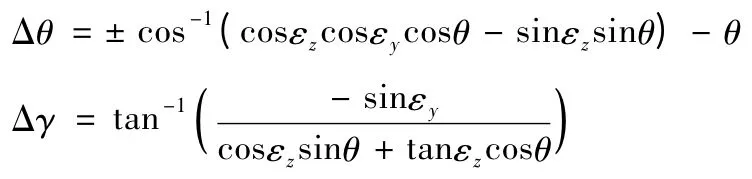
由上述两式可以看出，滚仰导引头的角增量指令是通过三角函数来解算的，所以存在多值性。由此，本文提出基于旋量理论和Paden-Kahan 子问题求解滚仰导引头跟踪指令的方法来消除三角函数带来的多值性。

2 Paden-Kahan 子问题

2.1 Paden-Kahan 子问题1-绕单轴旋转

设ξ 为一零节距轴线，p，q∈R3为空间两点，求旋转角θ使其满足

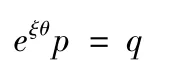
假设r 为旋转轴ξ 上的一点，定义u=p-r 为从r 到p 的矢量，v=p-r 为从r 到q 的矢量，如图2 所示。

图2 Paden-Kahan 子问题1

由恒等式eξθr=r 可得

其中ω∈R3为轴线ξ 方向的单位矢量。

定义u'和v'分别为矢量u 和v 在与轴线垂直平面的投影。由几何关系可得:

上式有解的充要条件为

当满足上述关系时，可得

2.2 Paden-Kahan 子问题2-绕双轴旋转

设ξ1和ξ2为相交于一点的两条零节距轴线，p，q∈R3为空间两点，求旋转角θ1和θ2使其满足

子问题2 相当于空间点p 先绕轴线ξ2旋转θ2，再绕轴线ξ1旋转θ1，与空间点q 重合，如图3。当轴线ξ1和ξ2重合时，子问题2 退化为子问题1。

图3 Paden-Kahan 子问题2

假设两轴线不重合，r 为两轴的交点，空间中存在点c，满足

可描述为向量形式:

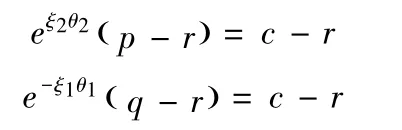
定义向量u=p-r，z=p-r，v =p-r，ω1和ω2分别为ξ1和ξ2方向上的单位矢量。

可描述为

即向量满足:

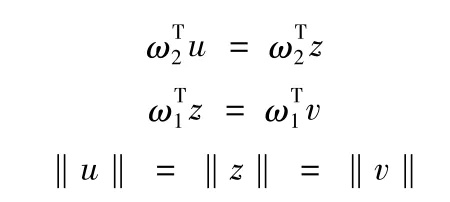
由于ω1，ω2和ω1×ω2线性独立，可得

将式带入式和式，可得

求解式可得

由式可解的z，进而求解c。分别应用子问题1 就可以求解θ1和θ2。

3 跟踪仿真

为了验证算法的有效性，建立滚仰导引头机动目标跟踪仿真实验闭环系统，仿真原理如图4。

图4 跟踪仿真原理

假设弹体不动，弹体坐标系与惯性坐标系重合，初始的框架角均为0。由于假设弹体不动，则可以忽略弹体扰动对视线的影响，所以只需要保留位置回路。

假设目标在惯性空间的运动为圆周运动，跟踪结果如图5、图6 所示。结果表明，提出的跟踪角指令算法是可行的，并且能够保证有效跟踪机动目标。

图5 方位失调角

图6 俯仰失调角

5 结束语

本文提出一种基于Paden-Kahan 子问题的滚仰式导引头跟踪指令求解算法。将求解滚仰导引头跟踪指令的运动学问题分解为Paden-Kahan 子问题，从而得到所有的运动学逆解。为避免数值解在解空间中的多值问题，采用最小增量角准则对滚仰跟踪指令进行优化。对圆周轨迹目标进行仿真跟踪实验，试验结果表明，该算法能够有效的跟踪机动目标。

［1］王志伟，祁载康，王江.滚-仰式导引头跟踪原理［J］.红外与激光工程，2008，37(2):274-277.

［2］樊会涛，刘代军. 红外近距离格斗空空导弹发展展望［J］.红外与激光工程，2005，34(5):564- 568.

［3］姚郁，章国江.捷联成像制导系统的若干问题探讨［J］.红外与激光工程，2006，35(1):1- 6.

［4］RUDIN R T. Strapdown stabilization for imaging seekers［R］.AIAA-93-2660，1993.

［5］钱东海，王新峰，赵伟，等.基于旋量理论和Paden-Kahan子问题的6 自由度机器人逆解算法［J］.机械工程学报，2009，45(9):72-81.

［6］理查德.摩恩，夏思卡萨思特里，等.机器人操作的数学导论［M］.李泽湘，译.北京:机械工业出版社，1998.

［7］付奎生.两轴捷联稳定跟踪平台关键技术分析［J］.电光与控制，2009，16(7):53-55.

［8］Waldmann J. Line-of-sight rate estimation and linearizing control of an imaging seeker in a tactival missile guided by proportional navigation［J］. IEEE Transactions on Control System Tecnology，2002，10(4):556-567.

［9］董小萌，张平，王建立，等.三轴直角结构光电导引平台的捷联控制［J］.光电工程，2007，34(11):5-9.

［10］毛峡，张俊伟.办捷联导引头光轴稳定的研究［J］.红外与激光工程，2007，36(1):9-12.

［11］郑志伟.空空导弹系统概论［M］. 北京:兵器工业出版社，1997.