ANSYS在压力容器及管道缺陷评定中的应用

吴龙平 王文娜 明斐卿 姜 珊 张志强 赵 月

(1.中国石油天然气管道工程有限公司 2.河北石油职业技术学院)

ANSYS在压力容器及管道缺陷评定中的应用

吴龙平*1王文娜2明斐卿2姜 珊1张志强1赵 月1

(1.中国石油天然气管道工程有限公司 2.河北石油职业技术学院)

首先介绍了压力容器及管道缺陷评定的常用方法，即应力强度因子法和J积分法；然后阐述了ANSYS在压力容器及管道缺陷评定时的一般步骤；最后针对二维裂纹和三维裂纹进行了应力强度因子和 J积分计算，并与手工计算值进行了对比。结果表明，应用ANSYS对压力容器及管道进行缺陷评定是安全可靠的。

压力容器 管道 应力强度因子 J积分 断裂模型 裂纹尖端

断裂力学的思想是Griffith于1920年奠定的。他首先将强度与裂纹尺寸定量地联系在一起，对玻璃平板进行了大量的试验研究，提出了能量理论，建立了脆断理论的基本框架。然而，裂纹在外界因素作用下处于平衡或扩展，都与裂纹尖端的应力场有直接关系。为此，Irwin[1]在他人对裂纹尖端的应力和位移场进行分析而得到一组具有奇异性应力场的参量基础上，提出了一个新的力学参量——应力强度因子，并建立了相应的断裂判据。经过一段时间，Wells[2]于1963年提出了COD概念，其定义是裂纹体承载后，裂纹尖端沿垂直裂纹方向所产生的张开位移。虽然COD理论及其判据在中、低强度钢制压力容器及管道分析中得到了广泛应用，但COD值本身并不是一个直接而严密的裂纹尖端弹塑性应力应变场的表征参量，其理论分析和实验测定也都比较困难。于是，Rice[3]于1968年提出了J积分的概念。J积分是一个定义明确、理论严密的应力应变场参量，它不仅适用于线弹性的断裂分析，也适用于弹塑性的断裂分析，且又易于实验测定。此外，J积分还具有与积分路径无关的特点，故可避开对裂纹尖端处极其复杂的应力应变场的分析。

1 应力强度因子[4]

应力强度因子是描述裂纹尖端应力场强弱的断裂参量。在裂纹尖端，应力场具有奇异性。应力强度因子作为描述这种具有奇异性应力场的参量，当考虑裂纹尖端区域任意一点的坐标趋于奇异点时，穿透裂纹的应力强度因子的一般定义式为式 (1)。从式 (1)可以看出，要求解裂纹尖端的应力强度因子，只要把裂纹尖端的应力场先求出来，然后取其在裂纹尖端处的极值即可。

式中 r——裂纹尖端半径，mm；

σy——裂纹y方向的拉压应力，MPa；

τxy——裂纹x或y方向的剪切应力，MPa；

θ——裂纹与x轴的夹角， （°）。

裂纹尖端应力场的求解方法一般可分为四种：一是根据弹性理论按严格的边界条件求得相对精确的解析解，这种方法只适用于一些简单的断裂问题，如具有穿透裂纹的无限大平板等；二是根据弹性理论按近似的边界条件求得近似的解析解，这种解法实用于一些形状规则的裂纹体断裂问题，如三点弯曲试样和紧凑拉伸试样等；三是数值解法，如有限元法，这种解法实用于各种裂纹体的断裂问题，但只针对具体尺寸的裂纹体，无解析解；四是实验法，借助于实验手段来获得裂纹尖端区域的应力场分布。

对非穿透裂纹体来说，主要有椭圆片状埋藏裂纹和半椭圆状表面裂纹。其中，椭圆埋藏裂纹的应力强度因子表达式如式 (2）所示。

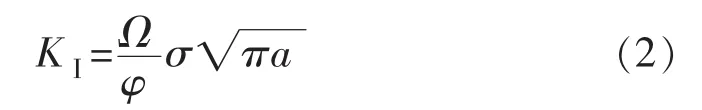
式中 Ω——考虑自由表面的影响而引入的修正系数，称为近表面修正系数。

式 （2）中的Ω与裂纹尺寸及裂纹在裂纹体中的位置有关，可按经验公式式 (3)、式 (4)、式 (5)计算。

式中 p1——埋藏裂纹至自由表面的最小距离，mm；

a——埋藏裂纹长半轴长度，mm；

c——埋藏裂纹短半轴长度，mm。

对表面裂纹来说，由于问题很复杂，用数学方法处理难度较大，其应力强度因子只能通过不同方法得到各种近似的计算公式来进行计算。式 （6）即为应力强度因子的一种近似计算式。

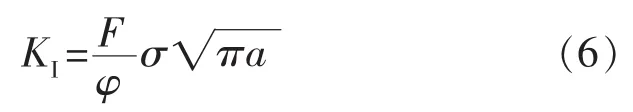
式中 F——前后表面修正系数，与裂纹尺寸和裂纹体的厚度有关。

目前关于F的表达形式很多，但是结果差别较大。我国在大量实验基础上，对近二十年来的20多个经验公式进行了综合评价， 认为其中Schmitt—Keim于1979年通过对受压圆筒裂纹能量释放率的有限元计算提出的公式，误差最小且又简单，其表达式如式 (7)所示。

2 J积分理论

J积分是Rice于1968年提出的。J积分是一个定义明确、理论严密的应力应变场参量，它不仅适用于线弹性的断裂分析，也适用于弹塑性的断裂分析，且又易于实验测定。此外，J积分还具有与积分路径无关的特点，故可避开对裂纹尖端处极其复杂的应力应变场的分析。

2.1 J积分的围线积分定义

在固体力学研究中，常利用一些具有守恒性质的线积分来分析裂纹周围的应力、应变场强度。所谓守恒性，指的是积分结果与积分路径没有关系。在分析二维裂纹体裂尖区域的应力、应变场时，J积分就是这种具有守恒性质的线积分之一。虽然J积分的定义式是由Eshelby推出的，但Rice首先认识到它在断裂力学上的应用。如图1所示，一穿透裂纹板，裂纹表面无载荷作用，但外力使裂纹产生了应力、应变场，则J积分的围线积分定义为

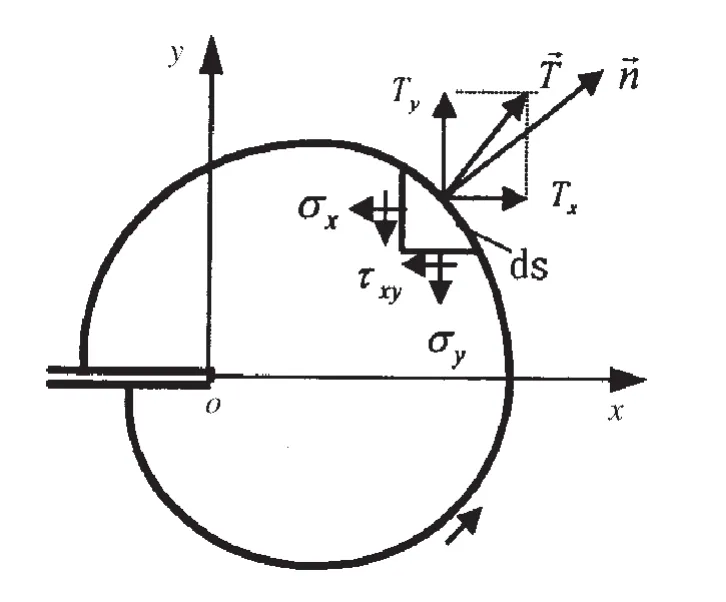
图1 J积分的积分路径

式中 Γ——自裂纹下表面任意一点按逆时针方向围绕裂纹尖端到裂纹上表面任一点的积分路径；

ds——回路Γ上的弧元素；

Tx、Ty——弧元素ds上的应力分量；

u、v——弧元素ds上的位移分量；

W——应变能密度。

2.2 能量定义式

根据J积分的围线积分定义式可以证明：在弹性阶段，J积分就是应变能释放率G。所以至少在弹性阶段，J积分具有明确的物理意义，即J积分是裂纹扩展单位面积时含裂纹体所释放的能量。

对于弹塑性阶段，可近似用形状和约束条件相同、分别具有相近裂纹长度a和a+Δa的两个二维含裂纹构件，在相同外载下产生的单位厚度总势能

的差异，作为弹塑性J积分的能量定义式。所以在从弹性到全面屈服整个变形阶段，J积分的能量定义式可表示为

式中 B——试件厚度，mm；

Π——总势能，Π=U-W，J；

U——应变能，J；

W——外力功，J。

J积分的能量定义式揭示了J积分的物理意义，将J积分值与宏观可测参量联系起来，对J积分的实验测试和解析分析都有重要意义。

3 应力强度因子和J积分的计算步骤

应力强度因子和J积分计算都是借助于软件ANSYS 14.0。下面具体介绍在软件ANSYS 14.0中的应力强度因子和J积分的计算方法。

为了计算应力强度因子和J积分，首先要建立断裂模型。其模型分为两种：2-D和3-D断裂模型。

3.1 2-D断裂模型

这里以三角形6节点实体单元PLANE 42为例作一介绍。在裂纹尖端的第一排单元应该是奇异的，如图2所示。在断裂模型中，KSCON是特别有用的，其作用是指定一个关键点处的单元划分尺寸，它能在特定关键点处自动产生奇异单元；同时它还控制周向的第一排单元的半径和数量。图3是借助于KSCON命令产生的断裂模型。其它的断裂模型应遵循以下原则：

图2 2-D奇异单元

图3 2-D有限元模型

(1)充分考虑对称性，在一些情况下，对称和反对称的断裂模型只需建立模型裂纹区域的一半，如图4所示。

(2)考虑到结果的合理性，在裂纹尖端周围的第一排单元半径应该为裂纹长度的1/8；在周向，每隔30°划分一个单元。

图4 对称模型和反对称模型

(3)裂纹尖端单元不应该扭曲。

3.2 3-D断裂模型

这里以六面体20节点单元SOLID 95为例作一介绍。在裂纹前沿的第一排单元应该为奇异单元，如图5所示。在创建3-D断裂模型中，创建2-D模型的KSCON命令不再使用，而是遵循以下原则：

图5 3-D奇异单元

(1)2-D断裂模型中的单元尺寸同样适用于3-D断裂模型。

(2)就曲线裂纹前沿而言，裂纹前沿的单元尺寸主要取决于局部曲线的数量；一般来说，沿裂纹前沿每隔15°到30°创建一个单元。

3.3 断裂参量的计算方法

首先进行静态分析，然后使用POST 1计算断裂参数。

3.3.1 应力强度因子

进行应力强度因子计算可按以下几个步骤进行。

（1）定义局部裂纹尖端或裂纹前沿坐标系，X轴平行于裂纹面 (在3-D模型中，X轴垂直于裂纹前沿)，同时Y轴垂直于裂纹面，如图6所示。具体命令如下：

Utility menu＞ WorkPlane＞ Local Coordinate Systems＞Create Local CS＞At Specified Loc

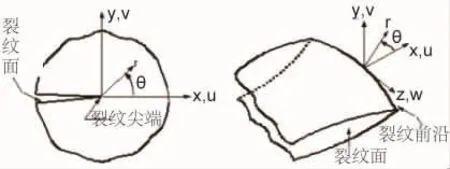
图6 裂纹尖端或裂纹前沿坐标

（2）沿裂纹面定义路径，第一个路径节点是裂纹尖端点。对半裂纹模型而言，需要两个沿着裂纹面的节点；对包括两个裂纹面的全模型而言，需要四个沿着裂纹面的节点，其中两个节点沿着一个裂纹面，另两个节点沿着另一个裂纹面，如图7所示。具体命令如下：

图7 半裂纹模型和全裂纹模型

Main Menu＞General Postproc＞Path Operations＞Define Path

（3）计算应力强度因子KⅠ、KⅡ、KⅢ。具体命令如下：

Main Menu＞General Postproc＞Nodal Cals＞Stress Int Factr

3.3.2 J积分

J积分是一种测量裂纹尖端附近的奇异应力和奇异应变而与路径无关的线积分。进行J积分计算可按以下几个步骤进行。

(1)读所需结果。具体命令如下：

GUI：Main Menu＞General Postproc＞Read Results＞First Set

(2)保存每个单元的体积和应变能。具体命令如下：

Main Menu＞General Postproc＞Element Table＞Define Table

(3)计算每个单元的应变能密度。具体命令如下：

Main Menu＞General Postproc＞Element Table＞Exponentiate

(4)定义线积分路径，见图8。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Define Path

图8 J积分计算路径

(5)将上述第 (3)项计算出的应变能密度映射到积分路径上。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Map onto Path

(6)对y进行积分。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Integrate

(7)将积分值赋给一个参数J。具体命令如下：

Utility Menu＞Parameters＞Get Scalar Data

(8)将应力分量SX、SY和SXY映射到路径上。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Map onto Path

(9)定义路径单位法向矢量。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Unit Vector

(10)计算式 (8)中的Tx、Ty。具体命令如下：

Main Menu＞General Postproc＞Path Operations＞Operation

(11)为便于计算位移矢量的导数，将积分路径向X正向或负向平移一小段距离。具体分为四个部分：

①计算路径平移的距离，如DX。一般而言，DX取路径总长度的1%；而路径总长度可以通过该命令获得。该命令为*Get,Name,Path,Last,S

②将积分路径沿X负方向平移DX/2的距离，并将位移UX和UY映射到路径上，如UX1、UY1。

③将积分路径沿X正向平移DX的距离，并将位移UX和UY映射到路径上，如UX2、UY2。

④将积分路径平移到原始位置，并借助于命令PCALC计算出 (UX2-UX1)/DX和 (UY2-UY1) /DY。

(12)借助于上述第(10)项和第(11)项对式(8)的第二部分的路径S进行积分，计算出第二部分的值。

(13)根据式 (8)，同时借助于第 (5)项至第(7)项和第 (12)项计算出J积分值。

4 应力强度因子和J积分的计算

4.1 二维中心裂纹板

问题描述：有一具有中心裂纹的长板，如图9所示。其中，裂纹板宽 2b=250 mm，高度 2h=1 mm，裂纹宽度2a=50 mm，板厚t=6.25 mm，E= 68 950 MPa，ν=0.3，σ0=0.003 9 MPa。因为符合平面应变情况，可认为是二维平板。

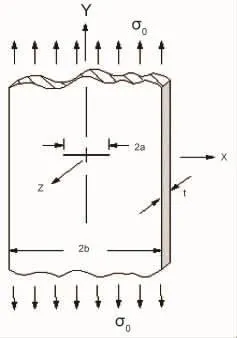
图9 二维中心裂纹板

经手工计算，可求得二维应力强度因子和J积分值分别为0.036 1 MPa·mm0.5和0.549 MPa·mm。而借助软件ANSYS求得的应力强度因子和二维J积分的值分别为 0.036 5 MPa·mm0.5和 0.583×10-7MPa·mm。

(1)设定σ0=6.895 MPa，保持其它条件不变，只改变裂纹尺寸，可以得到图10、图11所示的变化曲线。

(2)设定裂纹尺寸2a=250 mm，保持其它条件不变，只改变应力值，可以得到图12、图13所示的变化曲线。

从图10、图11可以看出，对于中心穿透裂纹来说，二维应力强度因子值和J积分值都与裂纹尺寸成抛物线关系，与实际规律基本吻合。

图10 应力强度因子随裂纹尺寸的变化曲线

图11 J积分随裂纹尺寸的变化曲线

从图12、图13可以看出，二维应力强度因子值与应力值成正比，而J积分值与应力值成抛物线关系，与实际规律基本吻合。

图12 应力强度因子随应力的变化曲线

4.2 三维圆裂纹柱体

问题描述：有一具有中心圆裂纹的圆柱体及其网格，如图14所示。其中，圆柱体半径，高度2h= 250 mm，E=68 950 MPa·mm，ν=0.3，σ0=8.274 MPa，r=10 mm，σ0不变，见图 15，r不变，见图16。从图15可以看出，三维应力强度因子值与裂纹尺寸大小关于x轴成抛物线关系，与实际规律基本吻合。从图16可以看出，三维应力强度因子值与应力值成正比例关系，与实际规律基本吻合。

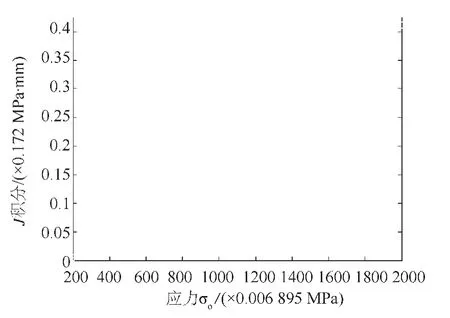
图13 J积分随应力的变化曲线

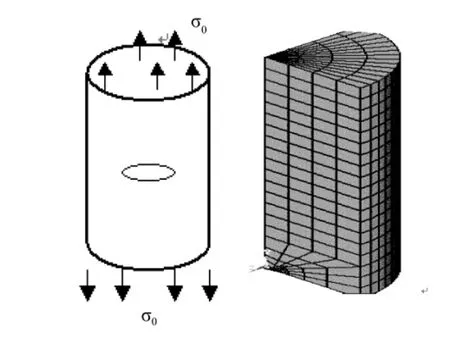
图14 含中心圆裂纹的圆柱体及1/4柱体有限元网格

图15 应力强度因子随裂纹尺寸的变化曲线

5 结论

通过二维中心裂纹板、三维圆裂纹柱体等应力强度因子与J积分的计算表明，本文推荐的应力强度因子和J积分的计算步骤与实际的二维应力强度因子值、三维应力强度因子值及二维J积分值是一致的。因此，本文推荐的应力强度因子和J积分计算方法是合理的。基于此，通过本文确定的应力强度因子与J积分可以作为压力容器及管道缺陷的评定方法之一。

图16 应力强度因子随应力的变化曲线

[1]Irwin G R.Analysis of stresses and strains near the end of a crack transversing a plate [J].Journal of Applied Mechanics，1957，24：361-364.

[2]Wells A A.Application of fracture mechanics at the beyond general yielding[J].British Welding Journal，1963，10：563-570.

[3]Rice J R.A path independent integral and the approximate analysis of strain concentration by notches and cracks[J]. J Appl Mech,1968,35：379-386.

[4]李国成.压力容器缺陷评定技术基础 [M].东营：中国石油大学出版社，1994.

The Application of ANSYS in Defect Assessment of Pressure Vessels and Pipelines

Wu Longping Wang Wenna Ming Feiqing Jiang Shan Zhang Zhiqiang Zhao Yue

Firstly,introduced the common methods for defect assessment of pressure vessels and pipelines, including stress intensity factor method and J-integral method.Secondly,illustrated the general steps of defect assessment for pressure vessels and pipelines by using ANSYS software.Finally,calculated the stress intensity factor and J-integral of two-dimensional and three-dimensional cracks,and compared the values with that from manual calculation.The results showed that the defect assessment of pressure vessels and pipelines with ANSYS software was safe and reliable.

Pressure vessel;Pipeline;Stress intensity factor;J-integral;Fracture model;Crack tip

TQ 050.1

2013-12-04）

*吴龙平，男，1979年生，工学硕士，高级工程师。廊坊市，065000。