倾斜微结构疏水表面液滴的滞后特性

蔡泰民，贾志海，贺吉昌，雷威

（上海理工大学能源与动力工程学院，上海 200093）

倾斜微结构疏水表面液滴的滞后特性

蔡泰民，贾志海，贺吉昌，雷威

（上海理工大学能源与动力工程学院，上海 200093）

倾斜微结构疏水表面液滴的滞后特性包括接触角滞后和滚动角。目前，具有较高精度的微结构疏水表面滚动角模型是以理想液滴形状为计算基础，忽略了重力、接触角滞后以及能垒引起的变形。本文以聚二甲基硅氧烷（PDMS）为基底，制备了方柱状微结构疏水表面，考虑疏水表面微观结构以及液滴大小两方面的因素，研究了倾斜微结构疏水表面液滴的滞后特性。从力和能量的角度对其影响机理进行了分析，通过滚动角理论值与实际值的比较发现，微方柱间距较大时，接触角滞后和能垒对滚动角影响显著，证实了该分析的合理性，为研究更加精确的滚动角模型奠定了理论基础。

微尺度；接触角滞后；滚动角；模型；能垒；受力分析；实验验证

在自然界中，可以发现水滴能够轻易地从荷叶表面滚落并带走污物，这就是所谓的“荷叶效应（lotus effect）”[1]。研究发现，在荷叶表面存在微米级“乳突”，乳突上布满纳米级的绒毛结构[2]。受此启发，研究人员通过光刻蚀[3-4]、材料喷涂[5]、化学腐蚀[6]等手段在疏水材料表面制备了微米结构、纳米结构以及微纳米两级结构，从而获得了各式各样的超疏水表面。超疏水材料因其具有诸多特殊性能，如抗黏附、抑冰霜[7-8]、除湿、自清洁[4]等，使其在诸多领域都有广泛的应用前景。倾斜微结构疏水表面液滴的滞后特性包括接触角滞后和滚动角，它们是表征材料超疏水性能的关键性参数。通过研究这些参数，有利于超疏水表面的制备及其表面微结构的几何优化[3-6，9-14]。

早在19世纪初，Young[15]就利用气、固、液之间的表面张力导出了关于平滑表面液滴接触角的预测公式，即Young’s方程，见式（1）。

式中，γlv、γsv、γsl分别为液气、固气、固液表面张力；θY为材料的本征接触角，即平滑表面的平衡接触角。Wenzel[16]视液滴完全浸润微结构疏水表面，于1936年提出了关于液滴在水平微结构疏水表面的表观接触角预测公式，即Wenzel方程，见式（2）。

式中，r为微结构疏水表面的粗糙度，即固体表面的实际面积与投影面积之比；θ为水平微结构疏水表面的表观接触角。Cassie和Baxter[17]进一步拓展了Wenzel方程，提出可以将粗糙不均匀的固体表面设想为一个复合表面，得到Cassie-Baxter方程，见式（3）。

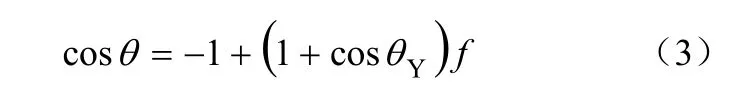
式中，f为固液接触的投影面积与整个表面的投影面积之比。由式（2）和式（3）可推导出更加完整的水平接触角预测公式[18]，见式（4）。

式中，rf为单个微柱的实际浸润面积与单个柱顶面积之比。当rf＞ 1时，该式用于预测混合浸润状态下的接触角；当rf= 1时，表示液滴的浸润深度为零，处于Cassie浸润状态，此时公式（4）转变为公式（3）。基本上，所有平滑表面液滴的运动模型都可以简化为式（5）[19]。

式中，k为待确定的系数；ρ、V、g分别为液滴密度、液滴体积及重力加速度；R为湿接触区域半径；α为平滑表面液滴的滑移角，或微结构疏水表面液滴的滚动角，统称临界倾斜角。

Frenkel[20]首次提出了一个精度相对较高的关系式，如式（6）。

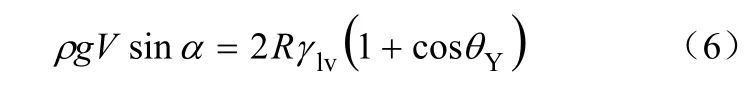
Olsen等[21]对式（5）进行了实验验证。Frenkel[20]还通过引入前进接触角和后退接触角，得到了另一个预测模型，见式（7）。

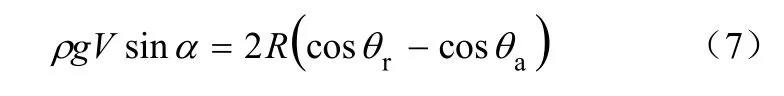
式中，θa和θr分别为倾斜表面上液滴的前进接触角和后退接触角。Furmidge[19]的实验结果和式（6）相吻合，但式（5）和式（6）都是液滴在平滑表面的滑移角数理模型。

目前，关于液滴在微结构疏水表面上的滚动角数理模型有两种。一种是Miwa等[22]在公式（4）的基础上提出的，仍然采用平滑表面的k值，但利用公式（3）修正了微结构疏水表面润湿区域半径R，从而得到微结构疏水表面的滚动角模型，见式（8）。

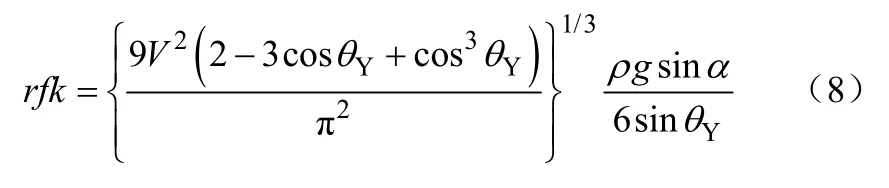
式中，k值由实验测得。由于k值的存在，公式（8）并不是纯理论模型，而是一个半经验公式。

另一种是由Lü等[23]从能量守恒及转化的角度提出，对相关变量近似地处理和取值，得到了一个精度相对较高的纯理论模型，见式（9）。

该模型以纯几何理想液滴形状为计算依据，而实际过程中，液滴不仅受重力的影响，还受接触角滞后和能垒的共同作用发生相应的变形。

观察发现，微结构疏水表面液滴主要存在两种典型的浸润状态，即Cassie状态和Wenzel状态，如图1(a)、图1(b)所示。另外还存在一种介于Cassie和Wenzel之间的混合状态，如图1(c)所示。液滴的浸润状态不同，导致其运动性质也存在巨大差异，Wenzel状态液滴由于侵入了表面微结构内，因此黏附性极强，相对于平滑表面，液滴更难从微结构疏水表面脱落；而Cassie状态液滴则悬停在微结构疏水表面，黏附性微弱，因此能够轻易滚落。混合状态则处在Cassie和Wenzel状态之间，其黏附性也介于两者之间，且具有不稳定性。由于混合状态的不稳定性以及Wenzel状态的极大滞后性，给研究微结构疏水表面液滴的接触角滞后特性带来极大的困难。为了简化问题的复杂性，本文采用Cassie-Baxter状态研究液滴在微结构疏水表面的滞后特性。

图1 微结构疏水表面水滴浸润状态

1 实验部分

1.1 微结构疏水表面结构及其制备

加工材料选用聚二甲基硅氧烷（PDMS），该材料的本征接触角θY为113.7°。图2为设计表面的方柱状微结构的扫描电子显微镜照片，其中a为方柱体边长，b为方柱间距，h为柱高。a、h分别为30μm、30μm，通过改变b得到不同的微结构疏水表面，其面积分数f分别为0.07、0.10、0.12、0.15、0.17、0.20、0.23，计算公式为f = a2/(a + b)2。采用微加工光刻的方法在其表面构筑微凸起柱状结构。首先，在硅片上旋涂厚度为30μm的SU8-25光刻胶；然后将掩膜板覆盖在US8-25上进行光刻，制作模子；最后将PDMS倒入模子中，在90℃的真空烘箱内放置约60min后取出，将PDMS聚合体从SU8膜上剥离，从而完成制备。

图2 方柱状微结构的扫描电子显微镜图像及基本几何参数

1.2 实验仪器与方法

实验仪器主要有上海Kino公司SL200B型接触角测量仪、荷兰FEI生产的QUANTA FEG 450场发射环境扫描电子显微镜（低真空状态下最小分辨率1nm）、日本奥林巴斯公司i-speed高速摄像仪（每秒25帧），液滴采用去离子水。

将PDMS微结构疏水表面固定在测量平台上，用水平仪对其进行水平调节，使其处于水平状态，采用躺滴法将去离子水按一定大小滴定在PDMS微结构疏水表面，保持液滴处于Cassie-Baxter状态，通过调节倾斜角（初始阶段，采用粗调，调节速度为1°/s；当接近预测滚动角时，采用细调，调节速度为0.1°～0.3°/s），待液滴刚开始滚动时，利用高速摄像仪记录液滴滚动过程，通过SL200B型接触角测量仪测量其前进接触角θa、后退接触角θr，同时记录临界倾斜角，即滚动角α。

2 结果与讨论

2.1 微结构间距的影响

为了研究微结构间距对滚动角的影响，将相同大小的液滴滴定在不同表面，测量得到前进接触角θa、后退接触角θr、接触角滞后CAH = θa-θr、滚动角α，并以面积分数f为横坐标，得到图3。分析发现，在液滴体积相同的情况下，随着面积分数f增大，接触角滞后CAH也增大。同时，可以看到接触角滞后CAH和滚动角α与面积分数f皆存在明显的制约关系，并且它们呈现相近的变化趋势。

进一步分析图3发现，相同大小的液滴在不同微结构表面上的前进接触角θa仅在一个很小的范围（165°～169°）内波动，发生较大变化的是后退接触角θr，随着f的增大（即间距的减小），θr从145°递减到124°，从而导致接触角滞后CAH逐渐增大。

研究认为，若忽略θa的微小波动对滚动角的影响，就可以通过研究后退接触线的受力分析来了解微结构是如何影响滚动角的。本文进行了液滴后退接触线的运动过程中的受力分析，以及相同大小的液滴在不同微结构尺寸的疏水表面后退接触线受力分析的比较，如图4所示。在图4(b)中，因为液滴在水平微柱上具有微小的浸入，所以此时三相接触线上的固液表面张力γsl的方向应是竖直向上的，并且与气液表面张力γlv的竖直分力、固气表面张力γsv以及单个微柱所承受的由液滴重力引起的单位三相接触线上所受的力fG达到平衡。

图3 不同大小的液滴各临界参数与微结构尺度的关系

随着倾斜角的增加，当到达临界倾斜角（即滚动角α）时，液滴的后退接触线将到达微柱顶面的后边缘，此时的受力将变得非常不稳定，γsv和γsl方向的变化并非一个渐变的过程，而是突变，其方向要么垂直于基底，要么平行于微柱顶面，如图4(c)、4(d)所示。若继续增大基底的倾斜角，或者在外界的干扰下，若γsv和γsl的方向倾向平行于运动方向，由于γsl-γsv=-γlvcosθr＞0 （θr＞90°），液滴的后退接触线将很快位移到微柱顶面内侧，如图4(e)，此时液滴后退接触线将迅速地滑过微柱顶面，并从微柱顶面的后边缘阶跃到下一个微柱顶面前边缘。

对于不同微结构尺寸的微结构疏水表面，相同大小的液滴在到达滚动角时，其后退接触角是不同的，如图4(f)所示，虚线表示在面积分数较大的微结构疏水表面的液滴气液界面，此时的后退接触角小于在面积分数较小的微结构疏水表面的液滴的后退接触角，显然，此时的气液表面张力在平行于液滴运动方向上的分力将减小。随着面积分数的减小，液滴后退接触线上的气液表面张力γlv的平行分力将增大。换句话说，随着微柱间距的增大，即面积分数的减小，液滴滚动的过程中所克服的黏附力减小了，但由气液表面张力产生的阻力却增大，从而导致滚动角实际值偏大于公式（9）的理论值。

另一方面，液滴在微结构疏水表面上的滚动不仅要克服黏附功WA（work of adhesion）[24]，还要克服相应的能量势垒EB（energy barrier）[25]。目前，关于能垒EB的具体表达式尚未获得，但分析可以知道它与液滴大小V、微结构尺寸f，甚至与滚动角α都有密不可分的联系。随着微柱间距b的增大，即面积分数f的减小，能垒EB也相应的增大。但具体是如何影响能垒的，本文提出了用于定性分析能垒大小的原理图，如图5所示。

图5(a)、5(b)中的液滴大小相同，由于表面结构尺寸不同，它们的后退接触角和滚动角都有所不同。很显然，图5(a)的微柱间距小于图5(b)的微柱间距，相应的滚动角图5(a)大于图5(b)。随着倾斜角的增大，液滴所需克服的能垒在减小。显然，当它们到达各自相应的滚动角时，液滴所克服的能垒才是实际克服的能垒，亦称临界能垒EBcritical。

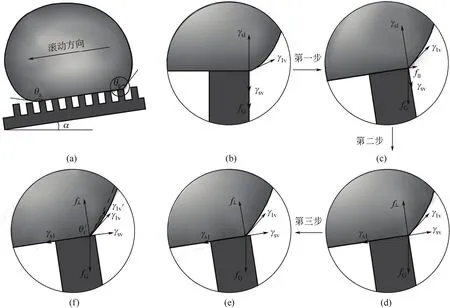
图4 微结构疏水表面液滴后退三相接触线上的受力分析

图5 相同大小的液滴在不同结构尺寸倾斜表面的临界滚动示意图

如图5所示，在靠近后退接触线的第二个微柱前端，垂直于水平面画一条虚线，将液滴分隔成两部分，用V1和V2表示。液滴在滚动的过程中，首先在微柱上的运动属于滑移行为，接着在凹槽上方发生阶跃行为。在凹槽上方液滴的后退部分V2失去了微柱对它的支撑力，取而代之的是液滴的前进部分V1对V2的“牵引力”，换句话说，此时V2对V1产生一定的阻力，V2越大，产生的阻力就越大，V1越小，产生的牵引力就越小。那么在凹槽上方的阶跃就需要克服相应的能垒。显而易见，随着微柱间距b增大，V2将增大，V1将减小，即V2/ V1增大。如图5(b)所示，为了以示区分，此时液滴的前进和后退部分分别用V1'、V2'表示，从图5中可以看出，此时V2'/ V1' ＞ V2/ V1，且V1+ V2= V1' + V2' ，那么图5(b)中液滴的临界能垒EBcritical将大于图5(a)，从而导致图5(b)中液滴的实际滚动角将更加偏离公式（9）的理论值。

2.2 液滴体积的影响

众多研究表明，液滴体积对滚动角的影响具有一定规律，如式（5）～式（9）。但关于液滴大小对接触角滞后的影响却研究甚少。本文对不同微结构间距的疏水表面，分别进行了不同大小液滴的接触角滞后现象的研究，如图6所示。

由图6可知，当面积分数f相同时，随着液滴体积V的变化，前进接触角θa和后退接触角θr皆在一个很小的范围内波动，并且波动具有一致性，即θa和θr同增或同减，导致其接触角滞后CAH基本不变。由此可知，接触角滞后CAH与液滴体积V并没有明显的制约关系。

2.3 滚动角理论值与实际值的比较

公式（9）是以理想的液滴形状为计算基础的，忽略了重力、接触角滞后以及能垒的共同作用所引起的变形。本文利用公式（9）的理论值与实验测量值进行比较。由于公式（9）是建立在微方柱结构表面上的数理模型，为了比较的可靠性，实际值也采用微方柱结构表面的实验数据，如图7所示。

由图7可知，当面积分数f为0.15、0.20、0.23时，其模型预测的准确度相对较高；当f 为0.07、0.10、0.12时，其误差较大，可以认为该模型在f为0.07、0.10、0.12的情况下已经失效。换句话说，滚动角实验值与理论值存在偏差，并且实验值大于理论值。当f较小时，其偏差较大；当f较大时，其偏差较小。由此可知，微结构间距b较大时，接触角滞后和能垒对滚动角影响越显著，从而证实了本文从力和能垒角度分析微结构对滚动角的影响的合理性。

图6 不同微结构尺度倾斜表面各临界参数与液滴体积的关系

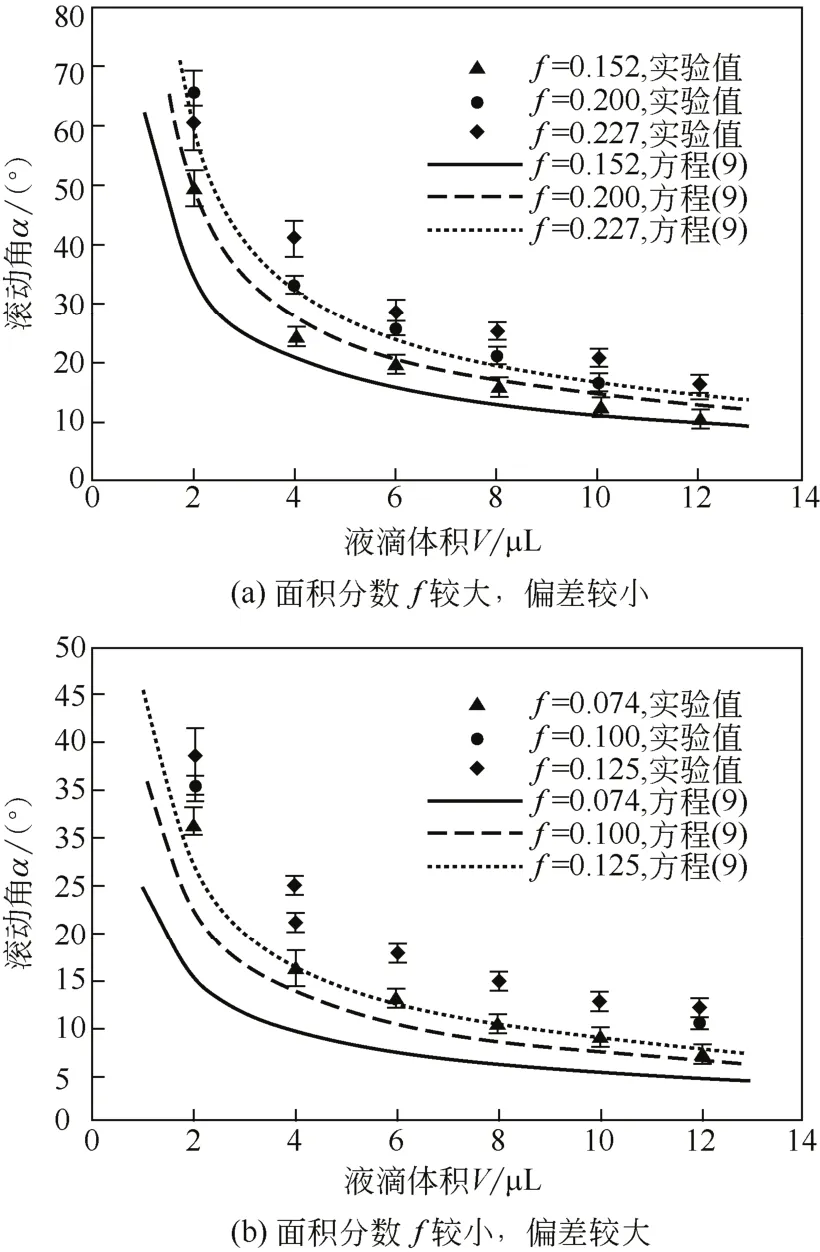
图7 实验测得值与模型预测值的比较

3 结 论

接触角滞后CAH与液滴体积V没有明显的制约关系，而是与表面微结构有着密不可分的联系。随着微结构间距b的增大，即面积分数f的减小，相同大小的液滴其前进接触角θa在一个很小的范围（165°～169°）内波动，后退接触角θr逐渐从124°增大到145°，导致接触角滞后CAH（=θa-θr）逐渐减小。

微结构间距b较大，即面积分数f较小时，接触角滞后CAH和能垒EB对滚动角α的影响不容忽视，并从力和能垒的角度分析了微结构间距对滚动角的影响机理。分析表明，由于接触角滞后和能垒的存在，实际滚动角与方程（9）的理论滚动角将存在偏差，并且实际滚动角大于方程（9）的理论滚动角，特别是在微结构间距b越大，即面积分数f较小时，其偏差将较大，这与实验现象完全吻合，从而证实了该分析的合理性，同时为研究更加精确的滚动角模型奠定了理论基础。

符 号 说 明

Α—— 平滑表面液滴的滑移角或微结构疏水表面液滴的滚动角，统称临界倾斜角，（°）

a，b，h—— 分别为微方柱体边长、柱间距、柱高，µm

CAH—— 接触角滞后，（°）

EB，EBcritical—— 分别为能量势垒和临界能垒，J

f—— 固液接触的投影面积与整个表面的投影面积之比

fG—— 单个微柱所承受的由液滴重力引起的单位三相接触线上所受的力，mN/m

g—— 重力加速度，N/kg

k—— 待定系数

L—— 单个微柱上的三相接触线长度，m

R—— 湿接触区域半径，m

r—— 粗糙度，即固体表面的实际面积与投影面积之比

rf—— 单个微柱的实际浸润面积与单个柱顶面积之比

V—— 液滴体积，µL

V1，V2—— 分别为液滴在倾斜微结构疏水表面的前进部分和后退部分，µL

WA—— 黏附功，J

γlv，γsv，γsl—— 分别为液气、固气、固液表面张力，mN/m

θ—— 水平微结构疏水表面的表观接触角，（°）

θa，θr—— 分别为倾斜表面上液滴的前进接触角、后退接触角，（°）

θY—— 杨氏接触角或称材料的本征接触角，即平滑表面的平衡接触角，（°）

ρ—— 液滴密度，kg/m3

[1] Barthlott W，Neinhuis C. Purity of the sacred lotus，or escape from contamination in biological surfaces[J].Planta，1997，202（1）：1-8.

[2] Feng Lin，Li Shuhong，Li Yingshun，et al. Super-hydrophobic surfaces：From natural to artificial[J].Adv.Mater.，2002，14（24）：1857-1860.

[3] Zhao Hong，Park Kyoo-Chul，Law Kock-Yee. Effect of surface texturing on superoleophobicity，contact angle hysteresis，and“robustness”[J].Langmuir，2012，28（42）：14925-14934.

[4] Zhao Hong，Law Kock-Yee. Effect of surface texturing on superoleophobicity[J].Langmuir，2012，28（32）：11812-11818.

[5] Li Hui，Zhao Yunhui，Yuan Xiaoyan. Facile preparation of superhydrophobic coating by spraying a fluorinated acrylic random copolymer micelle solution[J].Soft Matter.，2013，9：1005-1009.

[6] Trong Thi Mai，Chang Quan Lai，Zheng H，et al. Dynamics of wicking in silicon nanopillars fabricated with interference lithography and metal-assisted chemical etching[J].Langmuir，2012，28（32）：11812-11818.

[7] 丁云飞，殷帅，廖云丹，等. 纳微结构疏水表面结霜过程及抑霜特性[J]. 化工学报，2007，63（10）：3213-3219.

[8] 周艳艳，于志家. 铝基超疏水表面抗结霜特性研究[J]. 高校化学工程学报，2012，26（6）：929-933.

[9] Balu B，Berry A D，Patel K T，et al. Directional mobility and adhesion of water drops on patterned superhydrophobic surfaces[J].J.Adhes.Sci.Technol.，2011，25（6）：627-642.

[10] Rahman M A，Jacobi A M. Wetting behavior and drainage of water droplets on microgrooved brass surfaces[J].Langmuir，2012，28（37）：13441-13451.

[11] Park J，Lim H，Kim W，et al. Design and fabrication of a superhydrophobic glass surface with micro-network of nanopillars[J].Journal of Colloid and Interface Science，2011，360（1）：272-279.

[12] 贾志海，雷威，贺吉昌，等. 振动诱导微结构粗糙表面水滴Wenzel-Cassie状态转变特性[J]. 化工学报，2014，65（2）：544-549.

[13] Hensel R，Helbig R，Aland S，et al. Wetting resistance at its topographical limit：The benefit of mushroom and serif T structures[J].Langmuir，2013，29（4）：1100-1112.

[14] Hong Siang-Jie，Chang Cheng-Chung，Chou Tung-He，et al. A drop pinned by a designed patch on a tilted superhydrophobic surface：Mimicking desert beetle[J].J.Phys.Chem.C，2012，116（50）：26487-26495.

[15] Young T. An essay on the cohesion of fluids[J].Phil.Trans.R.Soc.Lond.，1805，95：65-87.

[16] Wenzel R N. Surface roughness and contact angle[J].J.Phys.Chem.，1949，53（9）：1466-1467.

[17] Cassie A B D，Baxter S. Wettability of porous surfaces[J].Trans. Faraday Soc.，1944，40：546-551.

[18] Marmur A. Wetting on hydrophobic microstructured hydrophobic surfaces：To be heterogeneous or not to be?[J].Langmuir，2003，19（20）：8343-8348.

[19] Furmidge C G L. Studies at phase interfaces. I. The sliding of liquid drops on solid surfaces and a theory for spray retention[J].J.Colloid Sci.，1962，17：309-324.

[20] Frenkel Y I. On the behavior of liquid drops on a solid surface：1. The sliding of drops on an inclined surface[J].Exp.Theoret.Phys. （US SR），1948，18：659.

[21] Olsen D A，Jouner P A，Olson M D. The sliding of liquid drops on solid surfaces[J].J.Phys.Chem.，1962，66（5）：883-886.

[22] Miwa M，Nakajima A，Fujishima A，et al. Effects of the surface roughness on sliding angles of water droplets on superhydrophobic surfaces[J].Langmuir，2000，16（13）：5754-5760.

[23] Lü Cunjing，Yang Changwei，Hao Pengfei，et al. Sliding of water droplets on microstructured hydrophobic surfaces[J].Langmuir，2010，26（11）：8704-8708.

[24] Li J G，Coudurier L，Eustathopoulos N. Work of adhesion and contact-angle isotherm of binary alloys on ionocovalent oxides[J].Journal of Materials Science，1989，24（3）：1109-1116.

[25] Morita M，Koga T，Otsuka H，et al. Macroscopic-wetting anisotropy on the line-patterned surface of fluoroalkylsilane monolayers[J].Langmuir，2005，21（3）：911-918.

Hysteresis characteristics of droplets on inclined microstructured hydrophobic surfaces

CAI Taimin，JIA Zhihai，HE Jichang，LEI Wei
（University of Shanghai for Science and Technology，Shanghai 200093，China）

Hysteresis characteristics of droplet on inclined microstructured hydrophobic surfaces include contact angle hysteresis （CAH） and sliding angle （SA）. The SA model of droplet on microstructured hydrophobic surfaces，which has a relatively higher precision，is based on ideal droplet shape for calculating，ignoring the distortion of droplet caused by the combined action of gravity，CAH and energy barrier （EB）. In this paper，micro-pillar-structured hydrophobic surface was prepared from polydimethylsiloxane （PDMS），and CAH and SA were studied in terms of micro-pillar spacing and droplet size. With the increase of micro-pillar spacing，advancing contact angle of droplet with the same size basically remained unchanged，but receding contact angle decreased. For droplets with different sizes，on the same substrate，advancing contact angle and receding contact angle slightly changed，but CAH basically remained unchanged. Force analysis was conducted on the receding three-phase contact line，and the effects of CAH and EB on SA were analyzed from the perspectives of force and energy. By comparing theoretical value and practical value of SA，the significance of their effects on SA was confirmed，verifying the rationality of the analysis with respect to the effects of micro-pillar spacing on SA from the perspectives of force and EB respectively，which contributed to studying the more precise SA model.

microscale；contact angle hysteresis；sliding angle；model；energy barrier；force analysis；experimental validation

TQ 051.5

A

1000-6613（2014）08-2123-07

10.3969/j.issn.1000-6613.2014.08.030

2014-02-26；修改稿日期：2014-03-24。

国家自然科学基金（51176123）、上海市自然科学基金（11ZR1424800）及高等学校博士学科点专项科研基金（20103120120006）项目。

蔡泰民（1989—），男，硕士研究生。联系人：贾志海，副教授，主要从事先进功能材料在动力工程领域的应用研究。E-mail zhhjia@usst.edu.cn。