资源配置可持续发展的动态博弈
2014-07-02段妍骥
段妍骥
(马里兰大学 商学院,美国 马里兰州 20740)
可持续发展是是人类生存的必要条件。当今社会中,可持续发展已经越来越为人们所广泛接受。从国际组织签订的各种公约到各国提出的发展战略,从法律层面的约束到人们观念的进步,可持续发展已经日益成为各国未来的趋势与目标。不管在当代或未来,可持续发展都要解决人类生存和资源消耗的矛盾,都必须通过对资源进行合理的配置才能达到二者的均衡。
博弈论是研究决策者在决策主体各方相互作用情况下如何进行决策及有关这种决策的均衡问题的理论。博弈论强调决策主体各方策略的相互依存性,即任何一个决策主体必须在考虑其他局中人可能的策略选择的基础上来确定自己的最优行动策略。本文拟运用博弈的方法对资源配置进行研究。
基本假设:1.假设市场上只有一个资源开发商和一个政府。2.假设政府会对资源的开采进行干预。
一 资源两种状况时的两期模型
资源两种状况指资源不稀缺和资源稀缺,两种状况的差异构成了不同的两期模型。
当资源不稀缺时,当代人们对该资源的需求可以得到完全满足,同时也不会影响后代对这种资源的使用。因此,在这种情况下,效率与公平是并存的。假设某种可耗竭资源的市场价格为2,其需求函数为p=8-0.4q,对于不考虑贴现率(指将未来资产折算成现值(present value)的利率)的静态的两期模型,求其均衡解只要使mc=mr,可得q1=15,q2=15。如果这种资源的总量大于 30,那么这种资源可以满足当代和未来人们的需求。无论如何分配,这种配置都是有效率并且公平的。因此在这个时候,政府是不需要对开发商进行干预的。图1:
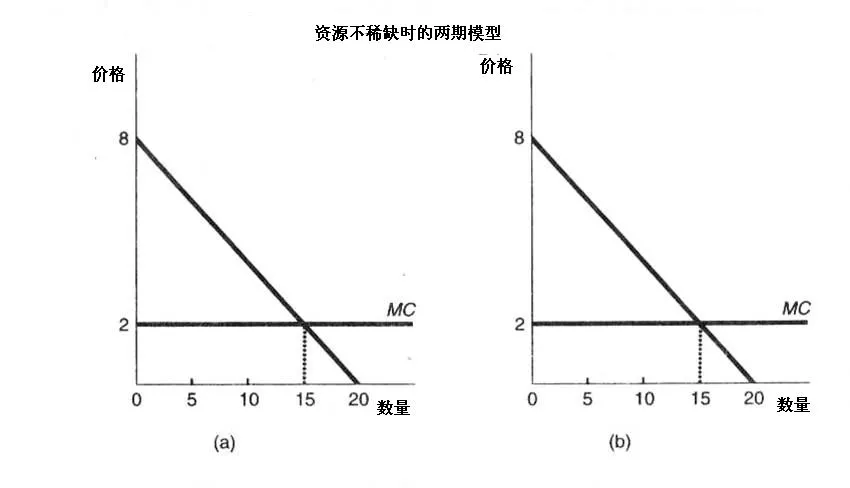
然而,这种情况是不可能的。首先,可耗竭资源随着时间的流逝都将减少,成为稀缺资源;其次,贴现率的存在会使资源配置缺乏均衡性。
因此我们应该从动态的角度,加入贴现率和时间因素分析资源稀缺时的两期模型。
由于资源的永远不稀缺只是一种理想的假设,因此我们应当假设资源的总量不足以满足当代人和未来人的需求。假设某种可耗竭资源的市场价格为2,其需求函数为p=8-0.4q,同时资源总量为20,贴现率为0.1,为了求得均衡解,必须使将来的边际净收益(指增加一单位产品的销售所增加的收益,即最后一单位产品的售出所取得的收益。)的现值与当前的边际净收益相等。即需要使等式
(1).q1+q2=20
(2).8-0.4q1-2=(8-0.4q2-2)/1+0.1
成立,通过解答方程,可以得到 q1=10.238,q2=9.762。这种资源配置可以使得边际净收益的现值最大,从而是一种有效率的配置方式。这种资源配置的方式适用于多种配置政策,包括市场配置,政府配给或者限额政策等,都可以从这种配置方法中得到均衡。图2:
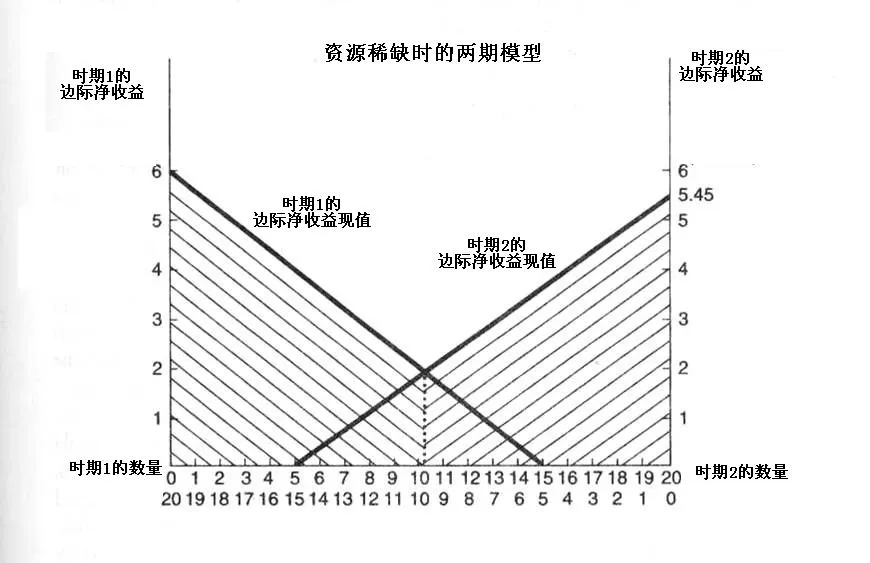
由于在长时间里,资源是稀缺的,这将会导致边际使用者成本的出现。边际使用者成本是指那些我们目前没有将某种资源的稀缺纳入考虑而过度使用它们,从而使我们的后代遭受到额外损失的那些损失的现值。
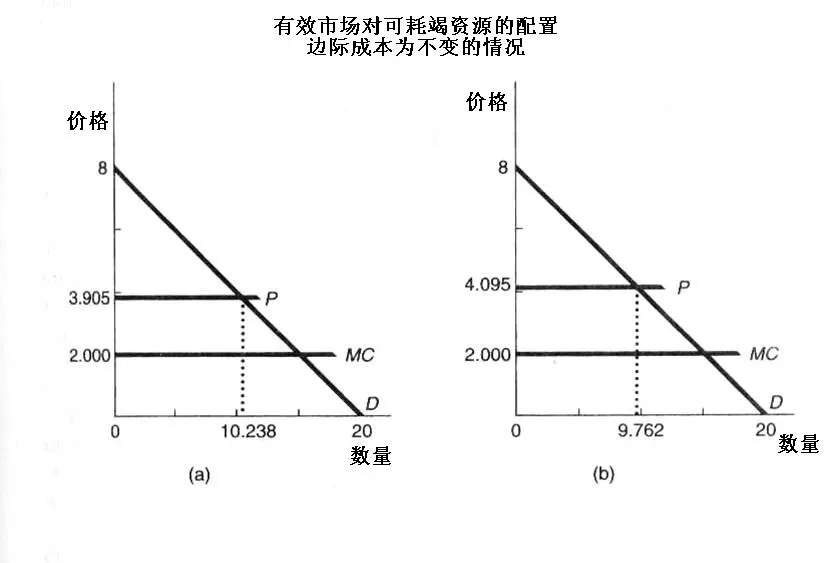
显然,当资源不稀缺时,当代和未来的人们都可以获得满足自身需要的资源,因此,稀缺性不存在时,边际使用者成本也不存在,这时,该资源的价格应该等于它的边际成本。
但是,一旦资源稀缺时,即边际使用者成本存在时,这种资源的价格就会增加,即价格等于它的边际成本与边际使用者成本的和。通过图2可以反映出资源稀缺时价格的变化。已知两期的资源分配为q1=10.238,q2=9.762,将它们带入逆需求函数p=8-0.4q,可以求得p1=3.905,p2=4.095,在第一期,由于资源稀缺带来的边际使用者成本是3.905-2=1.905,第二期的(实际的)边际使用者成本是4.095-2=2.095,将第二期的(实际的)边际使用者成本换成现值2.095/(1+0.1)可得它也是1.905,因此两期的边际使用者成本是相等的,但是这说明实际的边际使用者成本是增加的。这种增加是由于贴现率的存在,使得当前与未来的资源配置不相等,且贴现率介于0到1之间,现值pv=Bn/(1+r)^n。由此可知,贴现率r越大,该资源在未来使用的现值会越小,该资源在未来的配置也会越少。图3:
二 政府在资源配置中的动态博弈
之前两期模型所提到的有效的资源配置尽管能做到使边际净受益现值的最大化,但是它在一定程度上是不公平的。因为贴现率的存在必然导致该资源在未来的分配较现在的分配少,这与可持续发展的观念相悖,会使资源过快消耗而给我们后代的生存带来困难。因此我们需要从可持续的角度探寻一个更为公平的资源配置方式。
为了追求一个更为公平的资源配置,我们假设政府会对资源的开采者进行干预,设定一个开采的限额,对超出限额的部分采取罚款的方式。这样就能将部分的开采资源带来的外部性内部化,从而使开采者承担一定的边际使用者成本。尽管这样,当开采者过度开采某种资源所获利益大于罚款损失时,某些开采者仍然会选择过度开采,从而导致资源的过度消耗。因此,应当建立一个有效的遏制机制,将政府的罚款行为变成一个“可置信威胁”。
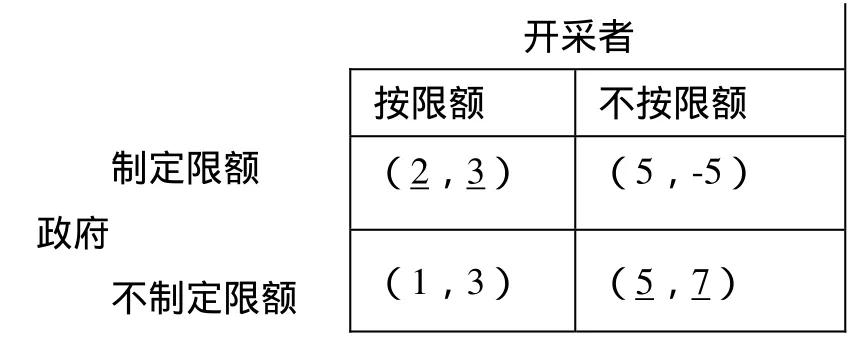
开采者制定限额政府不制定限额按限额 不按限额(2,3) (5,-5)(1,3) (5,7)
首先,这个博弈属于完全信息静态博弈,政府有制定限额和不制定限额两种策略,开采者有按限额开采和不按限额开采两种选择。
通过矩阵的形式来表达这个博弈,现分析如下:
(1)如果政府制定限额,开采者按限额开采,那么政府能成功地维持一个公平的资源共享的环境,同时也能获得较好的声誉,但是开采者获得的利润较少;政府的收益为2,开采者的收益为3。
(2)如果政府制定限额,但是开采者却不按限额完成而过度开采,这样会导致政府对开采者进行罚款,从而使政府获得罚金,收益为5,开采者信誉受损并且还要被罚款,收益为-5。
(3)如果政府不制定限额,但开采者却遵循一个公平的开采量,政府的收益较小为1,开采者的收益为3。
(4)如果政府不制定限额而开采者也过度开采,政府能从开采者那里获得更多的税收收益,政府的收益为5,而开采者由于过度开采能获得7的收益。
通过这个矩阵,我们发现没有严格占优策略均衡,只存在两个混合策略均衡,即(制定限额,按限额开采)和(不制定限额,不按限额开采)。就是说,双方的决策都要根据对方的选择来决定。
虽然,(制定限额,按限额开采)是该矩阵的一个均衡解,但是这个均衡解达成的条件是开采者认为政府的罚款比过度开采所获得的利润大,这就要求政府制定一个合理的处罚标准,下面通过机制设计来研究政府应如何制定过度开采的罚款标准。
由于政府事先不知道开采者对收益预期的相关信息,因此该博弈转化成一个不完全信息静态博弈。假设政府制定一个限额,限额为10(而不是之前求得的具有效率的10.238),开采者如果没有超出限额,其开采成本为x1,但如果对超出限额的部分要增加罚款,那么开采者的成本上升为x2,这种资源的价格为2,设实际开采数量为q,则:
E(不超过限额)=2*10-x1*10=20-10x1
E(超过限额)=2*q-(x1*10+x2(q-10))=2q-10x1-qx2+10x2
制定罚款的目的是使不超过限额的预期收益大于超过限额的预期收益,即:
2q-10x1-qx2+10x2>20-10x1
化简得(-q+10)x2<-2q+20 因为q一定大于10,
所以可得x2>2
即政府制定的罚款的价格应该大于该资源的市场价格,这样就能使开采者限制自己的开采量,去承担一部分使用者成本,使可持续发展成为可能。因此,我们认为:为了真正做到可持续发展所要求的,既满足当代人的利益,也不损害后代人的利益,政府应该采取一些措施敦促和监督企业,减少对可耗竭资源的开采量。而企业也不能只注重眼前的经济利益,应该从可持续发展的角度来决定资源开采量,而不能为了追求经济利益而过度开采。
[1]Sustainability,water resources and regulation[A].C.Cocklin,G.Blunden, Ecological Economics[C].Volume 29,Issue 1,February 1998:51-68.
[2]Sustainability of an economy with an exhaustible resource:A viable control Approach[A].V Martineta,L.Doyenb,Resource and Energy Economics[C].Volume29,Issue 1,January 2007:17-39.
