基于MATLAB 的工业机器人码垛单元轨迹规划

王鲁平，朱华炳，秦 磊

(合肥工业大学 机械与汽车工程学院，合肥 230009)

0 引言

码垛机器人代替人工可以进行高强度高精度重复性的物料搬运工作，具有广阔的应用与发展前景［1］。在对码垛机器人的研究中，轨迹规划问题是一个重要的研究方向。目前实际生产中工业机器人编程主要使用在线示教再现编程。这一编程方法操作直观简便，操作者可根据现场实际情况灵活进行编程，但面对小批量、复杂多变的生产情况，这一编程方式效率较低，并受操作者素质、经验等复杂因素影响，易于出现错误［2］。通过离线仿真实验，可以根据不同实际生产情况建立机器人工作单元模型，在综合考虑机器人重复定位精度等复杂因素的条件下，对末端执行器路径进行设计，进而对机器人进行轨迹规划，模拟机器人动态特性，直观地显示机器人运动情况，对生产过程中的机器人单元编程起到指导作用。本文以合肥工业大学工程认知博物馆FANUC M-10iA 机器人码垛工作单元实物为例，通过实验获得实际工况下机器人重复定位精度参考值，基于MATLAB Robotics 对机器人工作单元进行了运动学仿真，对机器人码垛过程进行了轨迹规划。

1 FANAC M-10iA 机器人运动学模型

1.1 FANAC M-10iA 机器人运动学正解模型

FANUC M-10iA 机器人是一种精密多关节工业机器人，具有六个转动关节，即六个自由度。各转动关节由交流伺服电机驱动，可以满足驱动大惯性力矩负载和快速运动精确定位的要求。机器人本体由基座，机身，臂部，手腕及手部组成。其中基座主要起支撑作用，链接机身与基座的J1 关节产生回转运动，大臂与机身构成的J2 关节驱动大臂的仰俯运动，大臂与小臂构成的J3 关节驱动小臂的仰俯运动，J4，J5，J6 关节驱动手臂的横摆，手腕的仰俯及旋转运动(图1)。机器人手臂末端可安装不同的末端执行器，以满足不同工况的需求［3］。

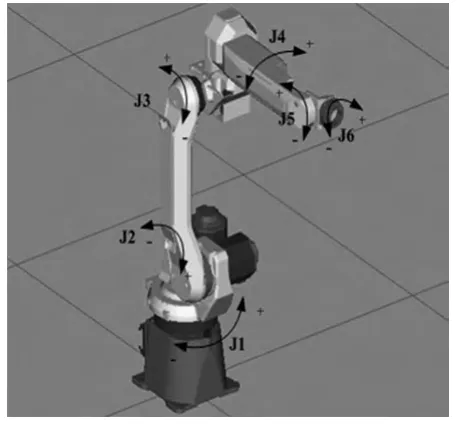
图1 FUNAC M-10iA 机器人三维结构

根据D-H 参数法［4-5］，确定了FANUC M-10iA 机器人各关节坐标系，将连杆坐标系按坐标系编号依次变换，建立4 ×4 变换矩阵表征其与前一杆件坐标系的变换关系。x0y0z0为固定参考坐标系，称为基座坐标系，xiyizi与机器人第i个杆件固连，坐标原点在第i+1 个关节的中心点处。杆件长度ai-1为沿xi轴从zi-1到zi的距离;扭转角αi-1为绕xi-1从zi-1到zi旋转的角度;偏移距di为沿zi从xi-1到xi的距离;关节角θi为绕zi从xi-1到xi旋转的角度;建立的连杆坐标系见图2，连杆参数与关节变量的D-H 参数表见表1。

图2 M-10iA 机器人D-H 连杆坐标系

表1 FANUC M10-iA 机器人D-H 参数表

由D-H 参数和齐次变换公式可求得两杆之间的位姿矩阵Ti:

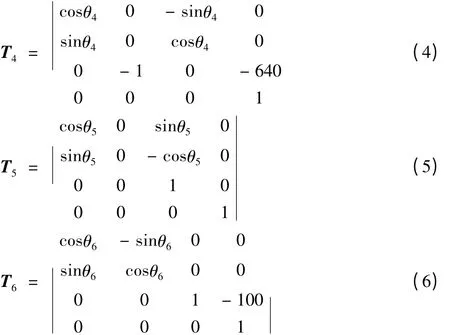
由上式得出机器人从基座到末端执行器的总齐次变换公式:

式中:nx、ny、nz为末端执行器法向矢量;ox、oy、oz为方向矢量;ax、ay、az为接近矢量;px、py、pz为位置坐标。

由式(7)可得出末端执行器位置坐标与各关节转角关系:

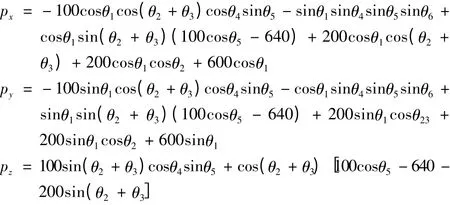
1.2 机器人逆运动学分析

在轨迹规划过程中，需要在已知末端执行器到达点位姿的情况下求解对应关节变量值，即求运动学逆解。运动学逆解需要考虑机器人可达空间的制约，并存在多解的问题。对于本文研究的码垛任务，预先在笛卡尔空间内对轨迹途径的关键点进行选定，将较复杂的运动路径分解成在关键点间的分段运动，进而采用代数法求逆解，将逆解问题简化［6］。

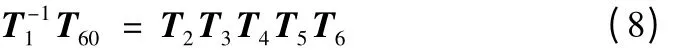
将(8)式两边展开，根据等式两边矩阵含θ1部分对应相等，解出θ1。同理，可依次解出其它各关节角θ2-6。

2 FANUC M-10iA 机器人工作单元建模

本文讨论的机器人工作单元包括机器人本体，物料托架以及16 个250mm ×250mm ×250mm 的物块。机器人水平安装于料台前的地面，料台上摆放着16 个正方体物块。机器人码垛工作即为将这些摆放在料台一侧的正方体物块依次搬运到料台的另一侧。为了实现搬运工作，机器人腕部附加了吸盘作为末端执行器，见图3。

图3 FANUC M-10iA 码垛单元实物

根据前述D-H 参数，在Matlab 环境下使用Robotics 工具箱Link 函数L= link(［alpha A theta D sigma］)对机器人本体完成建模［7］。完成的机器人本体运动学模型见图4。

图4 Funac M-10iA 机器人运动学模型

在Matlab 软件中有多种方式进行三维形体的建模，本文采用了voxel 函数，可以对三维空间中特定位置的长方体物块进行绘图［8］。voxel 函数可以对对象的位置、尺寸及透明度进行定义，多个voxel 绘制出的图形可以叠加在一起形成形状较为复杂的对象，能较好地模拟工作空间内机床、物块、料台等对象的几何特征与空间位置，可以满足多变的工作空间的建模需求。在Matlab 环境下对工作单元的建模简便快捷，可以很好地适应多变的实际工况，能直观地为机器人轨迹规划提供参照［9］。本文以M-10iA 机器人码垛任务单元为例，其初始状态见图5。

图5 M-10iA 机器人工作单元初始状态图

3 工业机器人末端执行器的轨迹规划

3.1 重复定位精度测量实验

工业机器人的重复定位精度指在同一工况下机器人以相同位姿重复运动至一点时的偏差情况。作为示教编程条件下一项重要指标，机器人重复定位精度受到具体工况下温度、湿度、载荷等复杂因素的影响［10］。为了提高机器人路径规划的精确性，需要考虑具体工况下机器人重复定位精度。通过固定在测量平台上的三个位移传感器，可以获得机器人末端执行器搬运物块到达指定点时在x、y、z三方向上的偏差值。通过重复试验获取偏差值数据，可以得出机器人实际码垛任务工况下重复定位精度参考值。

本实验平台选用SGC-W10 微位移光栅传感器，有效量程10mm，分辨率1 μm。鉴于机器人说明书给出重复定位精度参考值为±0.08mm，本实验平台精度可以满足需求。传感器输出TTL 方波，通过RS235 串口与PC 通讯，在Matlab 环境下调用Data Acquisition 数据采集工具箱完成对传感器信号的采集和处理，如图6 所示。

图6 重复定位精度实验平台实物图片

通过100 次重复试验，获取末端执行器三维空间内偏移情况，见图7。对实验数据分析可得出实际工况下机器人重复定位精度为±0.1mm，这一结果与机器人说明书给出的参考值大致相符。

图7 机器人末端执行器空间偏移量散点图

3.2 码垛路径关键点的选取

轨迹规划既可以在笛卡尔空间进行也可以在关节空间进行。关节空间的轨迹规划是以关节角度的函数来描述机器人的轨迹的，也就是说机器人末端执行器的运动轨迹是由关节变量直接确定的，所以在关节空间中进行轨迹规划容易简单，在满足运动学和动力学约束的条件下通过插补算法可以得到关节的轨迹。并且，在关节空间进行轨迹规划可以避免运动中出现奇异点和机器人冗余问题［11］。但是，关节空间内轨迹规划由于对机器人末端执行器的实际运动位置没有直观明显的显示，很难清楚的获取末端执行器的实际位置和运动路径，对于本文研究的码垛作业，由于工作单元内存在障碍物，对末端执行器任务过程中瞬时位姿要求较高，首先需要在笛卡尔坐标空间进行路径设计，进而将设计期望轨迹中的关键点返回到关节空间，实现对关节变量的控制，最终在关节空间内完成轨迹规划。

在整个码垛任务实现过程中，在工作单元内有4 个工作点Q1、Q2、Q3、Q4。机器人末端执行器从初始位置Q0出发，经过趋近点Q1到达Q2，抓取物块后退回Q1，再由Q1经趋近点Q3到达终点Q4，最终完成对物块的码垛。由于机器人末端执行器采用吸盘完成抓取，具有一定的柔性，结合试验获取的重复定位精度参考值，在路径设计中将抓取点设定低于物块上表面0.5mm，使吸盘与物块紧密接触，确保抓取成功。在码垛过程不与工作单元内其他物块发生碰撞的前提下，给定末端执行器初始位置及依次到达的位置坐标如下:

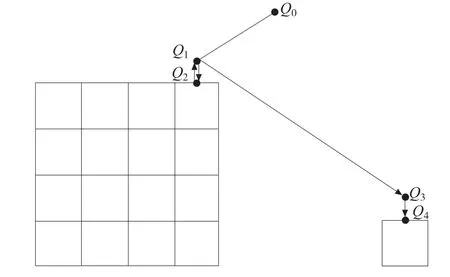
图8 码垛任务关键点选取示意图

上述位置坐标在基坐标系x0y0z0中的矢量为qi，末端执行器在运动过程中位移矢量分别为

设定末端执行器运动时间为50s，对末端执行器在笛卡尔空间内运轨迹进行仿真。依据选定的关键点，调用transl 函数将坐标返回为齐次变换矩阵，再调用ctraj 函数计算笛卡尔空间内轨迹。末端执行器完成码垛任务到达轨迹末端见图9。

末端执行器依次通过选取关键点过程中在x、y、z方向位移变化情况见图10。

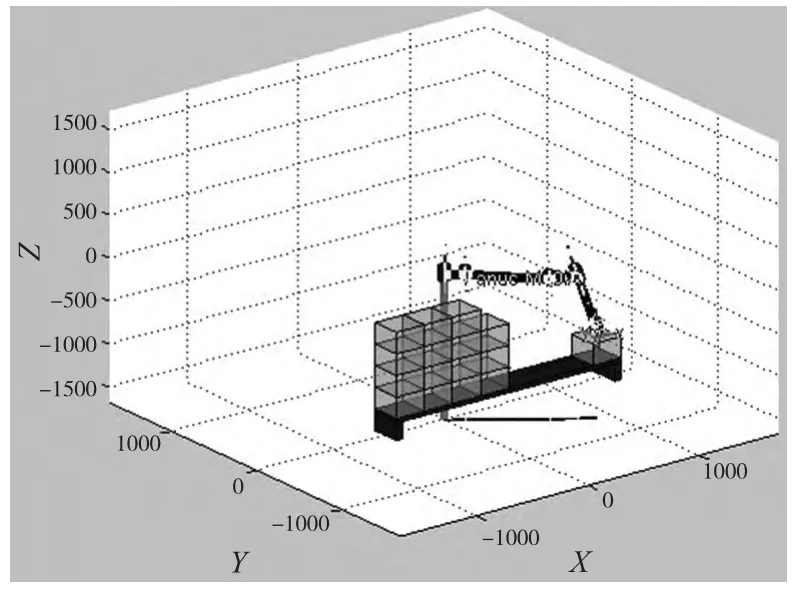
图9 M-10iA 机器人码垛任务完成效果图

图10 末端执行器各向位移变化随时间曲线

仿真结果显示，末端执行器在笛卡尔坐标系内依次通过选定的关键点，轨迹平滑，所设计的这一码垛路径可行。

3.3 关节空间内的轨迹规划

关节空间内的轨迹规划关键在于对运动学模型逆解的求解，根据笛卡尔空间内标定的末端执行器期望关键点，将整体轨迹分段分别反求出机器人各关节转角位移、速度与加速度。在Matlab 环境下使用Robotics 工具箱进行逆运动学求解，得到各关节运动学变量。由关节空间内变量变化情况可以对末端执行器轨迹合理性进行验证。各关节角位移、角速度及角加速度分别见图11、图12、图13。

对6 个关节角运动学参数进行分析，可见根据在笛卡尔空间内规划的轨迹完成码垛任务过程中，各关节角位移平滑，角速度变化幅度较小，参照M-10iA 机器人说明书参数，可以确定机器人关节角处于安全范围以内。由于机器人逆运动学中逆解的多重性问题，实现到达某一特定位置的方式很多，本文规划的这一轨迹整个运动过程平稳，可以满足码垛作业的实际需求。末端执行器返回初始位置的轨迹规划方法与前述相同，不再赘述。

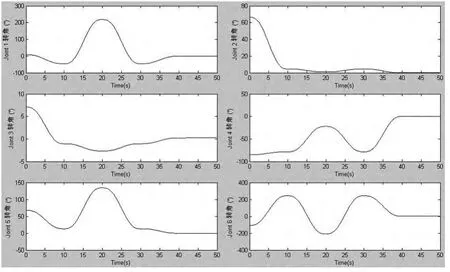
图11 码垛任务中各关节(Joint1—6)角位移随时间变化曲线

图12 码垛任务中各关节(Joint1—6)角速度随时间变化曲线

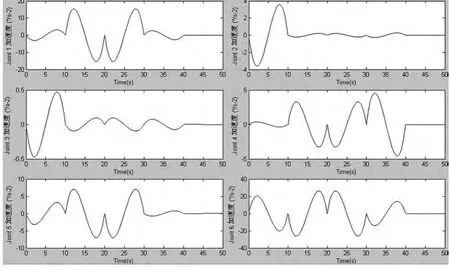
图13 码垛任务中各关节(Joint1—6)角加速度随时间变化曲线

3.4 后续码垛任务的轨迹递推

当完成首个物块码垛任务后，本工作空间内物块布局发生变化。参照码垛单元模型，在笛卡尔空间内对前述码垛任务关键点进行平移，进而对后续轨迹完成规划。为了避免干涉，后续物块抓取结束后均需返回Q1点。后续码垛任务规划示意见图14。

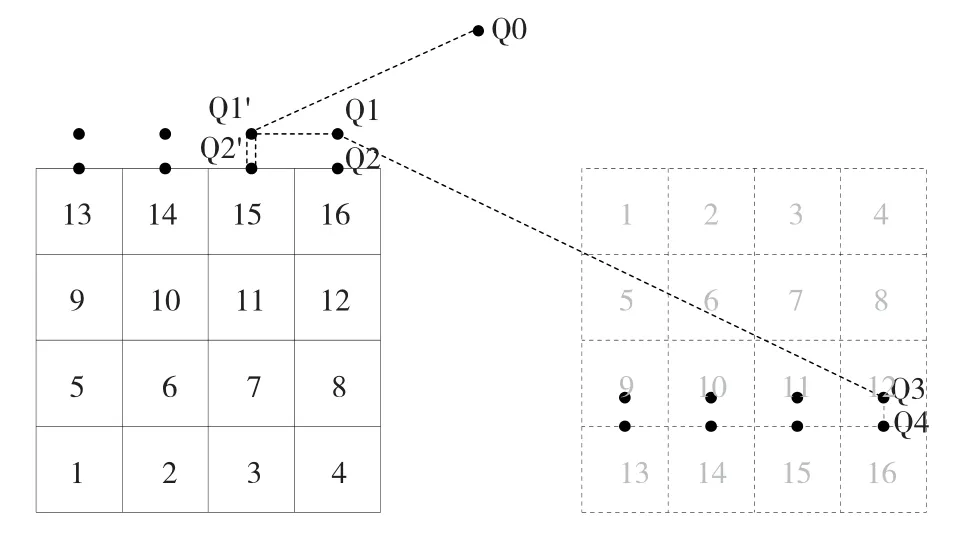
图14 后续码垛任务规划示意

依照模块化设计思路，在机器人编程过程中，可以将每一个物块的码垛过程独立保存为一个子程序，通过顺序调用这些子程序完成全部码垛任务。

4 结论

(1)在MATlAB 软件环境下依据D-H 参数法，结合实际工业机器人连杆及转角参数建立的运动学模型能达到很好的动态仿真效果。本文在此基础上对码垛工作单元整体进行的运动学仿真，具有较大的柔性，可以适应多变的实际工况。依据码垛单元整体运动学模型，可以便捷地在笛卡尔空间内直观地完成末端执行器路径设计，并返回关节空间控制各关节转角、角速度、角加速度，最终完成轨迹规划。

(2)相对于通过机器人示教盒在线示教再现编程方法完成码垛任务轨迹规划，这一动态仿真基础上的轨迹规划实现了对操作方案的预先设计，较好地消除了实际操作中操作者素质、经验等复杂因素对编程准确性的影响，降低了发生碰撞事故的危险，提高了复杂任务轨迹规划的效率，为机器人实际应用中的编程提供了有益的参考。

［1］蔡自兴.机器人学［M］. 北京:清华大学出版社，2009.

［2］孟国军.工业机器人离线编程系统关键技术的研究［D］.武汉:华中科技大学，2011.

［3］张卫荣.M-10iA 型FANUC 机器人控制系统研究与应用［D］.合肥:合肥工业大学，2012.

［4］Richard S. Hartenberg and Jacques Denavit. A Kinematic Notation for Lower Pair Mechanisms Based on Matrices［J］.Journal of Applied Mechanics，1955，77:215 -221.

［5］杨丽红，秦绪祥，蔡锦达，等.工业机器人定位精度标定技术的研究［J］.控制工程，2013，20(4):785 -788.

［6］韩建海，吴斌芳，杨萍，等.工业机器人［M］.武汉:华中科技大学出版社，2009.

［7］Corke P. I.A Robotics Toolbox for MATLAB［J］.IEEE Robotics and Automation Magazine，1996，3:24 -32.

［8］Joel S. Voxel function ［EB/OL］. MATLAB Central，file exchange，2003.

［9］XIAOYUN DENG. Robot Workcell Modeling and Collision Detection with MATLAB Robotics Toolbox ［D］. Master of Science Thesis，Tampere University of Technology，2012.

［10］胡毅，费业泰，程文涛.关节式坐标测量机热变形误差及修正［J］. 机械工程学报，2011，47(24):15 -19.

［11］刘亚军，黄田.6R 操作臂逆运动学分析与轨迹规划［J］.机械工程学报，2012，48(3):9 -15.