基于垂直两点法的电主轴回转精度分析*
2014-06-29沈鸿波张啸飞张丽秀吴玉厚
陆 峰,沈鸿波,张啸飞,张丽秀,吴玉厚,张 珂
(沈阳建筑大学 交通与机械工程学院,沈阳 110168)
0 引言
众所周知,先进制造技术是推动国家经济发展、提高国家综合竞争能力的重要手段。随着高速、精密机床的发展,在金属切削加工过程中,电主轴的回转精度已经成为加工精度的关键因素[1-3],它直接影响零部件的表面精度和形位公差[4]。电主轴回转误差的定义是指:主轴的实际回转轴线相对于理想回转轴线的相对位移[5],因此电主轴的回转误差包括三部分:纯轴向运动、纯径向运动和纯倾角运动。而纯轴向运动对于电主轴的回转误差几乎没有影响,所以本文所讨论电主轴的回转误差只包括后两种。
近几年国内外有关主轴回转误差测量的技术研究较多。其中,Eric 等分别运用反转法进行了纳米级回转精度测量,总结了电主轴回转精度纳米级测量中应该注意的问题[6]。Grejda Robert 等采用反向法误差分离方法,使用纳米级的自动反转式气浮转轴进行圆度误差测量,分离误差的结果和多步法相比小于1nm[7]。而我国,沈阳机床的刘启伟应用三个位移传感器和一个转速传感器对车削加工中心主轴的混合误差进行测量,并且利用最小二乘圆心的方法评定回转误差[8]。湖南大学李想通过对切削机床主轴的回转精度测量,对三点法圆度误差分离技术的参数选择及形状失真进行了综合分析和优化[9]。本文对三点法的分离误差的理论进行数学简化得到垂直两点法误差分离理论。但是简单的垂直两点法无法将传感器安装的误差分离出来,对于回转精度不高的主轴可以忽略其影响。但是对于高回转精度的精密电主轴,混入的形状误差或安装误差的影响是不可以忽视的,这些误差有时甚至会掩盖掉微小的电主轴回转误差,所以本文寻找有效的误差分离方法将其从采集的数据中准确地分离出去。并结合实验结果对影响回转误差的因素进行了理论分析。
1 测试系统原理及实验方案
1.1 测试系统原理
两点测量法是根据三点测量法将三个传感器中的两个传感器合并,此时三点法就演化成两点测量法。三点测量法的测量原理是使用三个同样的传感器按照一定角度垂直布置被测标准棒的同一截面上对主轴误差进行测量。但是此方法要求三个传感器安装的位置精度高,所以给安装调试造成麻烦,加大了实验的成本,而且无论装配人员的技术水平多好,都不可避免的带来偏心误差。因此为了降低测量装置的安装难度,所以选择垂直两点法进行测量,装配容易,能很容易地测得电主轴混合误差,并能够分离出电主轴回转误差中混入的电主轴偏心误差,从而直观地显示回转误差的轨迹图。
1.2 实验方案
图1、图2 分别回转误差测试的实物图和二维图,图3 为测试系统的方框图,在主轴的轴端位置安装高精度的标准棒,把两个非接触式的传感器(传感器型号:LK-H0200、精度:0.001mm)按照垂直角度布置在同一垂直平面内,利用传感器和标准棒之间的位移变化来检测电主轴包括圆度误差和回转误差的混合误差信号。然后将传感器采集到的数据导入电脑中,利用MATLAB 程序进行误差分离的运算,将分离后的结果绘制成圆图。

图1 电主轴回转误差测试实物图
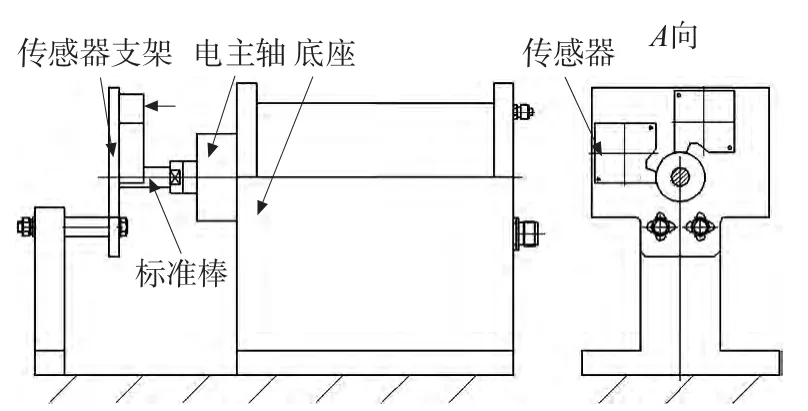
图2 电主轴回转误差测试装置二维图
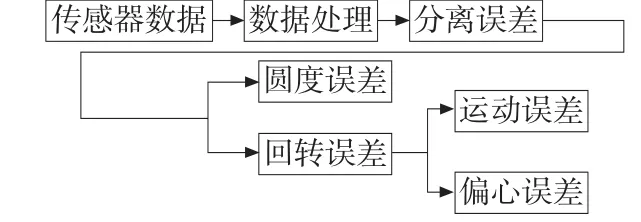
图3 测试系统框图
2 垂直两点法误差分离模型
垂直两点法分离误差模型是根据三点法演化的,三点法圆度误差分离技术是由日本学者青木保雄和大园成夫在1966 年提出来的,该方法利用频谱技术把圆度误差与回转误差分离开来。
如图4 所示,为三点法[10]分离圆度误差和回转误差的原理图,以传感器S0、S1、S2检测轴线的交点O为坐标原点建立平面直角坐标系XOY。
设:r(θ)为被测零件在θ 处的圆度形状误差。x(θ)、y(θ)分别为测量回转轴在θ 处回转运动误差在坐标系内XOY坐标轴上的分量,α、β 分别为传感器S1、S2与传感器S0之间的夹角[11]。测量时,传感器固定,被测零件由回转工作台带动其作回转运动,设S0(θ)、S1(θ)、S2(θ)分别为传感器S0、S1、S2的信号输出,则可得三个传感器中包含的数据为:
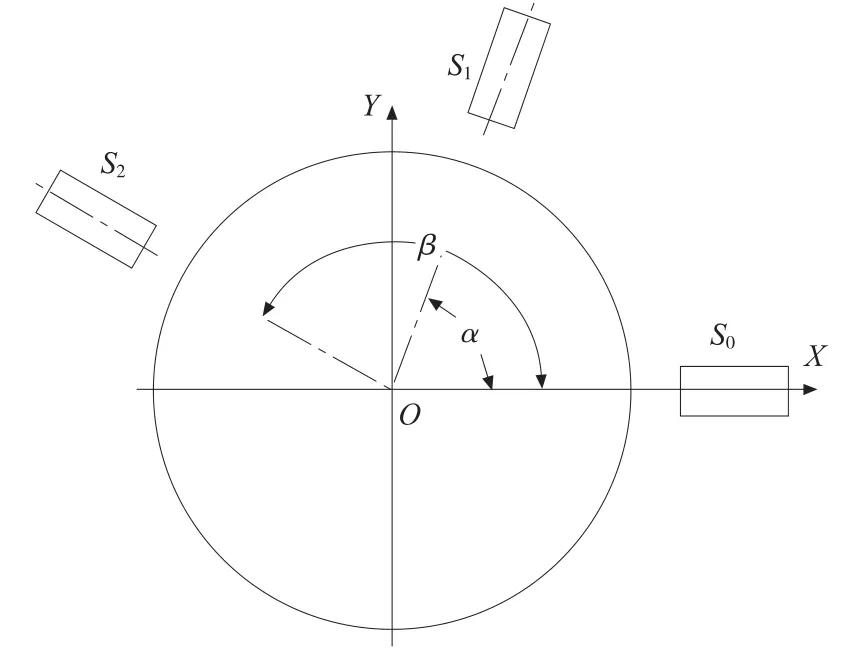
图4 三点法分离误差原理图

引入传感器的标定系数c0、c1、c2,则上面(1)、(2)、(3)式分别乘以c0、c1、c2得到:
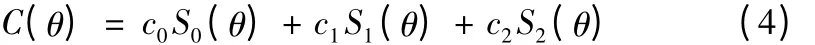
根据(4)式展开,若要分离出圆度误差r(θ),则需要x(θ)、y(θ)前的系数为零,则得到:
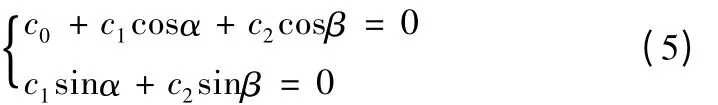
此线性方程组有无穷多解,取c0=1 ,得到一组特解为:
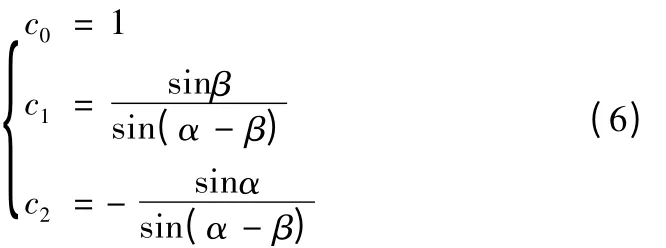
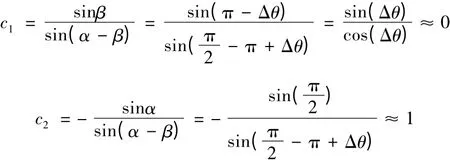
当c1=0 时,传感器S1的输出信号在信号的加权中占有很小的比重,可以忽略不计。那么,三点法圆度误差分离技术就演化成了垂直两点法圆度误差分离技术。(4)式就可以写成:
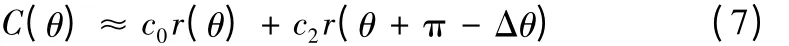
将(7)式离散化得到:
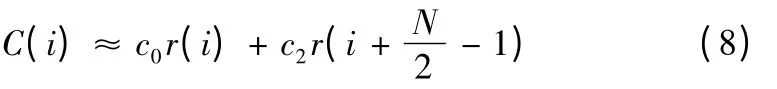
对(8)式进行离散快速傅里叶变换(FFT),得到:
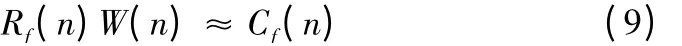
Rf(n)为时域上电主轴的圆度误差r(i),Cf(n)为时域上圆度误差和回转误差的混合信号;W(n)为权函数,如下:
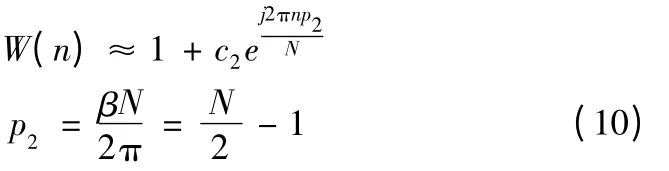
当W(n)≠0 时,有:
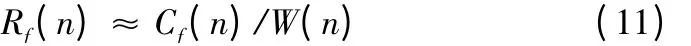
对(11)式进行离散快速傅里叶逆变换(IFFT),得到:

将(12)式代入(1)、(2)式可以得到:

因此根据(13)式可以得到X、Y两个方向的回转误差x(θ)、y(θ)中包含着电主轴自身绕回转轴转动的运动误差,记作δx、δy;两个传感器中心与电主轴回转中心不同心带来的偏心误差,记作:Δex、Δey;则有下列关系式:
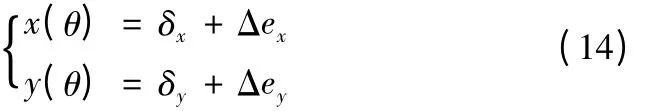
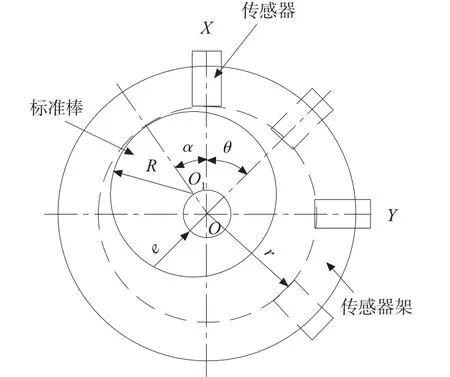
图5 系统误差消除原理图
根据图5 可知:
电主轴回转中心到标准棒的表面距离的距离Lx为:
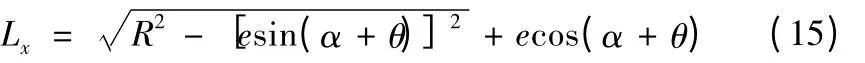
传感器架的半径r为:
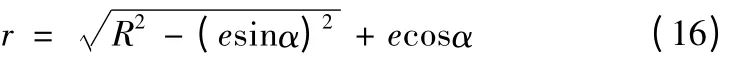
则安装偏心误差Δex为:

由于X、Y两个方向相差90°,因此Ly为:

3 测试数据分析
如图1、图2 所示的测量系统进行测量得到电主轴在(1000~20000)r/min 下X、Y方向的混合误差,图6、图7 和 图8 分 别 为7000r/min、10000r/min 和16000r/min 时的混合误差。

图6 7000r/min 混合误差
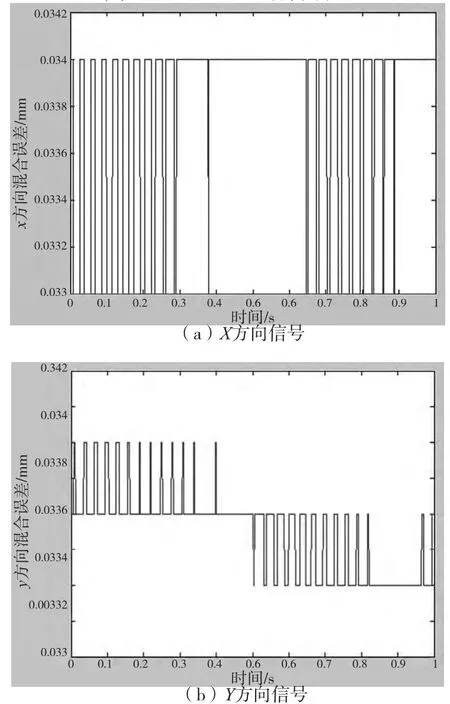
图7 10000r/min 混合误差
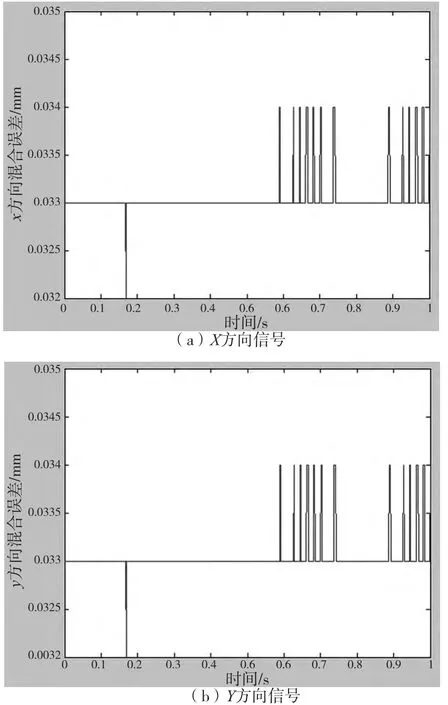
图8 16000r/min 混合误差
利用推导出的垂直两点分离误差的方法,对混合误差进行分离,得到除去圆度误差和安装偏心误差后的回转误差,图9a、9b、9c、9d、9e 和9f 对应的转速分别是 1000r/min、3000r/min、5000r/min、7000r/min、10000r/min、16000r/min 和20000r/min 时的回转误差:
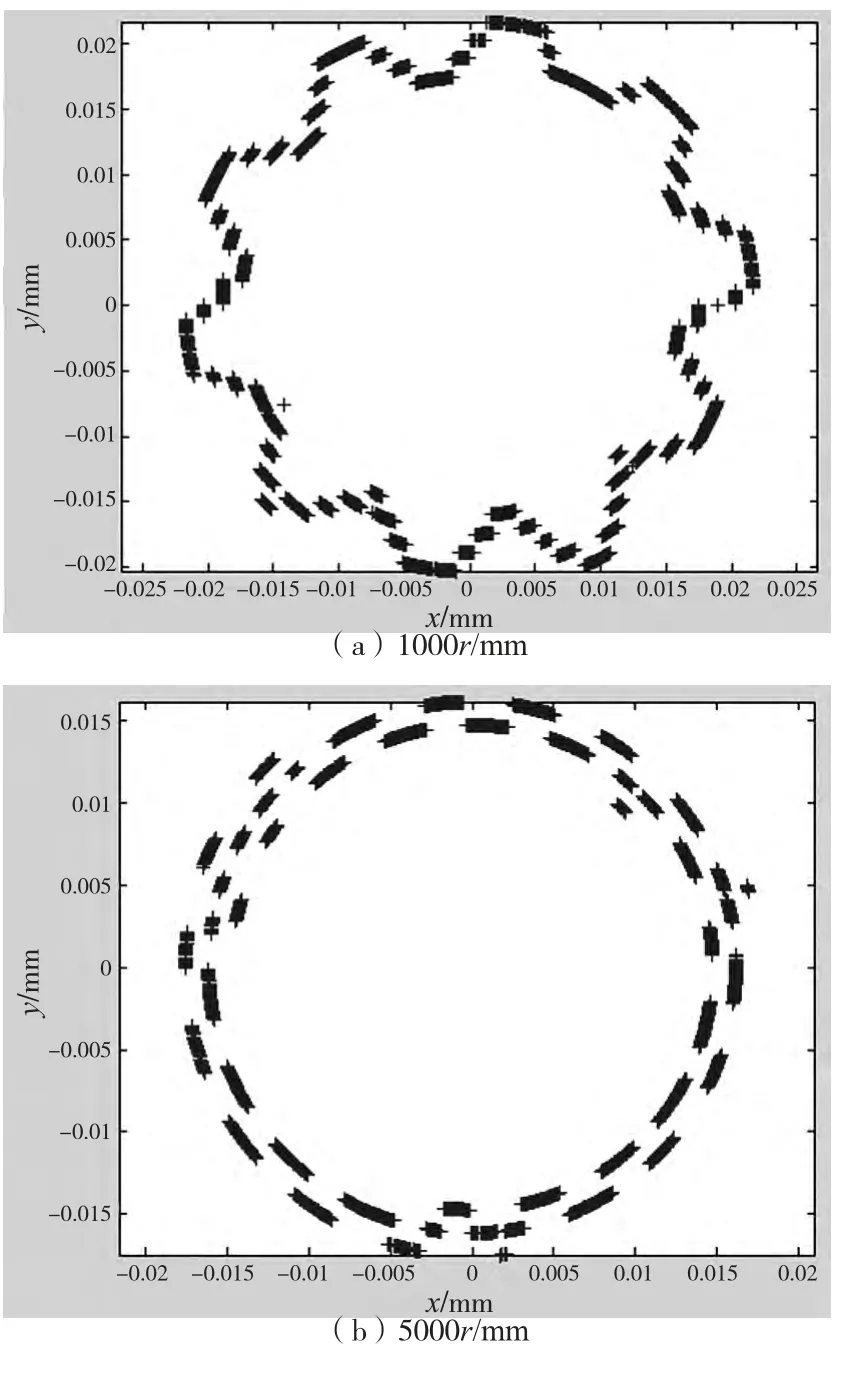

图9 分离后的回转误差
为了验证垂直两点法分离误差的正确性,使用高精度接触式的千分表测量标准棒的圆度误差,得到标准棒的圆度误差(测量的位置是与传感器测量的同一位置),得到的测量结果为(0.001~0.005)mm 之间,而通过垂直两点法分离出标准棒的圆度误差如图10所示,圆度误差为(0.002~0.005)mm,这与测量结果基本一致,从而验证了垂直两点法分离误差算法的正确性。由于去掉了一个非接触式传感器,使得测试系统安装调试都更加方便,这是垂直两点法最大的优点。
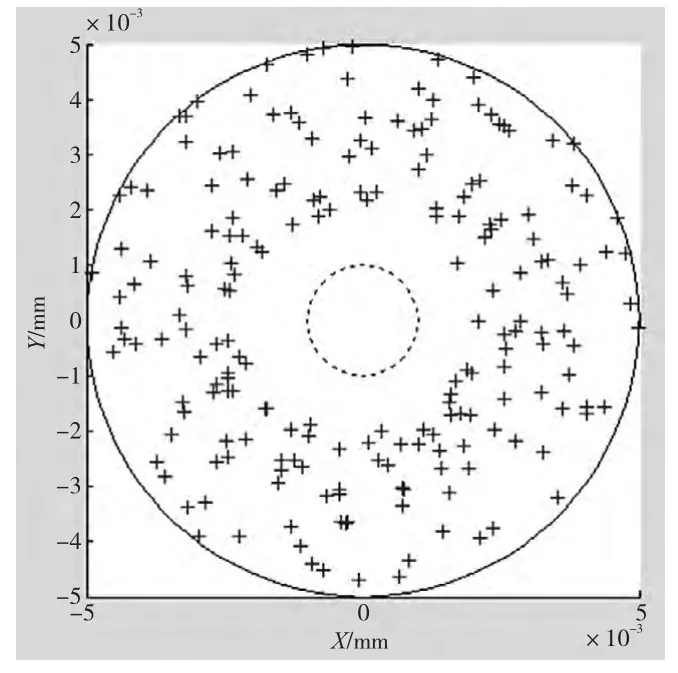
图10 分离出的圆度误差
经过垂直两点法分离后并去除偏心后的不同转速下电主轴的回转误差,如图11 所示:
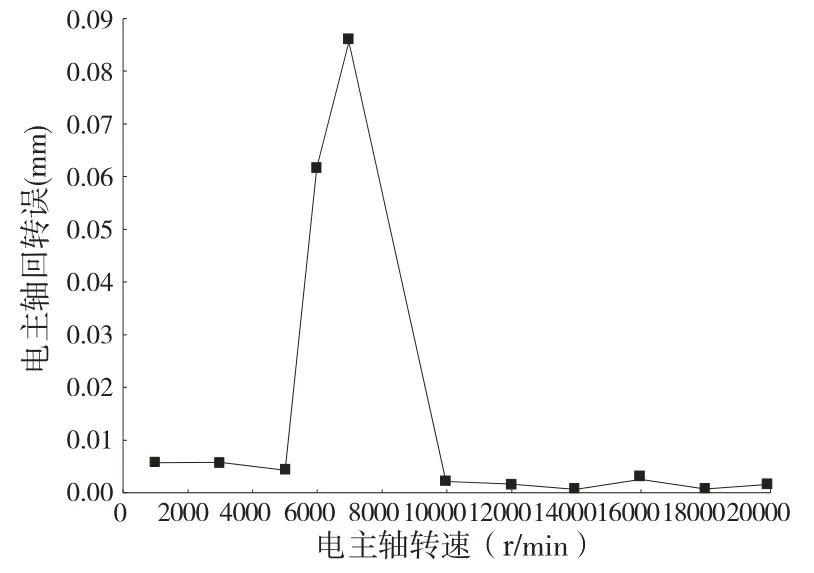
图11 不同转速下的回转误差
从分离后的结果可以看到,电主轴在(1000~3000)r/min 时的回转误差较大,因为电主轴在此转速下为电主轴刚启动时的转速,电主轴由于惯性和低频振动的原因导致回转误差在较低转速时很大;当电主轴的转速达到5000r/min 时,电主轴的回转误差减小;但是当电主轴转速达到(6000~7000)r/min 时,回转误差又继续增加,这是因为此时电主轴的转速在慢慢的接近临界转速(n=8000r/min),所以回转误差再增大;而在电主轴转速在(7000~9000)r/min 之间时,电主轴有共振现象的产生,为了避免对电主轴和实验设备的损坏,跳过了此转速;电主轴转速在10000r/min 以上时,回转误差减小而且趋于平稳,适合进行零部件的精加工。
4 结论
本文通过对三点法的简化得到垂直两点法分离误差的数学模型,而且建立了去除安装偏心的数学模型,弥补了垂直两点法无法去除偏心信号的不足。运用垂直两点法分离出电主轴的回转误差,得到了电主轴在各个转速下的回转误差的精确值,并且分析了影响回转精度的因素,这对在线监测电主轴的回转误差和控制电主轴的转速提供了重要的理论依据。
[1]吴玉厚.数控机床电主轴单元技术[M].北京:机械工业出版社,2006.
[2]伍良生,杨勇,周大帅.机床主轴径向回转误差的测试与研究[J].机械设计与制造,2009(1):107 -109.
[3]张瑜胜.电主轴在数控机床中的应用[J].机械管理开发,2011(1):137 -138.
[4]王翔.计算机辅助回转精度测量系统的研制[J].机械与电子,2006(7):41 -43.
[5]陈长浩. 主轴运动精度的测试与研究[D]. 北京工业大学,2010.
[6]Eric R.Marsh,David A.Arneson,Donald L.Martin.A comparison of reversal and multiprobe error separation[J].Precision Engineering,March 2010(34):85 -91.
[7]Grejda Robert,Marsh Eric,Vallance Ryan. Techniques for calibrating spindles with nanometer error motion. Precision Engineering. 2005,29(1):113 -123.
[8]刘启伟.主轴动态误差测试及分析[J]. CAD/CAM 与制造业信息化,2013(2 -3):80 -84.
[9]李想.面向切削工况的主轴系统回转精度及动刚度测试方法研究[D].长沙:湖南大学,2013.
[10]Ma Ping,Huang Jianjian,Li Duanneng.The Comparative Analysis about Rotational Error Separation with Three-point Method and Approximate Three-Point[J]. The International Conference on Information Engineering and Mechanical Engineering (IEME),2011,1 -5.
[11]黄斌.基于激光位移传感器的数控机床主轴径向运动误差测试方法研究[D].杭州:浙江大学,2008.
