AOCMT 机床旋转轴几何误差辨识方法的研究*

范晋伟，宋 毅，唐宇航，王志远

(北京工业大学 机电学院，北京 100124)

0 引言

随着机械制造业的发展，五轴数控机床的应用越来越广泛。五轴数控机床有着金属切除率高，加工时间短，工件表面光洁度好等优点，能够加工形状复杂，精度要求高的零件，广泛应用于航天航空、船舶、精密仪器等行业。相比传统的三轴机床，五轴机床固然有着许多优点，但是由于增加了两个旋转轴，使得机床累积的误差也不可避免的增加，因此五轴机床的整体精度不如三轴机床。五轴机床的精度由多种误差综合影响，其中几何误差是系统的，有条理的，具有重复性，并且可以测量，对几何误差进行补偿是一种低成本获得高精度的有效方法［1］。

对于五轴机床来说，其线性轴的检测已经日趋成熟和完善，而旋转轴检测则没有统一的标准，因而成为国内外学者们研究的一个侧重点。天津大学张大卫等［2］通过机床多轴联动使球杆仪完成圆弧轨迹运动，采集球杆仪的杆长变化量，由数学建模及轨迹仿真，结合误差敏感方向分析，最终分离得到影响加工精度较大的C轴四项误差。刘飞［3］设计了一种利用球杆仪进行回转轴几何误差的测量方法，这种检测模型可以避免利用标准芯棒进行间接测量而增加误差，解决了一部分回转轴由于无法安装标准棒而难于检测误差的问题。M. Tsutsumi［4-5］等考虑位置点无关误差，分别利用机床三轴和四轴同时控制来保证球杆仪做圆形轨迹运动，并通过测量的杆长变化量来辨识旋转轴误差参数，并进行仿真和实验验证，证明了其准确性。Soichi Ibaraki［6］等考虑了位置点相关误差的影响，建立运动模型，通过加工圆锥台仿真得到旋转轴的主要误差影响项，并做了实验验证。综合以上国内外的研究，大都是只考虑位置点无关误差或只考虑位置点相关误差，将二者结合起来考虑的研究并不多见。作者以AOCMT 型机床为例，同时考虑旋转轴的位置点无关误差和位置点相关误差，提出一种误差辨识方法。此方法运用球杆仪测量，从球杆仪杆长变化量和运动轨迹偏心率中分离出旋转轴8 项误差参数。

1 机床结构及旋转轴误差参数

本文以AOCMT 型五轴超精密加工机床为研究对象。该机床在XFYZ 型三轴立式数控机床工作台上叠加A、C 回转工作台构成TRTTR 型五轴立式数控机床［7］，其结构如图1 所示。对于此类机床，由于其零部件的加工以及装配的不精确以及摩擦磨损等因素作用，根据其部件的运动特性，它的旋转轴共产生与之相关的8 项误差参数。C轴与X，Y轴之间产生垂直度误差εCX，εCY，如图2 所示，C 轴旋转时产生三项线位移误差δx(γ)，δy(γ)，δz(γ)，三项角位移误差εx(γ)，εy(γ)，εz(γ)，如图3 所示。

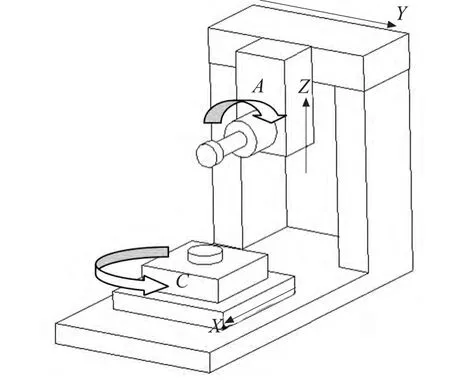
图1 AOCMT 型机床结构示意图

图2 C 轴2 项垂直度误差

图3 C 轴6 项运动误差

2 C 轴几何误差参数辨识方法

球杆仪作为一种测量仪器早期主要用于传统三轴机床圆弧运动的测量，并有助于其性能测试和定期维护。近些年球杆仪开始被各国学者用于五轴机床的检测和测量。本文利用多体系统理论建立旋转轴几何误差参数辨识模型，结合球杆仪测量原理提出了一种新的误差辨识方法。

由上述分析我们可以知道C轴共有8 项相关误差参数。球杆仪的测量方式有三种，如图4 所示，以C 转台与回转轴线交点为原点建立坐标系，为工作台端小球球心到台面的高度，为工作台端小球球心到C 轴回转轴线的距离，L为球杆仪杆长。通过控制机床两个平动轴和一个旋转轴同步运动来测量，从传感器输出信号可以读出杆长变化量。

如图4 所示，工作台端小球A 在机床坐标系的位置的齐次坐标为(Rc，0，hc，1)T，由多体系统理论可知，C轴转过γ 角，球A 在机床坐标系的位置坐标为:

图4 球杆仪三种测量方式

化简整理可得:

在不同的测量方式下，主轴端小球的位置坐标各不相同。如图4a，球B 在机床坐标系的齐次坐标为(RC，0，hc+L，1)T;同样，我们根据图4b、图4c 可知球B 位置的齐次坐标分别为(Rc+L，0，hc，1)T，(Rc，L，hc，1)T。由此我们可以知道C 轴转过γ 角，球B 在机床坐标系的位置坐标分别为:

进一步我们可以推出杆长变化量的公式:

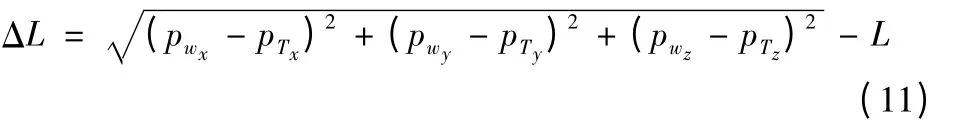
将式(8)，(9)，(10)中的坐标代入式(11)，分别化简整理可得:

对式(5)，(6)移项平方化简整理可得:

取Rc = hc =50mm，分别对8 项误差单独赋值，令εCX= εCY =0.005°，对另外6 项动态误差采取赋随机值的方法进行仿真，以确保结果的准确性。其结果如图5 所示。由此我们可以发现当εCX和εCY存在时，球A 的运动轨迹相对于理想轨迹发生偏心。而当δx(γ)，δy(γ)，δz(γ)，εx(γ)，εy(γ)，εz(γ)存在时，运动轨迹不发生偏心，只影响运动轨迹圆的半径，其中δx(γ)，εy(γ)对半径的影响程度较其它更大，这也证明了式(15)的准确性。

杆长变化量ΔL能够反应球A 运动轨迹圆的半径变化量。通过采集测量的ΔL的值，对球A 运动轨迹进行最小二乘法拟合圆，可

图5 C 轴各误差对径向圆轨迹的影响

解得球A 在坐标系相应的偏心量。本文采集径向测量方式中的杆长变化量ΔLr，解得球A 在XY 平面内的偏心量ex1和ey1，可得:

由此可以解得:

通过最小二乘法圆拟合可得出偏心量ex1和ey1的拟合值，将εCX= εCY =0.005°，hc =50mm代入式(16)，得到偏心量的计算值，二者对比如下表:

表1 拟合值与计算值的对比

由表1 所示，拟合值和计算值之间只有0.04μm的差距，因此式(17)是准确的。由式(12)，取不同的距离Rc1，Rc2相同的高度hc1，测量可得不同的杆长变化量ΔLs1，ΔLs2，结合式(16)进一步推出:

由式(13)，取高度hc1，测得杆长变化量ΔLr1，结合式(17)可解得:

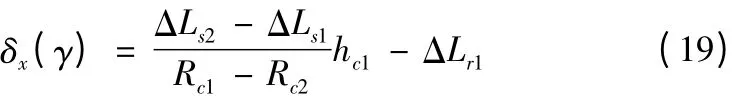
由式(14)，取不同的距离Rc1，Rc2，相同的高度hc1，测量可得不同的杆长变化量ΔLt1，ΔLt2，进一步推出:

由式(14)，取相同的距离Rc1，不同的高度hc1，hc2，测量可得不同的杆长变化量ΔLt1，ΔLt3，结合式(17)进一步推出:

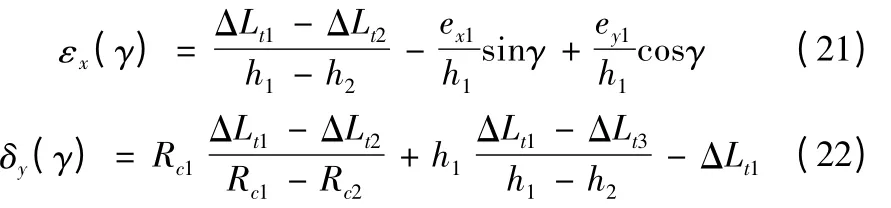
至此，C 轴8 项误差全部辨识完毕。

3 总结

本文以AOCMT 五轴机床为例，通过机床两个平动轴和一个旋转轴同时运动，运用球杆仪对其旋转轴C轴进行测量，提出了一种准确高效的误差辨识方法。由于篇幅有限，实验验证将在后续的文章中补充。该方法通过3 种测量模式的6 次测量，结合球杆仪运动轨迹偏心原理可以将包含位置点无关和位置点相关共8 项误差全部辨识出来。相比只考虑位置点无关或只考虑位置点相关误差，该方法具有新颖性和实用性，且通过仿真验证证明其切实可用，为国家数控机床精密化提供了参考性意见。

［1］Jian-xiong Chen，Shu-wenLin，Bing-weiHe.Geome -tric error measurement and identification for rotary table of multi-axis machine tool using double ball bar. International Journal of Machine Tools ＆ Manu -facture，77(2014):47 -55.

［2］张大卫，商鹏，田延岭，等.五轴数控机床转轴误差元素的球杆仪检测方法［J］. 中国机械工程，2008，19(22):2737 -2741.

［3］刘飞.五轴数控机床回转轴的误差检测技术研究［J］.机械工程与自动化2009(4):133 -135.

［4］M.Tsutumi，A.Saito，Identification and compensation of systematic deviations particular to 5-axis machining centers［J］.International Journal of Machine Tools ＆ Manufacture 43(2003):771 -780.

［5］Masaomi Tsutsumi，Akinori Saito，Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements［J］. International Journal of Machine Tools ＆Manufacture 2004 (44):1333 -1342.

［6］Cefu Hong，Soichi Ibaraki，Atsushi Matsubara，Influence of position-dependent geometric errors of rotary axes on a machining test of cone frustum by five-axis machine tools［J］.Precision Engineering 2011 (35):1 -11.

［7］李圣怡，戴一凡，尹自强. 精密和超精密机床精度建模技术［M］. 长沙:国防科技大学出版社，2007.

［8］Kwang-Il Lee，Seung-Han Yang，Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar［J］. International Journal of Machine Tools ＆ Manufacture 2013 (70):45 –52.

［9］Dong-Mok Lee，Zankun Zhu，Kwang-Il Lee，et alIdentification and Measurement of Geometric Errors for a Five-axis Machine Tool with a Tilting Head using a Double Ball-bar［J］. International journal of precision engineering and manufacturing 12(2):337 -343.

［10］M. Sharif Uddina，Soichi Ibarakia，Atsushi Matsubaraa.Prediction and compensation of machining geometric errors of five-axis machining centers with kinematic errors［J］. Precision Engineering 2009 (33):194 -201.

［11］蔡晓华.数控机床旋转轴的误差检测和辨识［D］.上海:上海交通大学，2013.

［12］孙惠娟，蒋红海，殷国富.基于机器视觉的五坐标机床旋转轴误差检测方法［J］. 农业机械学报2013，44(8):293 -298.