EMD 方法和倒频谱在齿轮箱故障诊断中的应用

刘自然，熊 伟，颜丙生，甄守乐，王律强

(河南工业大学 机电工程学院，郑州 450007)

0 引言

齿轮箱的升降速过程包含了丰富的状态信息，一些在平稳运行时不易反映的故障征兆可能会充分地表现出来［1］。但齿轮箱的升降速过程信号比平稳过程信号复杂得多，常规的频谱分析方法不适用。为了处理非平稳信号，短时傅里叶变换、Winger-Ville 分布和小波分析等卓有成效的信号分析方法逐渐提出并应用于故障诊断中。但这不表明上述矛盾完全解决，因为几乎所有的时频分析方法都以傅里叶变换为最终理论依据［2］。而EMD 方法从根本上摆脱了傅里叶变换的局限性，具有很高的信噪比，非常适用于非平稳过程。近年来，在齿轮箱故障诊断中，EMD 技术与其它信号处理方法相结合得到了广泛的应用，包括傅里叶变换、时间序列分析、支持向量机等。而本文提出一种基于EMD 和倒频谱结合的齿轮箱故障诊断方法，能够有效提取出齿轮箱的振动特征。

1 EMD 基本理论

美籍华人Norden. Huang 等人创造性的提出本征模态函数的基本概念以及将任意信号分解为本征模态函数(IMF)的EMD 分解。EMD 方法是基于信号的局部特征尺度，能够把复杂信号分解成固有模态函数，其实质是对非平稳信号进行平稳化处理，得到一系列不同特征尺度的时间序列，每一个时间序列对应一个固有模态函数。得到基本模态函数需要满足两个条件:在整个数据段内，极值点的数量(包含极大值和极小值)与过零点的数量相等或者相差不能超过一个;除此之外，在任何一个时间点，其局部极大值所确定包络线和局部极小值确定包络线的均值为零。将原始信号分解成IMF 的方法如下:找出x(t)的极值点，并分别拟合出原数据的上、下包络线;求上、下包络线的均值曲线m1(t);将原数据序列x(t)减去该平均包络，得到一个新数据序列:

第1 个IMF 分量代表原始数据中最高频的组分，通过检测h1(t)是否满足基本模态函数的两个基本条件，如果满足，就停止分解;如果不满足，则把h1(t)当作待处理信号，重复上面的操作，直至满足基本模态函数的两个基本条件。

这样，就把一个数据分解成若干固有模态函数和残余量之和。则

对每个固有模态函数ci(t)作Hilbert 变换得:

构造解析函数

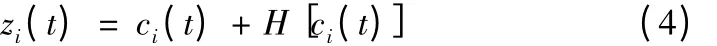
可以得到幅值函数

相位函数

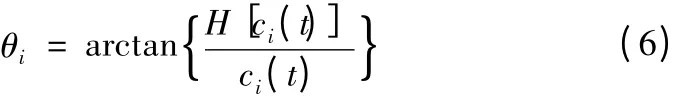
并可以进一步得到瞬时频率

从上面分解过程可知:EMD 可以将原始信号分解成若干个基本模态函数，这些模态函数包含各种不同的频率成分，而剩余分量r(t)表示了原始信号的中心趋势。

2 EMD 方法与倒频谱结合的分析技术

倒频谱分析也称为二次频谱分析，是近代信号处理中的新技术。它可以处理复杂频谱中的周期成分，其实质是对其功率谱密度函数取对数，然后进行傅里叶变换并取平方，则可以得到倒谱函数Cp(q)。其基本公式如下:

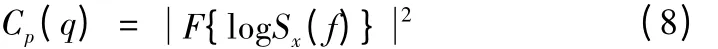
其中:Sx(f)为功率谱密度函数，q为倒频率。

而在工程上常用的是其开方形式，即

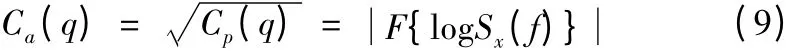
Ca(q)称为幅值倒谱，简称倒谱。

倒频谱可以检测复杂信号频谱上的周期结构，对于同族或异族谐频、多成分的边频等复杂的信号分析以及识别非常有效。

基于以上分析，本文结合EMD 分解和倒频谱的优势，提出一种基于EMD 分解和倒频谱结合的齿轮箱故障诊断方法。首先对齿轮箱振动信号进行EMD 分解，然后对复杂的基本模式分量进行倒频谱处理，有效提取出齿轮箱的振动特征。本文方法的流程图如图1 所示:

图1 齿轮箱故障诊断流程图

3 试验实例分析

3.1 试车台齿轮箱试验简介

本实验来源于某横向项目“某试车台振动测试系统与控制系统设计”，试验齿轮箱内部传动系统:采用二级传动，第一级为锥齿轮正交轴传动，传动比为3.05;第二级为单斜齿平行轴传动，传动比4.31。六只加速度传感器(采用美国PCB 型号M230C18 和M353B18)，4 号传感器安装在齿轮箱上的竖直方向，采样频率为10240Hz。

经计算，当电机的转频为12.0Hz 时，中间轴的转频为36.6Hz，输出轴的转频为157.1Hz，一级齿轮啮合频率为768.0Hz，二级齿轮啮合频率为4571.4Hz。选取10240 点，对实测振动数据，首先对样本数据进行EMD 分解，然后对包含丰富信息的IMF 分量进行包络谱分析。

3.2 数据格式转换简介

试车台所采集数据的格式为TDMS，而分析数据的程序是用Matlab 编写的，由于Matlab 不能直接读取TDMS 格式的数据，影响运用Matlab 进行分析和处理。Excel 作为最常见的电子表格形式，NI 公司提供了一种工具箱TDM Excel Add -In Tool，它使Excel 表格可以打开TDMS 格式的数据。安装该工具箱后，打开Excel 表格，在表格的工具栏上会出现TDM Importer，如图2 所示。点击工具栏上的Importer 按钮，就可打开文件搜索窗口，在指定的文件夹中就可以打开TDMS格式文件。

图2 TDM Importer 工具栏

3.3 齿轮箱超限诊断

齿轮箱实测信号的时域波形图及傅氏频谱如图3所示。

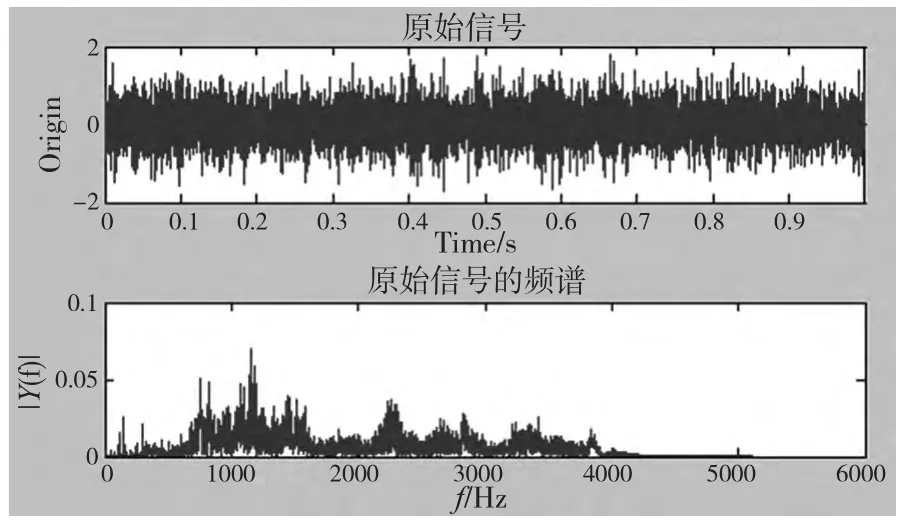
图3 齿轮箱超限的时域图与频谱图

用EMD 方法对振动信号分解得到13 个IMF 分量和1 个残余分量，由于前三个IMF 分量已包含了振动信号的主要成分，因此主要对前三阶成分进行分析。如图4 为前3 个IMF 分量与其包络谱。

图4 前三阶IMF 分量与包络谱

从第一阶IMF 频谱我们可以看到明显看见谱线周围有明显成簇的边频成分，因此我们想到对该信号进行倒频谱分析，如图5 所示。

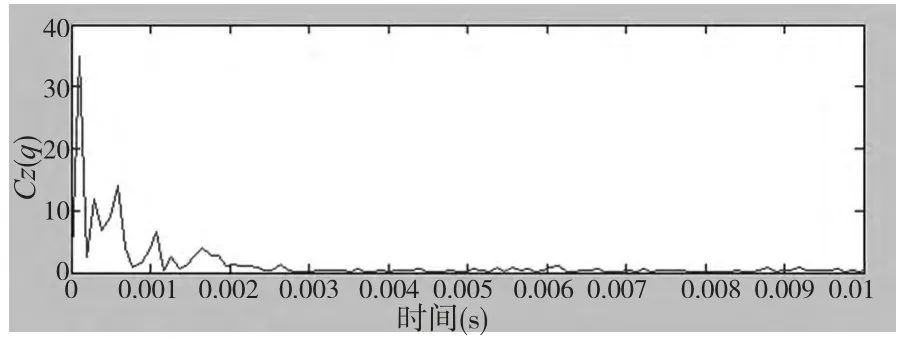
图5 第一阶IMF 分量的倒谱图

从倒频谱图我们可以看见，有两条清晰的谱线，分别对应0.632ms 和1.274ms。后者为前者的两倍，对应的频率分别为1582.2Hz 和784.9Hz。1582.2Hz 对应以及啮合频率的2 倍，齿轮可能存在不均匀的加工误差。但是需要注意，倒频谱图中的横坐标为倒频率，并不直接对应特征频率，而是通过计算得出故障的特征频率。

从图6 我们可以清楚的看到第三阶IMF 分量时域图有明显的调制现象，对其进行包络谱分析，如图7 所示。

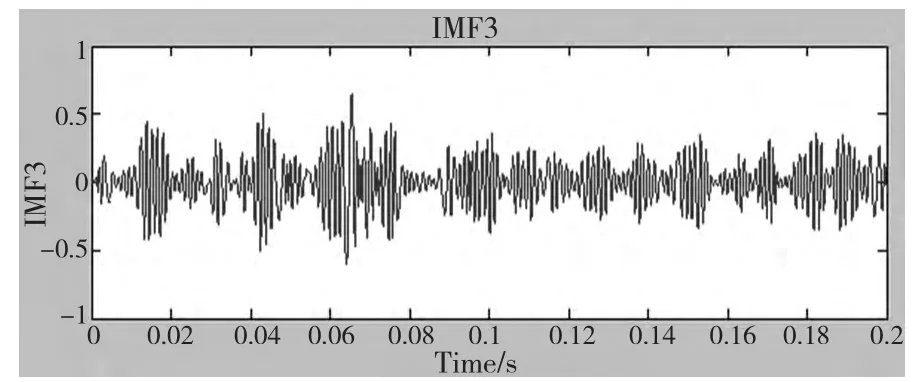
图6 第三阶IMF 分量时域图

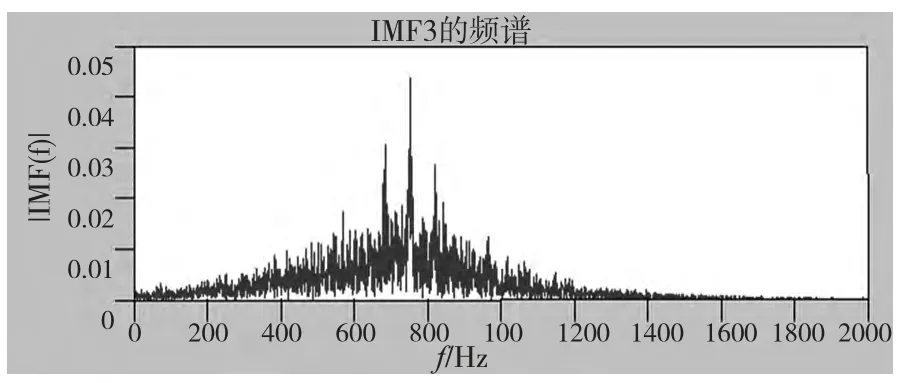
图7 第三阶IMF 分量包络谱

从包络谱中我们可以清楚的看出752.5Hz 的中心频率和72Hz 的调制边频带，通过对比我们可以发现，752.5Hz 对应一级齿轮啮合频率，72Hz 对应中间轴的转频的二倍频，由此我们可以通过EMD 和包络谱来判断齿轮箱的运行情况，对于非正常振动的齿轮箱，通过EMD 方法可以对信号进行解调，寻找出超限报警的原因。

值得注意的是，EMD 分解的包络谱图7 与所示的傅里叶频谱图3 相比，我们可以发现:在傅里叶变换的频谱图上，对于一级齿轮啮合频率附近的边频带被强大的背景噪声或干扰信号所淹没，而在经过EMD 分解的包络谱图7 上，我们可以清晰地看到一级齿轮啮合频率的边频带;在图4 的第一阶IMF 包络谱中，有明显的成簇成分，提取不出明显的振动特征，而在图5 所示的倒频谱图上，我们则可以清晰看见啮合频率及其二倍频。因此，EMD 方法和倒频谱结合能够有效提取出齿轮箱的振动特征。

4 结论

基于信号的局部特征时间尺度的EMD 分解，能够把平稳或非平稳信号分解成有限个平稳的固有模态函数IMF，通过EMD 方法得到的基本模式分量(IMF)具有明显的调幅特性，可以有效实现背景和噪声信号的分离。而包络谱是故障分析常用的方法，但由于噪声信号和干扰成分的存在，使得特征频率出现偏差，甚至淹没于噪声信号里，而倒频谱可以检测复杂周期信号频谱上的周期结构，分离和提取密集泛频谱信号中的周期成分。通过试验说明，将EMD 方法和倒频谱结合进行齿轮箱故障诊断是非常有效的。

［1］刘自然，甄守乐，颜丙生，等.基于TDMS 的海量振动数据快速存储和查询虚拟系统［J］. 组合机床与自动化加工技术，2013(9):88 -91.

［2］侯亚丁，陈宏，赵营豪，等.基于IMF 包络谱和倒频谱的滚动轴承故障诊断［J］.振动与冲击.2012:60 -63.

［3］羊初发.基于EMD 的时频分析与滤波研究［D］.成都:电子科技大学，2009.

［4］李辉，郑海起，杨绍普.齿轮箱起动过程故障诊断［J］.振动、测试与诊断.2009，29(2):167 -170，240.

［5］郭楠，潘宏侠，孙黎明.基于EMD 细化包络谱分析在轴承故障诊断中的应用［J］. 煤矿机械，2010，31 (2):206 -208.

［6］韩捷，张瑞.旋转机械故障机理及诊断技术［M］.机械工业出版社，1997.

［7］杨宇，于德介，程军圣.基于经验模态分解的滚动轴承故障诊断方法［J］. 中国机械工程，2004，1 (10):908 -911.

［8］钟佑明，秦树人，汤宝平.希尔伯特-黄变换中边际谱的研究［J］. 系 统 工 程 与 电 子 技 术，2004，26 (9):1323 -1326.

［9］侯铁军，石成江，孙敬敬.基于倒频谱分析的齿轮故障诊断［J］.煤矿机械，2011，32(11):269 -271.

［10］石文磊，陈兴明，袁海龙. 基于EMD 和Hilbert 包络谱的滚动轴承故障诊断［J］. 机械工程与自动化，2010(5):108 -110.