基于可靠度的隧道行车视距影响因素分析

孙 璐 秦玉秀 游克思 崔相民 Mostafa Ardakani

(1东南大学交通学院，南京210096)

(2美国Catholic大学土木工程系，华盛顿特区20064)

(3上海市政工程设计研究总院(集团)有限公司，上海200092)

(4山东省公路检测中心，济宁270000)

隧道内由于光线相对暗淡以及封闭的空间结构，相对于地面道路，其行车视距对交通安全的影响更加突出.尤其是在曲线路段，受侧墙及顶板影响，驾驶人很难判断前方道路情况及道路线形整体走向，导致这些路段成为事故多发路段，因此研究隧道内的行车视距对提高隧道交通安全具有重要意义.

已有研究表明行车视距受运行速度、路面摩擦系数、曲线半径、侧向净宽等多种因素影响［1］，但目前在分析这些影响因素时，多采用确定性的分析方法，即将车辆运行速度、路面摩擦系数、驾驶人反应时间等这些重要参数作为确定性变量，忽略变量的随机性和不确定性，通过计算获得唯一确定的视距值，与相关规范作比较，进而判断是否满足设计要求［2-8］.这种确定性的分析方法在某些情况下不能为驾驶人提供足够的行车安全保障.

针对以上不足，本文将可靠性理论用于行车视距分析，以隧道这种特殊的道路环境为切入点，在进一步考虑曲线半径、隧道侧向净宽及净高等条件下，通过分别建立平、竖曲线段的行车视距功能函数，以失效概率作为评价指标，深入研究各因素对隧道行车视距的影响.

1 可靠性功能函数

由于隧道内通常采用单向交通形式，因此本文主要考虑停车视距.根据可靠性基本理论，隧道内停车视距的功能函数可描述为

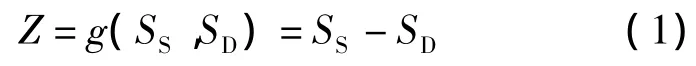
式中，Z为功能函数;SS为隧道内提供的停车视距(类似于结构中的抗力);SD为隧道内驾驶人实际需求的停车视距值(类似于结构中的荷载效应).

停车视距由驾驶人反应距离和制动距离2部分组成［9］，即

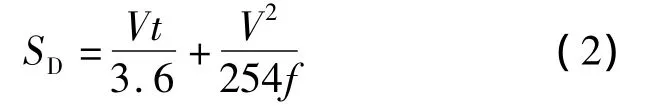
式中，V为车辆运行速度;t为驾驶人反应时间;f为路面与轮胎间的纵向摩擦系数.

将式(2)代入式(1)，则隧道内停车视距功能函数为

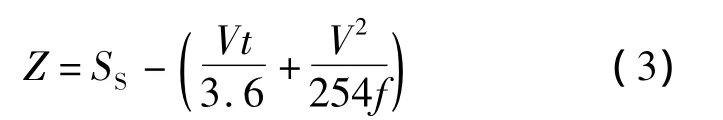
1.1 隧道内平曲线段的停车视距功能函数

图1为典型的隧道横断面图，图中Lj为路肩宽度，J为隧道内检修道宽度，Lr为隧道内人行道宽度，W为行车道宽度.

横净距、曲线半径与视距之间的关系为［1］

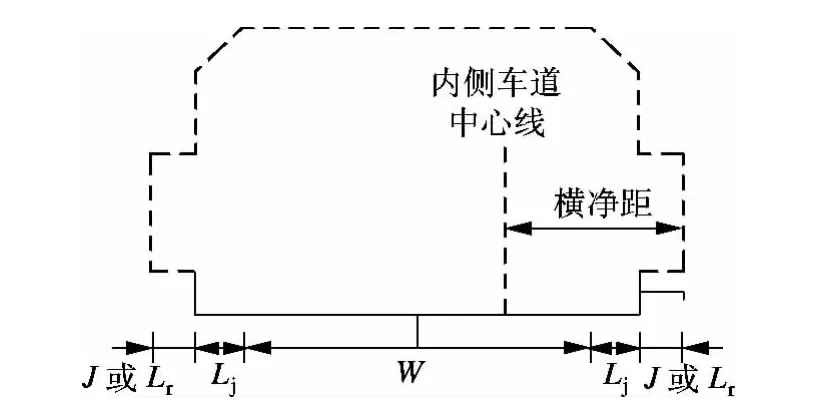
图1 公路隧道横净距

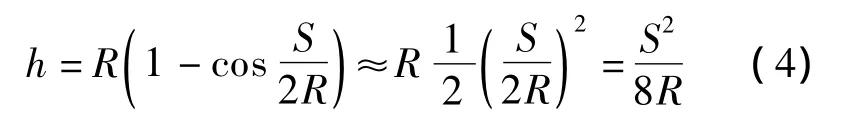
式中，h为最大横净距，即隧道内的最大侧向净宽;R为曲线半径;S为视距.

因此，平曲线段行车视距功能函数为

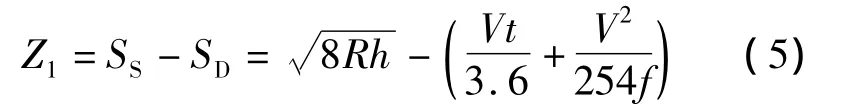
1.2 隧道内竖曲线段的停车视距功能函数

1.2.1 凸形竖曲线

凸形竖曲线的停车视距受目高、物高及竖曲线半径的影响，隧道内提供的停车视距可表示为

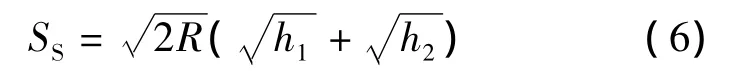
式中，L为凸形竖曲线长度;h1为驾驶人视线高，即目高;h2为障碍物高，即物高.

因此，凸形竖曲线上行车视距功能函数为

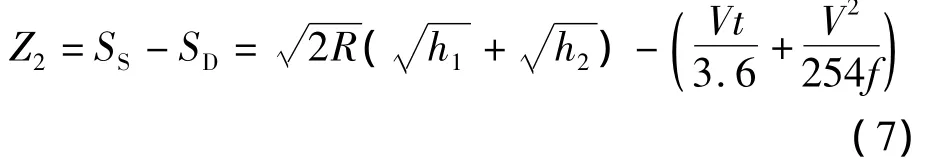
1.2.2 凹形竖曲线

在停车视距方面，与地面道路不同的是隧道内行车视距还受隧道顶部影响，如图2所示.隧道所能提供的停车视距可表示为

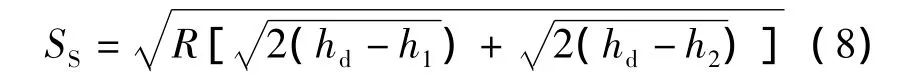
式中，hd为隧道设计净高.

因此，凹形竖曲线上行车视距功能函数为

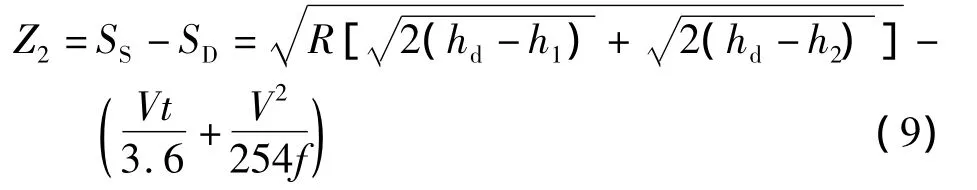
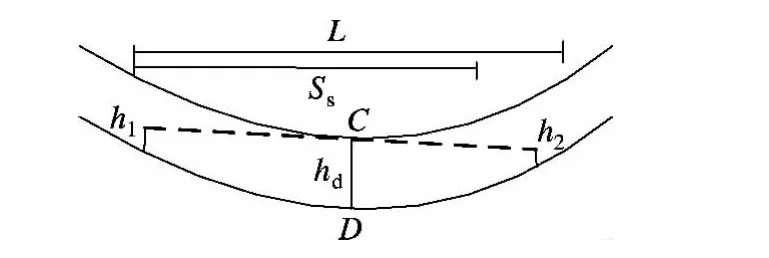
图2 公路隧道凹形竖曲线停车视距

2 可靠度求解

本文利用一次二阶矩法反复迭代求解可靠度指标，最终得到隧道内行车视距失效概率.具体求解步骤如下:

①将随机变量的分布函数转化为正态分布，则第 i个变量正态化后的均值为，方差为，其中Φ(·)，φ(·)分别为标准正态分布函数和概率密度函数，Fxi(·)，fxi(·)分别为非正态变量xi的函数和概率密度函数.

3 可靠度分析

3.1 随机变量分析

在分析隧道内行车视距功能函数时，将平、竖曲线半径、侧向净宽等道路几何参数视为确定性随机变量，而将车辆运行速度、路面摩擦系数、驾驶反应时间等作为随机变量.在计算可靠度时，随机变量的参数分布基于已有研究成果进行分析.

3.1.1 运行速度随机变量分析

运行速度是驾驶人的实际行车速度，是道路交通流实际运行情况的真实反映.研究表明:中短隧道对车辆运行速度影响不大［10］;当道路设计速度小于100 km/h时，车辆运行速度通常高于设计速度，而设计速度大于100 km/h时，运行速度一般小于设计速度［11］.且在描述道路车辆运行速度分布时大多采用正态分布模型［12］.文献［13］通过平曲线半径R预测道路的平均运行速度V50及其标准差D，其模型分别为

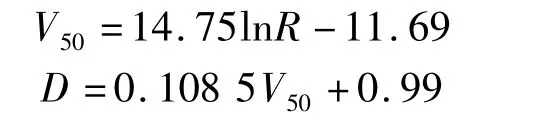
3.1.2 驾驶人目高及物高随机变量分析

目高和物高是道路线形设计中的重要设计参数.研究表明在物高接近于车尾灯高度时，车辆事故率较低，因此物高更倾向于车尾灯高度［14］.此外，据统计显示，50%的驾驶人目高超过1 149 mm，而车尾灯高度大多为 726 mm［15］.因此，可靠度分析时假设驾驶人目高、物高均服从正态分布，其均值和标准差分别为1 149 mm，55 mm和726 mm，70 mm.

3.1.3 路面摩擦系数

路面摩擦系数是反映路面抗滑能力的重要技术指标，其大小与路面本身的材料特性、冰雪天气作用、轮胎特性及汽车的行驶速度有关.现有研究大多认为路面摩擦系数服从正态分布，且采用正态分布来拟合路面摩擦系数通常具有较好的效果［16-17］.因此，可靠度分析时本文假设路面摩擦因数服从正态分布，均值和标准差分别为0.45 和0.07［18］.

3.1.4 驾驶人反应时间

反应时间是驾驶人从发现前方障碍物起到驾驶人采取制动措施并真正开始起作用时所需要的时间.调查显示，90%以上的驾驶人反应时间要小于现行设计值(2.5 s)，Davis等［19］认为反应时间近似服从对数正态分布.所以本文在可靠度分析时，假设驾驶人的反应时间服从对数正态分布，即采用Lerner［20］的研究成果，均值为 1.5 s，标准差为 0.4 s.

3.2 影响因素的敏感性分析研究

3.2.1 平曲线段停车视距的影响因素分析

本文通过改变曲线半径、路面摩擦系数、运行速度和最大横净距等参数值，分析这些因素对隧道平曲线上行车视距的影响，其中最大横净距的改变采取改变行车道的宽度实现，分别为3.0，3.25，3.5，3.75 m.表1列出了在计算过程中变量的取值的情况.计算结果如图3～图6所示.

表1 用于平曲线路段停车视距影响因素分析的参数设置

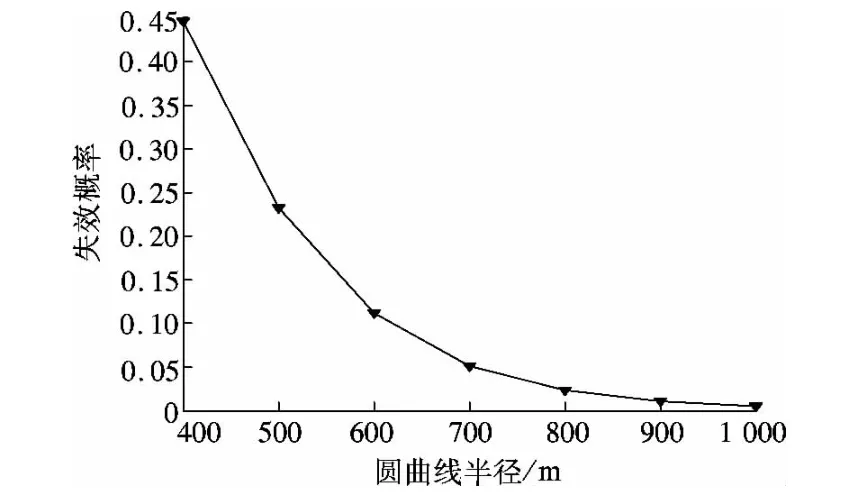
图3 圆曲线半径与失效概率的关系

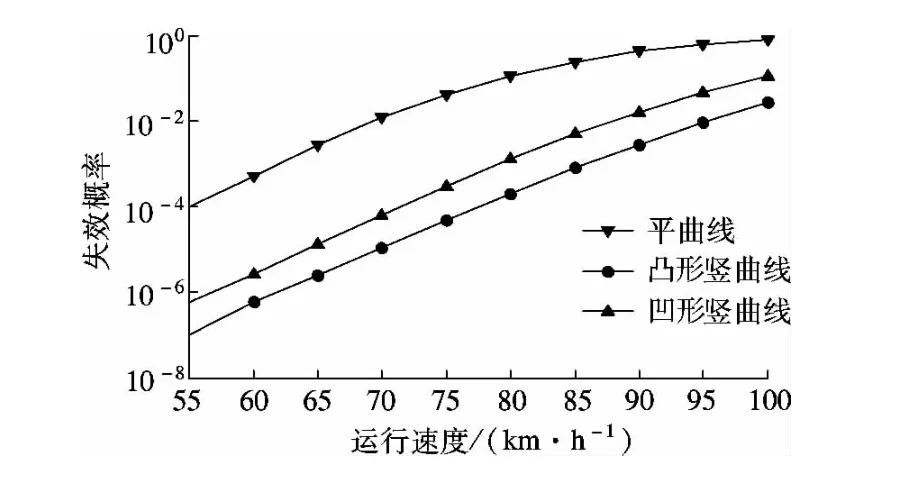
图4 运行速度与失效概率的关系

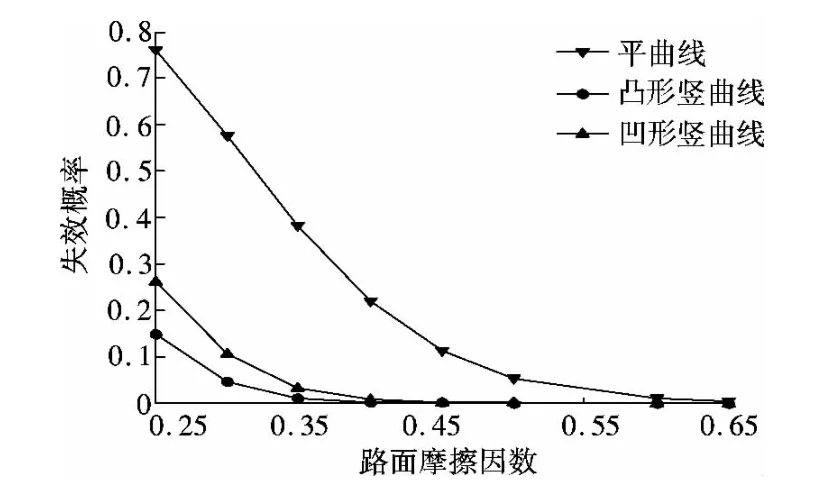
图5 路面摩擦系数与失效概率的关系

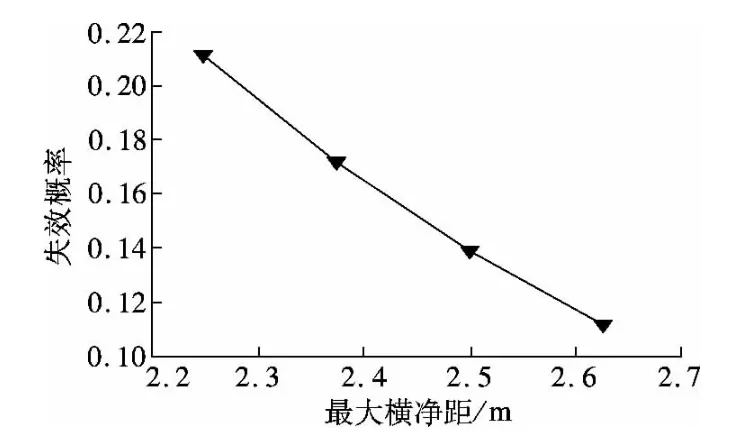
图6 最大横净距与失效概率的关系

图3和图4表明，通常情况下隧道平曲线半径和运行速度对隧道平曲线行车视距的影响较小.图5表明，当路面摩擦系数较低(小于0.40)时，平曲线上行车视距的失效概率较高.但随着路面摩擦系数的不断增大，平曲线上行车视距的可靠度越来越高.图6表明，横净距是影响隧道平曲线上行车视距的重要因素，当横净距取值较小时，行车视距的失效概率较高.

3.2.2 凸形竖曲线段停车视距的影响因素分析

在研究凸形竖曲线上行车视距时，主要考虑运行速度、路面摩擦系数及竖曲线半径对其的影响，结果分别如图4、图5和图7所示.在分析不同变量对行车视距的影响时，各个参数的设置如表2所示.

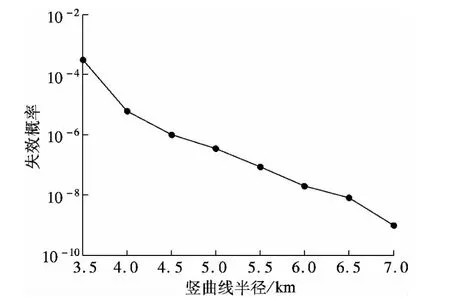
图7 凸形竖曲线半径与失效概率的关系

表2 用于凸形竖曲线路段停车视距影响因素分析的参数设置

由图4可看出，运行速度是影响隧道凸形竖曲线上行车视距的重要因素，其失效概率随着运行速度的增大而增大.图5和图7表明，行车视距的失效概率随着路面摩擦系数或曲线半径的增大而减小.

3.2.3 凹形竖曲线段停车视距的影响因素分析

对凹形竖曲线上行车视距的影响分析，以运行速度、路面摩擦系数、竖曲线半径及设计净高作为研究对象.各个参数的设置如表3所示，结果分别如图4、图5、图8和图9所示.

图4表明运行速度对凹形竖曲线上行车视距影响较小;图5表明当路面摩擦系数较低时(小于0.30)，凹形竖曲线上行车视距的失效概率较高.图8表明凹形竖曲线半径较低时(小于2 km)，竖曲线上行车视距的失效概率较高，但随着曲线半径的不断增大，竖曲线上行车视距的可靠度越来越高.图9表明当设计净高大于4.5 m时，增大设计净高对凹形竖曲线上行车视距的影响较小.

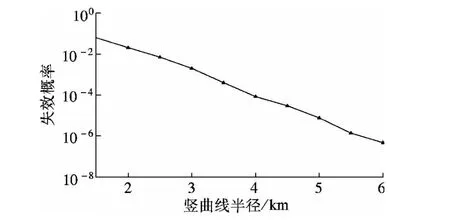
图8 凹形竖曲线半径与失效概率的关系

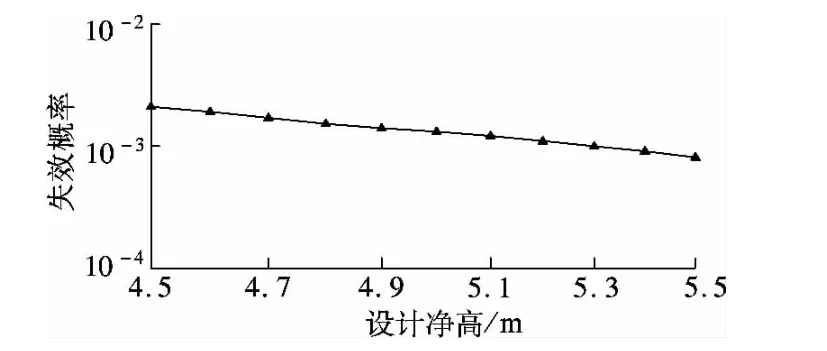
图9 设计净高与失效概率的关系

表3 用于凹形竖曲线路段停车视距影响因素分析的参数设置

4 结语

本文将可靠度理论应用于隧道的平、纵曲线段上的行车视距分析中，研究了运行速度、曲线半径、路面摩擦系数、横净距和设计净高等变量对隧道内行车视距的影响.结果表明:隧道内行车视距失效概率随着曲线半径、路面摩擦系数、设计净高、横净距的增大而减小，随着运行速度的增加而增大;设计净高、侧墙亦影响隧道内的行车视距.

由于本文中运行速度、反应时间、目高等随机变量的分布是基于现有的研究成果，因此以后可对参数的随机分布进行深入研究.另外，考虑三维空间线形作用下的隧道行车视距也是今后研究的重点.

References)

［1］韩熠，王跟民.关于公路隧道视距曲线半径的探讨［C］//全国城市公路学会第十七届学术年会论文集.绍兴，2008:28-31.Han Yi，Wang Genmin.Discussion about the curve radius of sight distance on road tunnel［C］//The 17th National City Highway Institute Annual Conference Proceedings.Shaoxing，2008:28-31.(in Chinese)

［2］Felipe E L.Reliability-based design for highway horizontal curves［D］.Vancouver，Canada:British Columbia University，1996.

［3］Faghri A，Demetsky M J.Reliability and risk assessment in the prediction of hazards at rail-highway grade crossings［J］.Transportation Research Record，1988，1160:45-51.

［4］Easa S M.Reliability-based design of sight distance at railroad grade crossings［J］.Transportation Research Part A:Policy and Practice，1994，28(1):1-15.

［5］Khoury J E，Hobeika A G.Assessing the risk in the design of passing sight distances［J］.Journal of Transportation Engineering，2007，133(6):370-377.

［6］朱兴琳，方守恩.公路路线设计可靠性分析［J］.公路交通科技，2009，26(10):135-138.Zhu Xinglin，Fang Shouen.Analysis on reliability of highway alignment design［J］.Journal of Highway and Transportation Research and Development，2009，26(10):135-138.(in Chinese)

［7］朱兴琳.基于可靠度理论的公路路线设计［J］.长安大学学报:自然科学版，2010，30(4):46-50.Zhu Xinglin.Highway geometric design based on reliability theory ［J］.Journal of Chang’an University:Natural Science Edition，2010，30(4):46-50.(in Chinese)

［8］Zheng Z R.Application of reliability theory to highway geometric design［D］.Vancouver，Canada:The University of British Columbia，1997.

［9］杨少伟.道路勘测设计［M］.北京:人民交通出版社，2007:121-122.

［10］方靖，汪双杰，祝站东，等.高速公路隧道路段大型车运行速度模型［J］.交通运输工程学报，2010，10(3):90-93.Fang Jing，Wang Shuangjie，Zhu Zhandong，et al.Operating speed models for trucks at expressway tunnel sections［J］.Journal of Traffic and Transportation Engineering，2010，10(3):90-93.(in Chinese)

［11］Mclean J R.Speeds on curves:side friction factor considerations［R］.Victoria，Canada:Australian Road Research Board，1978.

［12］Fambro D B，Koppa R J，Picha D L，et al.Driver braking performance in stopping sight distance situations［J］.Transportation Research Record，2000，1701:9-16.

［13］Andjus V，Maletin M.Speeds of cars on horizontal curves［J］.Transportation Research Record，1998，1612:42-47.

［14］Fambro D B，Fitzpatrick K，Koppa R J.New stopping sight distance model for use in highway geometric design ［J］.Transportation Research Record，2000，1701:1-8.

［15］Fitzpatrick K，Fambro D B，Stoddard A M.Safety effects of limited stopping sight distance on crest vertical curves ［J］.Transportation Research Record，2000，1701:17-24.

［16］Fambro D B，Fitzpatrick K，Koppa R J.Determination of stopping sight distances［J］.Transportation Research Record，1997，1467:9-11.

［17］Lamm R，Psarianos B，Mailaender T.Highway design and traffic safety engineering handbook［M］.New York:Mcgraw-Hill，1999:28-32.

［18］You K，Sun L，Gu W.Reliability-based risk analysis of roadway horizontal curves［J］.Journal of Transportation Engineering，2012，138(8):1071-1081.

［19］Davis G A，Sanderson K，Davuluri S.Development and testing of a vehicle/pedestrian collision model for neighborhood traffic control［R］.Twin Cities，MN，USA:University of Minnesota，2002.

［20］Lerner N.Age and driver perception-reaction time for sight distance design requirements［C］//Institute of Transportation Engineers 65th Annual Meeting.Washington，DC，USA，1995:624-628.

［21］重庆交通科研设计院.JTG D70—2004公路隧道设计规范［S］.北京:人民交通出版社，2004.