紧致麦克风阵列压缩采样与DOA估计方法

王青云 赵 力 梁瑞宇 王 侠 孟 桥

(1东南大学信息科学与工程学院，南京 210096)(2南京工程学院通信工程学院，南京 211167)

紧致麦克风阵列压缩采样与DOA估计方法

王青云1，2赵 力1梁瑞宇1，2王 侠1孟 桥1

(1东南大学信息科学与工程学院，南京 210096)
(2南京工程学院通信工程学院，南京 211167)

摘 要:针对紧致麦克风阵采样信号大量冗余的问题，提出了一种ΣΔAD压缩采样方法.该方法将软硬件相结合，在ΣΔAD转换器内部进行压缩采样.压缩采样中采用自适应过程，去除信号中的冗余分量，并将压缩后的信号进行稀疏编码.仿真结果表明，使用该方法对紧致麦克风阵接收信号进行压缩编码时，通过选取合适的稀疏化阈值，可使源数据的压缩比达到10% ～30%.压缩采样后的信号可以用于DOA估计等应用.针对八元紧致麦克风圆阵和DSP实时系统的DOA估计实验结果表明:这种DOA估计方法在阵元间距低至2 cm时仍能正常工作;当阵列尺寸减小时，相比经典MUSIC算法和PHAT-GCC算法，该方法定位精度更高，噪声鲁棒性更强.

关键词:紧致麦克风阵列;压缩采样;DOA估计

香农信息论认为信号采样必须满足Nyquist 定理.但是，近年来的压缩感知理论认为，只要信号满足稀疏性，或者数据有冗余，就可以用低于Nyquist频率的采样频率进行采样［1-2］.当前对于压缩感知的研究大多集中于对高速采样后的数据进行压缩，需要处理大量的原始数据，计算量大，浪费了大量的系统资源［3］.Candes等［4］指出压缩感知的核心问题应该是在采样的过程中对信号进行压缩.因此，需要寻求一种可以用软硬件联合实现的压缩采样方法，在信号进行模拟至数字转换的同时进行压缩，摒弃繁琐的“采样→数字化→压缩”过程［5］.

在压缩采样与量化测量的理论框架［6］下，研究者们提出了一些针对声信号［7］、图像信号［8］和通信信号等压缩采样的软硬件方法.利用压缩传感对麦克风阵列接收信号进行解相关，减小冗余，提高声源定位分辨率，是麦克风阵列信号处理中的新方向［9-10］.Malioutov 等［11］提出了一种基于过完备稀疏基的压缩传感声源定位方法，采用不同角度的导向矢量组成过完备基，利用观测信号和稀疏基组成的代价函数对声源位置进行估计;该方法可以估计空间中多个声源的位置，而且适用于宽带信号.但是过完备基组成的矩阵规模庞大，占用大量的存储空间，导致较大的计算负荷，并不适用于实时系统.在文献［12］所提出的Min-Max最优化框架基础之上，本文提出了一种紧致麦克风阵列ΣΔAD压缩采样和DOA估计方法.该方法将传统ΣΔ调制器和AD转换器相结合，在过采样ΣΔAD转换器内部进行压缩，去除信号中的冗余分量，将压缩后的信号进行稀疏编码，用于信号压缩和DOA估计等应用.

1 压缩采样ΣΔAD转换器

图1(a)为传统阵列信号采样框图.阵列的输入模拟信号X(n)经过AD转换单元，被量化编码为数字信号D(n)，后续的数据处理算法对D(n)进行处理.AD转换单元对阵列信号各通道分别采样，当各通道信号高度相关时，采样得到的D(n)数据存在大量冗余.图1(b)为ΣΔAD压缩采样框图.前端的模拟部分增加了可硬件实现的压缩变换单元，对输入模拟信号X(n)进行压缩变换，消除各通道信号之间的相关性.变换后的阵列信号进入过采样ΣΔAD变换器，过采样状态变量W(n)利用自适应算法控制压缩变换单元的参数，以达到最佳效果，并通过稀疏化单元得到最终的稀疏信号.

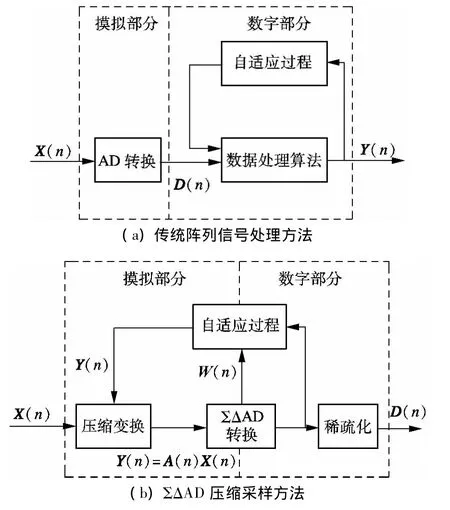
图1 阵列信号采样框图

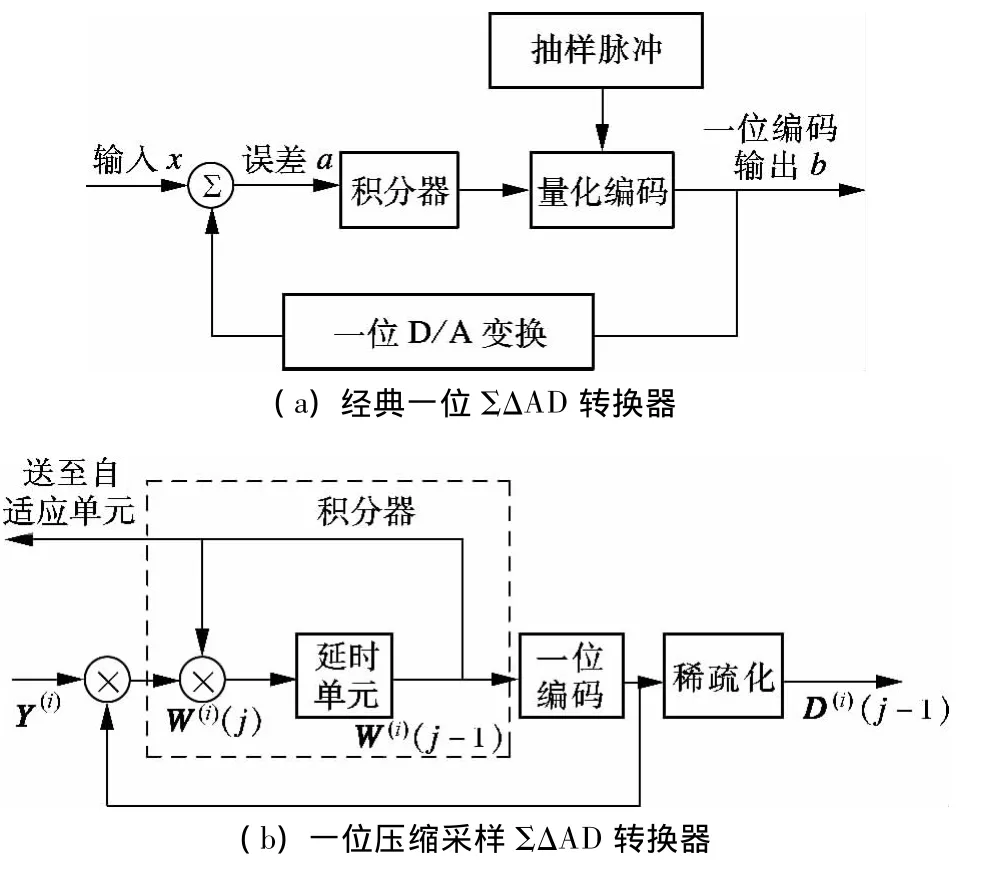
图2 经典与压缩采样ΣΔAD转换器

图1(b)中的ΣΔAD变换器源于如图2(a)所示的经典一位ΣΔAD转换器［13］.图2(b)为一位压缩采样ΣΔAD转换器框图.通道i中经压缩变换后的信号Y(i)不仅经过ΣΔ调制输出量化的一位编码，而且在编码之前输出中间状态信号W(i)，该状态信号送至自适应过程单元，调整压缩变换参数.压缩变换域的编码信号经过稀疏化过程，抛弃变换域中能量较小的点，保留系数值较大的样点输出.

2 压缩采样自适应过程

图1(b)中的压缩变换单元可以用变换矩阵A表示.经过压缩变换后的阵列信号为

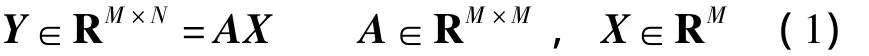
式中，M为传感器阵列的阵元个数，也称为通道数;N为样点数.为了使得对压缩采样信号的重建过程始终是稳定可靠的，将变换矩阵A选为对角元为1的确定性下三角阵，该结构有利于硬件实现.

在图1(b)所示的ΣΔAD压缩采样方案中，根据AD转换器输出的状态变量W，调整变换矩阵A的系数，使得输出信号Y=AX的能量最小［15］.将自适应过程的目标函数定义为

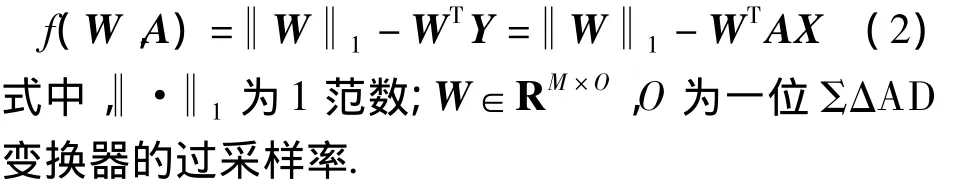
在输出信号Y=AX的能量最小条件下，根据梯度下降算法，可以推导得到

⑥切换到n+1时刻，返回步骤②，直至信号处理完毕.

3 仿真与实验

3.1 语音压缩编码实验

实验测试了麦克风阵接收混叠语音信号的压缩编码性能，采用扬声器播放来自TIMIT语音库的语音文件进行测试，随机抽取30组语音片段进行.通道1和通道2分别输入2路不相关的纯净语音信号，通道3和通道4输入前2路语音信号的线性混合信号，4个通道信号已同步.利用本文方法所得的一组压缩编码输出信号波形图见图3.从图中可以看出，通道3和通道4采样信号的幅值和能量大幅减小，配合后续的稀疏化单元，可以大幅缩小数据量和存储量.图4为对应的压缩编码重建信号波形与重建语谱图.从图中可以看出，通道3和通道4重建波形恢复了原始输入信号波形，4个通道的语谱图声纹清晰，试听语音质量良好.

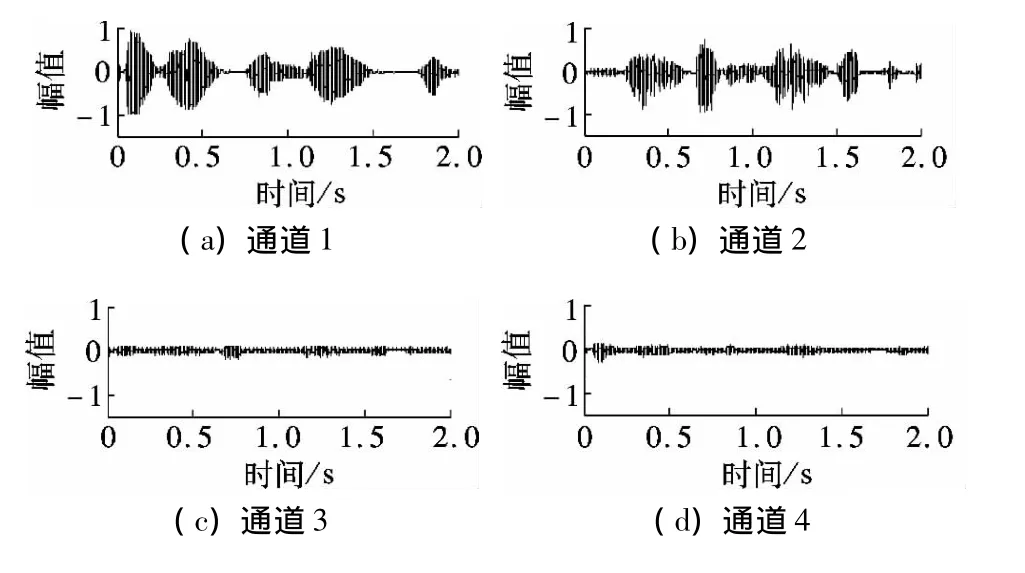
图3 压缩编码输出信号波形

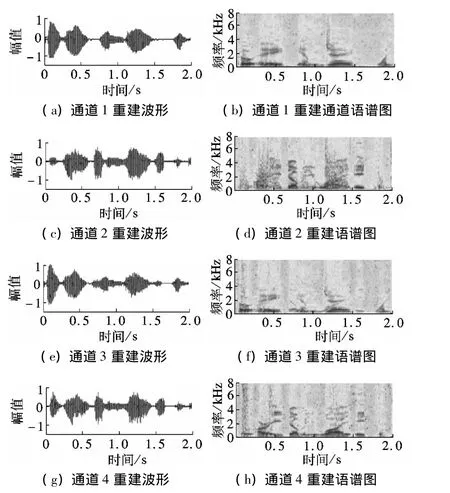
图4 压缩编码重建信号波形与语谱图

3.2 稀疏性与失调率实验

本实验测试图2(b)中稀疏化单元阈值与重建信号失调率的关系.其中，压缩比定义为压缩后和压缩前的数据容量比值，失调率M定义为压缩前和压缩后信号差异的2范数，即

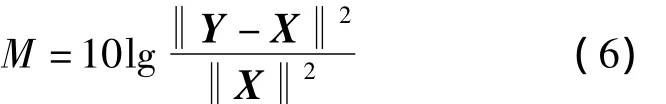
实验结果见图5.由图5(a)可以看出，选取合适的稀疏化阈值，源数据的压缩比可以达10% ～30%.O=32，64，128时均取得了较好的压缩比，且O=128时的图线下降速度最快，压缩比最低，但是优势并不明显.由图5(b)可以看出，重建数据与源数据的失调率随稀疏化阈值的增加而上升.阈值上升，数据的压缩比下降，但是失调率也随之增大.实际系统中应根据精度要求和压缩比要求选取合适的阈值.

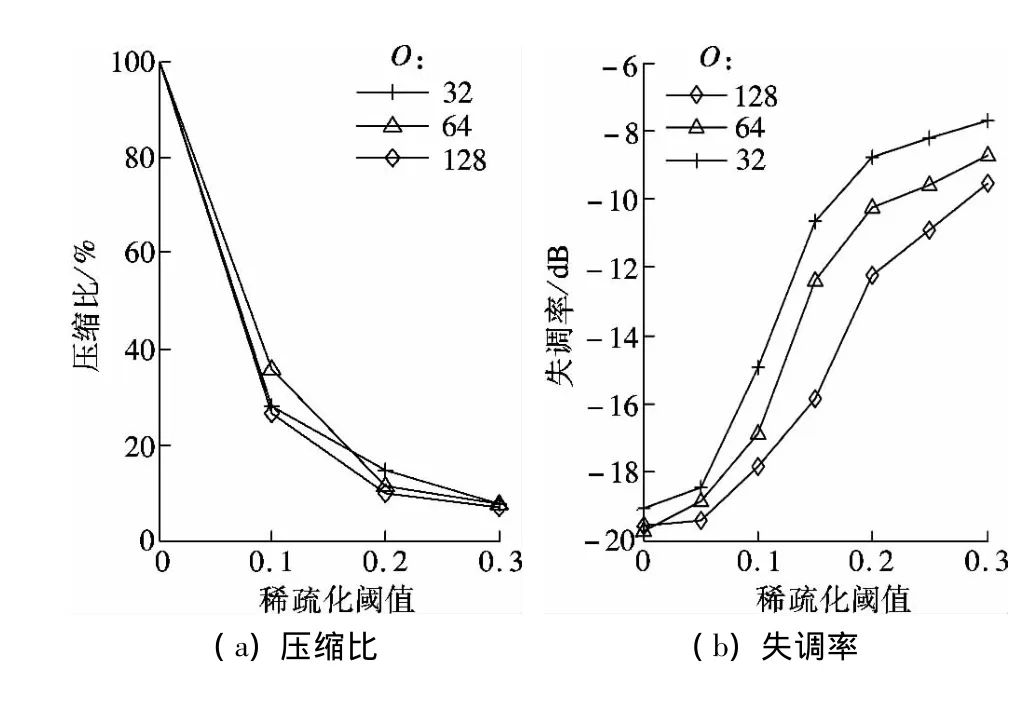
图5 稀疏化阈值与重建信号性能

重建信号信噪比采用分帧方式计算，即

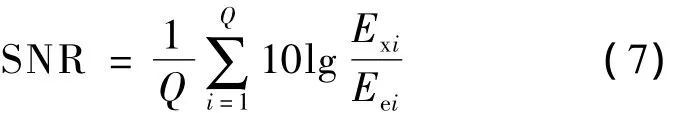
式中，Q为总帧数;Exi为第i帧信号能量;Eei为第i帧误差能量.实验得到的压缩比与重建信号信噪比关系见表1.

表1 压缩比与重建信噪比

压缩比的减小意味着数据量的减小.但是，随着压缩比的减小，重建信号信噪比相应降低，重建后的信号质量变差.当压缩比达到20%时，重构信噪比接近于0，说明噪声与有用信号能量接近.因此，在实际应用中，应根据信号质量与数据量的具体要求，调整并选取合适的压缩比.

3.3 紧致麦克风阵DOA估计实验

满足式(2)～(5)得到的变换矩阵A可以用于阵列信号DOA参数提取.DOA估计是麦克风阵声源定位经典问题［16］，由于估计误差随麦克风阵孔隙的减小而增大，经典算法在阵元孔隙小于厘米级时常常失效.利用压缩采样方法，各阵元差模信号被提取并放大，共模部分被去除，DOA估计精度提高.

对于DOA问题而言，获取阵元与参考信号的延迟，即可得到阵列流型矩阵，并进一步得到波达方向.采用本文方法后，麦克风阵列输出信号Y=AX，根据式(2)～(5)提出的自适应过程，在得到的输出信号Y中，y(1)=x(1)为参考信号，y(2)，y(3)，…，y(M)为各阵元相对参考信号变换后的压缩信号.压缩信号保持了与参考信号的相对时延关系，利用各通道之间的时延即可完成DOA估计.

实验采用八元麦克风圆阵，半径 r=2，5，10 cm，声源扬声器距离圆阵圆心1 m，测试范围为0°～360°，每30°为1个测试位置点，共12个测试位置.每个位置取值为10段语音信号测试平均值，信号采样率为16 kHz.图6为实验系统框图.

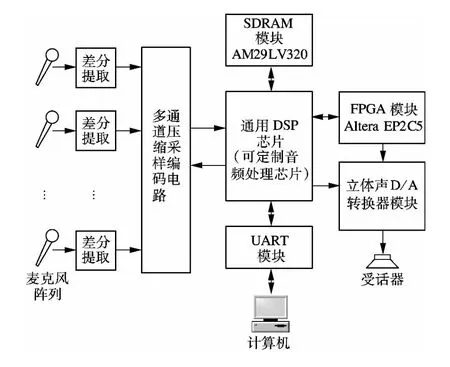
图6 八元麦克风圆阵DOA估计系统框图

表2为无噪和信噪比20 dB时的DOA估计结果.为节约篇幅，表中所示角度偏差值为12个测试点的偏差平均值.由表可知，在阵列尺寸较小时，相比经典的MUSIC算法和PHAT-GCC算法，本文方法显示出更优异的性能.前两者只能用于常规尺寸麦克风阵，当阵列尺寸小至厘米级(圆阵半径减小至2 cm或以下)时，这些经典算法无法获得正确的估计值;而本文方法由于有效提取了各阵元接收信号的差异部分，仍然能够获得较好的估计效果.

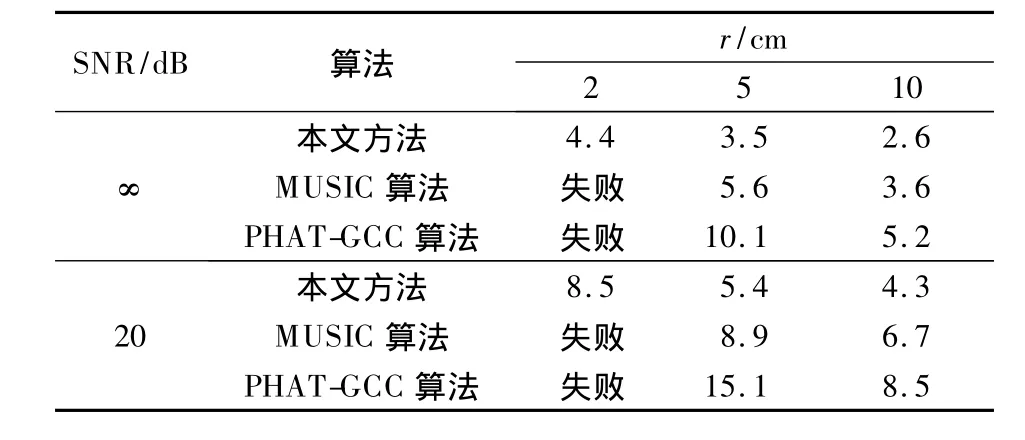
表2 不同信噪比情况下的平均估计偏差值 (°)

在上述八元麦克风阵条件下，不同误差范围要求时本文算法的DOA估计成功率见表3.由表可知，本文方法在声源到达角为0°～90°时取得了较为均匀的成功率.鉴于八元麦克风阵的对称结构，可以推测出0°～360°范围内的DOA估计性能是类似的.含噪信号的DOA估计成功率比无噪信号低.误差范围为±5%时的成功率低于±10%时的成功率.无论声源距离麦克风阵中心位置为1 m还是2 m，当误差范围为±10%时，实验在不同声源角度处均取得了不低于87%的成功率.

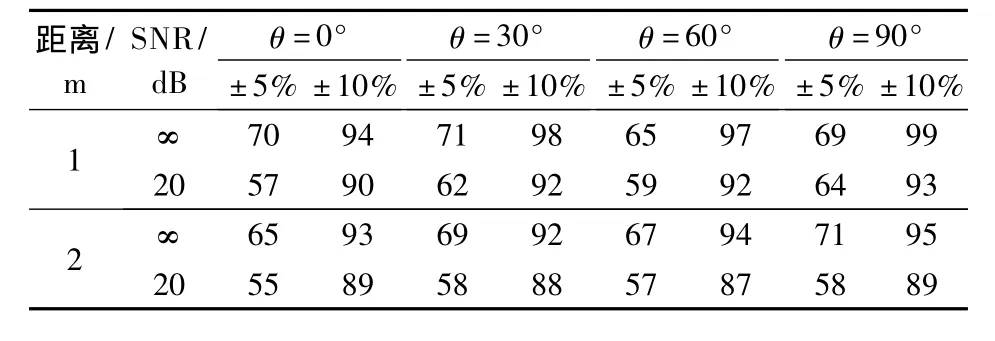
表3 DOA估计成功率 %

4 结语

本文提出了一种紧致麦克风阵列ΣΔ压缩采样和DOA估计方法，通过将模数混合电路和软硬件相结合，实现了采样过程中的数据压缩.本文方法可以从根本上消除阵列中的冗余信息，输出压缩编码信号，并可用于DOA估计等声源定位应用.该方法实时性强，可以从本质上消除数据采样中的冗余问题，节约存储空间和计算工作量.更进一步，通过选取不同的自适应目标函数和收敛过程，可将本文方法拓展至各类信号处理应用中.

［1］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［2］Akcakaya M，Tarokh V.Shannon-theoretic limits on noisy compressive sampling［J］.IEEE Transaction on Information Theory，2010，56(1):492-504.

［3］Peng Maoling，Chen Shanxiong，Yu Guanglin.Sparse recovery and compressive sampling based on FFT and DWT［C］//Proceedings of the International Confer-ence on Information Engineering and Applications.London:Springer，2012:619-624.

［4］Candes E，Wakin M B.An introduction to compressive sampling ［J］.IEEE Signal Processing Magazine，2008，25(2):21-30.

［5］Candes E，Romberg J.Sparsity and incoherence in compressive sampling［J］.Inverse Problems，2007，23(3):969-985.

［6］Zymnis A，Boyd S，Candes E.Compressed sensing with quantized measurements［J］.IEEE Signal Processing Letters，2010，17(2):149-152.

［7］Luo Chenchi.Compressive sampling with a successive approximation ADC architecture［C］//Proceedings of2011IEEEInternationalConferenceonAcoustics，Speech and Signal Processing(ICASSP). Prague，Czech Republic，2011:3920-3923.

［8］Wu A B，Burnaby B C，Sarunic M V，et al.Quantitative evaluation of transform domains for compressive sampling-based recovery of sparsely sampled volumetric OCT images［J］.IEEE Transactions on Biomedical Engineering，2012，60(2):470-478.

［9］Ayllon D，Gil-Pita R，Rosa-Zurera M.Optimum microphone array for monaural and binaural in-the-canal hearing aids［C］//Proceedings of2011IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing(CAMSAP).San Juan，Puerto Rico，2011:177-180.

［10］Li X，Ma X，Yan S，et al.Single snapshot DOA estimation by compressive sampling［J］.Applied Acoustics，2013，74(7):926-930.

［11］Malioutov D，Cetin M，Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays［J］.IEEE Transactions on Signal Processing，2005，53(8):3010-3022.

［12］Amit Gore，Ahantanu Chakrabartty.A min-max optimization framework for designing ΣΔ learners:theory and hardware［J］.IEEE Transactions on Circuits and SystemsⅠ:Regular Papers，2010，57(3):604-617.

［13］de la Rosa J M.Sigma-delta modulators:tutorial overview，design guide，and state-of-the-art survey［J］.IEEE Transactions on Circuits and SystemsⅠ:Regular Papers，2011，58(1):1-21.

［14］Donoho D L，Huo X.Uncertainty principles and ideal atomic decompositions［J］.IEEE Transactions on Information Theory，2001，47(7):2845-2862.

［15］Amin Fazel， Shantanu Chakrabartty. Sigma-delta learning for super-resolution source separation on highdensity microphone arrays［C］//Proceedings of2010IEEE Proceedings of Circuits and Systems(ISCAS).Paris，France，2010:797-800.

［16］Benesty Jacob，Chen Jingdong，Huang Yiteng.Microphone array signal processing［M］.Berlin，German:Springer，2008:187-199.

Compressive sampling and DOA estimation method for miniature microphone array

Wang Qingyun1，2Zhao Li1Liang Ruiyu1，2Wang Xia1Meng Qiao1
(1School of Information Science and Engineering，Southeast University，Nangjing 210096，China)
(2School of Communication Engineering，Nanjing Institute of Technology，Nanjing 211167，China)

Abstract:Aiming at the problem of the redundancy of the sampled data in a compressive microphone array，a new ΣΔAD(analog-digital)compressive sampling method is proposed.Combined with software and hardware，the input signals are compressively sampled within the ΣΔAD converter.With the help of adaptive estimation procedure in sampling，the redundancy of the input signal is removed and the sparse output signal is encoded.The simulation results demonstrate that the compression rate is 10%to 30%when the proper sparseness threshold is set for the miniature microphone array during the signal coding process by this method.The compressively sampled signal can be used in the applications such as direction of arrival(DOA)estimation.The experimental results for an eight-component miniature microphone array and a real-time digital signal processing system demonstrate that when the aperture of the microphone array is low to 2 cm，the direction of the arrival is estimated successfully by this DOA estimation method.When the aperture of the array decreases，compared with the traditional multiple signal classification(MUSIC)algorithm and the phase transform generalized cross-correlation(PHAT-GCC)algorithm，the proposed DOA estimation method exhibits higher positioning accuracy and noise robustness.

Key words:miniature microphone array;compressive sampling;direction of arrival(DOA)estimation

中图分类号:TP391.42

A

1001－0505(2014)04-0687-05

doi:10.3969/j.issn.1001 －0505.2014.04.001

收稿日期:2013-12-23.

王青云(1972—)，女，博士，副教授;赵力(联系人)，男，博士，教授，博士生导师，zhaoli@seu.edu.cn.

基金项目:国家自然科学基金资助项目(61301219，61375028)、中国博士后基金资助项目(2012M520973)、江苏省自然科学基金资助项目(BK20130241)、南京工程学院科研基金资助项目(ZKJ201202).

王青云，赵力，梁瑞宇，等.紧致麦克风阵列压缩采样与DOA估计方法［J］.东南大学学报:自然科学版，2014，44(4):687-691.［doi:10.3969/j.issn.1001 －0505.2014.04.001］