EBPSK编码调制的二次监视雷达测速性能分析
2014-09-17卢从慧李玉书吴乐南
卢从慧 李玉书 吴乐南
(1东南大学信息科学与工程学院,南京 210096)(2北京跟踪与通信技术研究所,北京 100094)
EBPSK编码调制的二次监视雷达测速性能分析
卢从慧1李玉书2吴乐南1
(1东南大学信息科学与工程学院,南京 210096)
(2北京跟踪与通信技术研究所,北京 100094)
摘 要:为了解决二次监视雷达(SSR)接收到目标应答信号时受到异步干扰的问题,在SSR对目标的应答信号的脉冲宽度内,引入扩展二元相移键控(EBPSK)对载波进行相位编码调制.理论分析了SSR系统中速度与频偏的关系,通过研究EBPSK相位调制脉冲的波形特点,提出了将EBPSK相位编码脉冲信号作为SSR系统应答信号的方案,从而有效利用异步干扰提升双基站SSR系统的目标测速精度.理论分析与仿真实验结果表明,在目标测速精度方面,EBPSK相位编码的双基站SSR系统明显优于EBPSK相位编码以及纯正弦调制脉冲的单基站SSR系统.因此,验证了EBPSK相位编码脉冲信号在双基站雷达系统中的有效性和可行性.
关键词:二次监视雷达;扩展二元相移键控;测速;频偏
二次监视雷达(secondary surveillance radar,SSR)通过询问和接收空中机载或箭载应答机的反馈信息,来发现和识别空中目标.但在多部SSR系统目标轨迹跟踪的过程中,如果目标处于多部SSR系统测量的交接区域,多部SSR间的协调失误会导致同类SSR询问机同时向目标发送询问指令,从而引起应答机的重复应答,使得SSR接收机受到相邻SSR系统的应答干扰[1].此协调失误还会破坏未编码SSR信号的目标测量时序,从而引起异步干扰[2].本文以双基站SSR系统为例,采用扩展二元相移键控(EBPSK)[3-4]对SSR脉冲信号进行相位编码,从而有效利用该异步干扰来提升每个SSR在交接区域速度测量的精度.
本文首先对未编码和EBPSK相位编码的SSR测速系统进行了理论分析,然后给出了在应答回波混叠时双基站SSR测速性能的理论结果.仿真结果表明,基于EBPSK脉冲调制的双基站SSR在测速性能方面优于基于纯正弦和EBPSK脉冲调制的单基站SSR系统.
1 系统模型建立
假定存在A,B两部同类SSR询问机以相同的脉冲重复频率分别向目标应答机发送询问信号,SSR基站A,B分别对空中一目标进行速度跟踪,系统模型如图1所示.其中SSR基站的询问脉冲重复频率(pulse repetition frequency,PRF)为fr;被基站检测的空中目标机载应答机发送信号的信息位脉宽为Tp;脉冲传输速度假定为光速c;目标和基站接收机之间的初始距离为R0;目标以径向速度vr匀速运动,对应目标运行速度为vr/cosα,其中α表示目标和基站接收机的径向连线与地面的夹角.

图1 SSR基站与被测目标之间运动关系模型图
1.1 SSR的应答信号
被测目标应答机接收到SSR地面站发射的询问信号后,由询问信号的内容自动回应一串脉冲,此串脉冲即为应答信号,在时间域上为间断、重复的脉冲序列.其若干个信号周期的波形见图2.

图2 SSR应答信号格式(单位:μs)
每个信号周期内应答码由16位信息码组成,除特殊位置识别信号 SPI距F2的脉冲间隔为(4.35±0.1)μs外,其余任意一个信息位距离 F1的间隔为(1.45n±0.1)μs,其中n=1 ~14,n∈N+,每个信息码脉冲宽度均为(0.45 ±0.1)μs.F1 和 F2脉冲前沿间隔为(20.3 ±0.1)μs,称为框架脉冲[5],是SSR系统应答回波的标志脉冲,恒为1.本文将此应答信号F1与F2框架脉冲中的各信息位以随机生成的“1”或“0”信息作为应答编码.
由于2部SSR接力进行目标轨迹连续测量与跟踪的过程中,目标交接区域会因相邻的同类SSR询问机协调失误而都在发送询问指令,触发应答机重复应答.应答机的重复应答会导致应答信号在一些时延段出现应答脉冲的混叠,发生异步干扰即越界自动交接问题[6-7].下面分析该异步干扰对SSR测速性能的影响.
1.2 EBPSK 调制
EBPSK调制波形的表达式为

式中,s0(t)和s1(t)分别表示发送“0”码元和“1”码元时[0,T]区间EBPSK的调制输出波形;T为码元周期;fc为载波频率;θ=0~π为“跳变角”;τ为跳变所持续的载频周期数;T=N/fc=NTc,N为码元周期与载波周期之比;K为每个EBPSK码元中跳变部分所占的载波周期数[8].这里统一令θ=π,K=1.
为便于对不同SSR基站进行区分,将SSR的信息码元使用伪随机M序列编码[9].受应答机信息码脉冲宽度限制,脉内信号M序列的编码长度只能为3位,则基站A对应的M序列为[1 0 1],基站B对应的M序列为[0 1 1].当该M序列编码值为“0”时,输出调制波形为s0(t),当M序列编码值为“1”时,输出调制波形为s1(t),则可得EBPSK调制M序列编码的信号表达式为

式中,M∈{0,1}是M序列的调制码元.
在目标应答机的发送信号调制中,由于脉冲持续时间仅0.45 μs,则单个脉冲内有13.5 个载波周期,为了使每个脉冲内有尽可能多的码元个数,取N=3.那么EBPSK调制M序列编码只能在0.3 μs内实现,则在剩余的0.15 μs脉宽内,填入4.5个载波周期的正弦信号,其信息幅度与该脉冲的幅度一致,以充分利用带宽,如图3所示.

图3 应答回波信号单个脉宽内EBPSK调制波形
2 SSR测速性能理论分析
2.1 速度与频偏的关系
当SSR的基站处于接收状态时,应答回波信号输出3路信号,分别为和通道、方位差通道、仰角差通道信号[10],其中和通道信号中包含目标的距离、速度参数.假定被测目标应答机发射的应答回波为单频信号,即

式中,U1为信号幅度;φ1为信号瞬时相位;ω0为信号角频率;φ0为信号初始相位.由SSR接收端收到的应答回波信号可得,被测目标相对于SSR基站的径向速度为

式中,fd为多普勒频率;fsend0为被测目标应答机发射频率.由式(4)可知,测速实际就是测多普勒频偏fd.
2.2 3种SSR信号模型测速性能的分析
首先,通过对单个脉宽内的频谱分析,比较频偏估计^fd的精度.由式(1)、(2)可得,SSR目标应答机发送的一个脉宽内信号的表达式为


[(n-1)(Tp+T0),(n-1)(Tp+T0)+Tp],n∈N+;sM(t)表示SSR信号为EBPSK调制的M序列;SE0(t)表示应答机输出为EBPSK调制的“0”码元信号s0(t).则应答机被基站A与基站B所发的EBPSK调制“0”码元信号触发后的应答信号表达式分别为


而式(5)中Simp(t)为s1(t)中跳变部分,Sno_imp(t)为s1(t)中未跳变部分,那么令SSR基站A所触发的目标应答机发送的EBPSK调制信号中与Simp(t)对应的部分为SimpA(t),与Sno_imp(t)对应的部分为Sno_impA(t).因此,SimpA(t)和Sno_impA(t)的表达式分别为

式中,h表示每个脉宽内载波相位的第h次跳变,对应于基站A的M序列编码[1 0 1],h取值为1或2.
同理,令SSR基站B所触发的目标应答机发送的EBPSK调制信号中与Simp(t)对应的部分为SimpB(t),与Sno_imp(t)对应的部分为Sno_impB(t).由于基站B的M序列编码为[0 1 1],其各脉宽内第h次跳变的位置会不同于基站A,但h取值仍为1或2.于是有

因此,将式(6)~(8)分别代入式(5)可得单基站SSR纯正弦波波形,以及SSR基站A、基站B的EBPSK调制波形.它们对应目标应答机发送信号波形的频谱幅值表达式为

式中,Fsin(f)表示单基站SSR纯正弦调制时波形频谱;FM(f)表示单基站SSR EBPSK调制时波形频谱;Fimp(f)对应s1(t)中跳变部分的频谱,Fno_imp(f)为s1(t)中未跳变部分的频谱,分别与式(5)中Simp(t)和Sno_imp(t)相对应;FE0(f)表示EBPSK调制中发“0”码元s0(t)时信号频谱幅值.由式(5)、(6)可得

SSR基站A和B在M=1时的频谱幅值表达式分别为

因此可得,SSR基站接收端信号的频谱幅值表达式为

式中,Fr(f)为接收信号的频谱幅值;ρ(f)为信道的衰减因子;Fs(f-fd)为目标应答机的发送信号频谱;N(f)为信道中的噪声频谱.
定义Fgoal=Fr(fc+fd)为基站接收信号频谱在fc+fd处的幅值,令信道噪声能量为E,则Fgoal/E决定着系统SSR信号的频偏估计^fd的精度.在相同的信道条件下,上述3种不同信号模型频偏估计^fd的精度与Fgoal值是正相关的,即

由式(13)可知,系统SSR信号的频偏估计值^fd与fd差值绝对值越小,接收信号频谱在fc+fd处的幅值Fgoal则越小,反之亦然.
由式(9)可得,不同调制目标应答机发送信号频谱在载频fc处的幅值为

令本文3种SSR信号模型信号单个脉宽内的频谱在fc+fd处的幅值分别为FAgoal(或FBgoal),F(A+B)goal,Fsin_goal,根据式(12)可得

可得3种模型的信号单个脉宽内的频谱在fc+fd处幅值的关系式为

即3种SSR信号模型的测速性能比较结果为:采用双基站SSR(基站A与基站B均工作时)EBPSK调制时最优,单基站SSR纯正弦调制时其次,单基站SSR EBPSK调制时最差.
可见,当双基站SSR测速时,由于2个同类SSR之间异步干扰的存在使得F(A+B)goal值增加.因此,将目标应答机对两基站询问机响应的异步干扰加以利用,可有效提升测速性能.
3 SSR测速性能仿真
本节通过多个仿真实验对上文3种SSR信号模型测速性能的理论分析进行验证.系统主要参数为:fc=30 MHz;10倍采样率;fr=300 Hz;信号周期数为30;vr=275.23 m/s时,被测目标应答机的发射频率fsend0=1.09 GHz,则对应多普勒频移fd=1.0 kHz;基站接收到的应答信号格式满足SSR的信号调制格式.
3.1 只有单个SSR基站
令SSR单个基站的M序列编码为[1 0 1],SSR各脉宽内分别为纯正弦波调制与EBPSK调制,在相同信噪比条件下SSR的频偏估计性能如图4所示.

图4 滤波前单基站在不同调制时的频偏估计性能比较
基站接收到的应答信号若经过窄带滤波处理,将会有效提升系统频偏估计性能,尤其在信噪比较低时,窄带滤波器对系统频偏估计性能的提升更为明显,如图5所示.

图5 单基站滤波前后频偏估计性能比较
比较图4和图5的频偏估计性能曲线可知,当系统中只有单个SSR基站时,在相同的信噪比下,采用脉内EBPSK调制的测速性能不如脉内为纯正弦波调制时,这是因为相比纯正弦调制时的幅值,EBPSK调制时信号的频谱幅值有所下降,与2.2节的理论分析结果一致.
3.2 有两个处于不同位置的同类SSR基站
令基站A采用M序列编码[1 0 1],基站B采用M序列编码[0 1 1],且基站B应答信号相对于基站A应答信号存在时延.
如图6所示,在相同信噪比条件下比较上述3种情况下的频偏估计性能可知,双基站明显优于单基站.虽然单基站脉内纯正弦调制优于单基站脉内EBPSK调制,但仍不如双基站脉内EBPSK调制,验证了第2节的理论分析是正确的.
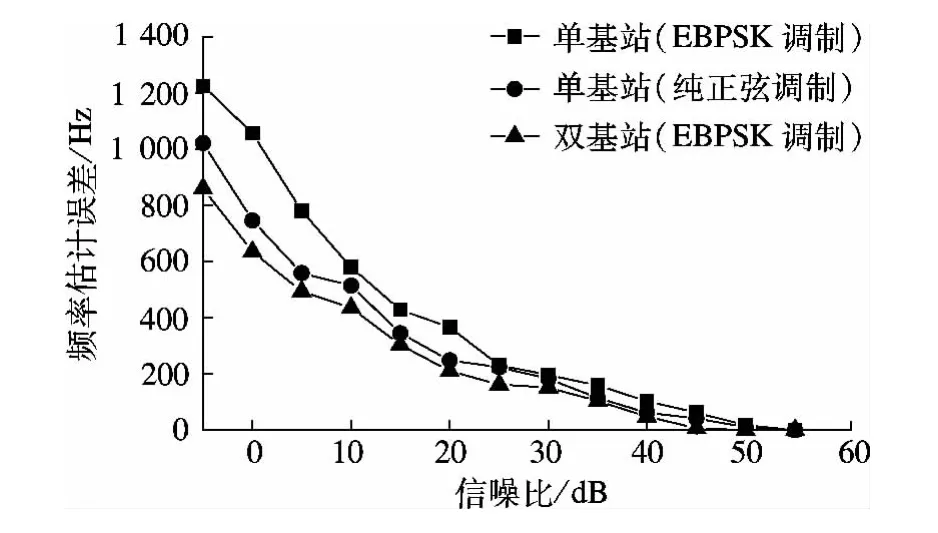
图6 滤波后单、双基站的频偏估计性能比较
4 结语
在保证SSR测量精度的前提下,为了提高SSR目标越界交接的自动化水平,本文分析了受到异步干扰时的SSR测速性能.谱线跟踪分析和应答回波的频偏估计仿真表明:尽管相同信噪比条件下,在单基站雷达系统中,EBPSK调制脉冲信号的测速精度不如纯正弦调制方式,但EBPSK脉冲调制的双基站SSR雷达的测速精度和应答信号载波能量的增加,明显优于单基站纯正弦脉冲.因而本文提出的EBPSK脉冲编码调制可以有效地解决SSR的异步干扰问题.
[1]Xu J,Yu J,Peng Y N,et al.Radon-Fourier transform for radar target detection(Ⅱ):blind speed sidelobe suppression[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(4):2473-2489.
[2]Cui G,DeMaio A,Piezzo M.Performance prediction of the incoherent radar detector for correlated generalized Swerling-chi fluctuating targets[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):356-368.
[3]Wu L N,Feng M,Qi C H,et al.Recent patents on ultra narrow band modulations[J].Recent Patents on Signal Processing,2011,1(1):36-47.
[4]陈鹏,吴乐南.压缩感知在多载波EBPSK雷达中的应用[J].东南大学学报:自然科学版,2014,44(1):23-27.
Chen Peng,Wu Lenan.Compressive sensing for multicarrier EBPSK radar[J].Journal of Southeast University:Natural Science Edition,2014,44(1):23-27.(in Chinese)
[5]Svabenik P,Zeman D,Balada R,et al.Separation of secondary surveillance radar signals[C]//34th International Conference on Telecommunications and Signal Processing.Budapest,Hungary,2011:487-490.
[6]张尉.二次雷达原理[M].北京:国防工业出版社,2007:31-33.
[7]Koga T.Autonomous continuous target tracking for multi-sensor systems and its application for radar network[C]//10th International Symposium on Autonomous Decentralized Systems.Kobe,Japan,2011:157-163.
[8]张士凯,吴乐南.EBPSK调制信号功率谱分析[J].电波科学学报,2008,23(3):496-500.
Zhang Shikai,Wu Lenan.PSD analysis of EBPSK modulated signals[J].Chinese Journal of Radio Science,2008,23(3):496-500.(in Chinese)
[9]逯科,王元利.M序列波形编码性能研究及计算机仿真[J].现代防御技术,2008,36(6):120-123.
Lu Ke,Wang Yuanli.Study and simulation on the performance of coding wave shape by M-sequence[J].Modern Defence Technology,2008,36(6):120-123.(in Chinese)
[10]Millet N,Klein M.Passive radar air surveillance:last results with multi-receiver systems[C]//Proceedings of International Radar Symposium.Leipzig,Germany,2011:281-285.
Performance analysis of SSR speed measurement based on EBPSK modulation
Lu Conghui1Li Yushu2Wu Lenan1
(1School of Information Science and Engineering,Southeast University,Nanjing 210096,China)
(2Beijing Institute of Tracking and Telecommunication Technology,Beijing 100094,China)
Key words:secondary surveillance radar(SSR);extended binary phase shift keying(EBPSK);speed measurement;frequency deviation
中图分类号:TN958.96
A
1001-0505(2014)04-0692-05
doi:10.3969/j.issn.1001 -0505.2014.04.002
收稿日期:2013-12-30.
卢从慧(1988—),女,博士生;吴乐南(联系人),男,博士,教授,博士生导师,wuln@seu.edu.cn.
基金项目:国家自然科学基金资助项目(61271204)、“十二五”国家科技支撑计划资助项目(2012BAH15B00).
卢从慧,李玉书,吴乐南.EBPSK编码调制的二次监视雷达测速性能分析[J].东南大学学报:自然科学版,2014,44(4):692-696.[doi:10.3969/j.issn.1001 -0505.2014.04.002]Abstract:To solve the problem that the target response signal of secondary surveillance radar(SSR)is interfered by the asynchronous interference,the extended binary phase shift keying(EBPSK)is introduced for carrier phase coded modulation within the radar pulse width.The relationship between the target speed and the deviation of frequency in the SSR system is analyzed theoretically.By studying the waveform characteristics of the EBPSK-based phase-coded pulse signal,a scheme taking EBPSK-based phase-coded pulse signal as the response signal in the SSR system is proposed,where the asynchronous interference of the SSR system is used effectively to improve the precision of speed measurement.The theoretical and simulation results show that the speed measurement precision of bistatic SSR signals with EBPSK modulation is better than that of single SSR signal with sine and EBPSK modulation.Therefore,the efficiency and feasibility of the EBPSK-based phase-coded pulse signal is verified in the bistatic SSR system.
