对一道弹簧问题的思考与解析

马富山

(兰州市第六十一中学 甘肃 兰州 730060)

从近几年高考的弹簧类问题设置的特点来看，以轻质弹簧为载体，设置复杂的物理情境，涉及的力学规律较多，多考查学生的综合分析能力.下面的这一道弹簧问题对培养学生综合分析物理问题的能力很有帮助，而在弹簧类问题中我们却又很容易忽略.笔者根据自己的理解和经验对这一道习题进行分析和解答.

图1

【例题】如图1所示，一根轻弹簧竖直直立在水平面上，下端固定.在弹簧正上方有一个物块从高处自由下落到弹簧上端，将弹簧压缩.当弹簧被压缩了x0时，物块的速度减小到零.从物块和弹簧接触开始到物块速度减小到零的过程中，物块的加速度大小a随下降位移大小x变化的图像，可能是下图中的

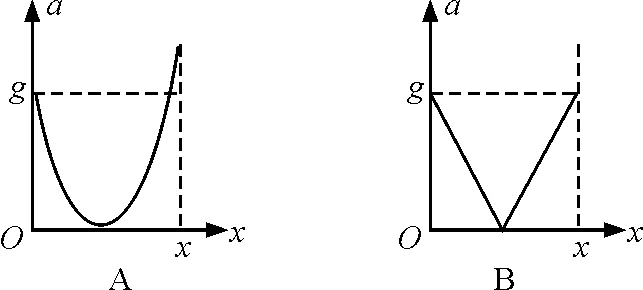
分析：(1)本题考查了牛顿第二定律和匀变速直线运动的图像，属于牛顿运动定律综合专题．

(2)对学生来说，这道题目比较难，加上对弹簧类问题的自然畏惧，学生常找不到头绪，思维混乱，无从下手.对学生而言，本题障碍点主要出现在以下几个方面：

1)物块和弹簧接触后的受力变化、运动状态分别是怎样的？

2)速度的最大值和最小值分别对应着哪个状态？

3)物体在最低点的加速度与重力加速度之间的大小关系是什么？

(3)本题的难点在于物体在最低点的加速度与重力加速度之间的大小关系.

针对学生思维的障碍点将难题分解，回归基本模型，逐一分析，则能帮助学生突破难点，迅速找到思路.更能培养学生化繁为简，迁移、发散的能力.

图2

基本模型：如图2所示，一轻质弹簧竖直放在水平地面上，小球A由弹簧正上方某高度自由落下，与弹簧接触后，开始压缩弹簧，设此过程中弹簧始终服从胡克定律，那么在小球压缩弹簧的过程中，以下说法中正确的是

A.小球加速度方向始终向上

B.小球加速度方向始终向下

C.小球加速度方向先向下后向上

D.小球加速度方向先向上后向下

正确答案：C.

例题解答：我们知道物块所受的力为弹力和重力，而弹力与形变量成正比，所以加速度与位移之间也应该是线性关系，加速度与位移关系的图像为直线.

(1)物块接触弹簧后

在开始阶段，物块的重力大于弹簧的弹力，合力向下，加速度向下，根据牛顿第二定律得

mg-κx=ma

得到

由上式可知a与x是线性关系，当x增大时，a减小.

(2)当弹力等于重力时，物块所受合力为零，加速度a=0，此时速度最大.

(3)当弹力大于重力后，物块的合力向上，加速度向上，根据牛顿第二定律得

κx-mg=ma

得到

由上式可知a与x是线性关系，当x增大时，a增大.

难点处理方法1：简谐运动对称性

若物块从弹簧原长，即自由端处释放，加速度大小为g，方向向下，根据简谐运动对称性，可知最低点时所受的合力也是mg，方向向上，所以弹力为2mg，加速度为g.若物块从弹簧原长位置上端的更高处由静止释放，或者从弹簧原长处有初速度释放，由对称性知新的最低点将更低，弹簧压缩量也更大，弹簧向上的弹力更大，产生的弹力必定大于2mg，而向下的重力不变，则向上的合外力更大，向上的加速度大小大于g.故选项D正确.

难点处理方法2：动能定理

根据动能定理第一个过程(从物块与弹簧接触到物块速度最大)合力做的功小于第二个过程(从物块速度最大到物块的速度减为零)合力做的功，而合力-位移图像中图线下的面积表示合力做的功，由选项中图像分析可得选项D正确.

难点处理方法3：能量守恒

设下落到最低点时，下落的高度为h，由题意，当弹簧压缩的长度为x0时动能为零，由能量守恒得

(1)

此时受到的力为

G=mgF弹力=κx0

(2)

由公式(1)、(2)得

因为h>x0(因为一开始自由下落，所以下落高度肯定大于弹簧压缩长度),所以弹力大于2mg，此时加速度

方向竖直向上.

点评：本题根据牛顿第二定律得到a关于x的解析式，根据解析式选择图像是常用方法.难点在于确定小球在最低点的加速度大小大于重力加速度，本题分别利用简谐运动的对称性、动能定理和能量守恒3种方法对难点进行了处理．这样可以使学生从多个角度来理解.通过本题的训练，学生已经掌握弹簧类问题的受力特点和运动特点，能抓住特殊位置，寻找解题的突破口.

总结：在平时的物理教学中，学生常常反映解题难.其中重要的原因之一就是学生对题目的物理过程不理解.所以，在平时的教学过程中教师一定要注意培养学生分析、总结的能力.千变万化的物理习题都是根据一定的物理模型，结合某些物理关系，给出一定的条件后，再求相应物理量的.而解题的过程，就是将题目所给的复杂过程中隐含的物理模型还原,确定满足的物理规律，列出物理关系再求所求量的过程.