基于T-S模糊神经网络组合模型的CPI预测

荀新新， 张德生， 王 雁， 杜方欣

(西安理工大学 理学院， 陕西 西安 710054)

0 引言

在实际问题的预测中，由于建模和出发点不同，对同一问题通常采用不同的预测方法.不同的预测方法提供不同的有用信息，其预测精度往往也是不同的.如果我们简单的将一些误差较大的预测方法舍弃，将会失去一些有用的信息，这种做法会浪费掉一些信息，应予以避免.一种更科学的方法是，将不同的预测方法进行适当的组合，形成所谓的组合预测方法，这种方法综合利用了各种方法所提供的信息，提高了预测精度，比单个预测方法更系统、更全面，有效地减少单个模型预测过程中一些环境因素的影响.

早在1969年，Bates和Granger[1]证明了2种或2种以上无偏的单项预测可以组合出优于每个单项预测的结果.郭宁、向凤红[2](2008)建立灰色理论与神经网络的串行组合模型，并使用该组合模型对股票价格进行了预测.数值实验表明，组合模型预测结果比单一模型有所改进.王聚杰、王建州[3](2011)建立基于小波去噪的组合了含有季节项的累积式自回归-移动平均(SARIMA)和BP神经网络的预测模型对短期电力负荷进行预测，并且使用方差-协方差法确定组合权重，取得了较高的预测精度.陈娟、赵耀江[4](2012)以适合预测具有波动性序列的马尔可夫预测模型对灰色模型进行修正，建立灰色马尔可夫组合模型，对我国煤矿事故发生率进行了预测，其预测精度有很大提高.

文章将在两种单模型的基础上，建立T-S模糊神经网络组合模型，并对我国的CPI进行预测.

1单模型CPI预测

由于我国从2001年开始计算CPI定基价格指数，首轮基期为2000年，所以采用我国2000年1月到2013年2月的CPI与PPI月度数据，共158个数据构建模型，并利用2013年3月到7月的数据进行CPI预测效果检验.建模前先对数据进行平稳化处理，CPI和PPI一阶差分后为平稳时间序列，分别记为：DCPI、DPPI，用DCPI和DPPI序列建立模型进行预测.采用循环预测的方法，即每次预测一期，把新的预测值添加到原样本中继续预测下一期，如此循环往复，直到预测到第5期.

1.1 VAR模型

VAR(向量自回归)模型[5]把系统中每个内生变量作为系统中所有的内生变量滞后值的函数来构造模型，从而将单变量的自回归模型推广到由多元时间序列变量组成的向量自回归模型.

VAR(p)模型的一般形式为：

yt=Φ1yt-1+…+Φpyt-p+Hxt+εt

t=1,2,…,n

(1)

其中，yt是内生变量的k维列向量，xt是外生变量的d维列向量，p是滞后阶数，T是样本的个数.k×k维矩阵Φ1,…,Φp和k×d维矩阵H是待估的系数矩阵，而εt是k维误差列向量，它们之间允许相关，但是这些误差变量不允许自相关，与等式右边的变量也不相关.

对DCPI和DPPI建模，由LR、HQ和SC准则确定出VAR模型的最佳滞后阶数为1.使用Eviews 5.0软件，建立模型如下：

DPPI=0.694 087 378 2×DPPI(-1)+0.223 608 354 1×DCPI(-1)-0.012 701 272 91

DCPI=0.166 994 804 6×DPPI(-1)+0.018 139 217 98×DCPI(-1)-0.017 482 598 77

1.2 加外生变量的半参数自回归模型

1986年，Engle，Gronger等在研究气候条件对电力需求影响这一实际问题时提出了半参数自回归模型[6]，而CPI和PPI之间又有一定的传导关系，所以可以把PPI作为外生变量建立加外生变量的半参数自回归模型.

半参数自回归模型的表达式：

(2)

对于DCPI、DPPI序列，利用AIC和BIC准则定阶得：p1=3，p2=2；由CV准则，窗宽hn=0.01×n-1/5；核函数取多维高斯正态核K(u)=(2π)-1/2exp(-u2/2).通过运行MATLAB程序，得到模型的最小二乘核估计，故可建立模型：

Yt=0.072 9Xt+0.116 4Xt-1+0.115 1Xt-2+

g(Yt-1,Yt-2,Yt-3)+et

(3)

其中,et是白噪声，Yt=DCPI,Xt=DPPI.

2 T-S模糊神经网络组合模型

模糊神经网络[7-9]是一种集模糊数学逻辑推理的强大结构性知识表达能力与神经网络的强大自学习能力于一体的新技术，它是模糊逻辑推理与神经网络有机结合的产物.

2.1 模糊数学简介

模糊数学[10-12]是用来描述、研究和处理事物所具有的模糊特征的数学，“模糊”是指它的研究对象，而“数学”指它的研究方法.

模糊数学中最基本的概念是隶属度和模糊隶属度函数.其中，隶属度是指元素u属于模糊子集F的隶属程度，用μF(u)表示，它是一个在[0,1]之间的数.μF(u)=1，表示u完全属于F；μF(u)=0，表示u完全不属于F；0<μF(u)<1，表示u部分属于F.模糊隶属度函数是用于定量计算元素隶属度的函数，一般包括三角函数、梯形函数和正态函数等.

2.2 T-S模糊模型

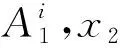
该模糊推理表示输出向量为输入向量的线性组合，其中，输入的部分是模糊的，输出的部分是确定的.

i=1,2,…,n

(4)

其中，∧表示模糊算子.根据模糊计算结果计算模糊模型的输出值Y.

(5)

2.3 T-S模糊神经网络模型

T-S模糊神经网络[14,15]有五层分别是：

输入层：每个节点与输入向量xj(j=1,2,…,k)连接，节点数与输入向量的维数相同，将输入向量传送到下一层.

模糊化层：根据模糊规则计算各输入变量xj的隶属度，本文模糊隶属函数选用高斯正态函数：

j=1,2,…,k;i=1,2,…,n

(6)

模糊规则计算层：每个节点代表一条模糊规则，采用模糊连乘公式(4)计算得到适用度{ωi}.

输出层：采用公式(5)计算模糊模型的输出值Y.

2.4 学习算法

(1)误差计算

(7)

其中，ydi是网络期望输出；yi是网络实际输出；E为期望输出和实际输出的误差.

(2)系数修正

(8)

(9)

(3)参数修正

隶属度函数参数调整可采用BP网络误差反转算法，以提高学习速度和增加算法的可靠性.

(10)

(11)

2.5 实证分析

采用VAR模型和加外生变量半参数自回归模型的CPI预测值和拟合值，就可以建立T-S模糊神经网络组合模型.以2000年1月到2013年2月的CPI月度数据作为训练数据，以2013年3月至7月的CPI作为测试数据.T-S模糊神经网络模型的输入数据为两种单模型的拟合值，输出数据为CPI真实值，故模型的输入节点数为2，输出节点数为1，隐含层节点数设为4.运行MATLAB程序得到CPI的拟合值和5期预测值.

T-S模糊神经网络组合模型对CPI的拟合值和实际值比较结果如图1所示，可以看出该模型对CPI月度数据拟合效果比较准确.

图1 T-S模糊神经网络组合模型的拟合图

2.6 模型预测比较

为了更好的研究所建立模型的优劣，对VAR模型、加外生变量的半参数自回归模型和T-S模糊神经网络组合模型的预测结果进行比较，结果见表1，并计算出其平均绝对误差(MAE)、均方误差(MSE) 和平均相对误差(MPE)，结果见表2.

表1 三种模型的预测值和相对误差

表2 三种模型预测精度的比较

实证结果表明，与前两种单模型相比，T-S模糊神经网络组合模型的预测精度得到了一定的提高，是一种比较有效的预测方法 .

3 结束语

文章在两种单模型的基础上，运用T-S模糊神经网络组合模型对我国CPI月度数据进行了预测，预测精度得到了一定的提高.该模型将模糊系统良好的模糊知识表达能力与神经网络强大的自学习和自适应能力有机结合，具有非线性逼近能力强、训练速度快和算法稳定等优点，是一种行之有效的预测方法.

[1] Bates J.M,Granger C.W.J.The combination of forecast[J].Operational Research Quarterly,1969,20:450-468.

[2] 郭 宁，向凤红．基于灰色神经网络组合模型的股票价格预测研究[D]．昆明：昆明理工大学，2008．

[3] 王聚杰，王建州．基于小波去噪的组合预测模型及其在短期电力负荷预测中的应用[D]．兰州：兰州大学，2011．

[4] 陈 娟，赵耀江.我国煤矿事故统计分析及基于最佳组合模型的预测研究[D].太原：太原理工大学，2012.

[5] 高铁梅.计量经济分析方法与建模：Eviews应用及实例[M].北京：清华大学出版社，2009：230-256．

[6] 叶阿忠.非参数计量经济学[M].天津：南开大学出版社，2005:179-185.

[7] MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010:218-229.

[8] Han Min,Fan Yingnan.Extened fuzzy neural network based on T-S model and its application[J].Journal of Systems Engineering,2007,22(5):532-538.

[9] 孙月峰，闫雅飞.基于T-S模型的模糊神经网络城市需水量预测方法研究[J].安全与环境学报，2013,13(2):110-115.

[10] 陈 兴，孟卫东，严太华.基于T-S模型的模糊神经网络在股市中的应用[J].系统工程理论与实践，2001,21(2):98-103.

[11] Ajoy Kumar Palit,D.Popovic.Nonlinear combination of forecasts using Artificial neural network[J].Fuzzy Logic and Neuro-Fuzzy Approaches,2000(10):561-566.

[12] 傅荟璇，赵 红.MATLAB 神经网络应用设计[M].北京：北京机械出版社，2010:124-129.

[13] 刘婷婷，邓克涛，马昌喜.模糊神经网络非线性组合预测在铁路货运量预测中的应用[J].铁道运输与经济，2008,30(9):56-62.

[14] 韩 敏，范迎南.基于T-S模糊神经网络模型的改进和应用[J].系统工程学报，2007,22(5):532-538.

[15] Wang Shuai,Sun Yuefeng.Urban water consumption prediction based on a partial least-square model coupled with step-wise regression[J].Journal of Safety and Environment,2012,12(4):170-173.