一类带时滞的退化半线性抛物方程组解的存在性研究

陆求赐 (武夷学院人文与教师教育学院,福建 武夷山 354300)

江秋香 (闽江学院数学系,福建福州350121)

一类带时滞的退化半线性抛物方程组解的存在性研究

陆求赐 (武夷学院人文与教师教育学院,福建 武夷山 354300)

江秋香 (闽江学院数学系,福建福州350121)

考虑了一类带时滞的退化半线性抛物型方程组解的存在性问题。在一定的假设条件下,利用上下解与正则化方法证明了方程组的解是局部存在的,在一定条件下解甚至会在有限时刻产生猝灭的现象;同时也证明了初值函数满足一定条件时解是全局存在的。

退化半线性抛物方程组;时滞;初值函数;存在性;熄灭

抛物方程(组)的存在性与熄灭现象在研究稳定或不稳定的燃烧过程中都起着重要作用,同时在研究生态理论和相应的环保理论过程中也起着重要作用[1-15]。自从Kawarada的关于带奇异项的反应函数f(u)=(1-u)-1的一维热方程[3]的工作出现以来,解的存在性与熄灭问题引起了广大数学工作着的极大的关注,各种各样推广的抛物型初边值问题得到了研究。这些推广包括多维抛物型方程[1,4]、更一般的反应函数[1,5-6]、退化抛物型方程[7]以及带时滞的正则抛物型方程[1]等等。文献[8,11]研究了退化抛物方程解的存在性与熄灭现象,文献[1,9,15]研究了带有时滞的一致抛物方程的存在性与熄灭问题。下面,笔者将文献[8-9,15]中带有时滞的退化抛物方程推广为方程组,并对带有时滞的退化半线性方程组解的存在性提供充足的条件。

带有时滞的半线性抛物方程组解的存在性问题表述如下:

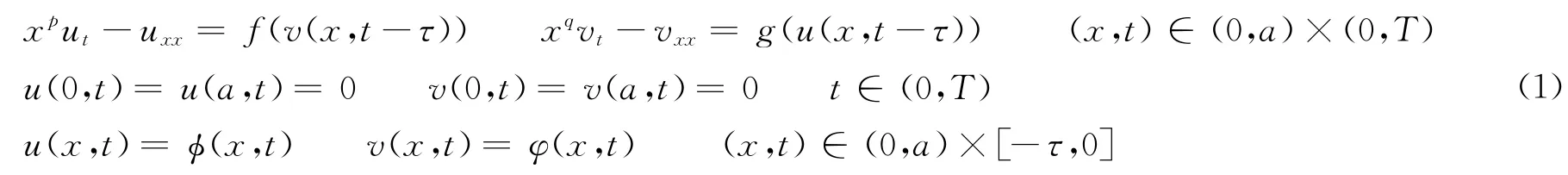
式中,p,q≠0;0＜T≤∞为正常数;τ和a分别为表示时滞与区间(0,a)的长度的正常数。

1 假设条件

对奇异反应函数f,g与初值函数φ(x,t),φ(x,t)作如下假定:

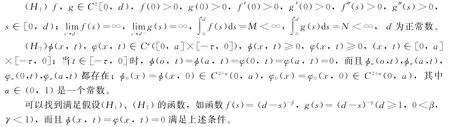
根据文献[2,9]的理论,当方程组(1)不包含时滞时,将与如下的稳定态方程组(2)正解的存在与不存在性紧密联系:

2 解的局部存在性

为了得到问题(1)的古典解,首先给出如下比较原则:

其中,ε∈(0,a),而且φ(x,t),φ(x,t):[ε,a]×[-τ,0]→R是初值问题(1)简单的一个截断。显然有,)=(h(x,t),k(x,t))与,)=(0,0)为(7)在(ε,a)×(0,t0]上的一对上下解。采用文献[1]中定理2.8.1相同的方法可以证明正则抛物问题(7)有一个C2,1解(uε,vε)。

再采用引理1相同的方法,可以证明如下的引理:

如果c(x,t),d(x,t)∈C([ε,a]×[0,T))而且在(ε,a)×(0,T)内,c(x,t)≥0,d(x,t)≥0,那么在[ε,a]×[0,T)上,h(x,t)≥0,k(x,t)≥0。

根据文献[1]的引理2.2.1与引理4,容易得到如下的单调性结果:

引理5令0＜ε1＜ε2＜a,并假定(uε1,vε1),(uε2,vε2)为(7)解,那么在(ε2,a)×(0,t0]内,有(uε1,vε1)＞(uε2,vε2),即uε1＞uε2,vε1＞vε2。设:

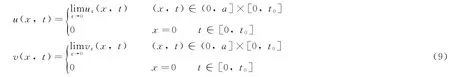
根据引理1～引理5的内容以及文献[12]的定理2.3与定理2.5的标准内容,可以得到如下关于解的存在性与熄灭结果的定理:

定理1在假设(H1)、(H2)之下,方程组(1)在(0,a)×(0,t0]内有一个古典解(u(x,t), v(x,t))。令T为使得问题(1)在(0,a)×(0,t0]内有唯一正古典解的t0的最小上界,则问题(1)在(0,a)×(0,T)内存在唯一正的古典解(u(x,t),v(x,t))。而且如果T＜∞,有:

3 全局存在性

[1]Pao C V.Nonlinear Parabolic and Elliptic Equations[M].New York:Plenum Press,1992.

[2]Pao C V.Blowing-up of solution for a nonlocal reaction-diffusion problem in combustion theory[J].Journal of Mathematical and Applications,1992,166(2):591-600.

[3]Karawada H.On solutions of initial boundary problem for ut=uxx+1/(1-u)[J].Publ RI MS Kyoto Univ,1975,15:729-736.

[4]Acker A,Walter W.The Quenching Problem for Nonlinear Partial Differential Equations[M].Berlin:Springer-Verlag,1976.

[5]Chan C Y,Ke L,Vatsala A S.Impulsive quenching for reaction diffusion equations[J].Nonlinear Analysis,1994,22(11):1323-1328.

[6]Chan C Y,Kong P C.Quenching for degenerate semilinear parabolic equations[J].Applicable Analysis,1994,52(1):17-25.

[7]Deng K.Dynamical behaviour of solutions of a semilinear heat equation with nonlocal singularity[J].SI AM J Math Anal,1995, 26(1):98-111.

[8]Ke L,Ning S.Quenching for degenerate parabolic equations[J].Nonlinear Analysis,1998,34(7):1123-1135.

[9]Pao C V.Quenching problem of a reaction-diffusion equation with time delay[J].Nonlinear Analysis,2000,41(1):133-142.

[10]Chan C Y,Liu H T.Global existence of solutions for degenerate semilinear parabolic problem[J].Nonlinear Analysis,1998, 34(4):617-628.

[11]Sheng Q,Khaliq A Q.A compound adaptive approach to degenerate nonlinear quenching problems[J].Numerical Methods for Partial Differential Equations,1999,15(1):29)47.

[12]Floater M S.Blow up at the boundary for degenerate semilinear parabolic equations[J].Archive for Rational Mechanics and Analysis,1991, 114(1):57-77.

[13]Friedman A.Partial Differential Equations of Parabolic Type[M].Inc Engle wood Cliffs:Prentice-Hall,1964.

[14]Martel Y,Souplet P.Small time boundary behavior of solutions of parabolic equations with noncompatible data[J].J Math Pure Appl,2000,79(6):603-632.

[15]陈友朋.带时滞的退化半线性抛物方程的熄灭(英文)[J].南京师大学报(自然科学版),2006:29(1):7-13.

[编辑]洪云飞

O175.26

A

1673-1409(2014)28-0009-04

2014-06-18

福建省自然科学基金资助项目(Z0511015);武夷学院校科研基金资助项目(XL1204)。

陆求赐(1975-),男,硕士,讲师,现主要从事基础数学和偏微分方程的教学与研究工作。