几个恒等式及其组合方法的证明

周 恩，霍元极

（1.海南软件职业技术学院基础部，海南琼海571400；2.河北北方学院数学系，河北张家口075000）

几个恒等式及其组合方法的证明

周 恩1，霍元极2

（1.海南软件职业技术学院基础部，海南琼海571400；2.河北北方学院数学系，河北张家口075000）

设FFq是q个元素的有限域，其中q是素数的幂，FFnq是FFq上n维向量空间，用表示Gaussian系数，它可看做FFnq的m维子空间的个数.运用组合方法证明了几个已知的Gaussian系数恒等式，并给出几个新的Gaussian系数恒等式和它的组合方法证明.

恒等式；组合方法；Gaussian系数；有限域；子空间

1 预备知识

设FFq是q个元素的有限域，其中q是素数的幂，并且FFnq是FFq上的n维行向量空间，在文献［1］中，Gaussian系数用表示，它可看做的m维子空间的个数.文献［1］给出一些Gaussian系数恒等式，在这里多采用代数方法来证明.本文对其中的一些恒等式给出了组合方法证明，并且给出几个新的Gaussian系数恒等式，同样采用组合方法给出它们的证明.在证明中也用到文献［2－3］中的一些方法.本文未介绍的名词和术语见文献［1，4－5］，并且引用文献［1，6］中的一些结果.

定义1［5］设m是非负整数，q≠1为复数，而x是未定元，令

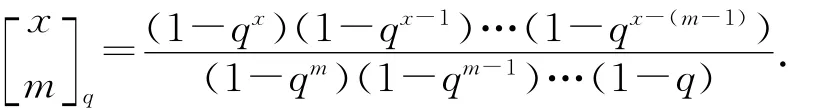
命题1［5］设m和n都是非负整数，q是素数的幂，那么FFnq中m维子空间的个数恰是

2 主要结果

命题2［4］设0≤m≤n，那么

命题3［1］设0≤m≤n，那么

其中系数al是l的分拆数（见文献［2］），l的Ferrers图适合规模m（n－m）的方格.

由命题2和命题3，可得下面的结论.

定理1［1］设0≤m≤n，那么

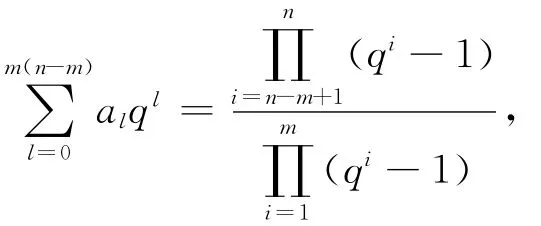
其中al是l的分拆数，l的Ferrers图适合规模m（n－m）的方格.

定理2 设k，m，n是非负整数，并且min｛m，n｝≥k.那么

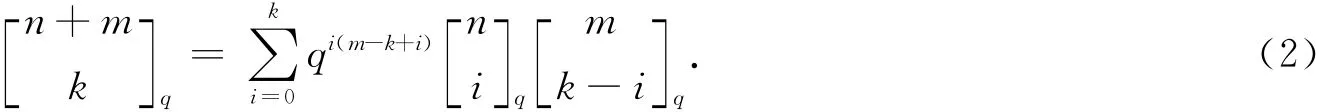
证明 设A是FFq上秩为k的k×n矩阵，那么A合同于阶梯形矩阵：

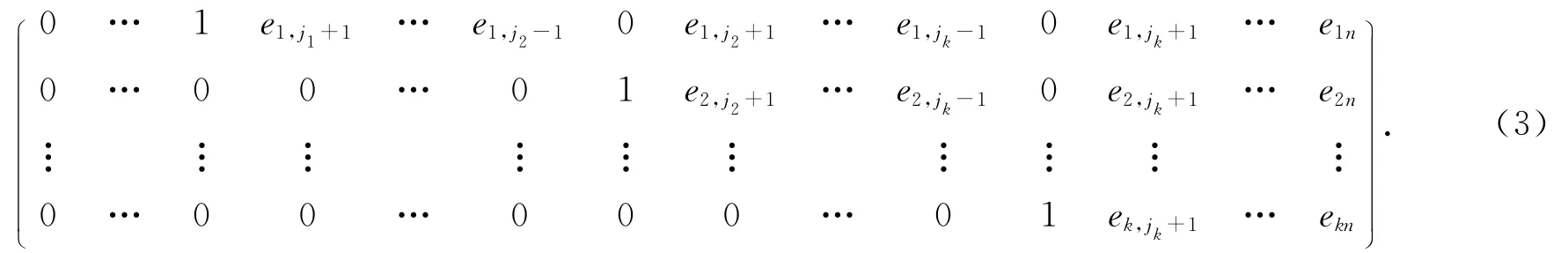
令M（j1，j2，…，jk）是矩阵表示为（3）的FFnq的k维子空间的个数，由阶梯形矩阵表示的唯一性，那么

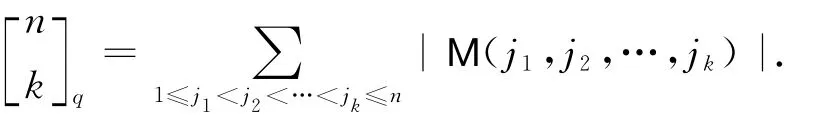
因为

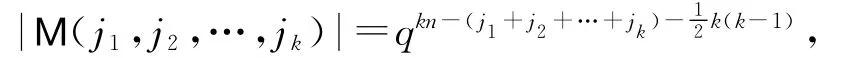
所以

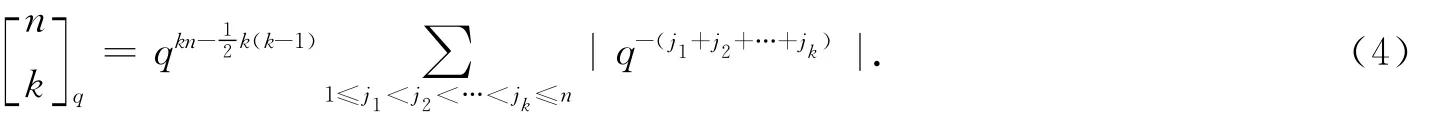
由（4）式可得

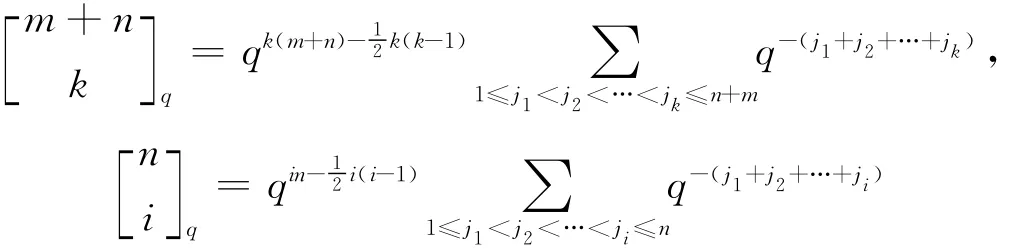
和

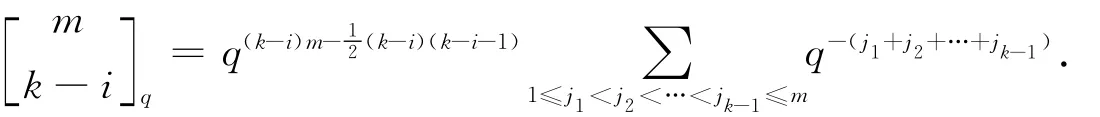
因而

因此（2）式成立.

推论1 设0＜k≤n＋1，那么

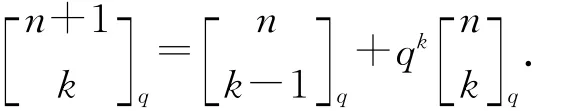
推论2 设0＜k≤n，那么

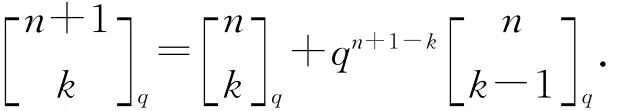
推论3 设k，n是非负整数k≤n，那么

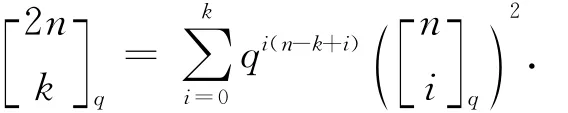
由文献［3］中的定理2.1，有如下命题.

命题4 设0≤k≤n，那么FFq中秩为k的n×n矩阵的个数是

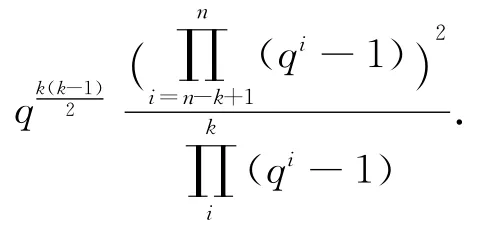
定理3 设0≤k≤n，那么

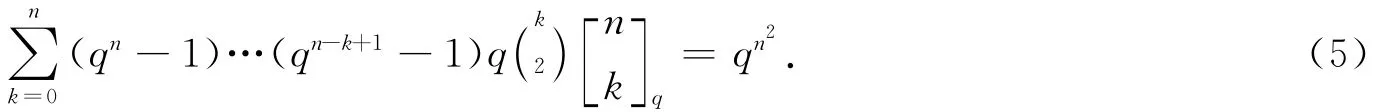
证明 考虑FFq上n×n矩阵（aij）1≤i，j≤n的个数.显然，（5）式等号右边是FFq上矩阵（aij）1≤i，j≤n的个数qn2.

因为（aij）1≤i，j≤n的个数＝n×n矩阵中0矩阵的个数＋秩为1的n×n矩阵的个数＋秩为2的n×n矩阵的个数＋…＋秩为n的n×n矩阵的个数.由命题4，可得

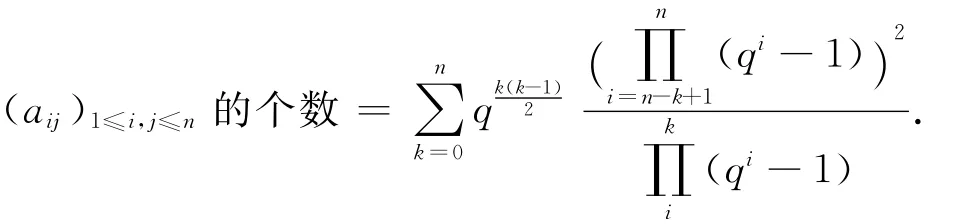
再由（1）式，有

它是（5）式等号的左边，因此（5）式成立.

命题5［1］设0≤m≤n，那么从到m维向量空间U的满射线性变换的数目是

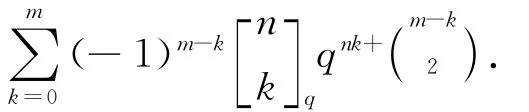
定理4 设0≤m≤n，那么FFq上秩为r的m×n矩阵（aij）1≤i，j≤r的数目是

证明 设W是m维向量空间U的一个r维子空间，把W的一个基β1，β2，…，βr，扩张为U的基β1，β2，…，βr，βr＋1，…，βm.令σ是FFnq到W的一个满射线性变换，使得σ（αi）＝βi，1≤i≤r，那么σj（r＋1≤j≤n），可由σ（α1），σ（α2），…，σ（αr）线性表示.我们可把σ看做FFnq到U的一个满射线性映射，所以

考虑到σ（α1），σ（α2），…，σ（αr）线性无关，所以矩阵（aij）1≤i≤m，1≤j≤n的前r列线性无关，而它其余的列向量可由其前r列线性表示，所以rank（aij）＝r.

反之，设rank（aij）1≤i≤m，1≤j≤n＝r，不妨设（aij）1≤i≤m，1≤j≤n的前r列线性无关.令σ（αl）由（7）式线性表示，那么σ（α1），σ（α2），…，σ（αr）线性无关，向量组σ（α1），σ（α2），…，σ（αn）可由σ（α1），σ（α2），…，σ（αr）线性表示，所以σ是FFnq到U的r维子空间W＝〈σ（α1），…，σ（αr）〉的一个线性变换（满射）.因此，FFnq到U的一个r维子空间满射线性变换σ，在FFnq和U的一个r维子空间取定基后，σ与秩为r的矩阵（aij）1≤i≤m，1≤j≤n之间是一一对应的.由命题5可得，FFnq到U的一个r维子空间满射线性映射数目是

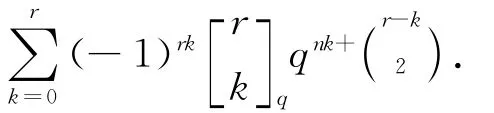
定理5 设0≤m≤n，那么

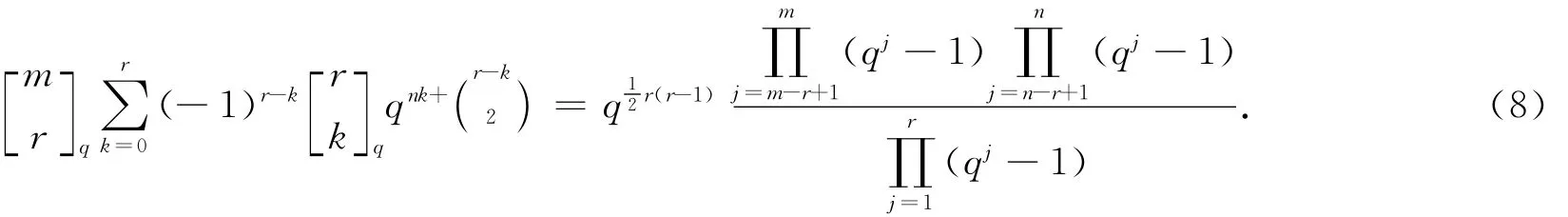
证明 由文献［2］中定理2.1，FFq上秩为r的m×n矩阵的数目是

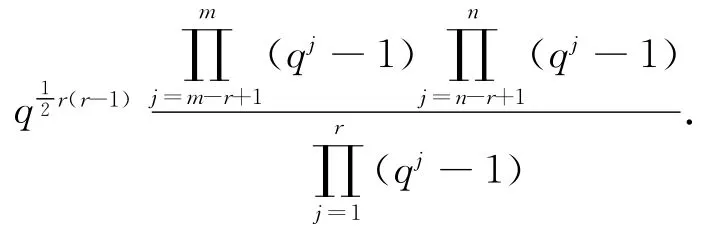
再由定理4，有（5）式成立.因此（8）式成立.

命题6 设n≥1，那么

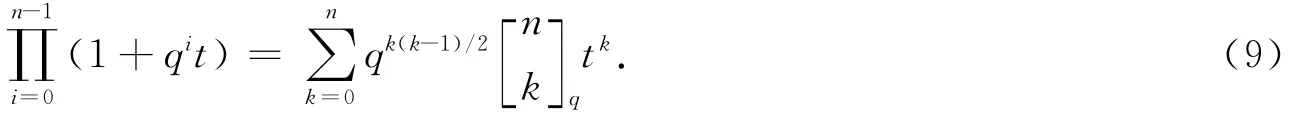
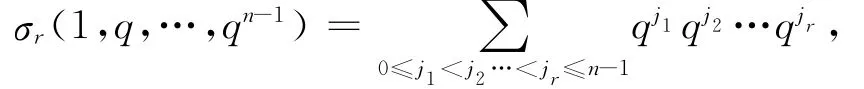
上式右端恰好是（9）式左端tr的系数.

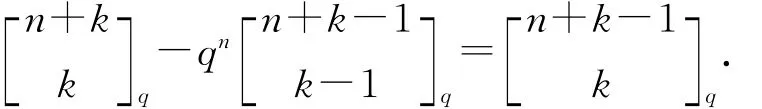
证明

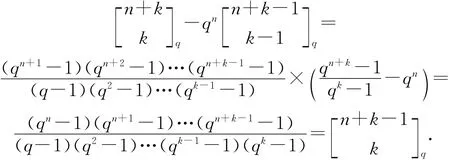
定理8 设k是非负整数，n是正整数，那么

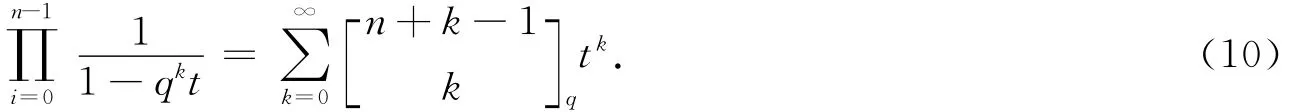
证明 对n施行数学归纳法，当n＝1时，

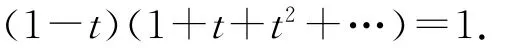
假设n＝l时，（10）式成立.我们来证明n＝l＋1时，（10）式成立.因为

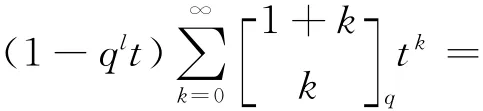
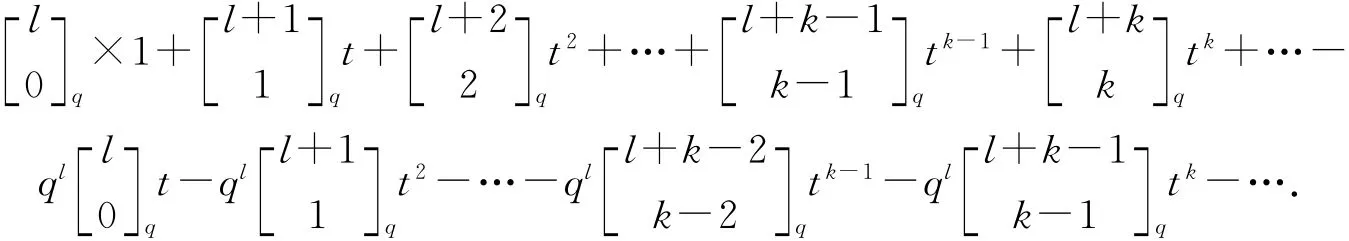
由定理7和归纳假设可知，上式右端等于

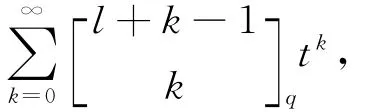
即

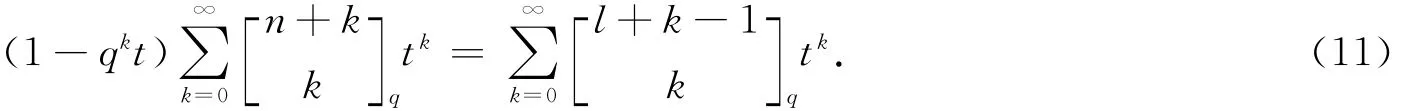
由归纳假设，有

所以，由（11）和（12）式，有

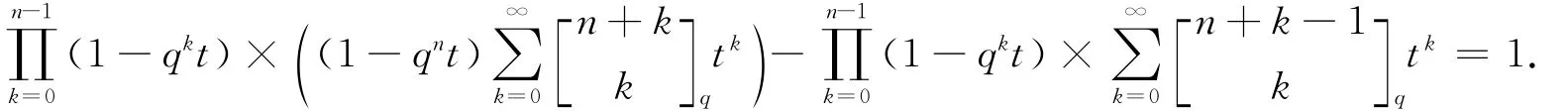
因此，（10）式成立.

令

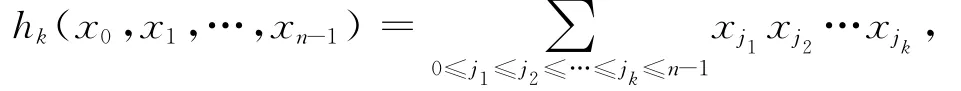
那么

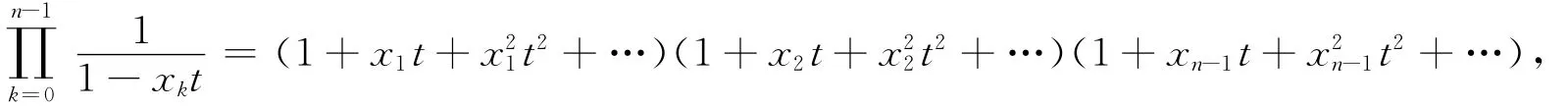
上式右端tk的系数数目是hr（x0，x1，…，xn－1），令x0＝1，x1＝q，…，xn－1＝qn－1，那么由定理8有下面的结论.

推论4 设n是正整数，k是非负整数，那么

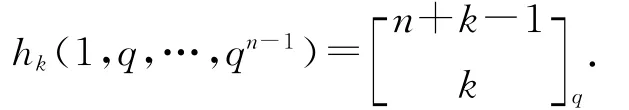
［1］ VAN LINT J H，WILSON R M.A course in combinatorics［M］.Second Edition.Beijing：China Machine Press，2004：325－350.

［2］ 宋元凤，南基洙.利用有限域上Ⅱ－Jordan型幂零矩阵构造Cartesian认证码［J］.东北师大学报：自然科学版，2012，44（3）：37－42.

［3］ YANGXIAN WANG，YUANJI HUO CHANGLIMA.Association schemes of matrices［M］.Beijing：Science Press，2011：36－51.

［4］ WAN ZHEXIAN.Geometry of classical groups over finite fieldsb second edition［M］.Beijing，New York：Science Prees，2002：1－7.

［5］ 陈修焕.恒等式的几何意义及其组合证明［J］.数学的实践与认识，2008，38（22）：181－184.

［6］ 钟裕林，霍元极.奇异典型群作用下子空间轨道的长度［J］.东北师大学报：自然科学版，2012，44（1）：36－40.

Several identity and their combination method is proved

ZHOU En1，HUO Yuan－ji2
（1.Department of Basic，Hainan College of Software Technology，Qinghai 571400，China；2.Department of Mathematics，Hebei North University，Zhangjiakou，075000，China）

LetFFqbe afinite field with q elements，where q is apower of aprime andFFnqbe the n－dimensional row vector space，and denote the Gaussian coefficient bywhich as numbers of subspaces overFFq.First，proved several Gauusian coefficient identity with the combinatorial method，then several Gauusian coefficient identity are given and their proofs with the combinatorial method.

identity；combinatorial method；Gaussian coefficient；subspace；finite field

O 153 ［学科代码］ 110·21

A

（责任编辑：陶 理）

1000－1832（2014）02－0040－05

10.11672／dbsdzk2014－02－009

2013－03－04

海南省自然科学基金资助项目（113009）.

周恩（1963—），男，教授，主要从事代数组合论研究.