物理常数在教学中的价值分析

孙 艺 袁海泉 孔如燕

(苏州大学 江苏 苏州 215006)

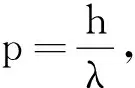
物理常数的教学对完善学生的知识结构具有重要作用．虽然物理常数在物理学发展中的“经典案例”时常被物理教师引用于激发学生学习物理的兴趣，但在以知识结构为逻辑构建的教材中，物理常数表现出的零散性，客观上弱化了物理常数在教学中的地位， 使物理常数的教学存在无意识性和缺乏物理特性等问题．物理常数的教学价值还没有得到充分认识，在培养学生的物理素养和物理能力中，物理常数还没有起到应有的作用．本文从串联教学内容、拓展研究方法、引入物理学史、深化物理实验、强化计量单位等方面分析了物理常数的教学价值．

1 串联教学内容

虽然物理常数在以知识结构为逻辑构建的物理教材中具有相对的零散性，但是物理常数在整个物理知识体系中占有重要地位．它不仅串联了物理知识点，而且还连接了物理知识类．例如：

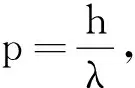
(2)阿伏伽德罗常数NA=6.02×1023mol-1通过法拉第常数F=eNA连接了宏观世界与微观世界；

(4)电磁波传播速度与光波传播速度之间出乎意料的惊人相符，使麦克斯韦立即意识到光波就是电磁波．于是，以光速c为桥梁把光学与电磁学统一了起来．

物理教学中，物理常数不仅是教学内容的一部分，也是不同教学内容的连接点．例如，牛顿万有引力中常数G=6.67×10-11N·m2·kg-2，G以待定系数的方式出现，确定了万有引力各个物理量的数学关系．同时，还通过卡文迪什(Henry Cavendish，1731～1810)的扭秤实验，联系测出G的具体数值的实验方法．另外，通过万有引力常数G建立的万有引力定律和由静电力常数k建立的库仑定律的比较联系“点电荷”与“质点”的模型和理想模型方法；对万有引力定律和库仑定律的比较，明确它们之间的区别与联系，有利于纠正错误概念，形成层次清楚的认知结构．

2 深化物理实验

对某一基本物理常数，无论是物理内涵的不断丰富，还是数值精确度的不断提高，不确定度的不断减少，都离不开物理实验，实验是基本物理常数研究中最重要的手段，它对物理常数的提出、验证和发展有着决定性的意义．如经典的物理实验有：测量引力常数G的卡文迪什扭秤法实验、测量光速c的迈克耳孙多面棱镜法实验、测量基本电荷e的密立根油滴实验以及测量阿伏伽德罗常数NA的德斯纳兹、X射线光学干涉术实验等等，这些实验构思之巧妙、方法之简洁、数据之精确都堪称物理实验的楷模．对这些实验的科学分析，不仅能使学生了解经典实验的设计思想、实验的过程和实验方法与技巧，而且能够为学生提供学习的感性材料和科学的思维方法，使学生加深对基本知识的认识程度，激发学生的求知欲，培养学生的探索能力．

物理常数测量在提供一组准确而可靠的物理常数值的同时，还证实了自然界的结构和运动是否存在内禀的恒常性和精确性，这推动了物理实验的改进和发展．主要有：

(1)物理常数与测量设备和环境的相关性，促进物理实验持续改进．如自1798年卡文迪什扭秤实验，首次测得G=6.754×10-11N·m2·kg-2以来，因引力的不可屏蔽性，使得G的测量实验至今还在改进；

(2)物理常数的精确性要求和非恒常性猜测，促进物理实验原理和方法的不断更新．如有着近370多年历史的光速c测量，先后经历了力学方法、天文学法、光学方法、电子学方法和激光方法[1]．

物理常数测量方法的多样性也联系了中学物理不同的知识内容．同一实验用不同的方法实现可以拓展学生的思路，加强学生举一反三和思维迁移的能力．例如，重力加速度g的测量就有多种方法，最主要的有：

方法一：直接用弹簧秤称出物体重力G，再用天平称出物体质量m，可得g；

方法二：利用物体的自由落体运动规律或平抛运动规律，设计实验，测量计算；

3 拓展研究方法

对物理常数的研究，展现出许多物理学研究问题的典型方法，其中科学假说法、理想实验法和类比综合法显得尤为突出．如普朗克常数h的产生最初就是起源于实验和理论的矛盾而提出的科学假设，玻尔沿袭普朗克和爱因斯坦的思想提出量子化假设解释了氢原子光谱；玻尔利用类比综合法在量子假设的基础上给出了氢原子光谱线系公式，德布罗意用类比法把波粒二象性推广到一切实物粒子，薛定谔用类比综合法建立了波动力学；而海森堡利用理想实验说明不确定关系式，玻尔和爱因斯坦也用理想实验为理论的完备性进行了长达40年之久的论战．

光速的测量由来以久，它的测定方法从两个不同的方向发展, 一种是天文学方法,另外一种是物理实验的方法．在对光速c精确测量的过程中产生了不同的研究方法．在过去一百多年中，研究者用不同方法做了数以百计的c的测量，目前公认的数值是c=(2.997 925±0.000 001)×108m/s[2]．

不断发展的研究方法可以带来物理学的巨大进步．同时总结、学习物理常数的研究方法对物理知识的掌握具有重要指导意义．例如，卡文迪什扭秤实验测万有引力常量G，就用到了转换法和微小量放大法．用打点计时器测重力加速度g时，纸带数据处理可以利用图像法，作v-t图，根据图像的斜率求出重力加速度值．在常数教学中教师可以渗透科学方法的教育，培养学生运用科学方法和科学思维分析问题、解决问题的能力．

4 强化计量单位

物理量之间通过各种物理定律和有关的定义彼此建立联系，人们往往取其中的一些作为基本物理量，以它们的单位作为基本单位，形成配套的单位体系，其他的单位可以由此推出，这就是单位制[3]．

有一些基本物理常数的定义和取值是与单位制的形成过程和确定标准有关的．如真空中的光速c，电常数ε0和磁常数μ0，原子质量单位u，电子伏特eV等．电磁学中的单位和单位制几经变革，走过了一条曲折的道路．电磁量实际上可以由两个互不相容的方程系来描述．因为两个库仑定律都可以作为定义性方程，一个是静电学的库仑定律，一个是静磁学的库仑定律．于是出现了两种“绝对”电磁学单位制，即厘米-克-秒静电单位制(CGSE)和厘米-克-秒电磁单位制(CGSM)．在CGSE和CGSM两种单位制中，介质电容率ε和磁导率μ是两个相对应的物理量．在CGSE制中，ε为无量纲的纯数，而μ有量纲；在CGSM制中则正好相反．为了解决绝对静电单位制和绝对电磁单位制的矛盾，高斯提出了混合单位制．其基本出发点是，所有的电学量都用CGSE单位，而所有的磁学量都用CGSM单位．于是在真空中取ε0=μ0=1，即ε和μ均为无量纲的纯数．对于同时包含有电学量和磁学量的公式，则需增加与真空中的光速c有关的系数．

5 引入物理学史

著名物理学家郎之万曾经说过“在科学教学中，加入历史的观点是有百利而无一弊的．”每一个物理常数的背后，都有很多的故事．在物理教学中，使学生了解物理常数的由来，实验测定的方法和过程，能够大大激发学生了解自然，探索自然的兴趣，给学生以启迪，也符合新课标，新教材的教学思想．

如在讲万有引力定律时，对引力常数G的测定，采用引入物理学史的教学，学生对G印象较深刻，也容易记牢．关于确定万有引力常数G的数值，1798年，英国物理学家卡文迪什做了第一个精确的测量．实验装置中，将两个质量为m的小球固定在一根轻质细杆的两端，用一根细金属丝将杆吊起．将两个质量为M的大铅球等距离放置于两小球近旁，相邻的大球和小球之间的万有引力吸引着它们彼此接近．这使得细杆要转过一个角度，从而引起金属丝发生扭转，直到金属丝的弹性恢复力产生的转矩与万有引力产生的扭转矩相平衡时为止．金属丝的扭转角度是通过固定在它上面的一面小平面镜所反射光线的偏转来表现的．通过计算所求得的弹性恢复力F与万有引力大小相等，只要量出大小铅球球心间距离r，由万有引力公式可求得G值．当时测得的G值为6.63×10-11N·m2·kg-2．这一结果比现在公认的值约小1%，这是略去杆的转动惯量而产生的误差．G是人类最早进行实验测量的一个基本物理常数，但由于地球引力的影响却是测量得最不精确的一个．

重现物理学史的意义不仅在于现在中学生犯的错误往往就是人类物理学史上的错误认识，这对重视学生的错误是大有裨益的，而且物理知识的很多内容都有历史事实或名人轶事或趣闻笑话，教师从中选出合适部分用于教学，对激发学生兴趣，提升他们的思维和引入新知识都有明显的效果．

6 结束语

物理常数丰富的教学内涵, 因物理常数本身的难以解释和我们注重知识逻辑体系的习惯性思维,而没有得到充分的发掘，本文从中学基础物理课标提出的三维课程目标，即知识与技能、过程与方法、情感态度与价值观出发，提出了以上5条物理常数的教学价值，旨在让物理常数相关知识的教学得到重视并在中学物理教学中发挥应有的作用．为此物理教师需要从积累和总结物理常数教学的资料着手, 进行教学方法和途径的探索．

参考文献

1 陈华.浅论物理常数教学.浙江万里学院学报，2008,21(5)

2 蔡家宗.物理常数与科学研究.玉林师专学报(自然科学，1997,18(3)

3 杨建平,李兴鳌.基本物理常数与物理学史.现代物理知识，16(1):18～19

4 陈华，关于物理常数的科学解释与哲学思考.物理通报，2013(10):115～120