“微元法” 巧解两道2013高考物理压轴题

马力力

(华北油田第五中学 河北 廊坊 065007)

在处理物理问题时，从对事物的极小部分(微元)的分析入手，达到解决事物整体问题的方法，叫作微元法．微元法在近几年物理高考中崭露头角，体现出它独特的解题魅力，并逐渐为广大高中教师所重视．2013年高考全国理综新课标卷Ⅰ与高考天津卷的压轴题，都运用了微元思想．

笔者以这两道题为例，剖析微元法之妙用，以期让高中生在思维上拓展更广阔的空间，也希望广大教师注重课堂上进行物理科学方法的培养．

1 高考试题例析

运用动量定理“微元法”求解2013年高考全国理综新课标卷Ⅰ第25题．

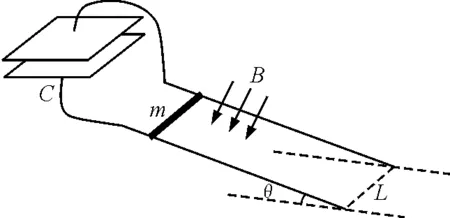
图1

【例1】如图1，两条平行导轨所在平面与水平地面的夹角为θ，间距为L．导轨上端接有一平行板电容器，电容为C．导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面．在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触．已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g．忽略所有电阻．让金属棒从导轨上端由静止开始下滑，求:

(1)电容器极板上积累的电荷量与金属棒速度大小的关系；

(2)金属棒的速度大小随时间变化的关系．

解析：(1) 设金属棒下滑的速度大小为v,则感应电动势为

E=BLv

平行板电容器两极板之间的电势差为

U=E

设此时电容器极板上积累的电荷量为Q，按定义有

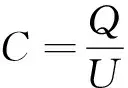
联立得

Q=CBLv

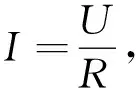
在时间间隔(t，t+Δt)内，由动量定理得

FΔt=mΔv

所以

(mgsinθ-μmgcosθ-Bil)Δt=mΔv

∑(mgsinθ-μmgcosθ-Bil)Δt=∑mΔv

设在时间间隔(t，t+Δt)内流经金属棒的电荷量为ΔQ，则

则

mgtsinθ-μmgtcosθ-B2l2Cv=mv

为所求．

2 如何在教学中渗透“微元法”

2.1 新课教学提高认知 渗透微元思想

微元法既是一种深刻的思想方法，又是解决问题的巧妙操作方法，它以物理学的力、电、热、光等领域为载体，以近似、对称、等效、数列、极限、积分、归纳等多种数学方法为手段，实现化曲为直、化变为恒、化繁为简，于微元法中解决变量物理问题的目的．

微元法思想在新课标教材(人教版)中多次出现，《物理·必修1》第一章就有所渗透．在引入瞬时速度概念时，教材提出从t到t+Δt这段时间间隔内，Δt越小运动的描述就越精确．当Δt趋向于零时，Δt的平均速度就认为是t时刻的瞬时速度．这也是数学中的微分思想．教师在教学时应以此为契机，提出Δt就是选取的“微元”，先将瞬时速度变化问题转化为平均速度变化问题，再利用数学微分知识，将平均速度问题转化为瞬时速度问题．又如，再讲变力做功图像法时，F-x图像为一条不规则曲线，计算可以将位移分成许多很短的间隔Δx，由于每一段Δx都很小，就可以将每一段位移对应的力F近似地看成恒力，这样就能利用功的定义式计算出每一小段内外力的功，再累加得到整个过程变力所做的总功，即为图线与横轴所围成的面积．其中Δx为所取的“微元”，将变力做功转化为恒力做功，再利用数学中的积分思想由图像面积求出变力做功．

在推导匀变速直线运动的位移公式；“弹性势能”中求弹簧弹力做功；安培分子环形电流假说；由洛伦兹力推导安培力公式等教学中，都可以渗透“微元法”思想．教师应该充分利用教材中资源，抓住每个契机，提高学生认知，在潜移默化中让学生顺理成章，自然地接受这种科学方法．

2.2 复习课中精选习题 总结微元法解题技巧

任何一种科学方法的运用都离不开习题，教师在复习课中，要善于精选习题，精讲精练，并根据习题特点指导学生自己总结微元法的解题技巧．提高学生敏锐的观察力、选择正确方法的判断力和迅速解题的数学能力．微元法处理问题的主要环节一般为两点：一是取“微元”，即对整体对象做无限分割，分割的对象可以是各种几何体或各种物理量，从而得到选取的“元”．如线元、角元、面积元、质量元、时间元、位移元、功元、电流元等等，它们均具有整体对象的基本特征；二是对微元进行数学方法(如微分、积分、数列等)、物理思想(如牛顿定律、动量定理、动能定理等)处理．即从事物的极小部分(微元)分析入手，达到解决事物整体问题的目的．

下面以2013年高考天津理综卷第12题压轴题为例，说明微元法的运用．

【例2】超导现象是20世纪人类重大发现之一，目前我国己研制出世界传输电流最大的高温超导电缆并成功示范运行．(1)略．

(2)为探究该圆环在超导状态的电阻率上限ρ，研究人员测得撤去磁场后环中电流为I,并经一年以上的时间t未检测出电流变化．实际上仪器只能检测出大于ΔI的电流变化，其中ΔI≪I，当电流的变化小于ΔI时，仪器检测不出电流的变化，研究人员便认为电流没有变化．设环的横截面积为S，环中定向移动电子的平均速率为v，电子质量为m,电荷量为e．试用上述给出的各物理量，推导出ρ的表达式．

解析：原题标准答案运用能量守恒求解(略)．这里改用动能定理微元法．

当定向移动电子的平均速度发生变化就会引起环中电流变化．电流变化大小为ΔI，相应定向移动电子的平均速率变化的大小为Δv,则ΔI=neSΔv取一小段时间Δt(选取适当的微元)，则在时间间隔(t，t+Δt)内，由动能定理(采用恰当的物理思想)，得

W电=ΔEk

忽略高阶小量(数学处理方法)，其中

则

∑I2RΔt=∑MvΔv(运用数学积分思想)

得

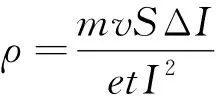
为所求．

显而易见，微元法的精妙之处也是它的难点所在．其一，判断习题是否适用微元法就是一个难点；其二，微元的选择是否恰当将直接影响解决问题的成败．取微元，对整体对象做无限分割是微元法的灵魂所在，微元对象必须既有整体事物的本质特征，又能派生作为无穷小量所能发挥的特别功能；其三，微元的处理过程对学生的物理思维和数学功底要求更高．这也是微元法区别其他普通物理方法的显著特点、精彩之处．

2.3 思想上予以重视 突出培养学生科学方法创新思维

其实高考物理试题出现微元法的应用并不陌生，江苏省2006年到2009年这4年来高考物理卷中的最后一题，都与电磁感应知识点相关，在标准答案中，都是用微元法求解．然而目前微元法往往只在奥赛教学中讲解，一般普通高中并不讲或者仅仅是点到为止．所以大部分高中生遇到这类问题都束手无策，对待这类高考压轴题都采取放弃策略．高中教师不愿意花时间讲解微元法主要原因是这种方法对学生的物理能力、数学能力要求相对较高，大部分高中生接受起来感到困难,效果不好．

如今高考压轴题的分值往往在20分左右，其目的既能考查学生的物理能力，也有利于重点院校选拔人才，是区分普通优秀生与最优秀生的主要题目．针对重点院校或者能力较强的优等生，教师不仅仅是在高三复习中讲解高考试题渗透微元法教学，更重要的是教师要从思想上予以重视，充分利用教材所提供的素材,在平常的教学中突出各种科学方法的渗透，重视开展学生的各种探究活动、实践活动,启迪学生的创新思维，培养学生的综合能力．特别是要重视运用数学知识与物理思想相结合，解决实际问题的能力．让学生体会“山重水复疑无路，柳暗花明又一村”的喜悦，为我国重点大学院校输送新时代优秀人才．