逐差间隔数对处理结果准确性影响实验研究

高志华 孙迎春

(东北师范大学物理学院 吉林 长春 130024)

1 引言

逐差法是物理实验数据处理的常用方法[1]，适用于函数为多项式形式且自变量等间隔变化的实验数据处理．逐差法分为相邻逐差和隔项逐差，故对同一组实验数据可以求得多种逐差结果．关于逐差法处理实验数据的准确性一直存在争议．通常，相邻逐差被认为是不合理的，因为在实际数据的处理过程仅用到了首尾两个数据，中间的数据都没用上，即没有充分利用实验数据，被认为不能很好地消除随机误差[2]．多数学者认为，如果测量数据个数是偶数，最好是把数据对半分，后一半数据减去前一半相应的数据，这样可以充分利用测量数据，更好地消除偶然误差[2～4]．有人认为逐差法处理实验数据不科学[5,6]．目前，关于逐差法的误差计算和分析方法存在很多分歧，文献[1]认为可以利用多次测量的随机误差统计分析方法来计算，这种计算如果数据量小的情况下就不能使用随机误差统计公式，还有这种方法求的是求差后的数据的随机误差，它和测量数据的统计误差也没有非常明确的关系，也就是说求差后，随机误差有可能减小了(同号)，也可能增加了(异号)．文献[2～4]对不同间隔逐差的误差进行了理论计算和证明，在计算误差时取每次测量的偶然误差均为仪器误差限，而且都取为正，这种方法会导致使用数据越多，整体误差越大，不仅没有起到消除随机误差的作用，还增加了误差，正如文献[5]所说利用这种误差计算方法使用数据量少反而误差越小．显然上述误差计算分析方法都不具备严格的合理性．定性的讲，对一个量进行多次测量会在一定程度上减少随机误差，但能减少多少没有一个严格的标准，使用数据少，结果会过分依赖某个数据的准确性，误差范围无法控制．所以，到目前为止关于逐差法的误差分析还没有达成统一的结论．

本文结合声速测量、电阻测量和弹簧弹性系数测量实验的数据处理结果，就逐差法的逐差间隔(使用数据量)对处理结果的准确性影响进行了对比、分析和总结．

2 声速测量数据处理

本文利用驻波法进行了声速测量实验，仪器是学生实验用超声声速仪．测量方法采用振幅极值法(下简称法1)和相位比较法(下简称法2)．振幅极值法测量的是相邻波腹距离(半波长)，相位比较法测量的是相邻同相点的间距(波长)，再根据声速公式v=fλ求出声速．本文对测量数据进行了不同间隔逐差方式处理并将声速计算结果和声速理论值进行了比较，得到了各种间隔逐差方式的误差分布情况．

实验条件：温度为12.0℃，相对湿度为43%，饱和蒸汽压为10.518 mmHg,频率为f=40.39 kHz．

根据理论声速计算公式

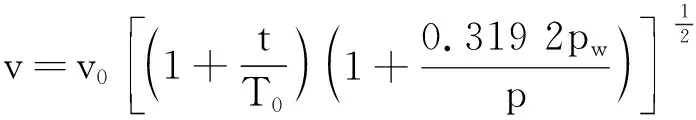
其中v0=331.45 m/s，pw为空气中水蒸汽分压强，等于空气中的水蒸汽的饱和蒸汽压和相对湿度的乘积，p为大气压强，可得理论声速v=338.974 m/s.

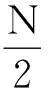
表1 驻波法测量声速实验数据

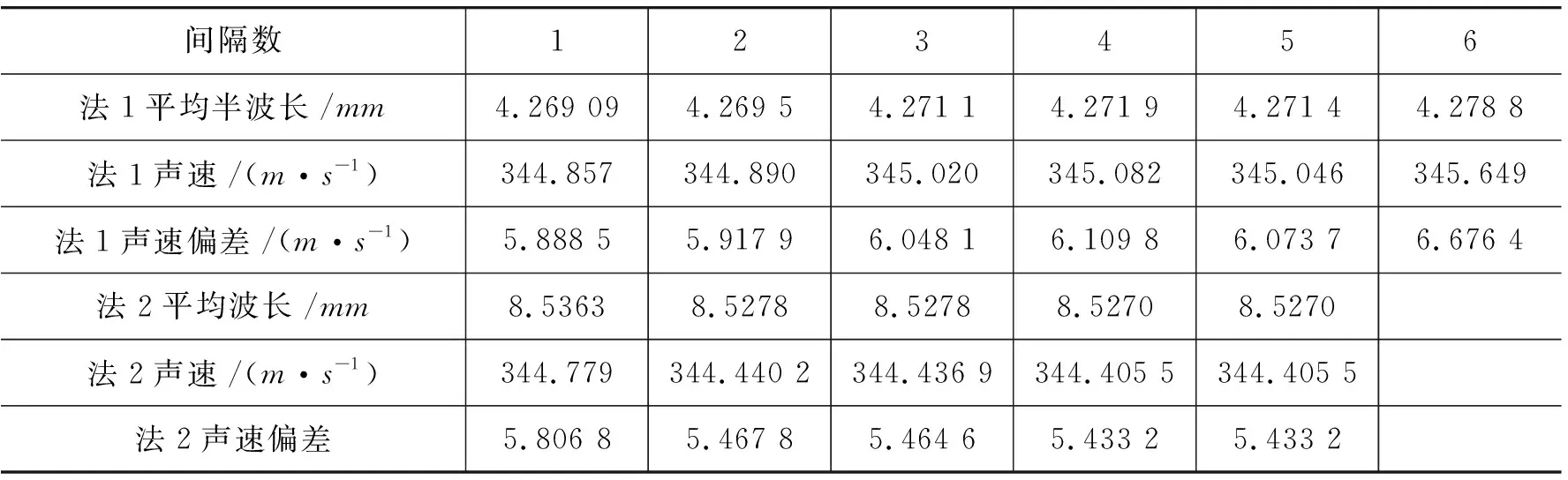
表2 法1和法2采用逐差法处理实验结果

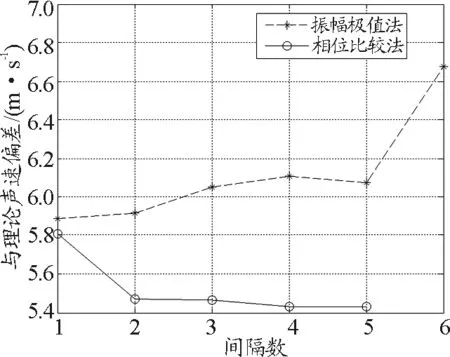
图1 法1和法2的不同逐差间隔计算声速相对理论声速偏差曲线

表2和图1表明,就振幅极值法而言，间隔1的结果与理论值结果最为接近，而间隔6的结果偏差最大，其他间隔的计算结果间差异不明显，这种结果与文献[2～4]的预测不一致．由于相邻振幅极值间距差没有随发射-接收端距离增加而明显变化，因此，间隔6的结果不是因为发射-接收端距离改变造成的．就相位比较而言，间隔1的计算结果与理论值的差异最大，间隔4或5的偏差最小，间隔2，3，4和5的计算结果偏差较为接近，表明，逐差间隔增大偏差减小，与文献[2～4]分析的结果基本一致．就两种测量方法而言，相位比较法测得的声速更接近理论值，而且，不论逐差间隔多大，相位比较法的声速偏差普遍比振幅极值法小．

可见，在声速测量实验数据处理中，不同逐差间隔对处理结果的影响在两组测量数据处理中没有明显的规律性，而不同测量方法得到的结果的准确性有明显的差异．

3 伏安法测电阻及弹簧振子劲度系数测量数据处理

为了得到逐差间隔对处理数据处理结果的影响规律，本文利用逐差法对文献[7]和文献[1]中的实验数据进行了处理和分析，结果如表3和图2所示．U为电压，I为电流．

3.1 伏安法测电阻实验数据及处理结果

表3 伏安法测电阻数据

表4 伏安法测电阻不同间隔逐差法处理结果

表4结果表明，不同逐差间隔与电阻的计算没有一致的规律性，结果可能小，也可能大，没有体现出文献[2～4]所说的规律性．

3.2 弹簧振子周期公式求劲度系数

表5 弹簧振子劲度系数测量实验数据

表6 不同逐差间隔计算弹簧振子劲度系数结果

表6处理结果表明，逐差间隔与劲度系数计算也没有一致的规律性．

4 不同逐差间隔结果与线性拟合结果的比较

表7 不同逐差间隔结果与线性拟合结果的比较

通过表7中不同逐差间隔与线性拟合结果的比较可知，间隔接近数据量一半的计算结果接近拟合结果的几率更大．其原因在于线性拟合的结果受到所有数据的影响，所以用到全部数据的逐差间隔应该更接近拟合值．如果以拟合值为准，则逐差间隔适当接近数据量一半可能会更好，但就某一次实验数据处理而言不能保证这一结果是最好的，只能说是较好的．

5 总结

通过对上面4组实验数据处理的结果可以看出，结果的准确性和逐差的间隔数(使用数据量)并不呈现明显的规律性，结果的准确性更多地依赖测量方法和测量结果的准确性，逐差法处理数据的适宜间隔随测量方法不同而不同，使用更多数据也不能保证误差是最小的，但可以保证误差相对较小．所以，前面提到的文献[2～4]对逐差法的误差计算的分析是不合理的，没有可靠依据．

通过前面的数据处理可以看出，对于伏安法测电阻和弹簧振子劲度系数测量中，逐差法得到的结果和线性拟合值还是比较接近的，但在声速测量中处理结果与理论声速偏差较大．可见，逐差法处理实验数据的误差主要来源于测量方法和测量过程本身，这种方法不能非常好地抵消测量过程中的随机误差，其中好的结果可以同线性拟合结果相当．相比于线性拟合方法，逐差法处理数据更为简洁，所以，在一些预测和估测实验和学生实验中还是值得应用的．但由于它本身不确定度难以计算，在精确测量中不能过分依赖这种方法得到的结果．

参考文献

1 龚镇雄.普通物理实验中的数据处理.西安：西北电讯工程学院出版社,1985.102～121

2 黄曙江.逐差法的较优分组.物理通报，1998(4)：7～9

3 钟纪琳.关于运用逐差法处理物理实验数据时逐差间隔的最佳选取问题.重庆建筑工程学院学报,1989，1(4):91～97

4 潘小青.逐差法及其应用探讨.大学物理实验，2010,23(2):86～87

5 北京市物理学会,北京市物理教学委员会专题组.“逐差法” 与实验测量数据的有效利用.物理通报,1998(10)

6 杨卫群.用逐差法处理数据不科学.大学物理实验,2001,14(2)：46～48

7 彭志华,段世政,宁艳桃.逐差法处理实验数据的研究.河南师范大学学报(自然科学版) ,2004,32(2):94～97