迈克尔孙干涉仪系统误差的估测

邓锂强

(广东石油化工学院 理学院 广东 茂名 525000)

1 引言

2 实验原理

迈克尔孙干涉仪是一种利用分振幅法产生双光束以实现干涉的仪器．图1为其光路示意图[2]．

图1 迈克尔孙干涉仪光路示意图

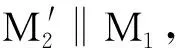
A点处S2，S1的光程差为[2,3]

Δ=2dcosθ

(1)

以入射角θ为圆锥母线的光束所形成的干涉条纹是一个圆环，在屏上就有一组半径不等的同心圆环，A点为亮环所对应的条件为

Δ=2dcosθk=kλ

(2)

当θ=0时，Δ最大，中心O点对应的级次最高

Δ=2d=kλ

(3)

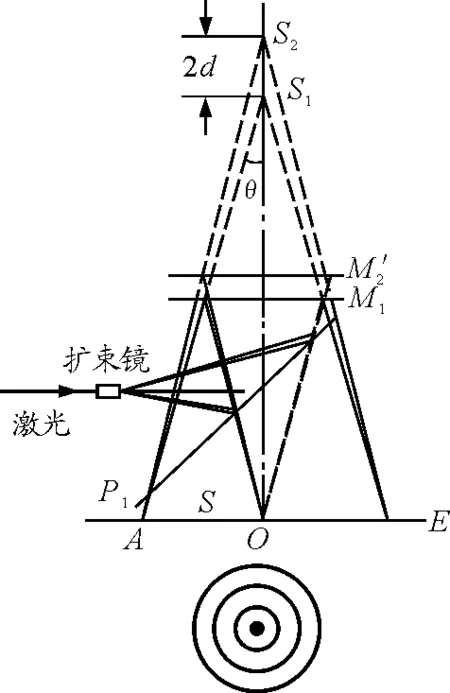
图2 非定域干涉图

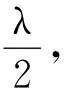
(4)

若已知光源波长λ和移动数N，可精确地测量长度Δd；如果测出Δd并数出条纹的移动数N，就可测光源的波长λ．

3 仪器误差分析

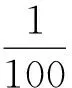
仪器传动机构对保证仪器的性能起着很重要的作用，它既要传动灵活、无窜动和卡死现象，又要有相当精度，其读数头部件如图3所示．丝杆的一端由一颗一级钢珠和磨光顶头紧密接触，粗动时转动粗动手轮、联动丝杆转动，同时带动读数盘，在读数窗上用3×放大镜观察．将读数盘套入小齿轮，再套入平面轴承，构成一个组件，然后再套入丝杆上，一端衬入压缩簧片，另一端须拧紧丝杆螺母，使蜗轮对丝杆产生一定的封闭压紧力．微动时，转动蜗杆，就能经蜗轮联动丝杆.为了减少多余的摩擦力，在粗动手轮轴壳内压入两只超轻系列滚动轴承，因此粗动、微动方便，灵活可靠[4]．

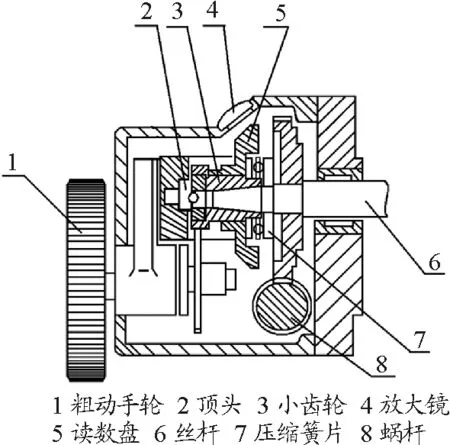
图3 读数头结构

迈克尔孙干涉仪的仪器误差主要由机械部件的精度决定，由下面7个部分组成[1，4]．

(1)丝杆、螺母的螺距误差

丝杆螺距为1 mm，采用1级螺纹副，与0～25 mm的1级螺旋测微计示值误差限相同．1级螺旋测微计的示值误差限为±4 μm，文献[5]给出了1级螺旋测微计示值误差限±4 μm的8个组成分量的参数，其螺旋副最大螺距误差Δs为±3 μm，故可取丝杆、螺母的螺距误差为±3 μm．

(2)螺纹副的重复性误差限约为1.4 μm．由于机械制造的公差限制，使得实验的传动与位移测量部件的准确度受到很大的限制．与1级螺旋测微计的特性相近，干涉仪单向移动趋近同一位置示值时的重复性误差限约为1.4 μm．

(3)丝杆轴向窜动

包括丝杆内顶尖孔和轴颈不同心，丝杆轴心线与顶头不垂直，丝杆轴颈的间隙，丝杆带动拖扳前进或后退时顶头受力不同产生的弹性形变，另外还有顶头接触处光洁度差，也会造成波动，合计总窜动量可达±7.6×10-5mm．

(4)导轨不直度，当条纹计数为100时，可产生±1.3×10-6mm的误差．

(5)读数误差

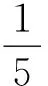
(7)由于螺纹副未采用消除空程的机构，实际使用中空程可能达到0.1 mm以上．

其中空程在实际测量中可以采取措施消除，可以不考虑．上面的6个系统误差分量中丝杆、螺母的螺距误差为远大于其他几个分量，是主要未定系差，在实验中可以作为迈克尔孙干涉仪的仪器误差，而忽略其他分量的影响．故迈克尔孙干涉仪的仪器误差可取为：ΔINS=±3 μm，这远大于测量中的随机误差，是测量误差中的主要部分．

4 调节使用不当产生的系统误差

4.1 M1与不严格平行

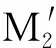
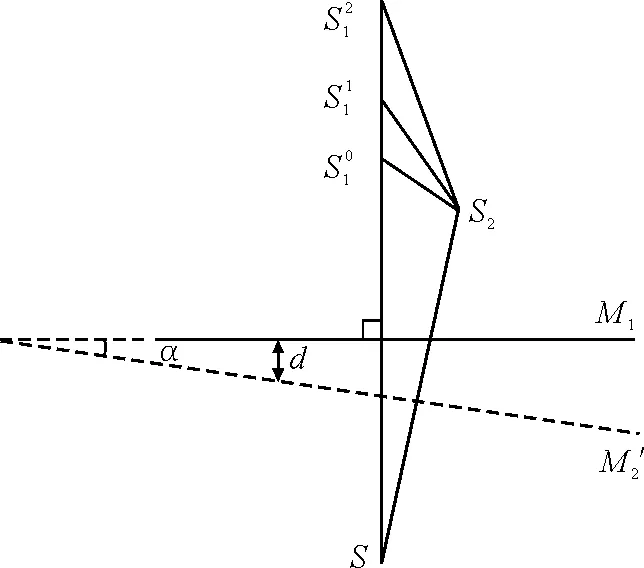
图4 M1与不严格平行

4.2 M1的法线方向与移动方向不一致

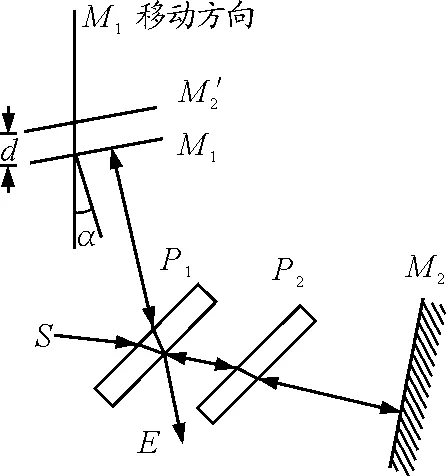
图5 M1的法线方向与移动方向不一致

通过对迈克尔孙干涉仪进行调整，使M1的移动方向与法线方向尽量一致，减小误差．调节方法：用一张画有“+”字的白纸罩在M1镜面上，用激光束射到“+”字中心，转动粗动手轮，使M1在导轨上移动，调节激光束的方位，使激光束始终打在中心位置，此时激光束与导轨(即M1移动方向)平行．取下白纸，以激光束为基准，调整M1后的三个螺丝，使入射光与反射光重合，此时M1的法线与其移动方向平行[7]．

5 系统误差的估测

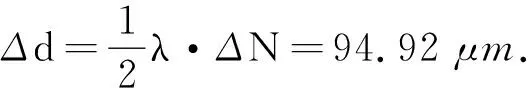
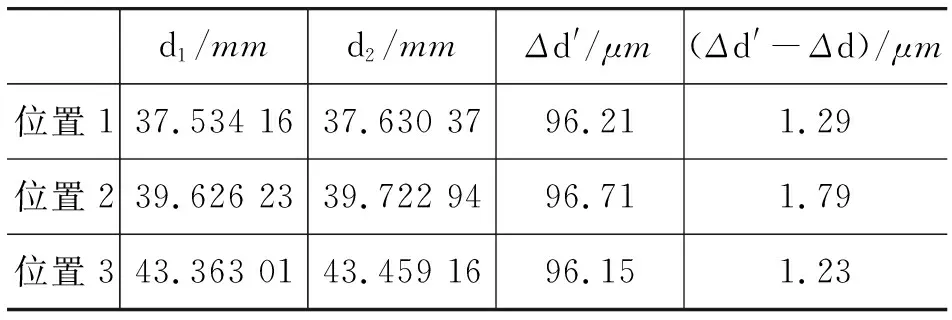
表2 迈克尔孙干涉仪二的系统误差估测

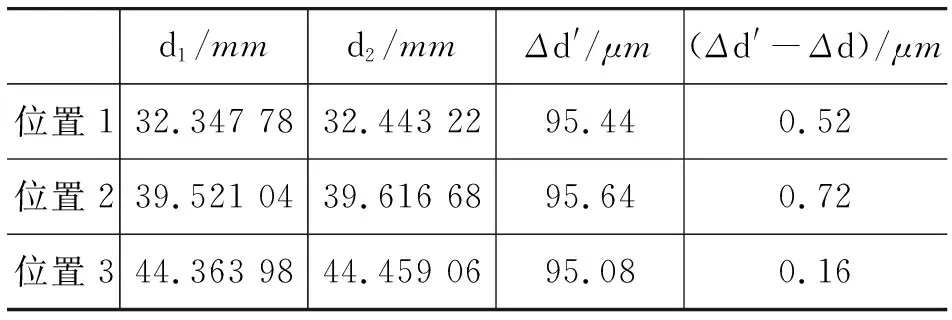
表3 迈克尔孙干涉仪三的系统误差估测

表4 另一厂家年限较长的迈克尔孙干涉仪的系统误差估测

从表1～4的数据可见，同一台仪器不同位置的系统误差的估测值Δd′-Δd不同，不同仪器的系统误差的估测值Δd′-Δd也不同，而且使用年限较长的一台仪器的系统误差估测值明显比其他仪器的系统误差估测值要大，这是仪器移动机构松动及磨损而产生的．从系统误差估测值Δd′-Δd可知，对于未经校准的迈克尔孙干涉仪，其仪器误差取为ΔINS=±3μm是可行的．

因为迈克尔孙干涉仪的系统误差较大，如何减小它的影响呢？

由公式(4)可得

(5)

表5 条纹计数与波长相对误差关系表

从表5可知，当条纹计数较大时，仪器误差引起的波长相对误差较小，为提高测量精度，可以增加条纹计数，一般条纹计数应该在300以上．

6 结束语

本文根据迈克尔孙干涉仪的机械结构，分析了构成仪器误差的7个分量，其中丝杆、螺母的螺距误差为远大于其他几个分量，是主要未定系差，忽略其他分量的影响，迈克尔孙干涉仪的仪器误差可取为：ΔINS=±3 μm，避免了部分教师把微动手轮最小刻度的一半或十分之一作为仪器误差的错误做法；分析了迈克尔孙干涉仪由于调节使用不当而产生的误差，对迈克尔孙干涉仪的系统误差进行了估测，根据估测的结果可知，对于未经校准的迈克尔孙干涉仪，其仪器误差可取为：ΔINS=±3 μm是可行的．

参考文献

1 朱鹤年.新概念物理实验测量引论——数据分析与不确定度评定基础.北京：高等教育出版社，2007.40～41

2 张昌莘，王德明，方运良.三级物理实验教程.北京：化学工业出版社，2010.170

3 曾金根，刘菘，戚小平.大学物理实验教程.上海：同济大学出版社，2002.183～185

4 严家彪，徐森录.迈克尔孙干涉仪研制中若干问题的探讨.光学仪器，1982，4(3)：25～28

5 朱鹤年.物理实验研究.北京:清华大学出版社，1994.123～124

6 马雪莲，刁永锋. 迈克尔孙干涉仪测波长的最佳区间的讨论.重庆工学院学报，2002，16(4)：32～33

7 王云霞，金本喜. 迈克尔孙干涉仪调节方法的改进.淮阴工业专科学校学报，1999，8(3)：30～31

8 郭长立. 迈克尔孙干涉仪影响因素的测量不确定度分析.实验室研究与探索，2010，29(7)：38～40