等效“平摆线”在物理解题中的应用——2013高考福建省物理压轴题和2013北约自主招生压轴题的思考

周 华

(长乐第一中学物理组 福建 福州 350200)

2013高考刚落下帷幕，今年福建省理科综合物理试题第22题和北约物理自主招生第12题相似，都不约而同地考查的是数学中的摆线问题；此前，2008江苏卷高考物理试题第14题也考查了摆线问题．摆线问题在物理竞赛和自主招生考试中是一个必备的知识点，只要参加过物理奥赛和自主招生培训的同学就会非常熟悉，最近在2011年第28届全国中学生物理竞赛复赛试卷第3题(渐开线)和第4题中(平摆线)有考查过．摆线是一类十分重要的曲线，可以分为平摆线、圆摆线、渐开线三大类．今年福建高考和北约自主招生考查的是平摆线，下面就对平摆线在物理解题中的应用做一个总结．

1 平摆线的数学定义和参数方程

摆线为奇妙的数学曲线之一，平摆线定义是：一个圆在一条定直线上滚动时，圆周上一个定点的轨

迹称为平摆线．也叫做“等时曲线”或“旋轮线”．如历史上著名的“最速降线”就是平摆线；在日常生活中，自行车、马车、火车等车轮上的任一点随车辆的前进而描绘出美妙的旋轮线．

如图1所示，为正在平直路面以速度v0匀速行驶的某车辆的一只轮子，轮子的半径为r，以轮缘上某时刻与地面的接触点A作为直角坐标系的原点，与v0方向为x轴，建立坐标系．经时间t，轮子转过的角θ, 此时轮缘A点的参数方程为

x=rθ-rsinθ

y=r-rcosθ

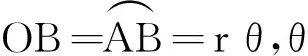
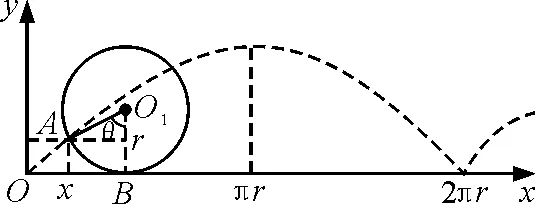
图1

2 平摆线的等效性运动学和动力学原理

对于平摆线在物理学中完全可以看作是“圆”在“直线”上滚动，即可将平摆线的运动可看成匀速直线运动和匀速圆周运动的合运动．而作为对应的渐开线，在物理学中完全可以看作是“直线”在“圆”上滚动，即可将渐开线的运动可看成匀速圆周运动和匀速直线运动的合运动．

根据力与运动的关系，在具体情况中，只要对物体运动进行受力分析，就能找出对应的匀速直线的分运动的合力为零，做匀速圆周的分运动受到一个大小恒定而方向不断随速度变化的向心力．

3 平摆线原理在物理解题中的应用

下面就以2013年高考福建省理综第22题和2013年北约自主招生第12题为例，讲解等效平摆线在物理解题中的应用.

【例1】(2013年高考福建卷第22题)如图2(a)，空间存在一范围足够大的垂直于xOy平面向外的匀强磁场，磁感应强度为B．让质量为m，电荷量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度和方向入射到该磁场中．不计重力和粒子间的影响．

(1)若粒子以初速度v1沿y轴正向入射，恰好能经过x轴的A(a,0)点，求v1的大小；

(2)己知一粒子的初速度大小为v(v>v1),为使该粒子能经过A(a,0)点，其入射角θ(粒子初速度与x轴正向的夹角)有几个？并求出对应的sinθ值；

(3)如图2(b)，若在此空间再加入沿y轴正向、大小为E的匀强电场，一粒子从O点以初速度v0沿y轴正向发射，研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量vx与其所在位置的y坐标成正比，比例系数与场强大小E无关．求该粒子运动过程中的最大速度值vm．

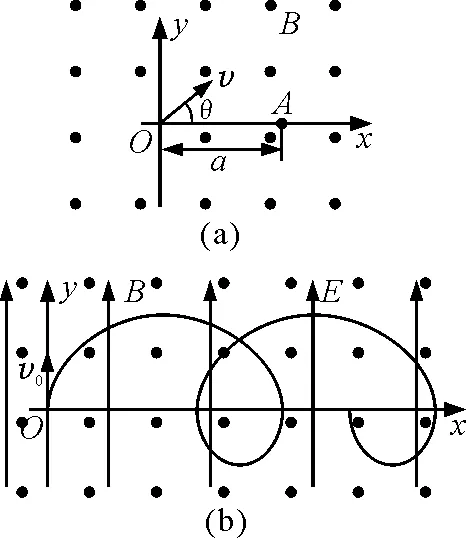
图2

标准答案给出的原解如下：

(1)带电粒子以速率v在匀强磁场B中做匀速圆周运动，半径为R，有

(1)

当粒子沿y轴正向入射，转过半个圆周至A点，该圆周半径为R1，有

(2)

将式(2)代入式(1)得

(3)

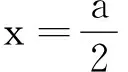
(4)

由式(1)、(4)解得

(5)

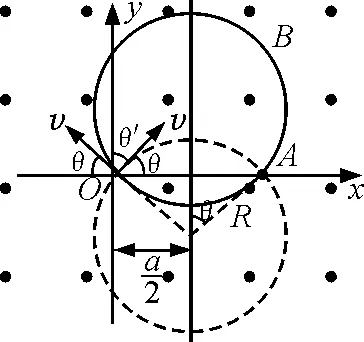
图3

(3)粒子在运动过程中仅电场力做功，因而在轨道的最高点处速率最大，用ym表示其y坐标，由

动能定理，有

(6)

由题知，有

vm=kym

(7)

若E=0时，粒子以初速度v0沿y轴正向入射，有

(8)

v0=kR0

(9)

由式(6)～(9)解得

其实第(3)问中，粒子的运动轨迹就是摆线，命题人为了降低难度，给出了“研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量vx与其所在位置的y坐标成正比，比例系数与场强大小E无关”这一条件，希望引导学生能得出正确结论．

其实，根据牛顿经典力学中力与运动的关系可知，只要物体的受力情况和初始情况确定，其以后的任一状态都是可以预知的．所以这些条件是多余的，是否正确还有待商榷．下面笔者用平摆线的等效性运动学和动力学原理解决第(3)问．

解：因为初始时x轴方向的速度为零，可等效为一个沿+x轴的匀速运动和沿-x轴的匀速运动，设其速度大小均为v2，且恰好可使qv2B=Eq，即

初始时，把沿-x轴的速度v2与v0合成，在原点O处带电粒子受力和运动分析如图4，因为沿+x轴的匀速运动的速度v2产生的洛伦兹力与电场力Eq抵消，带电粒子的受力等效成只受一个洛伦兹力qv合B作用，这个力提供向心力使粒子沿图中虚线的圆做匀速圆周运动，因此粒子的运动可看成一个以速度大小为v合的顺时针匀速圆周运动和一个以速度大小为v2的沿+x轴的匀速直线运动的合成．

图4

且

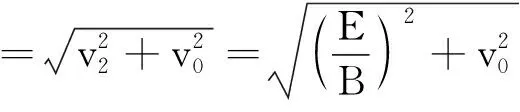
很显然当匀速圆周运动到最高点时，v合与v2同向，速度达最大值，大小为

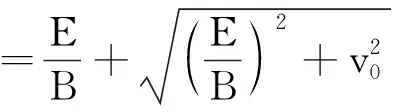
【例2】(2013北约自主招生第12题)如图5所示，在一竖直平面内有水平匀强磁场，磁感应强度B的方向垂直该竖直平面朝里．竖直平面中a，b两点在同一水平线上，两点相距l．带电荷量q>0，质量为m的质点P，以初速度v从a对准b射出．略去空气阻力，不考虑P与地面接触的可能性，设定q，m和B均为不可改取的给定量．

(1)若无论l取什么值，均可使P经直线运动通过b点，试问v应取什么值?

(2)若v为第(1)问可取值之外的任意值，则l取哪些值，可使P必定会经曲线运动通过b点?

(3)对每一个满足第(2)问要求的l值，计算各种可能的曲线运动对应的P从a到b所经过的时间．

(4)对每一个满足第(2)问要求的l值，试问P能否从a静止释放后也可以通过b点?若能，再求P在a而后运动过程中可达到的最大运动速率vmax．

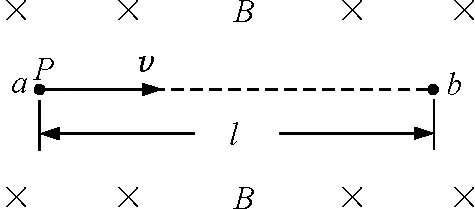
图5

解析：(1)当质点从a匀速直线运动到b时满足条件，即

mg=qv0B

得出速度

且为正电荷．

(2)这一问就是典型的平摆线运动，可将初速度v等效成为v0和v1的合成，初始时v0和v1共线(v1取正号时与v0同向，取负号时与v0反向)，可写成v=v0+v1，其初始时的受力分析和运动分析如图6(a)，只画出v1取正号时圆周运动，若v1取负号时圆周轨迹在下方，不影响解题，所以下面就以取正号分析．所以质点的运动可看成一个以速度大小为v1的匀速圆周运动和一个v0的匀速直线运动的合成．

圆周运动的周期与速度v1无关

当粒子第n次回到直线ab上时，恰好到达b点

(n=1，2，3，…)

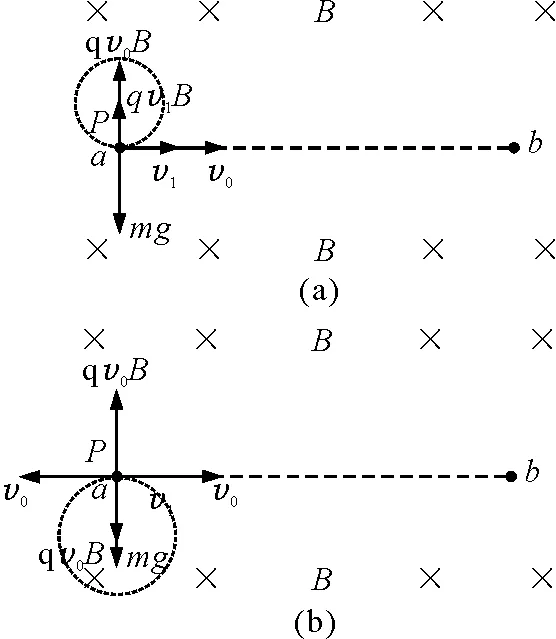
图6

(3)由(2)易知a到b的时间为

(n=1，2，3，…)

(4)解决此问与上面的方法一样，只需要把初速度为零等效一个沿ab方向的v0和与ab方向相反的-v0，质点的运动等效为一个沿ab方向的速度大小为v0的匀速直线运动和以速度大小为v0的匀速圆周运动的合成，如图6(b)所示.

圆周运动的周期与速度v0无关，仍为

当粒子第n次回到直线ab上时，恰好到达b点

(n=1，2，3，…)

所以可以通过b点．

当匀速圆周运动到最低点时，两分速度方向相同，速度最大，即

在17世纪，大批卓越的物理学家、数学家(如伽利略、帕斯卡、托里拆利、笛卡儿、费尔马、伍任、瓦里斯、惠更斯、约翰·伯努里、莱布尼兹、牛顿等等)热心于研究这一曲线的性质．所以各大考试中出现试题是历史发展的必然，在平时的教学中我们教师不要忘记物理学史，对一些历史上重要的研究方法和思维还是很有必要向学生介绍，让学生领略大师们是如何去研究复杂运动的．

在分析物体做复杂运动时，如能揭示出其运动的数学原理和客观背景，能够将物体运动规律的本质表现出来，物理情景就会更为明朗，也会使抽象的数学变得有生活意义．

参考文献

1 佘守宪,唐莹.重力场和正交均匀电磁场中的旋轮线(摆线).物理与工程，2001,11(6)

2 佘守宪,唐莹.浅析物理学中的旋轮线(摆线).大学物理，2001,20(6)

3 赵灿冬.摆线性质的物理分析方法.大学物理，2010,29(2)

4 丁明武.摆线在物理解题中的应用.中学物理，2011,29(21)

5 吴佩萱.“最速降线”问题——数学史上最激动人心的一次公开挑战.数学通报，2006,45(5)