基于棒状共晶体边界滑移的复相陶瓷开裂应力

陈诚,倪新华,张淑琴,程兆刚

（军械工程学院基础部,河北石家庄 050003）

基于棒状共晶体边界滑移的复相陶瓷开裂应力

陈诚,倪新华,张淑琴,程兆刚

（军械工程学院基础部,河北石家庄 050003）

根据共晶基复相陶瓷的组织结构特征,建立开裂应力预报模型,为分析复合材料的破坏形式提供了理论依据。共晶基复相陶瓷以含纳/微米纤维的棒状共晶体为基体,并在棒状共晶体周围分布有少量的片晶和球晶。基于棒状共晶体内纤维-基体间强约束界面所传递的拉应力,建立了载荷传递模型；根据两棒状共晶体之间或共晶体与周围其他晶粒之间的弱界面特性,通过边界滑移条件确定棒状共晶体表面切应力；考虑棒状共晶体方位的随机性,当复相陶瓷承受拉伸载荷时,借助棒状共晶体的外加应变与复相陶瓷外加载荷间的关系,得到复相陶瓷开裂应力的理论表达式,结果表明开裂应力与棒状共晶体内纳/微米纤维的直径和体积分数密切相关,复相陶瓷开裂应力随着纤维直径的增大而增大,随纤维体积分数的增大而减小。

固体力学；共晶基复相陶瓷；棒状共晶体；界面切应力；载荷传递模型；边界滑移；开裂应力

0 引言

陶瓷复合材料由于具有高强度、高硬度、高韧性以及低密度的特点,得到了广泛地应用,尤其在防弹领域[1]。共晶基复相陶瓷是以棒状共晶体为主体,并在棒状共晶体周围分布有少量的片晶和球晶,其显微结构如图1和图2所示[2]。这种复相陶瓷内有两类特殊界面：一类为两棒状共晶体之间（见图1中A处）或棒状共晶体与周围其他晶粒之间（见图1中B处）的弱约束界面,此类界面为一般晶体间的物理连接；另一类为棒状共晶体内纳/微米纤维与基体间的强约束界面（见图2）,因为t-ZrO2纳/微米纤维与α-Al2O3基体形成的共晶两相共享同一氧离子面,连接界面具有共价性质,所以两相保持强烈的化学结合。强约束界面使复相陶瓷具有高强度,而弱约束界面滑移则会提高复相陶瓷的断裂韧性。共晶基复相陶瓷的综合力学性能与两类界面的作用密切相关,因此需要通过细观力学方法确定复相陶瓷的开裂应力。

图1 共晶基复相陶瓷的显微结构Fig.1 The microstructure of eutectic composite ceramic

图2 棒状共晶体内纳/微米纤维与基体间的强约束界面Fig.2 The strong constraining interphase between nano/micron fiber and matrix in rod-shaped eutectics

复合材料的破坏是微观损伤演化过程,其力学性质与复合材料的微观结构和断裂特征密切相关。近年来,在脆性基体复合材料的力学性质和微观结构关系的研究方面取得了显著的进步,提出了新型的陶瓷基复合材料的破坏准则。例如,用Yeh-Stratton破坏准则分析了复合材料在单向拉伸载荷作用下的破坏形式,被证明是预报正交层片复合材料断裂应力的准确手段[3]。基于陶瓷基复合材料拉伸试验确定的裂纹损伤区,可以估算陶瓷基复合材料破坏时裂纹损伤区内纤维承担的应力,进而通过考虑界面性质分别建立复合材料脆性断裂和韧性断裂两类形式的强度模型[4]。这样既可以考虑裂纹的萌生与扩展,又可以考虑局部变形和界面应力分布的自然边界条件,并且获得含双线性粘性准则的无穷远集中载荷的界面剥离函数[5]。传统的剪滞模型可扩展到含微米纤维和纳米纤维的混合基体复合材料,确定基体和纤维内的局部应力,通过能量分析可预报出与相关材料参数有关的基体开裂应力[6]。上述研究表明,界面性质是决定复合材料力学性质的重要条件。为揭示共晶基复相陶瓷的破坏机理,将复相陶瓷的微观结构与宏观性能联系起来,本文根据剪滞法[7-8]确立了棒状共晶体的局部应力场,得到共晶体沿纵向的拉伸应力和共晶体表面切应力与纳/微米纤维的含量、长径比及共晶体外加应变之间的关系。考虑棒状共晶体方位的随机性,当复相陶瓷受单向拉应力作用时,计算出棒状共晶体的外加应变,进而得到复合材料的开裂应力的理论表达式。

1 棒状共晶体的界面切应力

首先研究棒状共晶体中沿纳/微米纤维方向的应力分布。从共晶体中取出一个含有纳/微米纤维的圆柱体,设纳/微米纤维直径为d0,圆柱体直径为D,圆柱体长为2L,如图3所示。

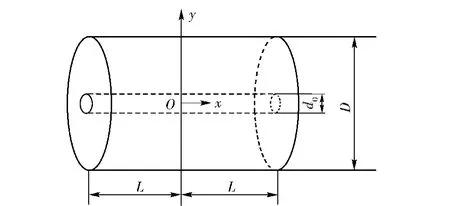
图3 棒状共晶体中的纳/微米纤维Fig.3 Nano/micron fibers in rod-shaped eutectics

设纳/微米纤维的轴向应力σn,纳/微米纤维与基体间的界面切应力为τe,因为棒状共晶体中的基体与纤维间为强约束界面,外力作用下不会出现滑移,考虑长为dx的微元,根据剪滞法可以得到平衡方程[8]为

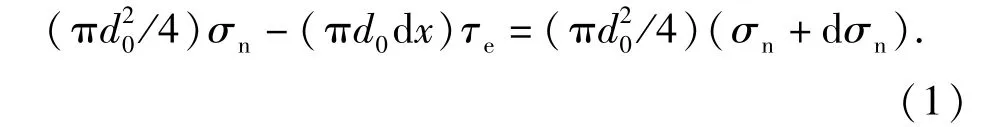
如果棒状共晶体中的基体及纳/微米纤维在外力作用下均发生弹性变形,在r=D/2处圆柱体沿x向的应变等于棒状共晶体的外加应变,并令u（x,r）为半径为r处基体沿x向的位移,τ（x,r）为相应点处的切应力。圆柱体具有轴对称性,u（x,r）及τ（x,r）不受纳/微米纤维中心轴环向角度变化的影响,根据纳/微米纤维与任一环向层r处的平衡条件可知

式中：uR及un分别为基体和纳/微米纤维的轴向位移；D/d0值与纳/微米纤维在基体中排布的微观结构有关,一般情况下,纳/微米纤维在共晶体内为近似均匀分布,可认为呈四方形排布结构,如图4所示[9]。

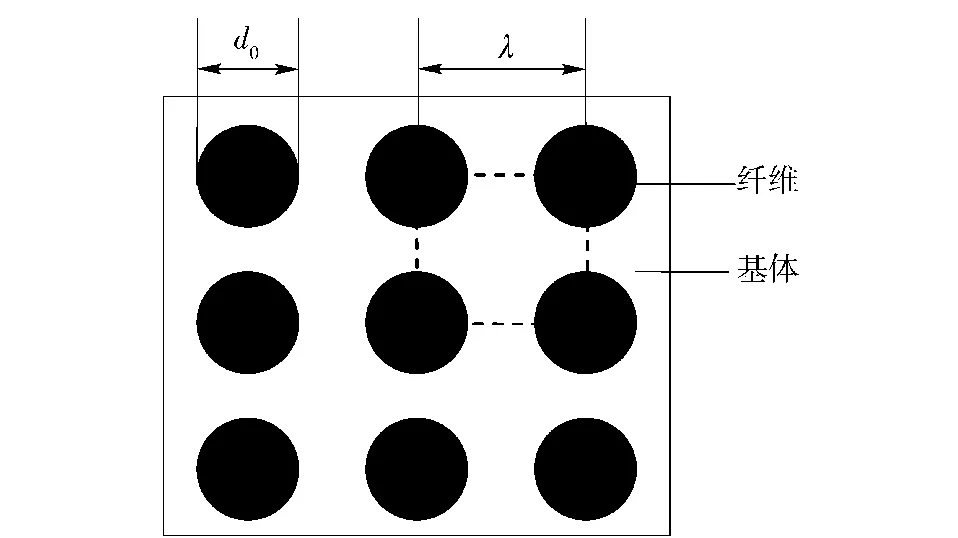
图4 纤维在基体中的排列Fig.4 The arrangement of fibers in matrix

将（13）代入（1）式中,可以求得纳/微米纤维界面处的切应力为

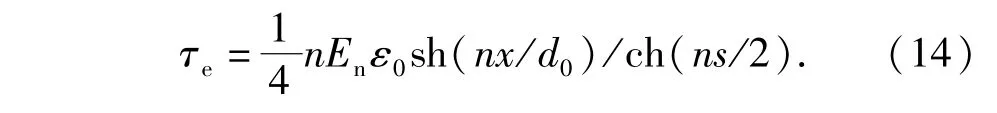
将（14）代入（2）式中,并令r=D/2,可以得到棒状共晶体外表面上的切应力

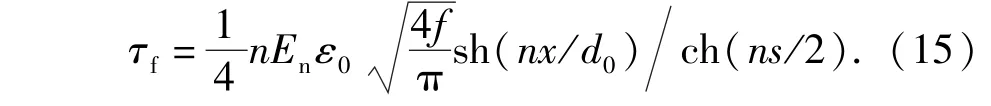
当x=L时,得到棒状共晶体外表面上的最大切应力为

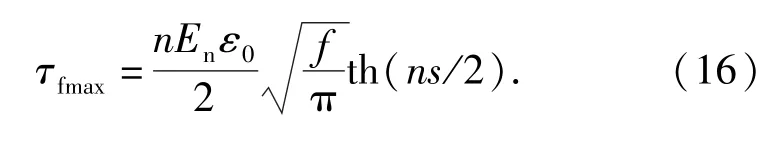
2 复相陶瓷的开裂应力

共晶基复相陶瓷主体由方位随机分布的棒状共晶体构成,复相陶瓷的开裂取决于共晶体边界的弱连接方式。如图5所示,在方位随机的某棒状共晶体周围取一无限大体。由文献[10]可知,共晶体为横观各向同性体,周围介质具有复合材料的平均性质,为各向同性体。

图5 棒状共晶体的随机方位Fig.5 The random orientation of rod-shaped eutectics

无限大体受远场应力σ作用,在共晶体处取一应力单元体,容易求出共晶体轴向的外加应变为

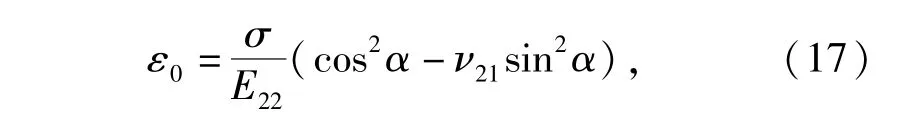
式中：E22为棒状共晶体的纵向（垂直于纳/微米纤维轴向）弹性模量；ν21为棒状共晶体的横纵泊松比,均可由文献[11]中的公式计算出来。

将（17）式代入（16）式,可得到由远场应力σ引起的棒状共晶体外表面上的最大切应力

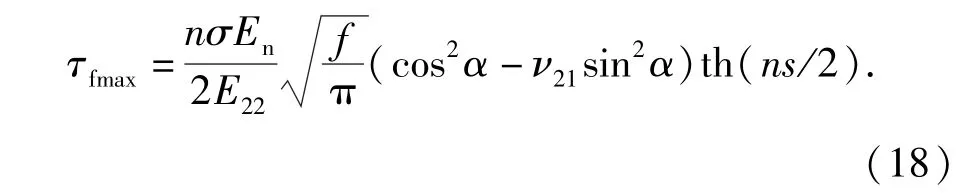
实验表明复合材料中的裂纹总是在共晶体尖端萌生[12]。当共晶体表面的切应力等于共晶体的极限应力,即τfmax=τmu时,复合材料内开始产生滑移。由文献[13]可得棒状共晶体的极限应力为

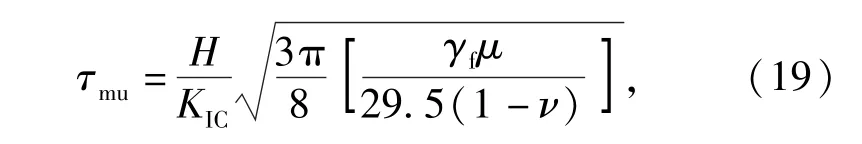
式中：γf=1.06 J/m2,为共晶体基体的断裂表面能； μ为棒状共晶体的剪切模量；ν为共晶体的泊松比,均可由文献[11]的公式计算得出；H为复相陶瓷的硬度；KIC为复相陶瓷的断裂韧性,可由实验测出[2]。

由此可得到由于棒状共晶体表面滑移引起的复合材料开裂应力为

3 结果与讨论

对于含ZrO2纳/微米纤维的Al2O3-ZrO2棒状共晶体ZrO2相变粒子的复相陶瓷,基体和纳/微米纤维的材料常数分别为Em=402 GPa,νm=0.233与En=233 GPa,νn=0.310.取纤维长度l=10 μm,由（19）式可得棒状共晶体的极限应力τmu=110 MPa.

假设纤维直径d=1 μm,开裂应力σa与纤维体积分数f的关系曲线如图6所示（当ZrO2的体积含量超过40%时,共晶体将不再是棒状结构[14]）。

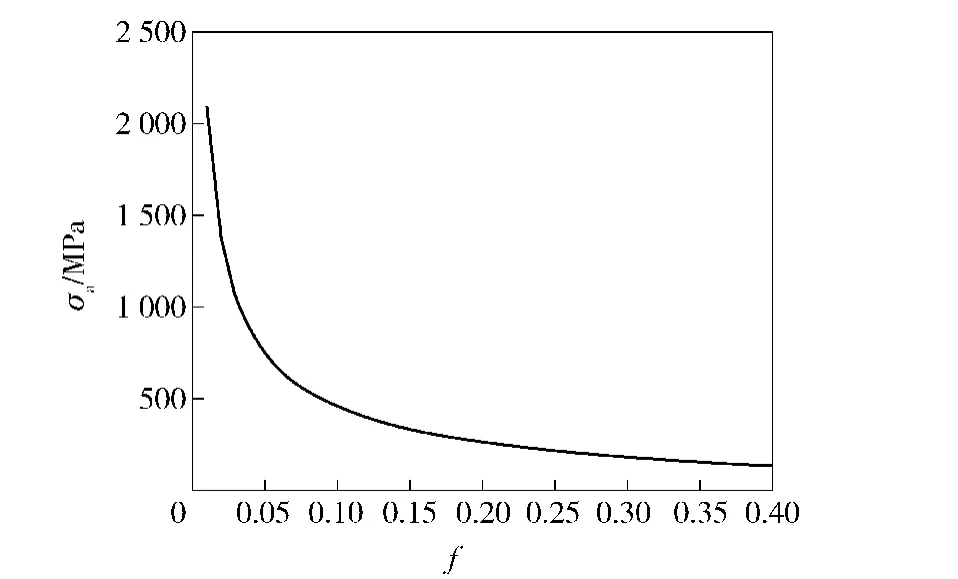
图6 开裂应力与纤维体积分数的关系Fig.6 The relationship of cracking stress and fiber volume fraction

图6显示,复相陶瓷的开裂应力随着纤维体积分数的增大而减小。当f＜0.2时,应力变化幅度较大,这是因为纤维体积分数f越小,强约束界面之间的间距就越大,强约束界面所起的作用就越小,所以弱约束界面开裂应力越大。当f＞0.3时,应力变化趋于平缓,这是因为当纤维体积分数f增大到一定程度时,强约束界面间距的变化不大,所以应力曲线趋于平缓。

假设纤维体积分数f=0.1,则复相陶瓷开裂应力σa与纤维直径d0的关系如图7所示。

图7 开裂应力与纤维直径的关系Fig.7 The relationship of cracking stress and fiber diameter

由图7可以看出,复相陶瓷的开裂应力随纤维直径的增大而增大,当纤维直径d0＜0.4 μm时,应力变化较大,这是因为纤维直径d0越大,共晶界面的间隔就越大,界面所起作用就越小,所以弱约束界面开裂应力越大；当d0＞0.5 μm时,曲线变化趋于平缓,这是因为纤维直径d0增大到一定程度时,虽然共晶界面间距变大,但共晶界面的面积变化不大,

所以应力变化趋于平缓。

4 结论

1）基于纤维-基体界面切应力所传递的棒状共晶体拉应力,建立了载荷传递模型。

2）当棒状共晶体边界滑移时,得到棒状共晶体表面切应力的表达式。结果表明共晶体表面切应力与纳/微米纤维含量、长径比以及共晶体的外加应变有关。

3）当复相陶瓷承受拉伸载荷时,基于棒状共晶体的外加应变与复相陶瓷外加载荷间的关系,得到复相陶瓷开裂应力的理论表达式。

4）通过定量计算表明,开裂应力随着纤维直径d0的增大而增大,当纤维直径d0增大到一定数值后,虽然共晶界面间距变大,但共晶界面的面积变化不大,应力曲线变化趋于平缓；开裂应力随着纤维体积分数f的增大而减小,当纤维体积分数f增大到一定数值后,由于强约束界面间距的变化不大,应力变化趋于平缓。

（References）

[1] 韩辉,李军,焦丽娟,等.陶瓷-金属复合材料在防弹领域的应用研究[J].材料导报,2007,21（2）：34-37.

HAN Hui,LI Jun,JIAO Li-juan,et al.Study on the application of ceramic-metal composite materials in bulletproof field[J].Materials Review,2007,21（2）：34-37.（in Chinese）

[2] Zhao Z M,Zhang L,Song Y G,et al.Microstructures and properties of rapidly solidified Y2O3doped Al2O3/ZrO2composites prepared by combustion synthesis[J].Scripta Materialia,2006, 55（9）：819-822.

[3] Yeh H Y,Murphy H C,Yeh H L.An examination of failure criteria for notched orthotropic ceramic matrix composite laminates[J]. Journal of Reinforced Plastics and Composites,2009,28（4）： 441-459.

[4] Yang C P,Jiao G Q,Wang B.Effects of interface properties on tensile strength of ceramic matrix composites[J].Journal of Inorganic Materials,2009,24（5）：91-92.

[5] Ou Y,Zhen Y,Li G Q.Local damage evolution of double cantilever beam specimens during crack initiation process：a natural boundary condition based method[J].Journal of Applied Mechanics,Transactions of ASME,2009,76（5）：1-8.

[6] Pavia F,Letertre A,Curtin W A.Prediction of first matrix cracking in micro/nanohybrid brittle matrix composites[J].Composites Science and Technology,2010,70（6）：916-921.

[7] Fukuda H,Chou T W.A probabilistic theory for the strength of short-fiber composites and variable fiber length and orientation[J]. J Mat Sci,1982,17（3）：1003-1008.

[8] Chon C T,Sun C T.Stress discontinuous along a short fiber in fiber reinforced plastics[J].J Mat Sci,1980,15（5）：931-937.

[9] Allen D H,Jones R H,Boyd J G.Micromechanical analysis of a continuous fiber metal matrix composite including the effects of matrix viscoplasticity and evolving damage[J].J Mech Phys Solids, 1994,42（3）：505-529.

[10] 倪新华.含界面相复合陶瓷的细观力学模型与宏观力学性能研究[D].石家庄：军械工程学院,2008.

NI Xin-hua.Research on micromechanical model and macro mechanical properties for composite ceramics with interphase[D]. Shijiazhuang：Ordnance Engineering College,2008.（in Chinese）

[11] 倪新华,刘协权,李宝峰,等.共晶界面复合陶瓷刚度的尺度效应[J].中国机械工程,2010,21（13）：1577-1581.

NI Xin-hua,LIU Xie-quan,LI Bao-feng,et al.Size dependent stiffness of eutectic composite ceramic with eutectic interphases[J]. China Mechanical Engineering,2010,21（13）：1577-1581. （in Chinese）

[12] Zhao Z M,Zhang L,Zheng J,et al.Microstructures and mechanical properties of Al2O3/ZrO2composite produced by combustion synthesis[J].Scripta Materialia,2005,53（8）：995-1000.

[13] 龚江宏.陶瓷材料断裂力学[M].北京：清华大学出版社, 2001.

GONG Jiang-hong.Fracture mechanics of ceramics[M].Beijing：Tsinghua University Press,2001.（in Chinese）

[14] Zhao Z M,Zhang L,Bai H B.Fabrication of nano-micron Al2O3-ZrO2ceramic eutectic composite from the melts by the SHS metallurgical process[J].Key Engineering Materials, Switzerland,2005,280-283：1053-1056.

Cracking Stress of Composite Ceramic Based on the Boundary Slip of Rod-shaped Eutectics

CHEN Cheng,NI Xin-hua,ZHANG Shu-qin,CHENG Zhao-gang
（Department of Basic Courses,Ordnance Engineering College,Shijiazhuang 050003,Hebei,China）

According to the organizatinal structure characteristics of eutectic composite ceramics,a prediction model of cracking stress is established,which provides theoretical foundation for analyzing the damage form of composite materials.The matrix of eutectic composite ceramics is mainly composed of rod-shaped eutectics with nano/micron fibers.A small amount of lamellar crystals and spherulites are distributed around the rod-shaped eutectics.Baesd on tensile stress transmitted by strong constraining interphase between fibers and matrix in the rod-shaped eutectics,a load-transmitting model is set up.On the basis of weak constraining interphase characteristics between rod-shaped eutectics or between rod-shaped and crystal particles around the rod-shaped eutectics,the shear stress on the surface of the rod-shaped eutectics is obtained by boundary slip conditions.Considering the random orientation of the rod-shaped eutectics,a theoretical expression of composite ceramic cracking stress is gotten based on the relationship between the applied strain of rod-shaped eutectics and the applied load of composite ceramics as the composite ceramics are subjected to tensile load.The results indicate that cracking stress is closely related to the diameter and volume fraction of nano/micron fiber.The cracking stress increases with the increase infibers diameter and decreases with the increase in fibers volume fraction.

solid mechanics；eutectic composite ceramics；rod-shaped eutectics；interfacial shear stress；load-transmitting model；boundary slip；cracking stress

O346

A

1000-1093（2014）10-1625-05

10.3969/j.issn.1000-1093.2014.10.016

2013-12-01

国家自然科学基金项目（11272355）

陈诚（1989—）,男,硕士研究生。E-mail：cc510182@126.com；倪新华（1963—）,女,教授,博士生导师。E-mail：jxxynxh@163.com