基于滑模变结构控制的移动系统滑转率控制

黄郁馨,王彤宇,林琳

（1.长春理工大学机电工程学院,吉林长春 130022；2.中国北方车辆研究所,北京 100072）

基于滑模变结构控制的移动系统滑转率控制

黄郁馨1,2,王彤宇1,林琳1

（1.长春理工大学机电工程学院,吉林长春 130022；2.中国北方车辆研究所,北京 100072）

月球车移动系统在行驶过程中其行驶参数经常发生变化,采用传统的控制方法往往不能保证在任何情况下都能得到最佳的控制效果,鲁棒性较差。滑模变结构是一类特殊的非线性控制方法,它对系统参数摄动具有很强的抑制能力,因此鲁棒性很强,并且具有算法简单易于实现等特点。根据移动系统的动力学模型及滑模变结构控制理论,建立基于滑模变结构控制的月球车移动系统滑转率控制的控制逻辑和控制算法,将其应用于月球车移动系统的滑转率控制中,并通过仿真结果分析证明该种控制方法具有较好的控制效果。分析了变结构控制系统的控制特性,为月球车滑转率控制系统的设计提供理论参考依据。

控制科学与技术；移动系统整车模型；滑转率控制；滑模变结构控制

0 引言

月球车移动系统驱动轮的过渡滑转与整车特性、车轮特性及整车行驶条件等诸多因素有关,而这些因素具有明显的非线性、时变性和不确定性[1]。传统的控制方法如PID控制,其原理简单,应用比较成熟,实现非常容易,但是PID控制的参数受被控系统的影响较大,在不同的条件下,其最优的PID参数也不相同,而月球车在行驶过程中其行驶参数将经常发生变化,这使得采用传统的控制方法往往不能保证在任何情况下都能得到最佳的控制效果,即鲁棒性较差。

滑模变结构控制是变结构控制中的一种控制策略[2]。变结构控制系统（VSS）是一类特殊的非线性控制方法,它对系统参数摄动具有很强的抑制能力[3]。这种控制方法已经应用于过程控制、机器人控制、飞机系统控制、卫星姿态控制等许多领域。

滑模变结构控制与其他控制的根本区别在于控制的不连续性,即具有使系统“结构”随时变化的开关特性。该特性可以迫使系统在一定条件下,沿规定的状态轨迹作小幅高频的上下运动,即“滑模”运动,这就使控制者与被控系统的参数变化及外部扰动无关,具有良好的鲁棒性[4-5]。但是,滑模变结构控制在本质上的不连续性将会引起系统的一种“抖振”[6]。对于一个现实的滑模变结构系统,控制力总是受到限制,从而使系统的加速度有限；另外,系统的惯性、切换开关的时间滞后以及状态检测的误差等都将会在光滑的滑动模态上叠加一个锯齿形的轨迹[7-8]。所以在实际中,抖振是必定存在的。要想从根本上完全消除抖振是不可能的,消除了抖振也就消除了滑模变结构控制的抗摄动和抗扰动能力,因此只能削弱抖振的幅度。

本文主要对月球车移动系统的滑模变结构滑转率控制进行研究,结合整车移动系统的力学模型,推导和设计滑转率控制的滑模变结构控制器,建立基于滑模变结构控制理论的控制逻辑和控制算法。根据移动系统的动力学模型和控制策略,运用Matlab/ Simulink建立系统仿真模型,进行移动系统滑转率控制的仿真计算和分析。

1 整车移动系统的动力学模型

动力学建模是为了明确月球车在确定的力或力矩作用条件下车体的运动状态,这是驱动控制设计的前提。在动力学建模过程中,要考虑车体（包括有效载荷）的质量、惯量,月球表面轮与月壤间作用力关系以及各种作用力如何计算等因素,通过经典Newton力学理论建立月球车移动系统动力学模型[9]。

图1所示,移动系统由6个具有独立驱动和转向功能的刚性车轮、3组平衡肘式悬架和3个铰接承载机构组成,构成新型的平衡-铰接复合式移动构型。该方案将6个刚性车轮分布排列在探测器两侧,左右轮对称布置,保障均匀的车轮静态载荷；后两轮形成横向平衡肘式悬架,前4轮双侧形成纵向平衡肘式悬架对称布置在仪器舱两侧,全部悬架均采用4连杆式平衡肘悬架,以保障复杂地面环境下动态行驶过程中车轮载荷的垂直分布。

图1 月球车移动系统模型Fig.1 Model of lunar rover locomotion system

月球车着陆点一般选在较为平坦的月面上,因此,建立月球车在平坦地形的运动学模型。月球车在平坦地形运动时,由于俯仰、翻滚等运动变化较小,在实际控制中可将其简化为近似平面运动模型。平面运动时,月球车有其固有的运动特性,可将平面运动轨迹转换为直线运动、绕半径转弯和原地差速转弯几种模式[10]。本文主要针对直线运动进行分析,故做如下假设：1）所有车轮均视为刚性车轮且各车轮质量特性和几何尺寸完全相同；2）月球车直线前行,不考虑横向运动；3）车体结构对称,只考虑1/2车体模型；4）月球车近似在水平平面内运动,各车轮轮心的纵向速度近似等于车体质心的纵向速度；5）不考虑由于车身的侧倾而引起的同轴左右车轮之间的载荷转移；6）不考虑行驶过程中车身的俯仰和侧倾运动。

移动系统1/2模型的受力分析图可简化为图2所示,Fn表示地面对车轮的法向支撑力,T1、T2、T3分别表示驱动电机施加在各车轮上的驱动转矩,G表示月球车移动系统的重量,v为月球车的行驶速度。Fdp表示驱动车轮所产生的挂钩牵引力,其定义为土壤推力减去土壤阻力,即

式中：Ft表示土壤对车轮的推力；Fr为土壤对车轮的阻力,包含刚性车轮压实土壤所产生的压实阻力Frc与驱动轮由于滑转所产生的附加滚动阻力Frs.

根据贝克公式推导可得

图2 1/2月球车移动系统对称模型受力分析图Fig.2 1/2 force analysis of symmetric model of lunar rover locomotion system

式中：c为土壤内聚力；b为轮宽；l为车轮接地面积长度；W为车体施加给车轮的垂直载荷；φ为土壤内摩擦角；kx为土壤在x轴方向上的剪切变形模量；s表示车轮滑转率。刚性车轮压实阻力,可作为沉陷量的函数[9]表示为式中：z0为车轮垂直载荷引起的车轮静态下陷量；n为土壤的沉陷指数；K为土壤变形模量。

Frs随车轮滑转率的增加而增大,当车轮的滑转率0≤s＜1时,其近似计算公式为[8]式中：Fp为车轮的圆周力,等于驱动轮上的作用力矩除以车轮半径r.

而当车轮滑转率为1,即车轮空转情况下,此时车速为0,滑转产生的滚动阻力与压实阻力的和将与土壤推力一致,使地面作用在车体上的合力为0,避免在计算中发生车速为负值的情形,即滑转产生的滚动阻力计算公式应为

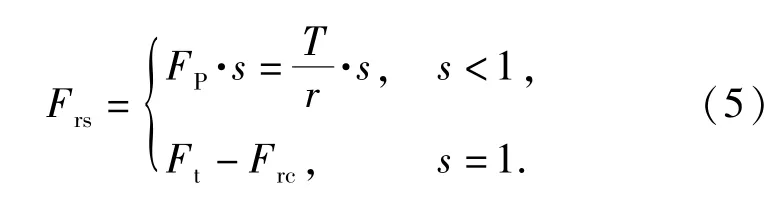
由受力分析得出月球车移动系统1/2模型直线行驶的动力学方程为

式中：m=m′/2,m′为月球车移动系统的质量；si为各车轮的滑转率；Iwi表示各个车轮的转动惯量；Tti、Tri、Trci表示各个车轮所受到的各种力矩。

由于si是v和ωi的非线性函数,因此上述动力学方程是一组非线性耦合方程。根据滑转率的定义

又由各车轮所受的土壤推力Fti、土壤阻力Fri和阻力矩Tri都是滑转率si的函数,因此可将（11）式整理成月球车移动系统滑转率控制的控制模型

2 滑模变结构控制在月球车移动系统中的应用

根据建立的月球车移动系统的动力学模型可以看出,月球车动力学模型中存在难以准确获知的月面环境参量,如土壤的粘聚模量kc、土壤的摩擦模量kφ、内聚力系数c、内摩擦角φ等,因此月球车动力学方程（12）式中的函数f（x,v）和B（x,v）均是不能精确已知的非线性函数,对于这样的存在参数不确定性的非线性系统,采用滑模变结构控制是一种简便有效的方法。

在实现月球车移动系统滑转率的滑模变结构控制时,将滑转率s作为控制目标,设控制目标即理想滑转率为sa,则误差e=s-sa,那么滑模变结构控制月球车移动系统驱动轮的滑转实质上就是调节驱动轮的实际纵向滑转率与目标滑转率的差值,并使之趋于0.选取切换函数为

式中：C为待定系数,C＞0.

如果以纵向滑转率s和其导数构成一个相平面,则切换线是斜率为-C,且过点（sa,0）的直线。变结构控制的目标就是选取合适的控制变量,使月球车在驱动过程中,按一定的控制规律使其相轨迹（s,s·）能够沿切换线滑向控制目标（sa,0）.

根据定义,驱动时车轮的滑转率

通过（13）式～（17）式可以看出,如果将各式代入进行求解,将使不等式变得非常复杂,分析非常困难,而且可能得不出应有的结果。采用趋近率控制满足广义滑模条件,而且是一个等式,只要确定合适的参数就很容易设计出变结构控制器。下面采用指数趋近率控制进行控制器设计。

1）当m（s）＞0时,

式中：ε为等速趋近律,ε＞ 0；k为指数趋近阶次, k＞0.

同理可以得到

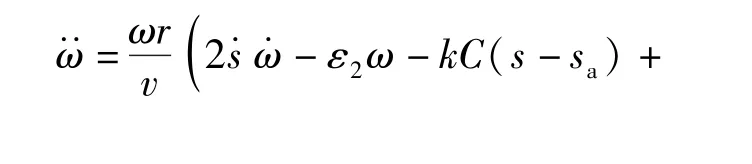
3 滑模变结构控制的月球车滑转率控制系统仿真分析

3.1 仿真结果分析

建立基于滑模变结构控制理论的指数趋近控制规律下的月球车移动系统滑转率控制的控制逻辑与算法,结合月球车移动系统动力学模型,采用Matlab/Simulink软件建立月球车滑转率控制系统的Simulink仿真模型,并对其仿真结果进行分析。仿真的流程图如图3所示。滑膜变结构控制系统仿真模型和PID控制系统仿真模型如图4、图5所示。

图3 滑转率控制仿真流程框图Fig.3 Simulation flow diagram of slip ratio control

图4 VVS控制系统仿真模型Fig.4 Simulation model of VVS control system

基于滑模变结构控制的月球车滑转率控制系统仿真分析,设定控制器参数为：C=15,ε=10, k=5.球车移动系统的相关参数为：m=m′/2= 60 kg；单轮的转动惯量Iw1=Iw2=Iw3=0.06 kg·m2；仿真中所采用的模拟月壤特性参数为：q0= 0.037 5,kx=0.036 m,c=800 N/m2,φ=37.2°,n= 1.0,kc=1.37 kN/mn+1,kφ=814 kN/mn+2,g= 1.633 33 m/s2.根据样车的轮壤通过性试验得出,驱动轮的纵向滑转率理想值控制在0.3左右时,能够既防止驱动轮过度滑转,又使驱动轮获得最大的驱动效率[11]。仿真计算结果如图6～图11所示。

由图6可以看到,VVS控制状态下,将滑转率控制在理想值sa=0.3附近时,控制的响应很快,控制过程也很平稳。而PID控制状态下,月球车驱动轮发生过度滑转,其滑转率接近为1.

图7为驱动转矩的控制曲线,在车轮发生滑转的情况下,输出转矩由4.5 N·m降低到约2.8 N·m,从而抑制了车轮的过度滑转并使滑转率保持在理想值。同时,仿真结果也表明,通过采用趋近率控制方法使“抖振”的影响得到了削弱,由控制转矩的开关切换所产生的“抖振”现象对控制结果的影响并不明显。

图8是车轮的旋转角速度控制曲线,从图8可以看出,VVS控制状态下,角速度上升的趋势得到抑制,有效避免了车轮发生高速空转的情况。

图5 PID控制系统仿真模型Fig.5 Simulation model of PID control system

图6 车轮滑转率控制曲线Fig.6 Control curves of wheel slip ratio

图9为车速的控制曲线,由图9可以看出,PID控制状态下车速仅相当于VVS控制状态下车速的约50%,驱动轮上所施加的驱动转矩也较PID控制时的驱动转矩大大降低,可见当采取滑模变结构控制滑转率时,月球车的驱动效率大大得到了提高。

图10是车轮沉陷量的控制曲线,由图10可以看出,VVS控制状态下各车轮的沉陷量得到了抑制并较快地趋于稳定值,避免了车轮的过度滑转下陷。

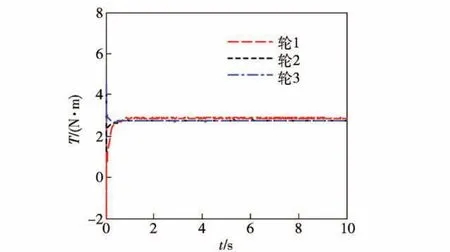
图7 驱动轮驱动力矩控制曲线Fig.7 Control curves of driving torque for each drive-wheel

图11为滑模变结构控制的相轨迹图,正如前面的分析,在控制过程中,其相轨迹（s,ds）将迅速趋于切换线,并在到达切换线之后将沿切换线快速滑向设定的理想值（sa,0）,从而达到控制的要求。

3.2 主要参数对控制性能的影响

滑模变结构控制器中参数较多,分析变结构控制器中主要参数对控制性能的影响。

3.2.1 切换面参数值C的影响

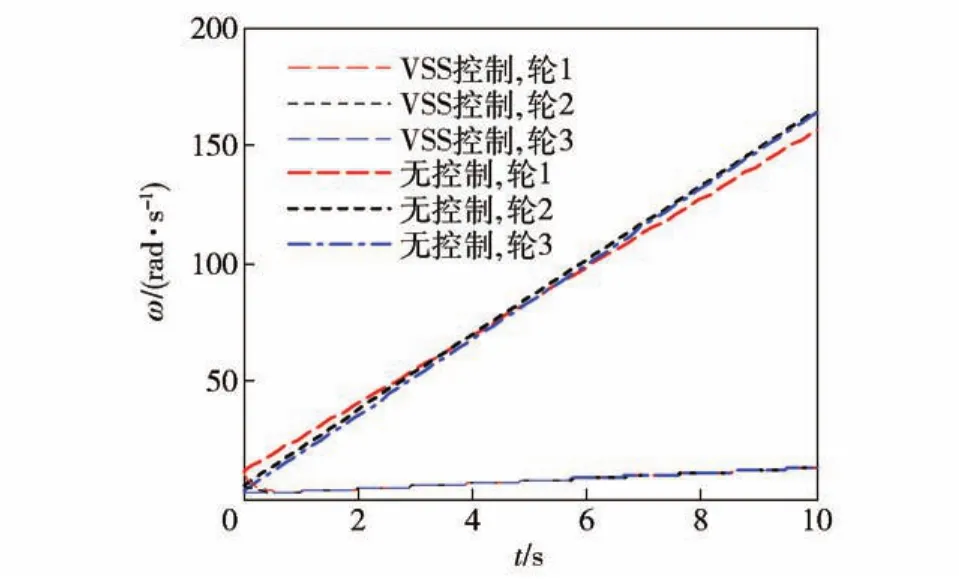
图8 车轮旋转角速度控制曲线Fig.8 Control curves of wheel rotation angular velocity

图9 整车速度控制曲线Fig.9 Control curves of vehicle speed

图10 车轮沉陷量控制曲线Fig.10 Control curves of wheel subsidence

参数C值表示切换线的负斜率,不同的C表示不同的切换线,系统的相轨迹将沿不同的切换线滑向目标值,而对其控制效果基本无多大影响。取C值分别为5和15,对两种情况进行仿真,其余各参数相同。仿真结果如图12、图13所示。

从相轨迹比较图13不难看出,随着C的改变其切换线的斜率也将随之改变,从而改变相轨迹的形状,但当运动点到达切换线后都将沿着切换线滑向目标值（sa,0）,所以对其控制效果无多大改变,这一点可以从图13滑转率的控制曲线上明显地看出。

3.2.2 等速趋近率ε的影响

图11 变结构控制相轨迹和切换线Fig.11 Phase locus and switching line of variable structure control

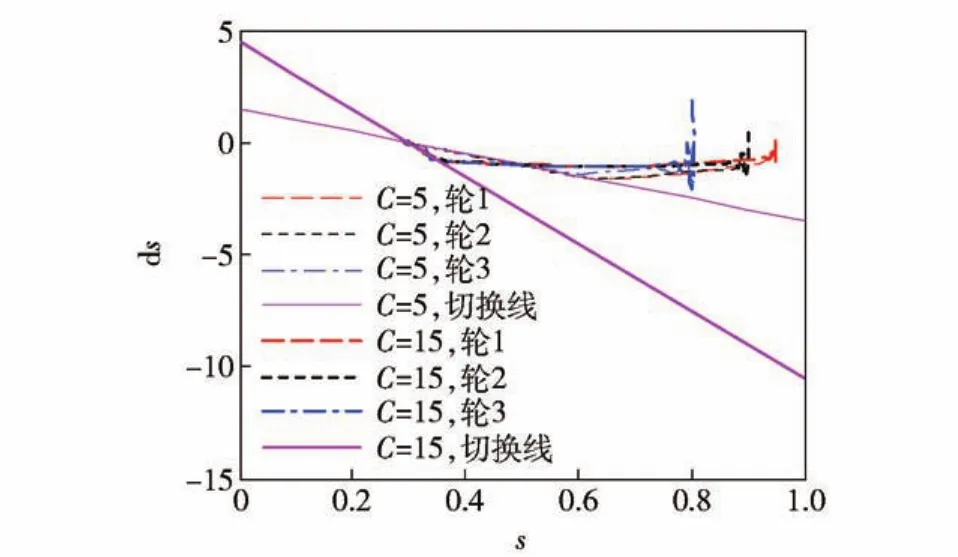
图12 相轨迹与切换线Fig.12 Phase locus and switching line

图13 驱动轮的滑转率控制曲线Fig.13 Control curves of driving wheel slip ratio

等速趋近率ε表示系统的运动点趋近切换线m（s）=0的速率,ε小,趋近速度慢,ε大,趋近速度快。ε被称为趋近速率常数。图14、图15为对ε两种情况的仿真结果,ε分别对应1和10两种情况,其余各参数相同。

从上面的仿真结果可以看出,ε的变化会改变相轨迹的路线,当ε较大时,运动点可以较快的到达切换线并沿切换线滑向控制目标,而较小时,运动点需经过一段较长的运动才到达切换线,然后沿切换线滑向控制目标,尽管最终都到达控制目标,但较大ε肯定要比较小ε先达到控制目标,从而获得更好的控制性能。从图13的滑转率控制曲线图可以比较明显地看出它们在控制效果上的差别。根据系统的实际结构和控制要求,选择合适的ε对于加快系统的响应速度,提高控制系统的性能具有重要的作用。

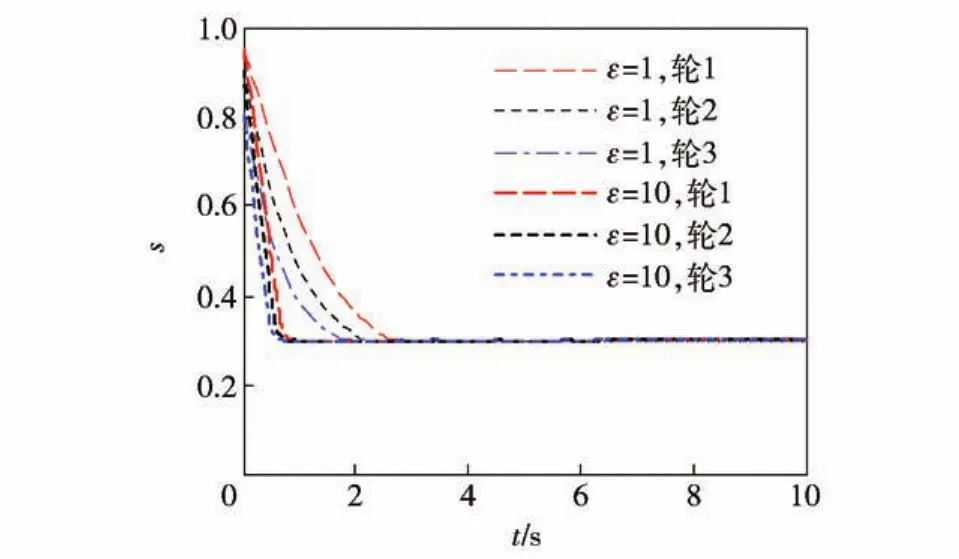
图14 驱动轮的滑转率控制曲线Fig.14 Control curves of driving wheel slip ratio

图15 相轨迹与切换线Fig.15 Phase locus and switching line

3.2.3 指数趋近阶次k的影响

分别对k=0（等速趋近率控制）和k=15（指数趋近率控制）两种情况进行了仿真,其余参数均相同。图16、图17分别表示两种情况的仿真结果。

图16 相轨迹与切换线Fig.16 Phase locus and switching line

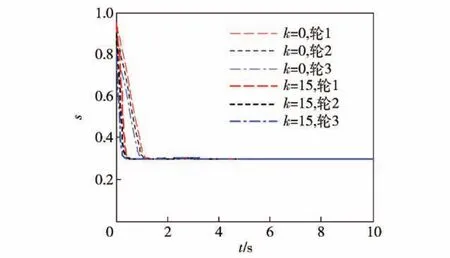
图17 驱动轮的滑转率控制曲线Fig.17 Control curves of driving wheel slip ratio

从上面的仿真结果不难看出,k值的变化能够改变系统的趋近速度,一般来说,趋近速度是随着k的增大而加快,它只影响系统到达切换线之前的运动轨迹,即改变系统的动态品质,到达切换线之后都是沿切换线的滑动,这也是采用趋近率控制的主要作用。从图17的滑转率控制曲线可以看出二者的差别比较小,说明采用两种趋近率控制时对其控制效果影响较小。

3.2.4 土壤参数对滑模控制滑转率的影响

月球车在不同的路面上行驶,要求滑转率控制系统具有一定的路面适应能力,为此在不改变控制器各参数的条件下,改变土壤的特性参数,进行仿真计算,取新的土壤参数为：q0=0.028,kx=0.014 3 m, c=900 N/m2,φ=35.6°,n=1.0,kc=3 325 N/mn+1,kφ= 339 810 N/mn+2,g=1.633 33 m/s2.控制器的参数仍然设为：C=15,ε=10,k=5.理想滑转率仍设定为0.3.图18、图19为其仿真结果。

图18 驱动轮的滑转率控制曲线Fig.18 Control curves of driving wheel slip ratio

图18为其滑转率控制曲线,车轮的滑转率仍然很好地被控制在目标值附近,非常平稳,与先前土壤参数条件下的控制效果无多大的变化。图19的相轨迹图也与先前没有多大的变化,这说明土壤参数对滑模控制滑转率的控制性能影响非常小,滑膜变结构控制具有很好的鲁棒性。

图19 相轨迹与切换线Fig.19 Phase locus and switching line

4 结论

1）建立了月球车移动系统的动力学模型。建模过程采用轮式移动机器人的动力学建模的常用经典力学方法,忽略了车体的侧向运动及沿垂直月面方向上的位移,以各驱动轮的驱动力矩作为输入,考虑车轮纵向的滑移,给出月球车移动系统的动力学模型。

2）建立月球车移动系统滑转率控制的控制策略。建立指数趋近滑模控制规律下的控制算法。滑模变结构控制方法是一类特殊的非线性控制方法,它对外部干扰具有良好的鲁棒性,它根据月球车行驶过程的状态变量来确定要控制的驱动力矩。

3）对基于滑模变结构控制的月球车滑转率控制系统进行了仿真分析。从仿真分析中可以看到：建立的基于滑模变结构控制的月球车滑转率控制逻辑与算法是正确的。通过对滑转率进行控制,能够有效提高整车的驱动效率,改善移动系统的牵引性能,有效避免车轮的过度滑转下陷,提高整车的安全性能,且具有很好的路面适应能力,鲁棒性强。

（References）

[1] Richter L,Ellery A,Gao Y,et al.A predictive wheel-soil interaction model for planetary rovers validated in test beds and against MER mars rover performance data[C]∥10th European Conference of the International Society for Terrain-Vehicle Systems.Budapest,Hungary：ISTVS,2006.

[2] 谷侃锋,王洪光,赵明扬.滑转率对月球车车轮驱动力学特性的影响分析[J].计算机仿真,2008,25（6）：25-29.

GU Kan-feng,WANG Hong-guang,ZHAO Ming-yang.Influence of wheel slip on the dynamic characteristic of lunar rover wheels[J]. Computer Simulation,2008,25（6）：25-29.（in Chinese）

[3] 郭凌龙.液压系统滑模变结构控制特性分析[J].山西科技, 2012,27（5）：84-87.

GUO Ling-long.Analysis on the characteristics of the control of the sliding mode variable structures of hydraulic systems[J].Shanxi Science and Technology,2012,27（5）：84-87.（in Chinese）

[4] 赵旖旎.灵长类仿生机器人悬臂运动仿生与控制策略研究[D].哈尔滨：哈尔滨工业大学,2010.

ZHAO Yi-ni.Bio-brachiate and brachiation control of bio-primates robot[D].Harbin：Harbin Institute of Technology,2010.（in Chinese）

[5] 胥红星,孔昭毅.一个混沌系统的自适应滑模变结构控制[J].重庆工商大学学报：自然科学版,2012,29（9）：29-33.

XU Hong-xing,KONG Zhao-yi.Adaptive sliding mode variable structure control of a chaotic system[J].Journal of Chongqing Technology and Business University：Natural Science Edition, 2012,29（9）：29-33.（in Chinese）

[6] 王长旭,孟中,韩松伟.基于卡尔曼滤波滑模控制的伺服系统设计仿真[J].光电工程,2010,37（2）：22-26.

WANG Chang-xu,MENG Zhong,HAN Song-wei.Design and simulation of servo system based on Kalman filtering sliding mode control [J].Opto-Electronic Engineering,2010,37（2）：22-26.（in Chinese）

[7] 唐国元,宾鸿赞.ABS的模糊滑模变结构控制方法及仿真研究[J].中国机械工程,2007,18（13）：1629-1632.

TANG Guo-yuan,BIN Hong-zan.Simulation study on fuzzy sliding mode control approach for ABS[J].China Mechanical Engineering,2007,18（13）：1629-1632.（in Chinese）

[8] 王其东,章贵华,陈无畏.基于滑模变结构控制的车辆动力学稳定性控制研究[J].中国机械工程,2009,20（5）：622-626.

WANG Qi-dong,ZHANG Gui-hua,CHEN Wu-wei.A study of vehicle dynamics stability control based on variable structure control[J]. China Mechanical Engineering,2009,20（5）：622-626.（in Chinese）

[9] 焦震.基于地面力学的月球车动力学建模与仿真研究[D].哈尔滨：哈尔滨工业大学,2009.

JIAO Zhen.Dynamics modelling and（ADAMS）simulation for lunar rover based on terramechanics[D].Harbin：Harbin Institute of Technology,2009.（in Chinese）

[10] 院老虎.六轮非对称月球车运动控制方法及参数辨识研究[D].哈尔滨：哈尔滨工业大学,2010.

YUAN Lao-hu.Research on motion control methods for asymmetric structural lunar rover with six wheels and its parameters identification[D].Harbin：Harbin Institute of Technology,2010.（in Chinese）

[11] 唐正义,吕振华,赵建新,等.月球车驱动轮在模拟月壤上的沉陷特性实验分析[J].航天器环境工程,2012,29（1）： 371-376.

TANG Zheng-yi,LYU Zhen-hua,ZHAO Jian-xin,et al.Analysis of sinkage of rigid driving wheel rolling on simulant lunar soil[J]. Spacecraft Environment Engineering,2012,29（1）：371-376. （in Chinese）

Slip Ratio Control of Locomotion System Based on Sliding Mode Variable Structure Control

HUANG Yu-xin1,2,WANG Tong-yu1,LIN Lin1
（1.College of Mechanical and Electric Engineering,Changchun University of Science and Technology,Changchun 130022,Jilin,China； 2.China North Vehicle Research Institute,Beijing 100072,China）

The running parameters of lunar rover locomotion system often varies during running.The traditional control method cannot be used to gain the optimal control effect in any case.The variable structure control with sliding mode（VSS）is a special non-linear control method and has strong robustness. The method is easy to be realized.The control logic and algorithm of lunar rover slip-ratio control are established based on the dynamic model of lunar rover and the variable structure control system with sliding mode theory.The control characteristics of VSS are analyzed in details.VSS is applied in slip-ratio control of the lunar rover locomotion system successfully.The simulation is conducted.The simulation results show that the control method has good control effect.

control science and technology；lunar rover locomotion system model；slip-ratio control；variable structure control with sliding mode

TP275

A

1000-1093（2014）10-1707-09

10.3969/j.issn.1000-1093.2014.10.027

2013-05-28

黄郁馨（1973—）,男,研究员级高级工程师。E-mail：huangyuxin5000@163.com；王彤宇（1970—）,男,教授,博士生导师。E-mail：wangtongyu@edu.com.cn