考虑休息的维修任务调度模型及其求解算法

吕学志,陈乐,尹健,范保新

(1.总参谋部炮兵训练基地模拟训练中心,河北宣化 075100;2.装备学院指挥与管理系,北京 101400)

考虑休息的维修任务调度模型及其求解算法

吕学志1,陈乐2,尹健1,范保新1

(1.总参谋部炮兵训练基地模拟训练中心,河北宣化 075100;2.装备学院指挥与管理系,北京 101400)

由于维修资源通常具有使用周期性,即每工作一段时间需要进行休息,而维修任务具有紧迫性,需要不间断地进行,如何在给出维修任务调度方案的同时也给出维修资源的休息时间是一个值得探讨的问题。文中给出考虑休息的维修任务调度问题的假设条件,并建立了一种混合整数规划模型,对问题进行了数学描述。提出一种粒子群求解算法,包括算法框架、粒子表示、资源技能分配算法、粒子解码过程、更新公式等。通过具体实例,证明了模型与算法的有效性。

兵器科学与技术；维修资源；维修任务；调度；粒子群优化算法

0 引言

装备是遂行一切军事行动的物质基础,装备维修保障活动是军事行动不可或缺的重要组成部分,维修保障活动的好坏直接影响着军事行动的成败。维修任务调度问题是装备保障活动中的一个重要决策问题,其主要目的是确定维修任务起始时间、所需维修资源,该问题解决的好坏决定了维修的执行效率。

国内外许多研究人员对维修任务调度问题进行了研究,对维修任务调度问题的构成要素、决策目标、问题本质有了深刻认识,建立了多种维修任务调度模型,并给出了模型的求解算法,具有一定的实践指导意义。国内学者建立了许多独立的规划模型,并使用了启发算法、智能算法对其进行求解,但并未将其与项目调度问题结合起来。王正元等[1]以尽快恢复参战作战单元的战斗力为目标,提出了一种考虑维修专业的动态维修任务调度的优化方法。文献[2-3]分别建立了基于最大保障时间的维修任务调度模型以及考虑维修流程的多单元维修任务调度模型,并给出了启发算法。

国外学者多将维修任务调度问题看作项目调度问题,这一点需要我们借鉴。文献[4]将基地级维修任务抽象为大规模复杂的项目调度问题,研究了在资源约束下与随机工期情况下军用飞机基地级维修任务调度的新方法。

资源约束项目调度问题(RCPSP)研究从时间和资源上合理安排调度项目的活动,在资源最优利用的同时实现既定目标的最优化[5]。根据资源、活动、执行模式和目标函数等4种属性可以对RCPSP进行分类,不同类型的组合又形成不同的RCPSP[6]。在项目调度问题中,资源通常具有一定的柔性,即具有多种能力。而能力指完成某项任务所需的技能或功能,对于人力资源指技能,对于机器设备等则指功能。例如,维修人员具有焊接和喷漆技能;机器具有弯板和切割功能。国外学者在维修任务调度问题研究中,考虑到了维修资源的柔性。例如,法国的Bellenguez等[7-8]对多技能员工约束项目调度问题(MSPSP)进行了深入的研究。MSPSP可以看成是传统RCPSP的一个推广。在文献[7-8]所建的模型中:假设技能具有一定级别区分,例如程序员可以分为初级、中级、高级;员工具有一定的不可用期,也就是说员工休假的时候不能被分配来执行任何活动。文献[7-8]给出了一种基于优先表的禁忌搜索算法和两种遗传算法,还将研究成果应用于维修任务调度。

国内学者也开始对柔性资源约束项目调度问题(FRCPSP)进行研究,但没有将其应用于维修任务调度问题中。喻小光等[9]提出了柔性资源约束的资源水平项目调度问题,建立了问题的数学模型,设计了基于改进串行调度生成模式和网络最大流柔性资源分配模型的路径重连算法。黄敏镁等[10]针对解决具有柔性资源约束的产品开发项目调度问题,以遗传算法和最大流理论为基础,提出了问题求解的改进遗传算法。

在军用装备维修时,维修资源通常还具有周期性,例如,维修人员(维修设备)需要每工作一定时间必须休息一段时间,而目前的维修任务研究中还没有考虑到维修资源的使用周期,在给出维修任务调度方案的同时并不能够给出维修资源的休息时间。本文将给出了一种考虑休息的维修任务调度优化模型及其求解算法。

1 数学模型

考虑休息的维修任务调度优化模型可以描述为:

1)整个维修任务的结构可以用一张活动节点图G=(J,Q)表示,G中节点J表示维修任务集合, Q表示维修任务之间的关系;|J|表示维修任务集合J中维修任务的数量;维修任务之间存在着由于技术等要求产生的时序约束,记Pj为任务j的紧前任务集合;定义任务1和任务|J|是唯一最早开始和最晚结束的任务且均为虚任务,它们不消耗资源并且执行时间为0,分别称为源任务和收尾任务;非虚任务数为|J|-2;维修任务j的工期为dj.

2)C表示与维修任务执行相关的全部技能集合,|C|表示技能集合C中技能的数量;对于维修任务的每项维修任务而言,其对资源的技能需求是不同的,即维修任务j需要一组技能Cj,Cj∈C;维修任务与技能的关系也可以用任务-技能矩阵MJ来表示这种关系,其中矩阵元素m表示维修任务j对技能c的需求量。

3)R表示维修资源集合,|R|表示维修资源集合R中资源的数量;本文中的维修资源属于柔性资源,具有柔性。柔性资源是指可以应用于一种以上的不同场合的可更新资源;柔性是资源具备多种技能的属性,可用资源-技能矩阵MR表示,定义MR=其中m表示资源r具备技能c的水平,m∈{0,1},r∈R,c∈C;若m=l,资源r完全具备技能c,l为时间段的下标(l∈L={1,…,|L|}),其中|L|为调度时间范围内时间段的数量。|L|= ceil(T|J|/λ),T|J|为整个维修任务的期限,单位为h, ceil()是向上取整函数,如ceil(2.2)=3;若m=0,资源r完全不具备技能c;资源在资源-技能矩阵的限定下执行维修任务。

4)维修资源除了具有柔性之外,还具有使用周期性。人员必须每λ小时休息τ小时。

5)进一步做以下假设:A1维修任务执行期间不允许中断;A2只有同时具备技能组合Cj时,维修任务j才能开始;A3在任一时刻维修人员至多能使用一项技能,也就是说每个维修人员被认为是一元资源;A4维修资源的休息时间也不允许中断;A5维修任务的工期不能超过每个时间段最长工作时间。

6)问题的解是确定维修任务与休息的开始时间及资源-技能分配方案。

目标(1)式表示最小化维修任务最终完成时间。约束(2)式表示按照维修任务对技能的要求(即每个维修任务的每种技能所需的人员)来分配维修人员;根据假设A2、A3,为了防止维修人员使用不同技能执行同一个维修任务,约束(3)式限定了每个维修人员在每项维修任务中最多使用一种技能。约束(4)式表示如果维修任务j是维修任务j′的紧前任务,则维修任务j在j′开始之前完成。约束(5)式和(6)式限制了每个休息时间段的时间范围,根据假设A4维修资源的休息时间也不允许中断。约束(7)式限定了Yjj′,其中Δ是无穷大的数,表示如果Yjj′=1,即j在j′之前完成,则j′的开始时间至少要比j的开始时间迟dj,如果Yjj′=0,恒成立;根据假设A3中的一元资源假设。约束(8)式与(9)式分别限定了、.约束(10)式与(11)式限定了维修任务与休息时间的序列。约束(12)式根据假设A5限定了维修任务的工期不能超过每个时间段最长工作时间。约束(13)式与(14)式表示对变量的约束。

2 求解算法

本文提出的维修任务调度问题是标准FRCPSP的一种变形,同时也是经典RCPSP的一个特例和拓展。FRCPSP是一个更为一般化的单模式RCPSP,与多模式RCPSP(MRCPSP)相似,这是因为任务可以通过多种模式进行,每种模式中资源的组成不同。但是,MRCPSP仅仅描述了通过时间与资源权衡来执行任务,并不能体现资源的柔性,这也是FRCPSP与MRCPSP的本质区别。随着任务技能需求与人员技能数量的增加,FRCPSP中的模式数量将急速增长。

相比较典型的资源约束项目调度模型,本文提出的维修任务调度模型更加复杂:一是由于维修资源具有柔性,存在任务-技能-资源的两层映射,需要考虑资源-技能分配问题;二是由于需要考虑维修资源的休息时间,在安排维修任务起始时间的同时要给出维修资源的休息时间;三是维修时间的安排也会影响到资源的分配。所以,由于经典RCPSP是NP-hard问题,本文提出的维修任务调度问题是其更为一般化的形式,所以本文提出的维修任务调度问题也是NP-hard问题。

智能算法是求解NP-hard问题的有效方法。粒子群优化(PSO)算法已经应用于经典RCPSP的求解,并且取得很好的效果[11-12]。所以,下文将提出一种基于PSO算法的求解算法。

2.1 算法框架

PSO算法框架为:

1)产生初始粒子群。评价初始粒子群粒子,确定粒子的个体极值pi、全局最优pg;

2)迭代次数加1,对粒子进行更新;

3)对整个种群进行评价,确定粒子的个体极值pi和整个种群中的全局最优pg;

4)判断是否满足算法结束条件,若是则转步骤5,否则转步骤2;

5)利用已知全局最优解生成项目(维修任务)调度计划(包括维修任务的开始时间、维修人员在每个时间段的休息开始时间,资源-技能分配方案),算法结束。

2.2 粒子表示与初始化

算法采用基于任务序列的粒子表示方法。粒子所表示的任务序列对应一个先序可行的任务序列,任务在序列中的位置表示任务调度的优先顺序。粒子维数为维修任务的总数,即D=|J|,粒子适应值对应其生成调度的工期。如粒子xi=(xi1,…,xij,…,xi|J|),前|J|个分量对应于任务xij,j∈J,任务xij在粒子转化为调度方案时,其调度次序为j,粒子的适应值对应其生成调度的工期。图1是调度问题实例的网络结构图,任务1是虚拟开始任务,任务13是虚拟结束任务,该项目的一个可行粒子为x1= (1,2,3,4,10,8,5,6,11,7,9,12,13).

图1 项目调度问题的例子Fig.1 Example of project scheduling

2.3 基于优先规则的柔性资源-技能分配算法

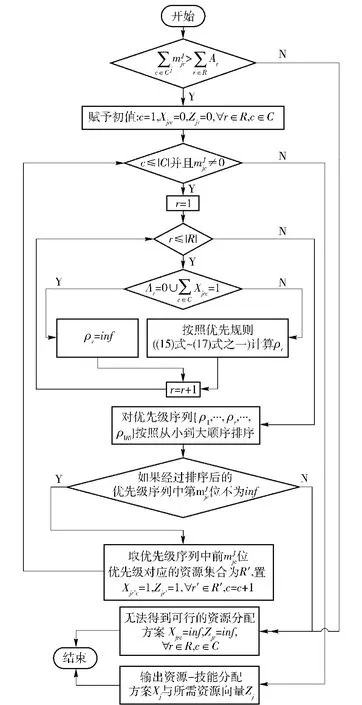
图2 基于优先规则的柔性资源-技能分配算法流程图Fig.2 Flow chart of resources-skills allocation algorithm based on priority rules

2.4 解码过程

该算法中,一个粒子代表一个可行解。算法采用了改进的并行调度生成方案将粒子转化为可行的调度方案。下面介绍改进的并行调度生成方案,它含有柔性资源-技能分配算法,在给出维修任务调度方案的同时还可以安排维修资源的休息时间[13]。

改进的并行调度生成方案最多包含|J|个阶段,阶段n对应一个调度时间tn,一个完工任务集En,一个活动任务集Bn和一个决策任务集Dn.其中完工任务集En是指到tn时刻已经完成的任务组成的集合,即En={j|T′j≤tn};活动任务集Bn是指在tn时刻正在进行的任务组成的集合,即Bn={j|Tj≤tn＜T};决策任务集Dn指在tn时刻满足时序约束的未参加排序的任务组成的集合,即Dn={j|j∉En∪Bn, Pj⊂En};令柔性资源-技能分配算法表示为函数[Xj,Zj]=F(M,A,MR).

具体算法可简单描述为:

解码过程流程图如图3所示。从以上的算法可以看出,维修资源的休息时间是在“当前时间”之前安排的,当其空闲时间长度不小于τ时即进行安排,也就是只要有机会就安排;安排维修资源执行维修任务的时候,不考虑那些如果执行维修任务就可能在本周期段不能休息的维修资源;在每个周期段结束的时候,对那些没有安排休息的资源安排休息。这种算法体现了以维修任务为重,休息时间尽量选择维修资源的空闲时间,必须保证休息时间的思想。

2.5 粒子更新

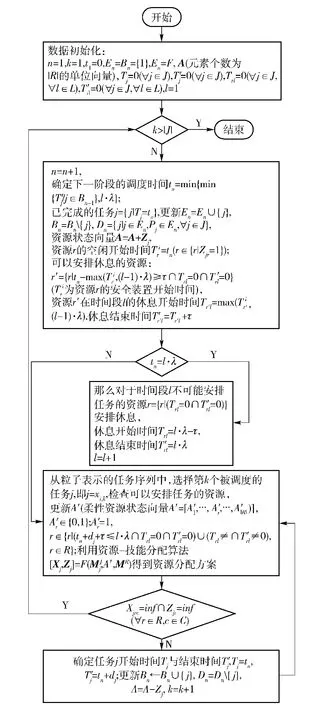
图3 解码过程流程图Fig.3 Flow chart of decode process

算法采用的粒子更新公式[14]为 (19)式～(21)式中:c、、w为算法控制参数。粒子的扰动和粒子的信息继承可分别采用变异或交叉来实现:

1)粒子的扰动。这里引入一种基于任务序列的随机插入法对更新后的粒子xi进行扰动。该方法分为:随机生成一个位置点a1∈[2,|J|-1],设该位置点的任务为xia1,找到该任务的所有紧前任务在此任务序列中的最后位置a2及所有紧后任务在任务序列中最前面的位置a3,然后在a2到a1和a1到a3中随机选择一个位置,将此任务插在该位置。

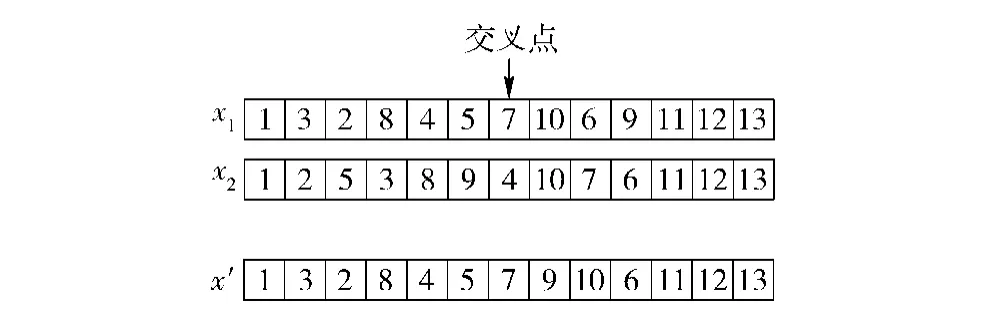
图4 粒子的信息继承Fig.4 Information inheritance of particle

3 计算示例

下面考虑一个维修任务调度实例。该维修任务由13项维修任务组成,由12名维修人员完成,维修资源每工作24 h至少休息8 h.维修人员所具有的技能用资源-技能矩阵表示,如表1所示。第1项任务和最后一项任务分别为虚拟开始和虚拟结束任务,维修任务时间、先后时序约束、所需技能如表2所示。采用本文提出的PSO算法进行求解(资源-技能分配算法中使用了最少技能数资源优先规则),种群规模20,迭代次数80,w=0.75,c′1=0.25, c′2=0.75.

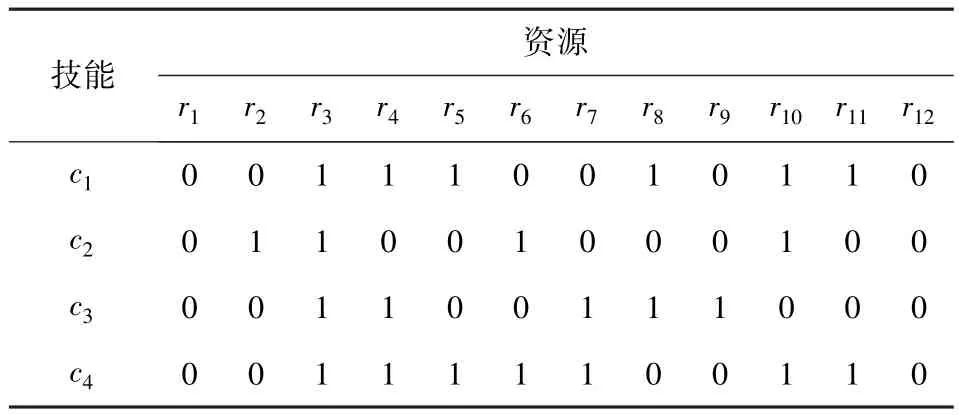
表1 资源-技能矩阵Tab.1 Resources-skillsmatrix

经过计算,求得最优的维修任务序列为:(j1, j3,j4,j2,j5,j6,j8,j7,j9,j10,j11,j12).表3给出了维修任务各项维修任务开工时间和完工时间的进度安排,以及资源-技能分配方案,如:维修任务j2在6 h开始并于10 h结束,完成该任务需要具有技能c1的两单位资源由人员r8、r11负责。休息时间如表4所示。

表2 任务信息Tab.2 Maintenance task information

表3 经优化的维修任务调度方案Tab.3 Optimized maintenance task scheduling plan

维修任务调度方案的甘特图如图5所示,横坐标表示时间,纵坐标表示人员,图中灰色矩形表示维修任务,矩形所处位置的纵坐标对应分配的人员,矩形内部用“-”分割开的3个数字依次表示维修任务编号、人员编号、技能编号;剖面线矩形表示休息时间,矩形内部用“-”分割开的4个数字依次表示时间段编号、人员编号、休息开始时间与结束时间。

表4 休息时间安排Tab.4 Optimized maintenance task scheduling plan

4 结论

本文建立考虑休息的维修任务调度优化模型,并给出了求解该模型的PSO算法,在粒子解码过程中运用了基于优先规则的柔性资源-能力分配模型。并通过具体实例,证明了模型与算法的有效性。该模型适用于决策者同时给出维修任务调度方案与维修资源休息方案。今后,可以研究休息时间可以拆分的维修任务调度模型,以及考虑将最长工作时间约束、人员偏好与休息场所限制纳入到维修任务调度模型中。

References)

[1] 王正元,严小琴,朱昱,等.一种考虑专业的动态维修任务调度的优化方法[J].兵工学报,2009,30(2):252-256.

WANG Zheng-yuan,YAN Xiao-qin,ZHU Yu,et al.An optimal method on dynamicmaintenance task schedulingwith subject taken into account[J].Acta Armamentarii,2009,30(2):252-256. (in Chinese)

[2] 朱昱,宋建社,王正元.一种基于最大保障时间的战时装备维修任务调度[J].系统工程与电子技术,2007,29(11): 1900-1903.

ZHU Yu,SONG Jian-she,WANG Zheng-yuan.Schedulingmodel of the battle equipmentmaintenance task based on themostsupport time[J].Systems Engineering and Electronics,2007,29(11): 1900-1903.(in Chinese)

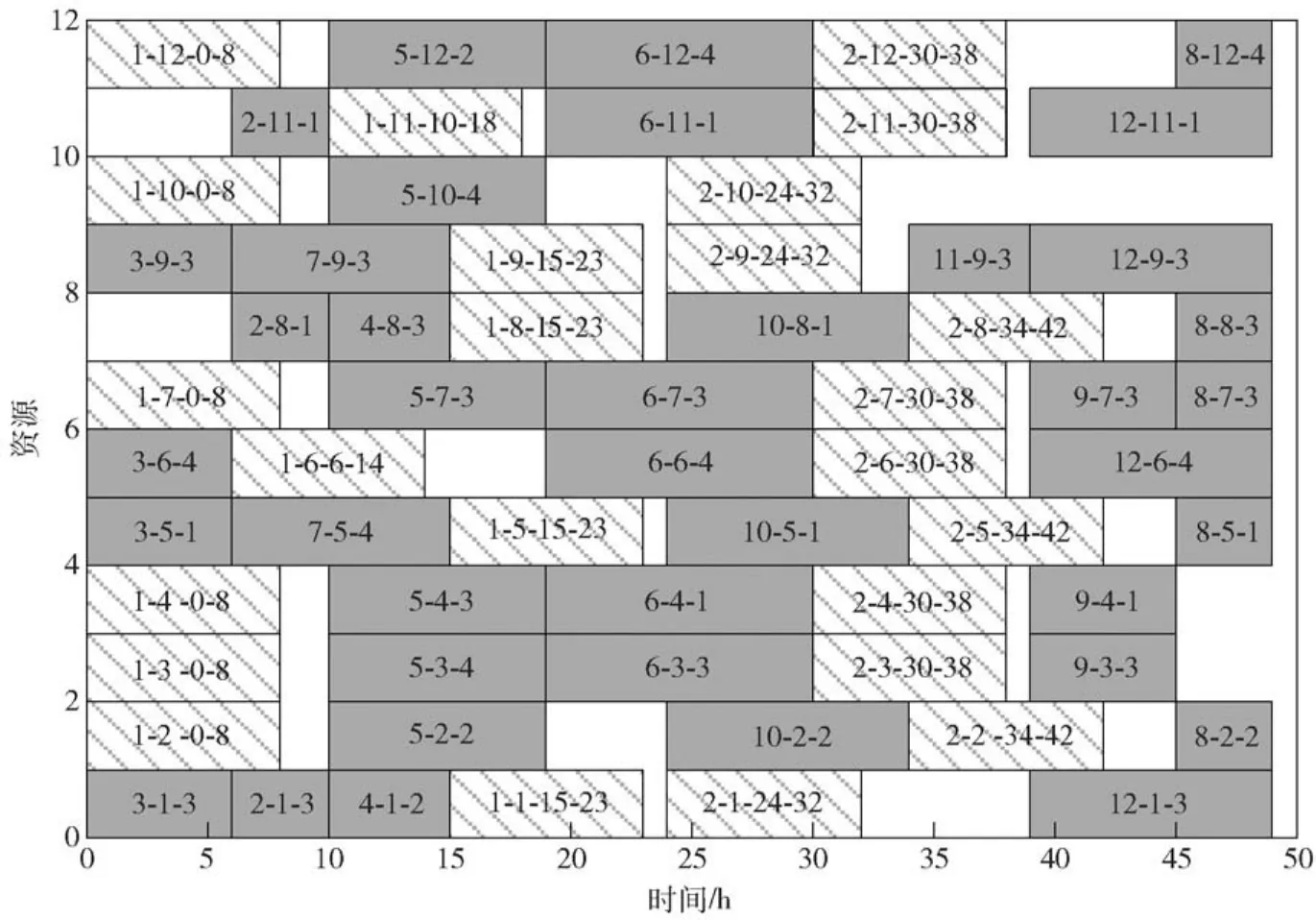
图5 经优化的维修任务调度方案的甘特图Fig.5 Gantt chart of optimized maintenance task scheduling plan

[3] 朱昱,宋建社,曹继平,等.一种考虑装备维修流程的多维修任务调度[J].系统工程与电子技术,2008,30(7):1366-1369.

ZHU YU,SONG Jian-she,CAO Ji-ping,et al.Maintenance task schedulingmodel of multiunit considering armament maintenance process[J].Systems Engineering and Electronics,2008,30(7): 1366-1369.(in Chinese)

[4] Gemmill D.Shop floor scheduling for program depotmaintenance considering stochastic repair needs[R].US:Air Force Office of Scientific Research,2000.

[5] Kolisch R.Serial and parallel resource-contrained project schedulingmethods revisited:theory and computation[J].European Journal of Operational Research,1996,90(2):320-333.

[6] 方晨,王凌.资源约束项目调度研究综述[J].控制与决策, 2010,25(5):641-651.

FANG Chen,WANG Ling.Survey on resource-constrained project scheduling[J].Control and Decision,2010,25(5):641-651. (in Chinese)

[7] Bellenguez-Morineau O.Methods to solve multi-skill project scheduling problem[J].4OR:A Quarterly Journal of Operation Research,2008,6(1):85-88.

[8] Bellenguez O,Ne′ron E.Lower bounds for themulti-skill project scheduling problem with hierarchical levels of skills[J].Lecture Notes in Computer Science,2005,3616:229-243.

[9] 喻小光,战德臣,聂兰顺,等.柔性资源约束的资源水平项目调度问题[J].计算机集成制造系统,2010,16(9):1967-1976.

YU Xiao-guang,ZHAN De-Chen,NIE Lan-shun,et al.Flexible resource constrained resource leveling project scheduling problem [J].Computer Integrated Manufacturing Systems,2010,16(9): 1967-1976.(in Chinese)

[10]黄敏镁,罗荣桂.柔性资源约束下的产品开发项目优化调度研究[J].管理工程学报,2010,24(4):143-148.

HUANG Min-mei,LUO Rong-gui.Study on flexible-resource-constrained product development project scheduling[J].Journal of Industrial Engineering/Engineering Management,2010,24(4): 143-148.(in Chinese)

[11]Zhang H,Li X,Li H.Particle swarm optimization-based schemes for resource-constrained project scheduling[J].Automation in Construction,2005,14(3):393-404.

[12]Jarboui B,Damak N,Siarry P.A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems[J].Applied Mathematics and Computation, 2008,195(1):299-308.

[13]Sprecher A,Kolisch R,Drexl A.Semi-acitive,active,and nondelay schedules for the resource-constrained project scheduling problem[J].European Journal of Operational Research,1995, 80(1):94-102.

[14]潘全科,王凌,高亮.离散微粒群优化算法的研究进展[J].控制与决策,2009,24(10):1441-1449.

PAN Quan-ke,WANG Ling,GAO Liang.The-state-of-art of discrete particle swarm optimization algorithms[J].Control and Decision,2009,24(10):1441-1449.(in Chinese)

[15]邓林义.资源受限的项目调度问题及其应用研究[D].大连:大连理工大学,2008.

DENG Lin-yi.Research on the resource-constrained project scheduling problem with its application abstract[D].Dalian:Dalian University of Technology,2008.(in Chinese)

M aintenance Task Scheduling M odel Considering Rest Time and its Solving Algorithm

LYU Xue-zhi1,CHEN Le2,YIN Jian1,FAN Bao-xin1
(1.Simulation Training Center,Artillery Training Base of the General Staff,Xuanhua 075100,Hebei,China; 2.Department of Command and Management,Equipment Academy,Beijing 101400,China)

As themaintenance resources are periodically used,namely,theymust have rest after running for a period of time,amaintenance task usually is urgent,which must be going on without interruption, how to give outmaintenance task scheduling plan and rest times ofmaintenance resources at same time is an issue being worth to be discussed.A hybrid integer-programming model is established based on the model assumption.A PSO-based solving algorithm is proposed,which includes algorithm framework,particle representation,resources-skills allocation algorithm,particle decoding algorithm and update methods.The validity and feasibility of themodel and resolving algorithm are verified by an example.

ordnance science and technology;maintenance resource;maintenance task;scheduling; PSO algorithm

TP307

A

1000-1093(2014)12-2116-08

10.3969/j.issn.1000-1093.2014.12.027

2013-11-19

吕学志(1979—),男,高级讲师。E-mail:ghostsheep@tom.com