一种基于Herm ite函数约束的光学经纬仪多站定位方法研究

宫志华,徐旭,段鹏伟,雷红

(中国白城兵器试验中心,吉林白城 137001)

一种基于Herm ite函数约束的光学经纬仪多站定位方法研究

宫志华,徐旭,段鹏伟,雷红

(中国白城兵器试验中心,吉林白城 137001)

传统光学几何交会方法中采用的方向余弦定位法因其算法简单清晰一直广泛应用于工程实践,但该方法受空间几何关系影响较大,对测元误差抑制能力差,因此定位精度并不理想,而且不能多站同时定位计算。为此提出一种基于Hermite函数约束的光学经纬仪多站定位解算方法,称为函数约束误差模型弹道最佳估计(EMBET)方法。该方法首先在采用Hermite函数表征目标定位参数以压缩待估参数数量的基础上进而实现对光学经纬仪测元的数学表征,然后将多站多测元观测数据组成联合测量方程,最后依据最小二乘准则优化解算方程获取目标定位参数,并具有对测元系统误差校准的能力。结合仿真实例计算,对方向余弦定位方法和函数约束EMBET方法进行了比较分析,验证了函数约束EMBET方法在光学经纬仪多站定位中具有更高的定位精度和更强的实用性,为工程应用提供了参考依据。

光学；光学经纬仪；时序关联；函数约束；Hermite函数；EMBET

0 引言

光学经纬仪是我国靶场获取外弹道跟踪数据和飞行状态的最基本测量手段之一。由于单台经纬仪只能得到空间目标的二维坐标信息(方位角和高低角),所以为了获得目标在空间中的三维坐标,至少需要两台光学经纬仪以交会方式计算被测目标空中位置。为保证跟踪测试可靠性,采用更多台经纬仪对目标进行跟踪测量是常选的测量方案。现阶段光学经纬仪多采用空间几何交会方法确定目标位置,如目前工程上广泛应用方向余弦定位法[1],亦称为公垂线法、最短距离法[2],或异面交会方法[3],但这种方法对于测元中含有的误差抑制能力差,且受布站几何关系的影响较大,因此定位精度并不很理想。关于两台光学经纬仪的空间几何交会测量问题已得到解决[1-4],但对于3台甚至3台以上光学经纬仪的空间几何交会计算问题尚未有统一的处理方法,如果只选用其中两台经纬仪测量数据进行处理,这造成了一定数据资源的浪费,而且精度上也不能保证最优;文献[5]中阐述的一种对4台光学经纬仪分两侧布站的交会结果进行数据融合的方法,其实质还是在多台经纬仪测量条件下两两组合交会计算,再按一定权值分配方法给出唯一一组数据,虽然交会结果精度会有提高,但这种方法的计算效率非常低。

针对这些问题,本文提出采用基于函数约束的光学经纬仪多站定位方法,称为函数约束误差模型最佳弹道估计(EMBET)方法[6-7],并利用仿真算例,对光学经纬仪传统几何交会和函数约束EMBET定位方法进行了比较分析,结果显示,新方法具有4个方面的优点:一是抑制和探查测元误差能力强;二是降低布站几何关系影响;三是多站能够同时参与定位计算;四是定位精度高。

1 计算模型

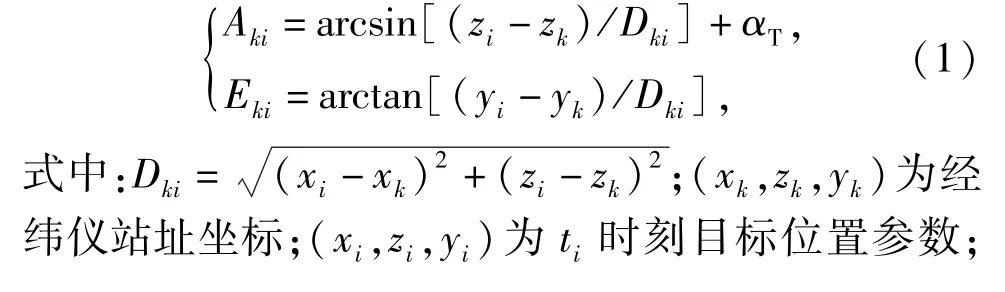
以m台光学经纬仪联合测量目标轨迹为例,则其中第k台经纬仪在ti(i=1,2,…,n)时刻所得测元Aki、Eki与空间坐标(xi,zi,yi)之间的关系式为αT为判象限角。考虑测量方程的非线性,需按泰勒公式展开成线性方程,又因为测量误差(包含系统误差S和随机误差ε)的存在,则由m台经纬仪测得的2m个测元组成的联合测量方程如(2)式所示:

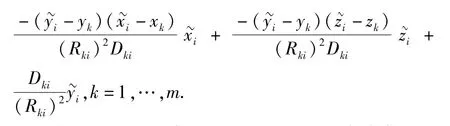
假设系统误差参数有M个,则未知待估参数数量为2(mx+mz+my+6)+M个,方程总数量2mn.可见,当采样数量n一定大时,待估参数被极大压缩,不仅增加测量方程的冗余度,提高方程计算稳定度,而且对各测元系统误差探查和估计能力大大增强。(3)式以矩阵形式给出为

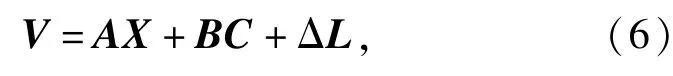
式中:V=(εA1,εE1,…εAm,εEm)T为随机误差向量; X=(βx,βz,βy)T为拟合函数系数向量,即待估参数;A为与X有关的系数矩阵;B为系统误差模型系数矩阵;C为系统误差待估参数向量;ΔL=(A1i-A1i0,E1i-E1i0,…,Ami-Ami0,Emi-Emi0)T为常数向量。

在参数估计时,在大数据量处理的情况下,相关性和非高斯性对估计结果影响不大,因此采用白噪声条件下的参数估计方法。利用最小二乘估计[9-13]可以得到待估参数解X(包括拟合函数待估系数和系统误差模型系数C)和待估参数的误差协方差阵,如(7)式所示:

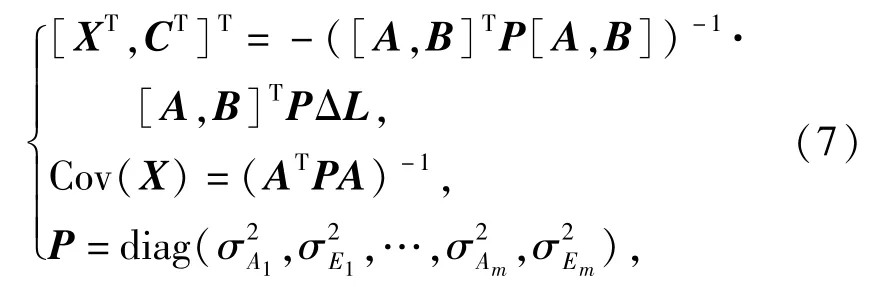
式中:P为权值矩阵,由各测元统计方差相互标定确定。在实际求解中,由于非线性函数级数展开带来的截断误差,需要进行叠代计算。由函数拟合系数代入(4)式,最终得到目标空间位置参数。

2 仿真分析

仿真数据设计:依据质点弹道方程生成某型火箭弹理论弹道,并以其为基准,设计3台光学经纬仪站址(1号站、2号站和3号站)均匀布设在弹道同侧,反推产生3台经纬仪6个真值角度测元,数据率10 Hz,并给每个测元加入相应的随机误差和系统误差值。初值以理论弹道为基础,在x、z、y 3个方向上分别加上300 m、500 m、200 m的固定误差和6 m、6m、8m的随机误差。

2.1 两站定位分析

对加入误差的仿真测元数据分别采用方向余弦定位方法和函数约束EMBET方法进行两站定位计算,每种解算方法得到3组弹道坐标数据,取平均值与理论弹道真值进行比对,误差曲线如图1所示,误差统计值见表1.仿真加入的随机误差和系统误差真值以及探查出的随机误差和系统误差值见表2.

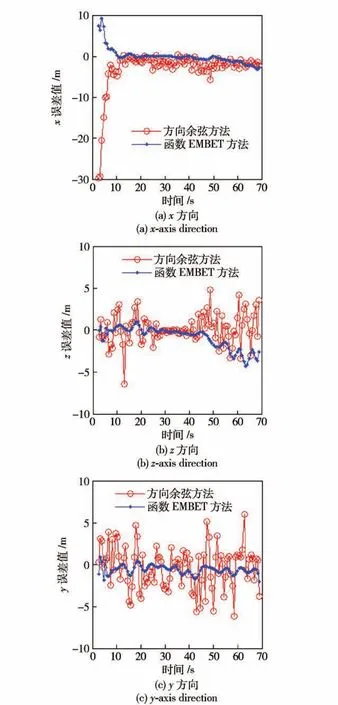
图1 两种定位方法两站定位误差曲线Fig.1 The positioning error curves of twomethods for two optical theodolites

从图1和表1中看到,在两站定位条件下,方向余弦定位方法的定位总误差计算值达到6.3 m,而函数约束EMBET方法的定位总误差计算值2.4m,定位精度比方向余弦定位方法提高1倍以上;从表2中看到,所有测元随机误差探查的最大误差计算值是0.7″,系统误差探查的最大误差计算值达到12.1″,可见,系统误差探查的准确度不高。

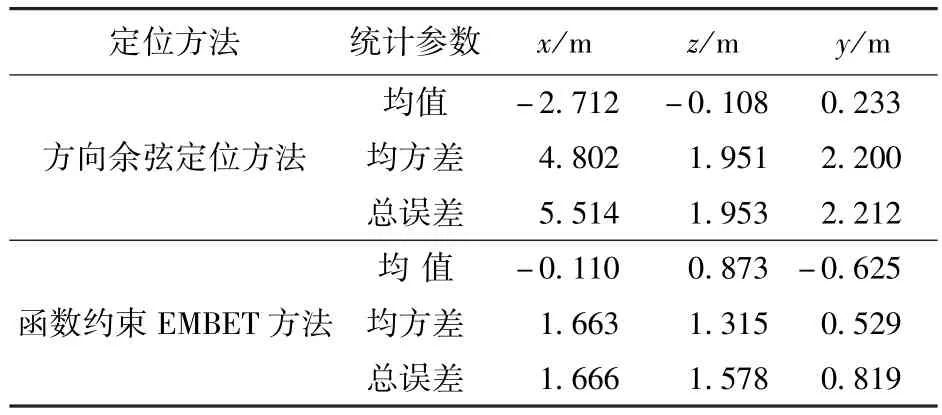
表1 两种定位方法两站定位误差统计Tab.1 The positioning error statistics of twomethods for two optical theodolites

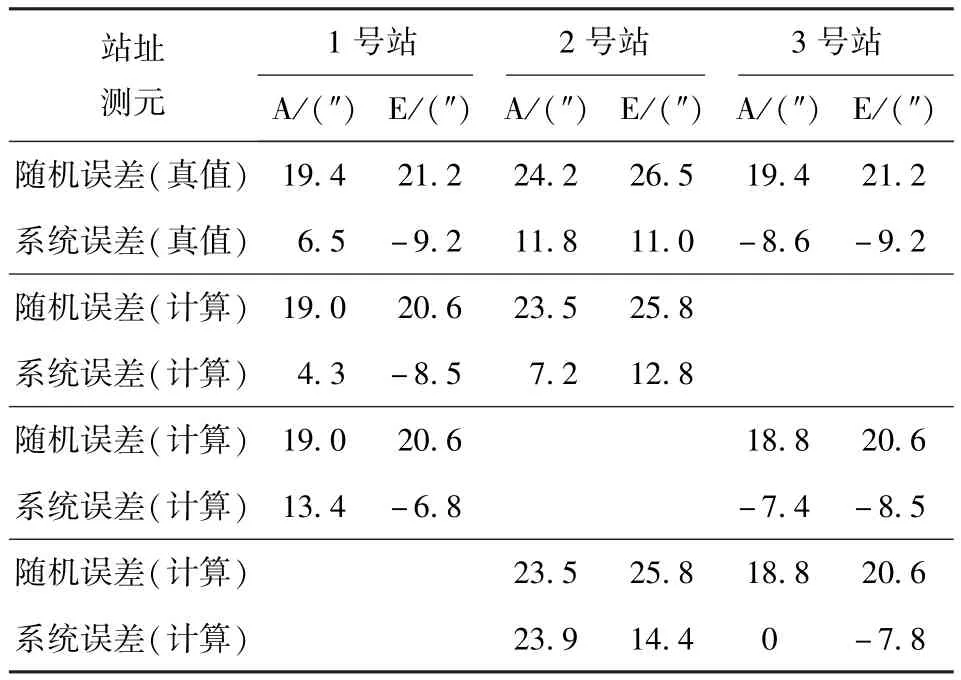
表2 函数约束EMBET方法两站解算测元随机误差和系统误差统计Tab.2 The random error and system error statistics ofmeasuring elements got by function restriced EMBET method with two optical theodolites

2.2 三站定位分析

对加入误差的仿真测元数据采用函数约束EMBET方法进行三站定位计算,与理论弹道真值进行比对,误差曲线如图2所示,误差统计值见表3,探查出的随机误差和系统误差值见表4。

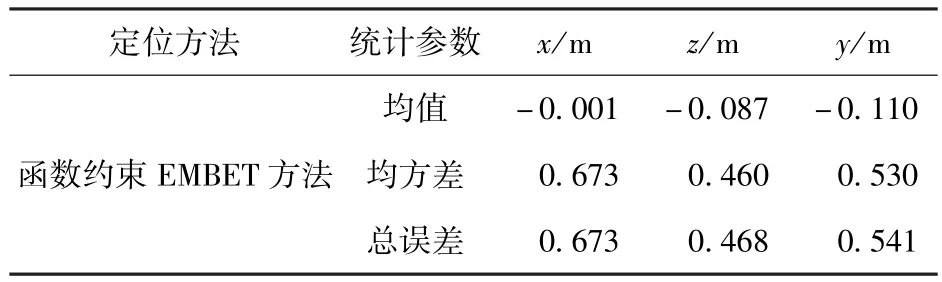
表3 函数约束EMBET方法三站定位误差统计Tab.3 The positioning error statistics of function restriced EMBETmethod for three optical theodolites

从图2和表3中看到,应用函数约束EMBET方法,三站定位总误差计算值只有0.98 m,定位精度比两站定位提高1倍以上;从表4中看到,所有测元随机误差探查的最大误差计算值还是0.7″,但系统误差探查的最大误差计算值只有1.3″,可见,系统误差探查的准确度得到极大提高。

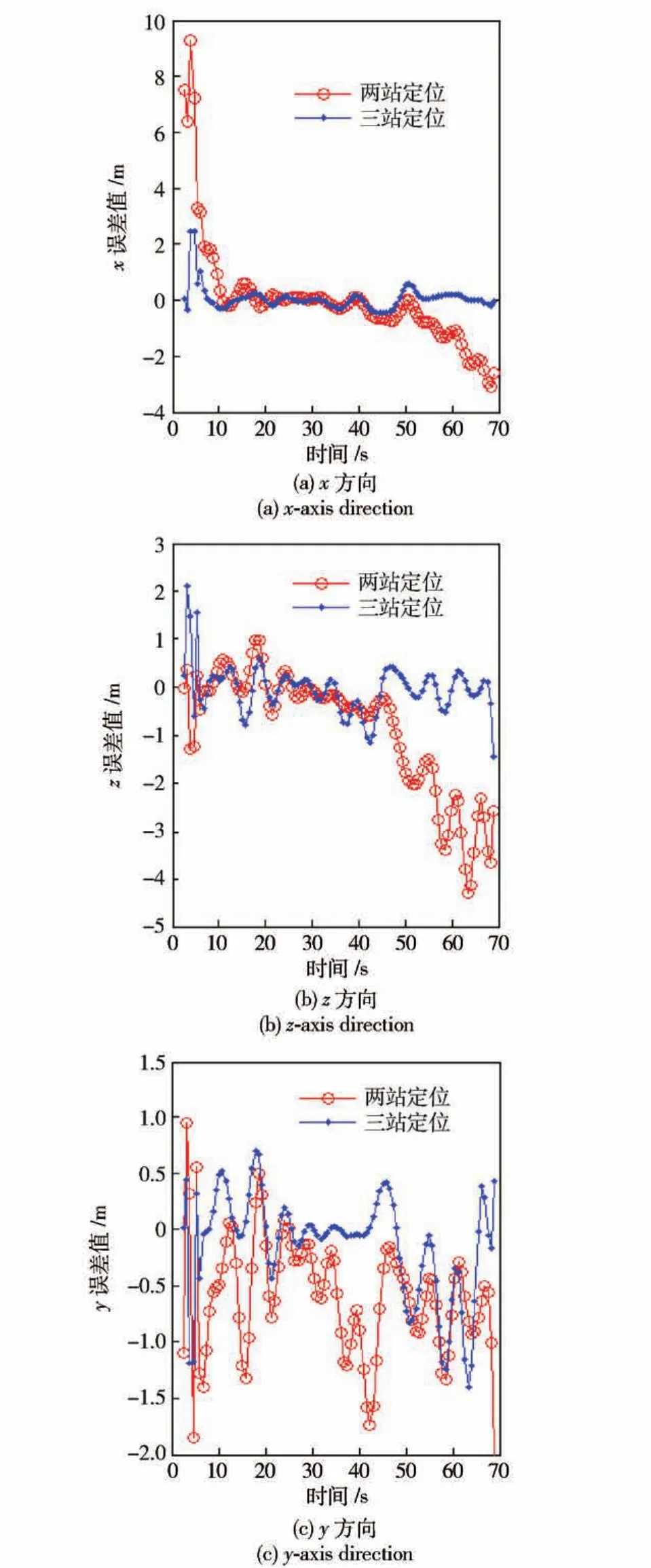
图2 函数约束EMBET方法三站定位误差曲线Fig.2 The positioning error curves of function restriced EMBETmethod for three optical theodolites

采用函数约束EMBET方法对四站经纬仪进行仿真计算,定位总误差为0.87m,所有测元随机误差探查的最大误差0.7″,系统误差探查的最大误差1.1″,可见,定位精度和误差探查准确度进一步提高,但提高幅度已经不大了。

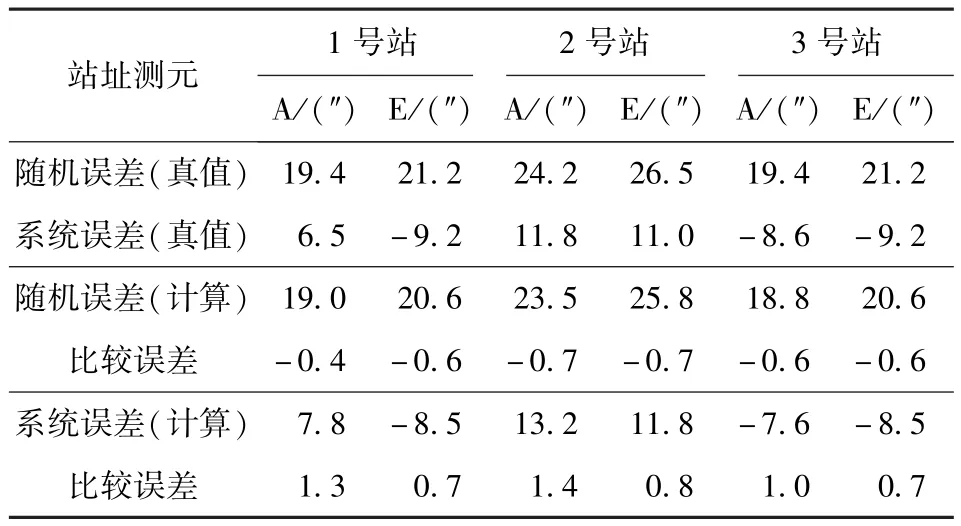
表4 函数约束EMBET方法三站定位测元随机误差和系统误差统计Tab.4 The random errors and system error statics ofmeasuring elements got by function restriced EMBET method for three optical theodolites

3 结论

通过以上仿真计算分析,可以得到如下结论:

1)仅就两站定位来说,方向余弦定位方法受随机误差和系统误差影响大,而函数约束EMBET方法由于对待估参数进行了极大压缩,受随机误差影响降低,因此,定位精度得到提高;函数约束EMBET方法在两站定位时,由于参与计算的测元少,冗余程度不高,系统误差探查的准确度不高;从计算效率来看,方向余弦定位方法和函数约束EMBET方法计算效率都很高。

2)多站(大于两站)同时定位时,方向余弦定位方法不能实现同时定位计算,函数约束EMBET方法定位精度更高,且优于两站定位精度;函数约束EMBET方法在多站定位时,由于参与计算的测元增多,冗余程度增强,具有了较强的系统误差探查和校准能力,系统误差探查的准确度较高。

综合以上结论,在靶场工程应用时,方向余弦定位方法和函数约束EMBET方法在两站定位时,都具有较强的实用性,精度也可以,但函数约束EMBET方法对系统误差还具有了一定的探查和校准能力;在多站定位时,函数约束EMBET方法具有更强的实用性,系统误差探查能力强,且对初值要求不高,因此,在高精度定位和设备校准等方面具有很大的工程应用价值。

References)

[1] 刘利生,李杰.外测数据事后处理[M].北京:国防工业出版社,2000.LIU Li-sheng,LI jie.Post-flight data processing of trajectorymeasurement[M].Beijing:National Defense Industry Press,2000.(in Chinese)

[2] 贾涛,赵长寿.光测设备交会计算最优方法研究[J].兵器试验,1999,183(3):1-14.

JIA Tao,ZHAO Chang-shou.A study on the optimized intersection method of optical theodolite[J].Ordance Test,1999,183(3):1-14.(in Chinese)

[3] 吴能伟,陈涛.异面交会法在光电经纬仪中的应用[J].仪器仪表学报,2006,27(6):15-21.

WU Neng-wei,CHEN Tao.Application of non-coplane intersection method to photoelectric theodolite[J].Chinese Journal of Scientific Instrurment,2006,27(6):15-21.(in Chinese)

[4] 侯宏录,李宏.光电经纬仪测量飞行器三维坐标方法及误差分析[J].光电工程,2002,29(3):4-8.

HOU Hong-lu,LIHong.Measurement of vehicle three dimension coordinate with photoelectrical theodolite and error analysis[J]. Opto-Electronic Engineering,2002,29(3):4-8.(in Chinese)

[5] 张玲霞,马彩文,陈明,等.靶场光电经纬仪多台交会测量数据的一种处理方法[J].测绘学报,2003,32(2):139-142.

ZHANG Ling-xia,MA Cai-wen,CHEN Ming,et al.A data processingmethod on trajectorymeasurement by intersection in shooting range[J].Acta Geodaetica et Cartographica Sinica,2003,32 (2):139-142.(in Chinese)

[6] 王正明,易东云,周海银.弹道跟踪数据的校准与评估[M].长沙:国防科技大学出版社,1999.

WANG Zheng-ming,YIDong-yun,ZHOU Hai-yin.Tracking trajectory data calibrating and evaluating[M].Changsha:Publishing House of National University of Defense Technology,1999.(in Chinese)

[7] 郭军海.弹道测量数据融合技术[M].北京:国防工业出版社社,2012.

GUO Jun-hai.Trajectory data fusion technology[M].Beijing:National Defense Industry Press,2012.(in Chinese)

[8] 詹武平,谌廷政,刘成,等.组网雷达测量色噪声数据的Hermite插值融合方法[J].现代雷达,2012,34(6):41-44.

ZHANWu-ping,SHEN Ting-zheng,LIU Cheng,et al.Hermite interpolation fusion method for netted radar measuring colored noise data[J].Modern Radar,2012,34(6):41-44.(in Chinese)

[9] 吴泽民,任姝婕.雷达时差和系统误差的联合估计方法[J].兵工学报,2011,32(7):848-852.

WU Ze-min,REN Shu-jie.Jointestimation for time offsetand radar system error[J].Acta Armamentarii,2011,32(7):848-852.(in Chinese)

[10] 柴敏,余慧,宋卫红,等.光学无线电测量信息融合定位方法[J].光学学报,2012,32(12):158-164.

CHAIMin,YU Hui,SONG Wei-hong,et al.Joint positioning method for data fusion of photo-electric theodolite and radar[J]. Acta Optica Sinica,2012,32(12):158-164.(in Chinese)

[11] 崔书华,胡绍林,宋卫红,等.多测速系统最优弹道估计方法及应用[J].弹箭与制导学报,2012,32(4):215-218.

CUIShu-hua,HU Shao-lin,SONGWei-hong,et al.Optimal estimation and application of velocitymeasurement system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(4): 215-218.(in Chinese)

[12] 崔书华,许爱华,赵树强,等.高精度跟踪测量系统测元数据融合处理方法[J].弹箭与制导学报,2013,33(3):167-170.

CUIShu-hua,XU Ai-hua,ZHAO Shu-qiang,et al.Fusion processingmethod ofmeasurement elements in high-precision trackingmeasuring system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(3):167-170.(in Chinese)

[13] 宫志华,周海银,郭文胜,等.基于样条函数表征目标运动轨迹事后数据融合方法研究[J].兵工学报,2014,35(1):120-127.

GONG Zhi-hua,ZHOU Hai-yin,GUOWen-sheng,et al.Data fusion algorithm for target trajectory determination based on spline function representation[J].Acta Armamentarii,2014,35(1): 120-127.(in Chinese)

Research on the Positioning M ethod of M ulti-optical Theodolites Based on Herm ite Function Restriction

GONG Zhi-hua,XU Xu,DUAN Peng-wei,LEIHong
(Baicheng Ordnance Test Center of China,Baicheng 137001,Jilin,China)

The direction cosine locationmethod which is used in traditional optical geometric intersection is simple,so it iswidely used in engineering practice.But thismethod is greatly influenced by the geometric relationship,and cannot inhibit themeasuring error,so its positioning accuracy is unsatisfactory. In addition,it cannot be used to compute the locationswithmore than three stations at a time.A new positioningmethod with multi-optical theodolites is proposed based on Hermite function restriction.This method can be called function restricted EMBETmethod.Thismethod uses Hermite function to express the positioning parameters to compress the number of parameters to be estimated,and meanwhile the measuring elements of optical theodolite can be expressed.The measuring equation can be formed by measuring data ofmultiplemeasuring elements.Based on least square criterion,the positioning parameters are obtained by computing the combined equation,and the system errors ofmeasuring elements are calibrated.Through the calculation of simulated example,the function restricted EMBETmethod is compared with the direction cosine location method.The result shows that the function restricted EMBET method ismore accurate and more practical.

optics;optical theodolite;time sequence relevance;function restriction;Hermite function;errormodel best estimate of trajectory

V557+.4

A

1000-1093(2014)12-2092-06

10.3969/j.issn.1000-1093.2014.12.023

2014-01-07

宫志华(1975—),男,高级工程师。E-mail:gzh63298@126.com