多孔介质水平分层海底低频地震波的数值模拟

卢再华,张志宏,顾建农

(海军工程大学理学院,湖北武汉 430033)

多孔介质水平分层海底低频地震波的数值模拟

卢再华,张志宏,顾建农

(海军工程大学理学院,湖北武汉 430033)

舰船低频辐射噪声在海底岩土层中引起的弹性波被称为舰船地震波,可用于识别舰船目标。为获取浅海厚沉积层环境下舰船地震波的传播特性,基于多孔介质波动理论建立海底地震波的三维交错网格有限差分算法,对多孔介质海底低频声源激励的海底地震波进行数值计算。计算结果表明:近场范围内,多孔介质海底地震波的波动成分主要有透射快纵波、透射横波、透射慢纵波和海底界面波；对于远场地震波而言,海水层的波导效应逐渐表现出来,海底地震波的波动成分主要是沿水平方向传播的简正波和海底界面波。

振动与波；多孔介质；低频；浅海；地震波；交错网格

0 引言

航行舰船在海底岩土层中引起的弹性波被称为舰船地震波,主要由舰船低频辐射噪声引起,可用于识别舰船目标[1]。为了获取舰船地震波的传播特性,研究人员对低频声源激励的海底地震波进行了理论分析[2-4]。这些理论分析将浅海海底介质视为单相的液体或固体弹性介质,难以较好地反映浅海沉积层的多孔介质特性和波动传播规律。实际浅海多数存在较厚的沉积层,中国南海北部大陆架浅海沉积层的试验结果表明,沉积层厚约60 m,通常为淤泥、淤泥质亚粘土、亚粘土、砾石亚粘土、粉砂等未固结或半固结岩土层,是典型的饱水两相多孔介质[5]。为了更好地掌握低频声信号在浅海厚沉积层环境中的传播规律,基于多孔介质波动理论进行研究是必要的。数值模拟是研究弹性波波场特征和传播规律的重要手段,其中交错网格有限差分法在石油地球物理勘探等研究领域已获得较为广泛的应用[6-7]。由于低频声源激励浅海地震波在应用领域上存在一定的特殊性,相关的时域数值模拟比较少见。据此,本文采用交错网格有限差分法,基于多孔介质波动理论对低频声源激励的浅海地震波的进行时域内的数值模拟,以进一步明确舰船地震波的形成机理和传播过程,为舰船地震波在水中目标探测领域的应用和发展提供理论基础。

1 交错网格高阶有限差分算法

将海底沉积层视为各向同性饱和的孔隙弹性介质,根据广义胡克定律得到应力应变关系式为

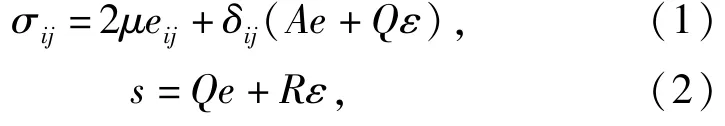
式中:σij和eij=(ui,j+uj,i)/2分别为固相骨架的应力张量和应变张量;μ、A、Q、R为Biot多孔介质弹性常数;δij是Kronecker符号;固相骨架和孔隙液体的体积应变分别为e=ui,i和ε=Ui,i,u和U分别为固相和液相的质点位移;s=-φp为孔隙流体的有效压力,与孔隙率φ和孔隙流体的压强p有关。在不考虑外加力作用时,固相的应力位移关系为

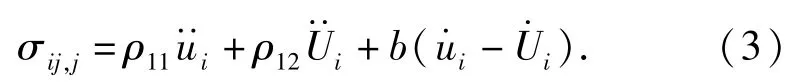
液相的应力位移关系则满足广义Darcy定律,即

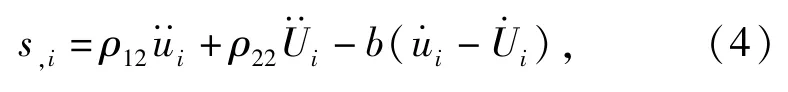
式中:ρ11=(1-φ)ρs+ρa;ρ12=-ρa;ρ22=φρf+ρa; ρa、ρs和ρf分别为固相与流相间耦合密度、固相密度和流相密度;耗散系数b=ηφ2/k,η为液体的粘性系数,k为渗透系数,变量上方的单圆点和双圆点分别表示对时间的1阶和2阶导数。

由以上两个应力位移关系式可以得到质点速度的1阶波动方程,

(5)式～(8)式构成速度-应力表达的饱和孔隙介质1阶弹性波动方程。

根据交错网格有限差分法原理,利用Taylor公式,可以将上述波动方程中速度或应力对时间的1阶导数展开成时间差分近似。以速度vx对时间的1阶导数为例,具有2M阶精度的时间差分表达式为

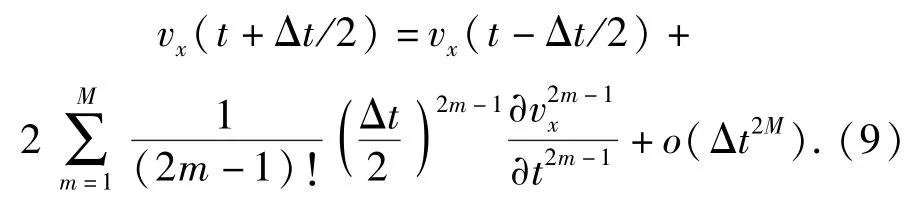
类似地,速度或应力对空间的1阶导数也可以用如下具有2N阶精度的空间差分来表达,以x方向的导数为例:

一般地,速度或应力对时间的导数采用2阶精度的差分近似比较合适,对空间的导数则应该采用较高的阶数,可以明显地提高算法的精度和抑制数值计算过程中的频散现象[8]。据此,本文采用时间2阶、空间10阶的交错网格高阶差分算法进行分析。在交错网格技术中,速度和应力等地震波波场分量在空间位置和时间节点上相互交错分布。对于三维问题,波场分量和孔隙介质弹性参数在空间位置上的交错分布如图1所示;在时间节点上应力通常位于整数倍时间步长,而速度需和应力错开半个时间步长。

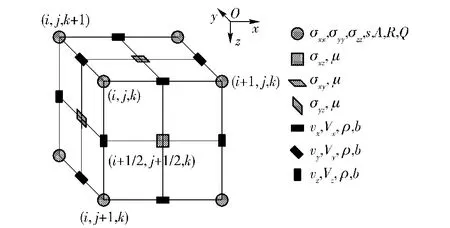
图1 交错网格中波场分量和弹性参数的分布示意图Fig.1 Discretized variables and elastic constants on staggered grid

根据上述约定,以x方向速度为例,(5)式和(6)式的三维交错网格差分格式如下:

类似地,以x方向正应力和液相有效压力为例, (7)式和(8)式的差分格式如下:

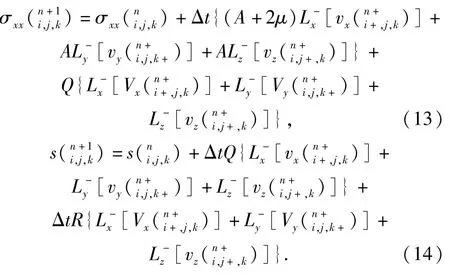
(11)式～(14)式中:速度分量vx()括号内的上标n+代表离散的时间节点为(n+1/2)Δt,下标i+、j和k代表离散的空间位置为(i+1/2)Δx、jΔz和kΔy;Δx、Δy、Δz和Δt分别为空间、时间的离散步长;分别为σxx在x方向的空间差分和σxy在y方向的空间差分,差分算子的上标+和-号代表向前差分和向后差分。其他差分算子同上面约定,其余的速度分量、应力分量的差分格式同理可得。

海底地震波在半无限区域中进行传播,而在地震波的数值计算过程中,受计算机存储容量和速度等运行环境限制,只能在有限区域内进行计算,这种有限区域的边界包括自由表面和人为截断的边界(人工边界)。进行数值模拟时,必需对自由表面和人工边界进行处理,否则影响数值模拟结果的可靠性。本文采用Collino等提出的完全匹配层(PML)方法[9]实现人工边界,其基本思想是将地震波场分裂为不同坐标轴方向的几个部分,在匹配层边界内按不同的坐标轴方向进行衰减。以vx的波动方程为例,根据PML的波场分裂思路,将vx分裂为、和3个部分,vx=++,上标代表该项只与相应方向的空间导数有关,得到不考虑耗散影响的PML吸收边界方程如下:

式中:d(x)、d(y)和d(z)分别为匹配层内在x、y和z方向的衰减因子;σxx,x表示σxx在x方向的空间导数,s,x表示s在x方向的空间导数,其他以此类推。然后,按照交错网格有限差分法对上式进行离散,即可得到PML吸收边界方程的差分格式,限于篇幅不再列出。

在自由表面上,应力必须满足自由表面边界条件,即所有应力分量为0.本文采用应力镜像法,通过在自由面上方设置虚拟层,将自由面以下的应力镜像到虚拟层中,实现自由面应力为0的边界条件。

海水层视为理想流体介质,其波动方程可以由多孔介质弹性波动方程退化得到,即(1)式中,A取为流体的体积压缩模量K=ρc2,ρ和c分别为流体密度和声速;其他弹性常数μ、Q和R取为0.震源采用余弦包络脉冲子波,波形函数为

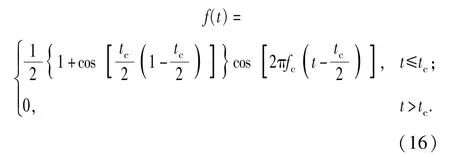
式中:fc和tc分别为脉冲子波的中心频率和带宽参数。

2 数值算例及分析

为了考察本文有限差分算法的合理性,首先对多孔介质海底中点源激励的海底地震波进行了数值计算(算例1)。如图2所示,整个计算域的长、宽均为1 200m,深度方向为1 000m,网格大小均为5m,时间步长为0.5ms.计算模型的前后左右和下部设置PML吸收边界层,层厚均为10个网格。上部海水层厚度为100m,海水层密度1 000 kg/m3,声速为1 500m/s.震源采用胀缩应力源,波形函数为余弦包络脉冲子波,中心频率40 Hz,带宽80 Hz,设置在模型中心,深度为400 m处。波场快照记录时间为0.25 s.多孔介质海底的孔隙率为0.39,物性参数如表1所示[10]。

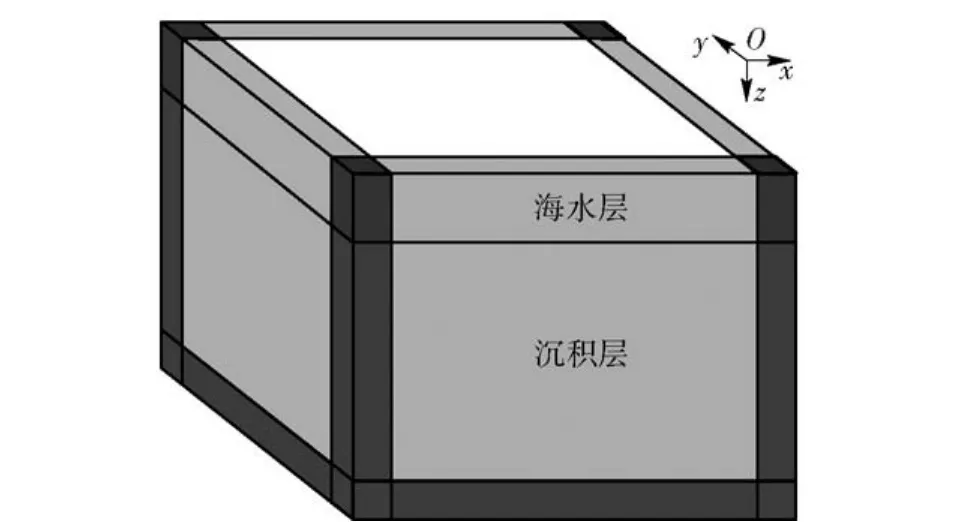
图2 浅海PML吸收层边界示意图Fig.2 Sketch of PML boundary in a shallow sea

表1 Biot双相各向同性介质物性参数Tab.1 Parameters of a homogeneous saturated porous sediment

图3 固相竖直速度波场快照(t=0.25 s)Fig.3 Snapshot of solid particle vertical velocity wavefield(t=0.25 s)

图3和图4分别为固相和液相竖直速度在Oxz平面内的波场快照。由于震源采用胀缩应力源,直达波场中没有产生横波成分,只存在着两类纵波,直达快纵波P2和慢纵波SP2(下标2代表波动所在的介质层,下同)。快纵波在固相和流相中的相位相同,而慢纵波在固相和流相中的相位相反。左右和下部的PML吸收边界较好地实现了快纵波向计算域外的无反射传播。直达快纵波P2向上传播到海底后,产生向海水层传播的透射纵波P2P1和向下传播的3种转换波,分别为反射快纵波P2P2、反射横波P2S2和反射慢纵波P2SP2.反射慢纵波在流相中振幅大,而在固相中的振幅较小,即在相同条件下,从流相中更容易观测到慢纵波。向海水层传播的透射纵波P2P1经由自由面反射后,形成向下传播的纵波P2P1P1.上述传播特征与Biot理论得出来的结论[11]基本一致,说明本文有限差分算法的有效性,对人工边界、海底界面和自由面边界的处理也是合理的。

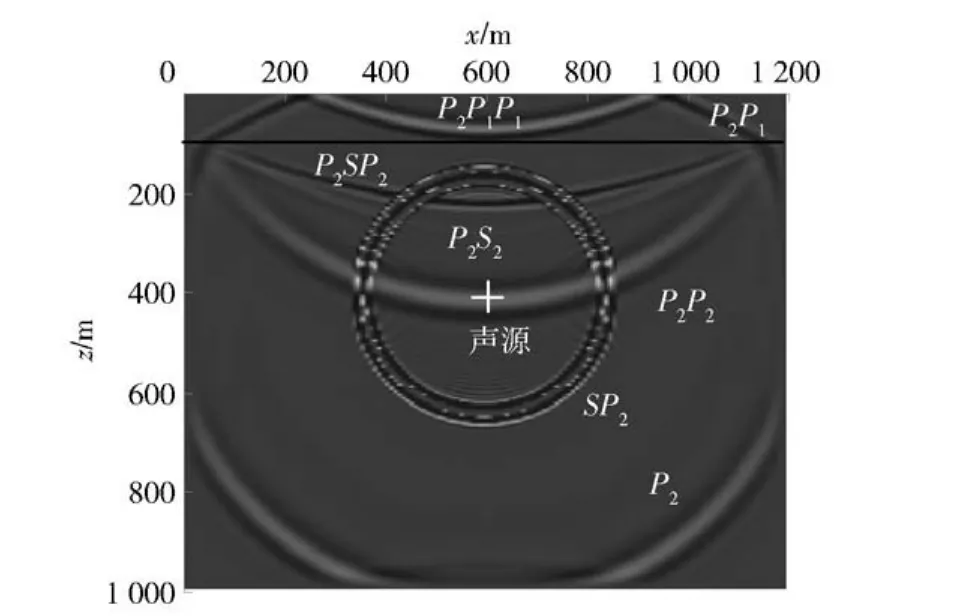
图4 液相竖直速度波场快照(t=0.25 s)Fig.4 Snapshot of liqiud particle vertical velocity wavefield(t=0.25 s)

将验证算例1中的胀缩应力源改为海水层中的脉冲声源,声源深度取为88 m,计算区域大小再相应调整,即可对低频声源在多孔介质海底中激励的海底地震波进行数值模拟。首先,对声源附近的近场波动进行了算例2的数值计算。图5和图6分别为固相和液相竖直速度在Oxz平面内的波场快照。可见,脉冲声源在海水层中激励出直达纵波P1后, P1经海底表面反射产生上行纵波,P1经自由面反射形成下行纵波P1P1.在多孔介质海底中,直达纵波P1在海底表面发生透射,产生的转换波主要有透射快纵波P1P2、透射横波P1S2和透射慢纵波P1SP2.另外,在海底表面附近还形成了海底界面波,其波动能量局限于海底表面附近,随着远离海底表面波幅迅速衰减。可见,近场范围内传播距离较短,各种波动成分的衰减不大,多孔介质海底中地震波的波动成分主要有透射快纵波、透射横波、透射慢纵波和海底界面波,海水层内则主要是经海底表面、自由面的反射后形成的上行纵波、下行纵波。

图5 固相竖直速度波场快照(t=0.13 s)Fig.5 Snapshot of solid particle vertical velocity wavefield(t=0.13 s)

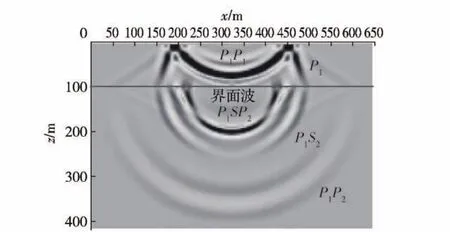
图6 液相竖直速度波场快照(t=0.13 s)Fig.6 Snapshot of liqiud particle vertical velocity wavefield(t=0.13 s)

算例3对低频声源激励的远场地震波进行了数值模拟,声源的中心频率为20 Hz,带宽40 Hz,声源深度为80m,计算域的水平横距取为1 800m.图7和图8分别为固相的水平速度和竖直速度在Oxz平面内的波场快照。可见,当声源激励的波动传播到较远距离后,波场快照中主要存在两个波群。对于横距1 200m附近的波群,幅值随着远离海底表面迅速衰减,应为海底界面波。对于横距1 500 m附近的波群,幅值空间分布规律和左边的界面波明显不同,水平速度的波形基本限制在海水层内,在海水层中间深度达到最大幅值;竖直速度在海水层中间深度发生反相,这些幅值的空间分布规律符合海水层内1阶简正波的传播特征。实际上,当海水层内的上行波、下行波传播到远场后,波阵面曲率变得很小,沿竖直方向基本失去传播特性,形成主要沿水平方向进行传播的波群,通常称为简正波或模式波[12-13]。

图7 固相水平速度波场快照(t=1.1 s)Fig.7 Snapshot of solid particle horizontal velocity wavefield(t=1.1 s)

图8 固相竖直速度波场快照(t=1.1 s)Fig.8 Snapshot of solid particle vertical velocity wavefield(t=1.1 s)

根据Biot多孔介质理论[11],慢纵波衰减大,只能在近距离传播。多孔介质海底中的透射快纵波、透射横波为球面波,空间衰减较大,也不利于远距离传播。海底界面波局限于海底表面附近传播,简正波主要在海水层波导内传播,相对而言能传播到较远距离。上述模拟结果表明,对于远场地震波而言,海水层的波导效应逐渐表现出来,海底地震波的波动成分主要是沿水平方向传播的简正波和海底界面波。图9和图10分别为固相的水平速度和竖直速度在海底表面Oxy平面内的波场快照,图中两种波动成分表现得更加明显。根据上述3个算例,和单相弹性海底中的地震波传播相比,多孔介质海底的直达波和转换波场中都出现了慢纵波成分,但慢纵波衰减大,只能在近距离传播。在远场范围,两种海底介质条件下地震波的波动成分差别不大,均为沿水平方向传播的简正波和海底界面波。

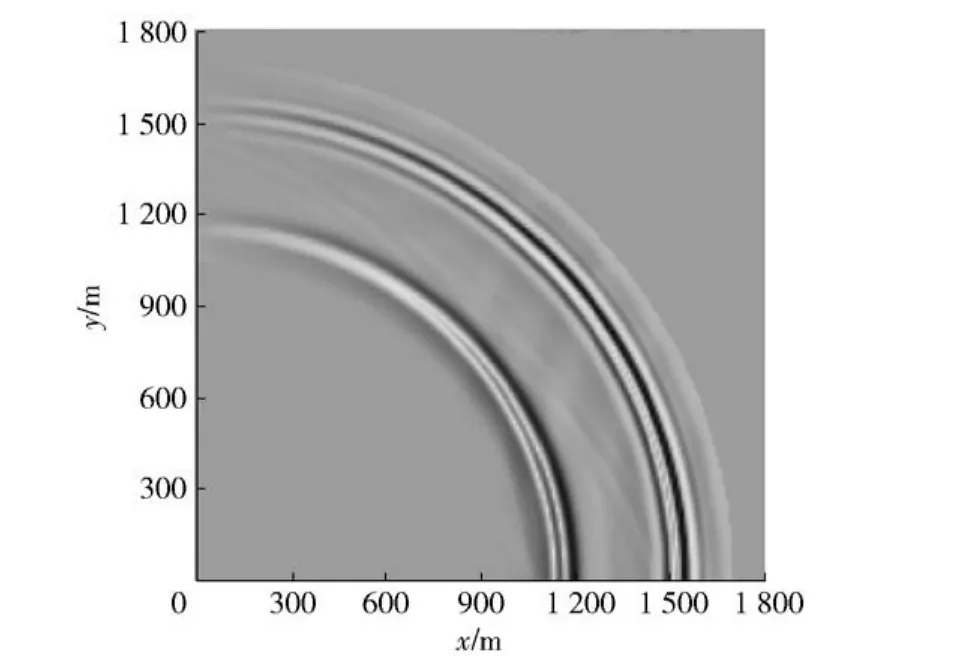
图9 固相水平速度波场快照(t=1.1 s)Fig.9 Snapshot of solid particle horizontal velocity wavefield(t=1.1 s)

图10 固相竖直速度波场快照(t=1.1 s)Fig.10 Snapshot of solid particle vertical velocity wavefield(t=1.1 s)

3 结论

为获取浅海厚沉积层下舰船地震波的传播特性,本文基于多孔介质波动理论,建立了海底地震波的三维交错网格有限差分算法。对多孔介质海底低频声源激励的海底地震波进行了时域内的正演数值模拟,根据数值模拟的结果,得出以下结论:

1)近场范围内,多孔介质海底中地震波的波动成分主要有透射快纵波、透射横波、透射慢纵波和海底界面波,海水层内则主要是经海底表面、自由面反射后形成的上行纵波、下行纵波。

2)当海水层内的上行波、下行波传播到远场后,波阵面曲率变得很小,沿竖直方向基本失去传播特性,形成主要沿水平方向在海水层中进行传播的简正波。

3)慢纵波衰减大,只能在近距离传播;多孔介质海底中的透射快纵波、透射横波为球面波,空间衰减较大,也不利于远距离传播;海底界面波局限于海底表面附近传播,简正波主要在海水层波导内传播,相对而言能传播到较远距离。

4)对于远场地震波而言,海水层的波导效应逐渐表现出来,海底地震波的波动成分主要是沿水平方向传播的简正波和海底界面波。

低频声源激励浅海地震波的波动成分和传播规律比较复杂,本文主要是建立了三维问题的交错网格有限差分算法,初步分析了近场和远场海底地震波的波动成分。声源频率、声源深度、海水层厚度、海底软硬程度和衰减大小等对多孔介质海底地震波特性的影响规律,还需进一步进行数值计算和分析。典型的三维海底为楔形海底,是海底低频地震波在工程应用领域的一种主要海洋环境,将本文计算模型推广应用到楔形或倾斜海底的地震波传播问题,对舰船地震波的理论研究具有重要意义。

References)

[1] 卢再华,张志宏,顾建农.舰船海底地震波及其在水雷引信中的应用[J].水雷战与舰船防护,2004(4):25-28.

LU Zai-hua,ZHANG Zhi-hong,GU Jian-nong.The ship-induced seismic wave on the seafloor and it's application in water mine fuze[J].Mine Warfare and Ship Self-defence,2004(4):25-28.(in Chinese)

[2] 颜冰,周伟,龚沈光.浅海地震波传播的简正波模型[J].武汉理工大学学报,2006,30(5):805-807.

YAN Bing,ZHOU Wei,GONG Shen-guang.A normal mode model for ocean seismo-acoustics in shallow water[J].Journal of Wuhan University of Technology,2006,30(5):805-807.(in Chinese)

[3] 卢再华,张志宏,顾建农.基于波数积分的点声源海底地震波计算方法研究[J].武汉理工大学学报,2011,35(1): 118-121.

LU Zai-hua,ZHANG Zhi-hong,GU Jian-nong.An algorithm for seismic wave on seafloor caused by low frequency point sound source based on wave-number integration technique[J].Journal of Wuhan University of Technology,2011,35(1):118-121.(in Chinese)

[4] 张海刚,朴胜春,杨士莪.水中甚低频声源激发海底地震波的传播[J].哈尔滨工程大学学报,2010,31(7):879-887.

ZHANG Hai-gang,PIAO Sheng-chun,YANG Shi-e.Propagation of seismic waves caused by underwater infrasound[J].Journal of Harbin Engineer University,2010,31(7):879-887.(in Chinese)

[5] 卢博,李赶先.用声学三参数判别海底沉积物性质[J].声学技术,2007,26(1):6-14.

LU Bo,LIGan-xian.Discrimination of seafloor sediment properties from sound velocitywaveform and amplitude[J].Technical A-coustics,2007,26(1):6-14.(in Chinese)

[6] Dai N,Vafidis A,Kanasewich E R.Wave propagation in heterogeneous,porousmedia:a velocity-stress,finite-differencemethod [J].Geophysics,1995,60(2):327-340.

[7] Zeng Y Q,He JQ,Liu Q H.The application of the perfectly matched layer in numericalmodeling of wave propagation in poroelastic media[J].Geophysics,2001,66(4):1258-1266.

[8] 董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):411-419.

DONG Liang-guo,MA Zai-tian,CAO Jing-zhong.A staggeredgrid high-order difference method of first-order elastic equation [J].Chinese Journal of Geophysics,2000,43(3):411-419. (in Chinese)

[9] Collino F,Sogka T.Application of the perfectly matched absorbing layermodel to the linear elasto-dynamic problem in anisotropic hetero-geneousmedia[J].Geophysics,2001,66(1):294-307.

[10] Bouzidi Y.The acoustic reflectivity and transmissivity of liquid saturated Porousmedia:experimental tests of the theoretical concepts[D].Edmonton:University of Alberta,2003.

[11] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid(Ⅰ):low-frequency range[J].JAcoust Soc Am,1956,28:168-178.

[12] Jensen F B,Kuperman W A,Porter M B.Computational ocean acoustics[M].New York:AIP Press,1993.

[13] 李整林,王耀俊,马力.海底沉积物参数对浅海中低频声传播的影响[J].声学学报,2000,25(3):242-247.

LIZheng-lin,WANG Yao-jun,MA Li.Effects of sediment parameters on the low frequency acoustic wave propagation in shallow water[J].Acta Acustica,2000,25(3):242-247.(in Chinese)

A Numerical Simulation of Seism ic W ave Caused by Low Frequency Sound Source in Shallow Sea w ith Thick Porous Sediment by Staggered-grid Finite Difference M ethod

LU Zai-hua,ZHANG Zhi-hong,GU Jian-nong
(College of Science,Naval University of Engineering,Wuhan 430033,Hubei,China)

Elastic wave in the seabed caused by low frequency noise radiated from ship is the so-called ship seismic wave which can be used to identify ship target.In order to obtain the propagation characteristics of ship seismic wave in shallow seawith thick porous sediment,a 3D staggered grid finite difference algorithm for calculating seismic wave at seafloor is presented based on Biotwave theory for porous elastic sediment.Numerical calculation of seismic wave caused by low frequency sound source in a typical shallow sea environment is carried out.The calculated results show that the components of seismic wave in the near field include not only fast P-wave,slow P-wave and S-wave transmitted into the sediment,but also an interface wave which propagates nearby the seafloor.However in the far field,the wave components of seismic wave aremainly normalmodes and interface wave,the former propagatesmainly in the waveguide of sea water and the latter propagates along the seafloor.

vibration and wave;porous sediment;low frequency;shallow sea;seismic wave;staggered grid

P733.23

A

1000-1093(2014)12-2065-07

10.3969/j.issn.1000-1093.2014.12.019

2014-02-24

国家自然科学基金项目(51179195);国防基金项目(513030203-02)

卢再华(1972—),男,副教授,硕士生导师。E-mail:luzaihua01@163.com