随机噪声模拟下机构部件磨损动态可靠性模型及其求解方法

张峰,南华,2,姚会举,3,吕程诚

(1.西北工业大学力学与土木建筑学院飞行器可靠性工程研究所,陕西西安 710129;

2.兰州万里航空机电有限责任公司,甘肃兰州 730700;3.江南机电设计研究所,贵州贵阳 550009)

随机噪声模拟下机构部件磨损动态可靠性模型及其求解方法

张峰1,南华1,2,姚会举1,3,吕程诚1

(1.西北工业大学力学与土木建筑学院飞行器可靠性工程研究所,陕西西安 710129;

2.兰州万里航空机电有限责任公司,甘肃兰州 730700;3.江南机电设计研究所,贵州贵阳 550009)

基于随机动力学理论,开展机构部件磨损动态可靠性的建模,推导了失效概率的求解方法。在机构部件传统磨损分析的基础上,引入白噪声、OU色噪声两种不同类型的随机项来模拟部件磨损过程的动态性和随机性,并以部件动态磨损量和容许磨损量建立磨损动态可靠性模型,推导了动态可靠性基于随机模拟方法和随机泰勒展开方法的求解公式。以某型飞机货桥锁机构为例开展部件磨损动态可靠性分析,验证了所提模型和方法的合理性。

概率论；机构；磨损；随机噪声；动态可靠性；失效概率

0 引言

磨损是机构部件最为突出的失效模式之一。统计表明,机械设备70%的损坏是由磨损引起的,轻者导致机构定位不准确,重者使构件强度不足而发生断裂。因此,对机构部件开展磨损可靠性分析具有极为重要的意义[1]。目前,在机构部件磨损的仿真分析和寿命预测上已有较为深入的研究[2-6]。文献[3-4]以试验为基础建立了机构部件磨损量的估算模型。由于机械产品高可靠性和长寿命,很难通过寿命试验或加速寿命试验的方法来获取部件磨损的失效时间,这限制了以产品失效数据为基础的传统可靠性分析理论的应用。文献[5-6]结合有限元方法开展部件磨损的模拟仿真,并进行磨损寿命预测。文献[7]研究了部件磨损量与载荷、材料特性、磨损作用下的运行距离、表面质量及润滑特性因素的函数关系,建立了部件磨损的可靠性模型。文献[8]基于鞍点逼近法开展了陶瓷刀具磨损寿命可靠性分析。需要指出的是,机构部件稳定磨损过程同时具有动态性和随机性[9],部件的磨损量是个随机过程,需要研究其随时间的演变规律[10]。

综上所述,本文在传统磨损分析的基础上,通过引入随机项来描述磨损过程的动态性和随机性,以部件动态磨损量和容许磨损量建立机构部件的磨损动态可靠性模型,并结合传统可靠性分析的Monte Carlo方法,推导了随机项分别为白噪声和OU色噪声时磨损可靠性基于随机欧拉方法和随机泰勒展开方法的求解流程。最后以某型飞机货桥锁机构部件为例进行机构部件磨损动态可靠性的分析应用。

1 机构部件磨损的动态可靠性模型

在机构部件稳定磨损阶段,磨损量随时间呈线性关系,可以建立如(1)式所示函数关系。

式中:k为磨损速率。

t时间部件磨损量y(t)可以表示为

考虑机构运行过程的动态性和随机性对部件磨损量的影响,并通过随机噪声项ε(t)来模拟实现, ε(t)模拟了部件磨损速率的波动性。此时,部件动态磨损量y(t)与时间t的函数关系,根据(1)式可以表示为

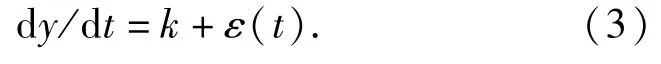
当随机项ε(t)是白噪声时,随机项ε(t)满足[11]

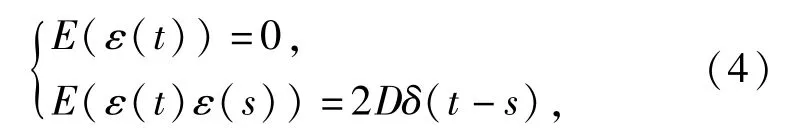
式中:D为白噪声的强度;E(·)表示取数学期望; ε(t)和ε(s)分别为t和s时刻的随机力;白噪声的关联函数δ满足

当随机项ε(t)是OU色噪声时,随机项ε(t)满足[12]

式中:{…}代表对噪声变量的初始值求平均;τc为关联时间。

随机项ε(t)模拟了机构运行过程的动态性和随机性,这表明机构动态磨损量y是个随机过程,需要在传统可靠性的基础上针对部件磨损问题开展动态可靠性分析。设机构部件容许磨损量为y*,根据应力-强度干涉理论建立部件磨损失效的动态可靠性模型,其功能函数g(y)为

式中:g(y)＞0表明机构部件[0,t]时段安全运行;否则,部件磨损量过大会导致机构发生故障。由此可以写出机构部件磨损的失效域F和失效概率Pf为

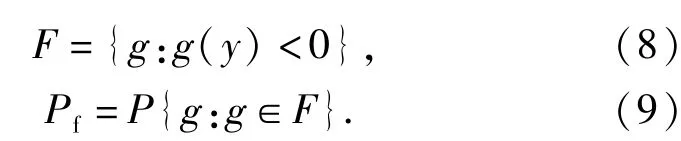
根据大数定律,失效概率Pf基于Monte Carlo方法的无偏估计值为

2 机构部件动态磨损可靠性的求解方法

从(7)式～(10)式可以看出,机构部件动态可靠性求解的关键是在Monte Carlo模拟的同时并对t时段机构部件实际磨损量y(t)进行求解。从(3)式可以看出,部件磨损量y(t)是磨损速率k和随机项ε(t)在[0,t]时段上累积作用的结果,可以通过数值插值方法建立迭代公式来获得。因此,部件磨损动态可靠性的求解是数字模拟方法和数值插值方法有机融合的结果。

2.1 白噪声模拟下磨损动态可靠性分析

当随机项ε(t)是满足(4)式的白噪声时,对(3)式两边进行斯特林积分,可以得到[13]

综合(10)式的Monte Carlo法以及(15)式的欧拉迭代格式,形成了机构部件磨损失效概率求解的随机欧拉方法,其计算步骤如下:

1)将时间段[0,t]等距离离散成n段,步长Δt= t/n;

2)第j(j=1,2,3,…)次模拟。

基于随机欧拉方法求解机构部件磨损失效概率的流程如图1所示。

2.2 OU色噪声模拟下磨损动态可靠性分析

白噪声是一种理想化的模型,而实际的噪声都是色噪声,OU噪声就是一种较好的色噪声模型。用白噪声ζ(t)驱动(16)式所示的线性方程[14]。

式中:ζ(t)满足E(ζ(t))=0,E(ζ(t)ζ(s))=δ(ts).(16)式的解变量就是满足(6)式的色噪声, (16)式的解可写为

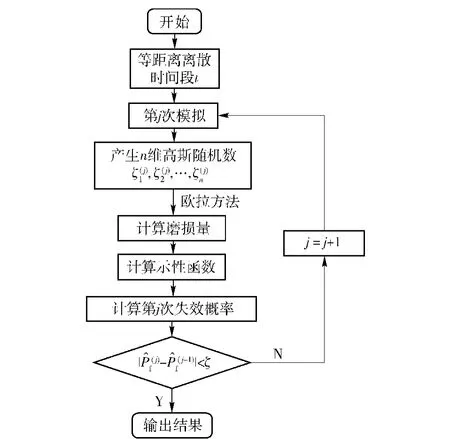
图1 随机欧拉方法流程图Fig.1 Flowchart of stochastic Eulermethod

综合(10)式的Monte Carlo法以及(23)式所示的泰勒展开迭代格式,形成了机构部件磨损失效概率求解的随机泰勒展开方法,其计算步骤如下:

1)将时间段[0,t]等距离离散成n段,步长Δt= t/n;

2)第j(j=1,2,3,…)次模拟。

基于随机泰勒展开方法求解机构部件磨损失效概率的流程如图2所示。

3 算例分析

某型飞机货桥锁机构相对原型机作了重大设计改进,该型货桥锁机构设计的成败直接影响整机的研制质量,需要对货桥锁机构部件开展磨损动态可靠性分析[15]。

锁机构部件容许的磨损量y*=0.75 mm,根据应力-强度干涉模型建立货桥锁机构部件磨损动态可靠性模型,其功能函数g(y)为

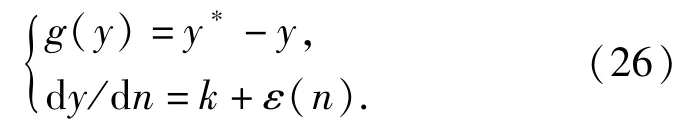
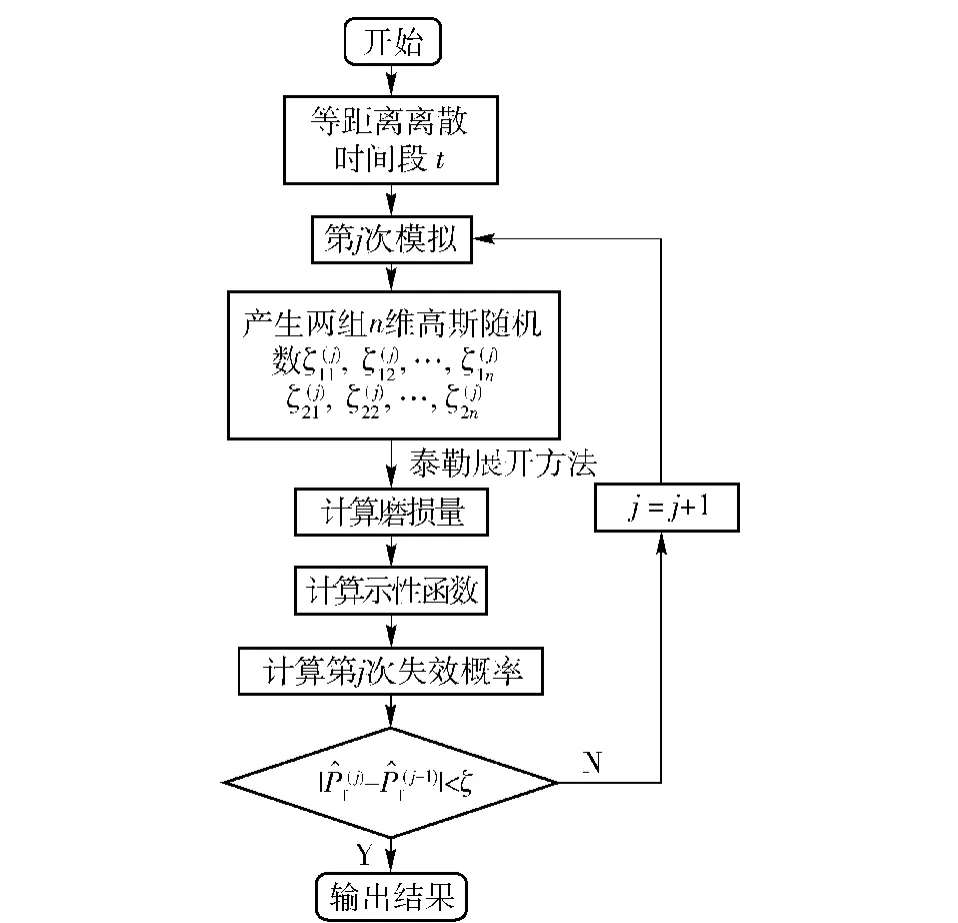
图2 随机泰勒展开方法流程图Fig.2 Flowchart of stochastic Taylor expansion method

锁机构部件处于稳定磨损阶段,磨损速率k= 8.5×10-5mm/次表征了货桥锁机构每次开锁上锁过程的磨损量,ε(n)为随机项,描述了锁机构部件在开锁和上锁过程中的随机性,其相关参数如表1所示。

表1 随机项的相关参数Tab.1 The related parameters of stochastic items

研究5种随机噪声货桥锁机构部件磨损动态可靠性,失效概率通过随机欧拉方法和随机泰勒展开方法求解获得,样本量为105,失效概率估计值的变异系数小于0.1,满足精度要求。失效概率的估算结果如表2所示。

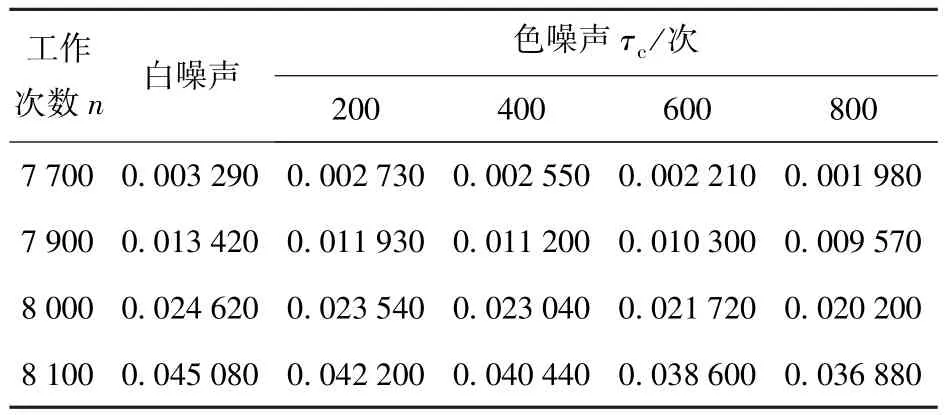
表2 货桥锁机构磨损失效概率Tab.2 The wear failure probability of carbo bridge lock mechanism

图3给出了随机项在4种工作次数下部件磨损失效概率随关联时间变化的规律图。τc=0为随机项白噪声时的结果。

图3 失效概率随关联时间τc的变化关系Fig.3 The relationship between failure probability and correlation time

从图3可以得到以下3点结论:

1)货桥锁机构开锁、上锁工作次数n相同的时候,部件磨损失效概率随关联时间的增加而变小;

2)τc→0,随机噪声项是白噪声时,部件磨损失效概率最大;

3)当关联时间相同时,部件失效概率随锁机构开锁、上锁工作次数n急剧增大。

4 结论

本文建立了机构部件磨损的动态可靠性模型,推导了随机项为白噪声和OU色噪声时机构磨损失效概率求解的随机欧拉方法和随机泰勒展开方法,并以某型飞机货桥锁机构为例进行了可靠性分析。算例验证了所提随机欧拉方法和随机泰勒展开方法在白噪声、OU色噪声模拟机构部件磨损动态可靠性分析中的可行性。

References)

[1] 温诗铸.我国摩擦学研究的现状和发展[J].机械工程学报, 2004,40(11):1-6.

WEN Shi-zhu.Existing state and developmentof tribology research in China[J].Chinese Journal ofMechanical Engineering,2004, 40(11):1-6.(in Chinese)

[2] Gagg C R,Lewis PR.Wear as a product failuremechanism-overview and case studies[J].Engineering Failure Analysis,2007, 14(8):1618-1640.

[3] Andersson J,Almqvist A,Larsson R.Numerical simulation of a wear experiment[J].Wear,2011,271(11):2947-2952.

[4] 杨洪刚,李曙,刘阳,等.有限元模拟TiN膜/碳钢基材体系的摩擦磨损试验[J].摩擦学学报,2009,29(4):293-298.

YANG Hong-gang,LIShu,LIU Yang,et al.Finite element simulation of friction and wear experiment on TiN film carbon/steel substrate system[J].Tribology,2009,29(4):293-298.(in Chinese)

[5] Jiang Q Y,Ge Z L.Simulation on topography of superfinished roller surfaces[J].Science in China Series B:Chemistry,2002, 45(2):122-126.

[6] 江亲瑜,易风,李玉光,等.铰链机构磨损的数值仿真[J].中国机械工程,2005,16(2):100-103.

JIANG Qin-yu,YI Feng,LIYu-guang,et al.Numerical simulation on mild wear of hinge configurations[J].China Mechanical Engineering,2005,16(2):100-103.(in Chinese)

[7] 赵美英,冯元生.机构磨损可靠性高精度算法[J].机械强度, 1998,20(1):49-52.

ZHAOMei-ying,FENG Yuan-sheng.The computation ofwear reliability ofmechanism with high accuracy[J].Journal ofMechanical Strength,1998,20(1):49-52.(in Chinese)

[8] 金雅娟,张义民,张艳林.基于鞍点逼近的陶瓷刀具磨损寿命可靠性分析[J].中国机械工程,2010,21(12):1462-1465.

JIN Ya-juan,ZHANG Yi-min,ZHANG Yan-lin.Reliability analysis of alumina-based ceramic cutting tool'swear life by saddlepoint approximation[J].China Mechanical Engineering,2010,21(12): 1462-1465.(in Chinese)

[9] Kharoufeh JP,Sipe JA.Evaluating failure time probabilities for a Markovian wear process[J].Computers&Operations Research, 2005,32(5):1131-1145.

[10] 刘勤,李娟,刘英.磨损随机过程建模及实例分析[J].兵工学报,2010,31(10):1379-1382.

LIU Qin,LIJuan,LIU Ying.Modeling and example analysis of wear random process[J].Acta Armamentarii.2010,31(10): 1379-1382.(in Chinese)

[11] Higham D J.An algorithmic introduction to numerical simulation of stochastic differential equations[J].Slam Review,2001,43(3): 525-546.

[12] Rubenthaler S.Numerical simulation of the solution of a stochastic differential equation driven by a Lévy process[J].Stochastic Processes and Their Applications,2003,103(2):311-349.

[13] 张晓燕,徐伟,周丙常.色高斯噪声驱动双稳系统的多重随机共振研究[J].物理学报,2011,60(6):162-167.

ZHANG Xiao-yan,XU Wei,ZHOU Bing-chang.Effect of Gaussian color-correlated colored noise on stochastic multiresonance of a bistable system[J].Acta Physica Sinica,2011,60(6): 162-167.(in Chinese)

[14] 包景东.经典和量子耗散系统的随机模拟方法[M],北京:科学出版社,2009.

BAO Jing-dong.Stochastic simulation methods for classical and quantum dissipation systems[M],Beijing:Science Press,2009. (in Chinese)

[15] 喻天翔.机械产品可靠性试验方法研究与应用[D].西安:西北工业大学,2007.

YU Tian-xiang.Research and application on reliability testing for mechanical product[D].Xi'an:Northwestern Polytechnical University,2007.(in Chinese)

Analysis of Dynam ic W ear Reliability of M echanism under Stochastic Noise

ZHANG Feng1,NAN Hua1,2,YAO Hui-ju1,3,LYU Cheng-cheng1
(1.Institute of Aircraft Reliability Engineering,School of Mechanics,Civil Engineering and Architecture, Northwestern Polytechnical University,Xi'an 710129,Shaanxi,China;
2.Lanzhou Wanli Electro-mechanical Inc,Lanzhou 730700,Gansu,China;
3.Jiangnan Institute of Electrical and Mechanical Design,Guiyang 550009,Guizhou,China)

A dynamic wear reliabilitymodel for amechanism is established based on stochastic dynamics theory and the failure probability is estimated.On the basis of traditionalwear analysis,the slochastic items of white and color noises are used to simulate the dymanic nature and randomness ofwear process, and then a limit state function is established by the fact that the dynamic wear loss does notexceed the allowable value.The solving equations of dynamic reliability based on stochastic simulationmethod and stochastic Taylor expansion method are derived.The proposed method is employed to analyze the dynamic wear reliability of an aircraft cargo bridge and verify the reasonableness of themodel and methods.

probability theory;mechanism;wear;stochastic noise;dynamic reliability;failure probability

TB114.3

A

1000-1093(2014)12-2104-05

10.3969/j.issn.1000-1093.2014.12.025

2014-02-18

高等学校博士学科点专项科研基金项目(20136102120032),高等学校学科创新引智计划项目(B07050),西北工业大学基础研究基金项目(JC20100232)

张峰(1982—),男,副教授。E-mail:nwpuwindy@mail.nwpu.edu.cn