改进的离散小波-优化极限学习机在倾转旋翼机故障诊断中的应用

严峰,陈晓,王新民,彭程,胡亚洲

(1.中航工业直升机设计研究所,江西景德镇 330001,2.西北工业大学自动化学院,陕西西安 710129)

改进的离散小波-优化极限学习机在倾转旋翼机故障诊断中的应用

严峰1,陈晓2,王新民2,彭程2,胡亚洲2

(1.中航工业直升机设计研究所,江西景德镇 330001,2.西北工业大学自动化学院,陕西西安 710129)

针对倾转旋翼机飞控系统的故障诊断问题,提出一种改进的离散小波-优化极限学习机(OMELM)的故障诊断算法。提出自适应启发式小波去噪方法对采集的信号进行消噪,定义了帕塞瓦尔能量用来提取测量信号经离散小波变换分解后的特征,并对OMELM进行了改进。将提取的故障能量特征进行归一化后输入到改进的OMELM多分类器中进行分类,以美国XV-15倾转旋翼机为例进行仿真验证。结果表明文中方法平均辨识率高,诊断时间短,对未来我国进行倾转旋翼机故障诊断的研究有一定参考价值。

航空、航天系统工程;倾转旋翼机;故障诊断;离散小波;优化极限学习机;自适应启发式小波去噪

0 引言

倾转旋翼机是一种介于直升机、固定翼飞机之间的新构型飞行器,通过机翼两端短舱的倾转,可以在直升机模式和固定翼模式之间进行过渡转换。由于气动布局构型和操纵特性比较复杂,且飞控系统实现了直升机操纵和固定翼操纵的结合,其如果发生故障会对倾转旋翼机的飞行操纵产生较大的影响。因此,开展倾转旋翼机飞控系统的故障诊断研究十分重要。

从20世纪80年代国外开始研发倾转旋翼机以来,到目前为止国内外学者对倾转旋翼机的研究大部分集中在气动力建模[1-4]、飞行控制[5-7]等方面,据文献资料仅有Kim团队在韩国政府的支持下于2012年开始研究倾转旋翼无人机飞控系统的容错控制[8],暂时还没有人涉足倾转旋翼机飞控系统的故障诊断,不过韩国政府对容错控制的关注表明了故障诊断和容错控制是倾转旋翼机未来的研究趋势。

早在20世纪80年代,神经网络开始应用于故障诊断的研究中[9-10],并且越来越得到重视。目前解决飞控系统故障诊断问题最具潜能的方法之一被认为是神经网络[11],并且该方法已在B737和X-36无尾翼飞机上进行了试验验证[12-13],可见神经网络不仅从理论上还是从工程应用方面都引起了人们广泛的关注。然而传统学习算法固有的一些缺点,如训练速度慢、容易陷入局部极小点以及学习速率的选择敏感等成为制约其发展的主要瓶颈。因此,探索一种训练速度快、获得全局最优解,且具有良好的泛化性能的训练算法是近年来的研究热点和难点。

2011年以来,极限学习机(ELM)作为故障诊断领域的一种新方法被国内外学者关注和研究[14]。ELM是Huang等[15]于2006年根据摩尔-彭罗斯(MP)广义逆矩阵理论提出的一种机器学习新算法。后来根据Bartlett[16]理论,Huang等对传统ELM进行改进,提出了优化极限学习机(OMELM)算法[17]。OMELM算法随机地选择输入权值和隐层节点阈值,并且输出权值是在确定的输入权值和隐层节点阈值的基础上求得,因而可能存在一系列并非最佳的输入权值和隐层节点阈值,导致OMELM的分类精度受到影响。

为了提高OMELM的分类精度,本文提出了基于复合混沌的算法来搜索OMELM模型的最佳输入权值及隐层节点阈值。另外从提高时间效率的角度出发,本文定义了帕塞瓦尔能量用来提取测量信号经离散小波变换分解后的特征,最后将归一化后的能量特征向量输入到改进的OMELM网络进行故障类型诊断。

1 倾转旋翼机XV-15的动力学模型

本文以具有机翼、双旋翼、水平尾翼和双垂尾翼布局的美国倾转旋翼机XV-15为研究对象,其气动布局如图1所示。

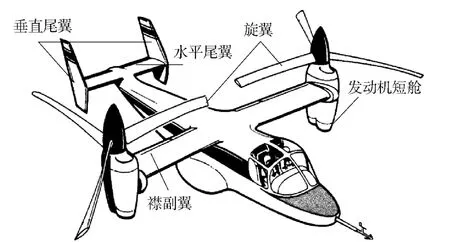
图1 倾转旋翼机XV-15的气动布局示意图Fig.1 Aerodynamic layout of tiltrotor aircraft

倾转旋翼机的6自由度非线性动力学模型描述为

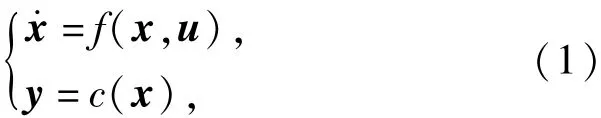
式中:x、u和y分别表示状态向量、控制输入向量和输出向量。

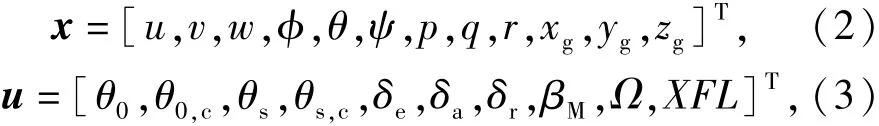
(2)式和(3)式中:[u,v,w]和[p,q,r]分别是飞行速度v和转动角速度ω在机体坐标轴系各轴上的分量;[φ,θ,ψ]是姿态角,即通常所指的欧拉角;[xg, yg,zg]是倾转旋翼机在地面坐标系中的位置;[θ0, θ0,c,θs,θs,c]是总距、差动总距、纵向周期变距和差动纵向周期变距;[δe,δa,δr]是升降舵、襟副翼和方向舵偏角;[βM,Ω,XFL]是发动机短舱倾转角,旋翼转速和襟翼偏转角。

旋翼转速和襟翼偏转角的取值[2]如下:

旋翼转速

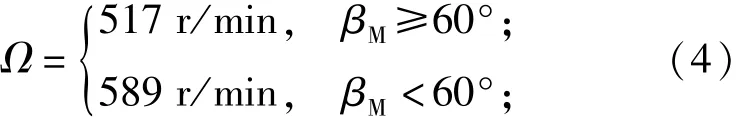
襟翼偏转角

2 改进的离散小波-OMELM方法

2.1 自适应启发式小波去噪

噪声信号通常表现为高频信号,对原信号进行离散小波分解后,噪声部分通常会含在高频分解系数即小波系数中,对高频分解系数以门限阈值等形式进行处理,然后对信号进行重构,就可以达到消除噪声的目的。

假设1w=(w1,…,wN)是用来估计阀值的小波系数向量,向量长度为N.

自适应启发式小波去噪算法如下:

步骤1选定一个合适的小波基与分解层数L,对含噪信号进行离散小波分解。

步骤2对每一层的高频分解系数采用自适应启发式方法进行阈值量化。

阈值量化是影响小波去噪效果的关键,故提出自适应启发式方法选取阀值TR,如下:

步骤2.1计算变量η和κ:

2.2 离散小波故障特征提取

离散小波对去噪信号f(t)的L层分解表示为

2.3 改进的OMELM

与传统的神经网络算法不同,ELM网络的输出权值能以最小化模的方式计算。文献[16]中Bartlett理论指出,前馈型神经网络训练误差较小时,网络输出权值的范数值越小,网络具备的泛化性能就越好。据此,Huang等对传统ELM进行改进,提出了OMELM算法[17]。

基于优化理论,利用代价参数C来平衡最小化输出权值的模‖β‖和最小化训练误差ξi的权重,则OMELM的数学模型可表示为(17)式的形式。

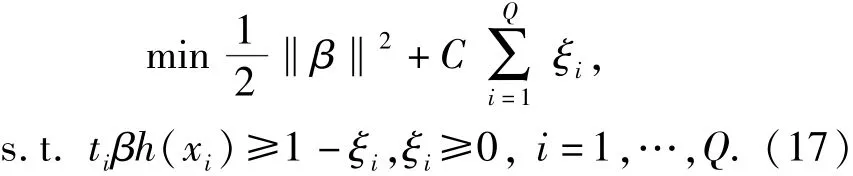
OMELM随机地选择输入权值和隐层节点阈值,并且输出权值是在确定的输入权值和隐层节点阈值的基础上求得,因而可能存在一系列并非最佳的输入权值和隐层节点阈值,导致OMELM的分类精度受到影响。混沌运动具有遍历性、随机性和规律性的特点,同遗传算法等随机搜索算法相比,更适合用于学习模型的优化。为了提高OMELM的分类精度,本文提出基于复合混沌的算法来搜索OMELM模型的最佳输入权值及隐层节点阈值。

定义2 称(18)式

3 基于改进的离散小波-OMELM的故障诊断算法

4 仿真实验结果与分析

仿真实验是在IBM计算机(奔腾4,CPU 3.00 GHz,内存2 G)上进行的,编程环境是Matlab R2009a.

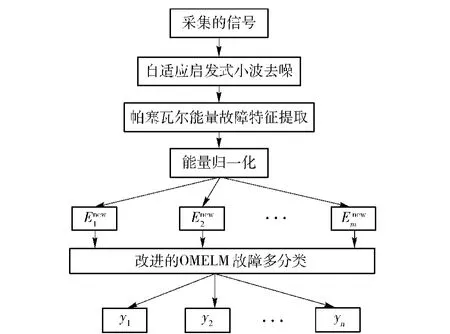
图2 故障诊断系统的结构Fig.2 Fault diagnosis system structure

倾转旋翼机巡航时处于固定翼模式,此时发动机短舱倾转βM=90°,旋翼转速Ω=589 r/min,襟翼偏转角XFL=0°.设计鲁棒PID控制律使倾转旋翼机水平平飞(高度1 800 m,速度80 m/s).图3给出了平飞控制律设计的仿真结构。

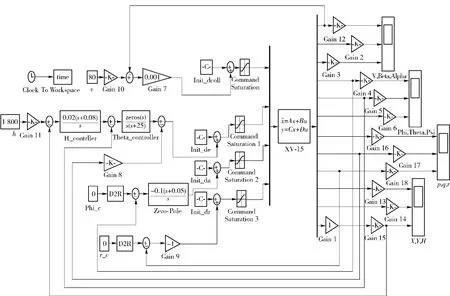
图3 平飞控制律设计仿真结构图Fig.3 Simulation structure of level flight control law design

为了使改进的离散小波-OMEIM诊断效果好,精度高,应该选择故障类型能影响到的,并且容易测量的倾转旋翼机输出信号进行样本采集。执行器发生故障后,选择倾转旋翼机的快变量俯仰角速度作为故障测量信号。图4给出了升降舵卡死在-8°时,俯仰角速度的故障输出情况。

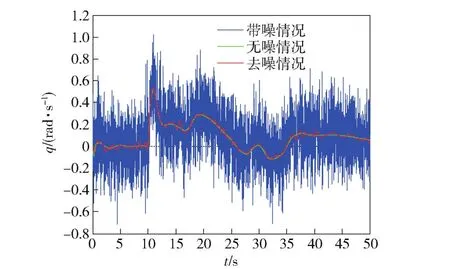
图4 升降舵卡死在-8°时俯仰角速度输出Fig.4 Pitch rate output curve of elevator stuck at-8°

图4中绿色曲线为无噪情况下的信号,蓝色曲线为有噪声情况下的信号,红色曲线为采用2.2节中的自适应启发式小波去噪后的信号。从该图中可以看出,无噪俯仰角速度信号从第10 s开始发生故障,急剧增大;加噪后的情况将卡死之前和之后的俯仰角速度信号微小变化几乎掩盖了;去除噪声之后的曲线变化趋势和原曲线一致,这也说明了自适应启发式小波去噪算法的有效性。

4.1 故障注入及信号采集

执行器故障注入过程如下:预先设定执行器的故障位置和故障时刻,未到达该时刻前系统一直以正常方式运行,到达该时刻后系统输出逐渐偏离正常位置,直至到达并保持在故障位置,即

假设故障发生时间为10～50 s.考虑正常飞行和3种故障类型:升降舵卡死,卡死程度为-8°;升降舵损伤,损伤程度为80%;襟副翼卡死,卡死程度为2°.

对倾转旋翼机的俯仰角速度信号进行采样,设采样周期Ts=12.5 ms,采样间隔10Ts,采样时间T= 16 s,采集的样本点数则为T/(10×Ts)=128.在故障发生后的第1个采样周期开始采集数据,正常飞行和每个故障类型均采集30组样本,为保证分类的准确性,每类随机选择8组作为训练样本,剩下的22组作为测试样本。

4.2 分类结果与分析

离散小波进行变换分解时,分解层数选择5,基小波选择db4[19].图5为采集的俯仰角速度样本信号经过离散小波分解后各层系数的表示曲线。

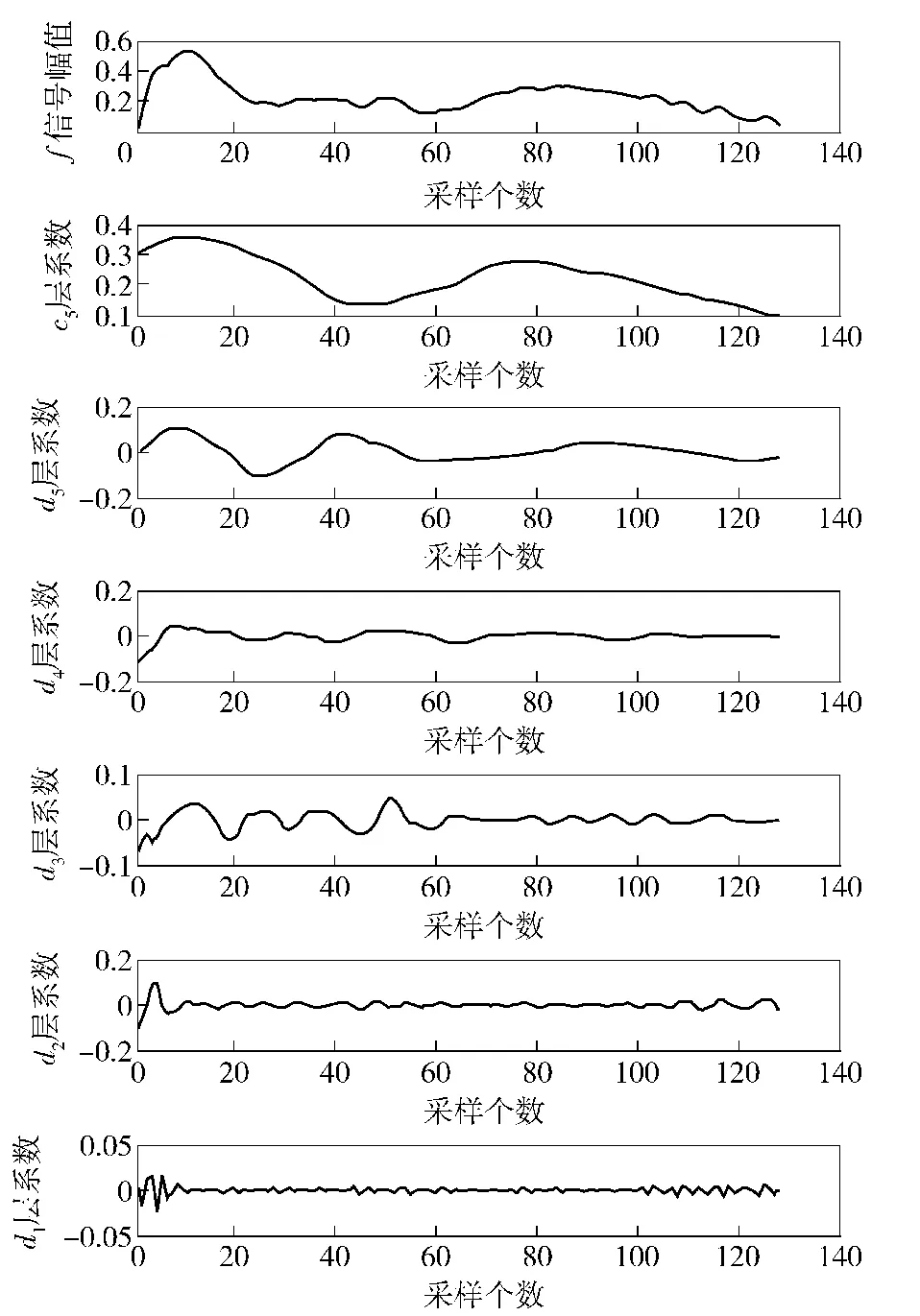
图5 俯仰角速度故障信号去噪后的离散小波分解Fig.5 Discrete wavelet decomposition of pitch rate fault signal after denoising

根据(16)式提取图6小波分解后各层系数的能量特征,按(26)式对特征向量归一化,将归一化后的特征向量输入到改进的OMELM多分类器中进行故障诊断。图6是归一化后的特征向量对应的条形图,从左到右依次表示d1、d2、d3、d4、d5和c5对应的归一化特征向量。

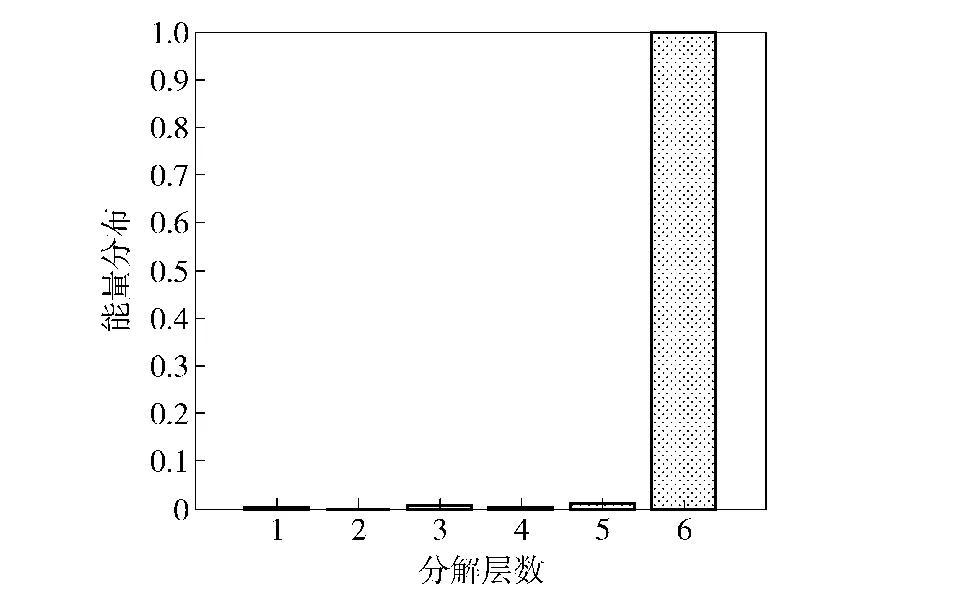
图6 各层系数能量特征的归一化Fig.6 Energy feature normalization of every layer

为了与其他故障诊断算法作比较,采用辨识率r来评价故障诊断的精度:

式中:Nt是每类测试样本数;Nc是每类测试样本中正确诊断的数目。

采用改进的离散小波-OMELM(方法1)和基本的OMELM(方法2)进行故障诊断,诊断结果如表1所示。

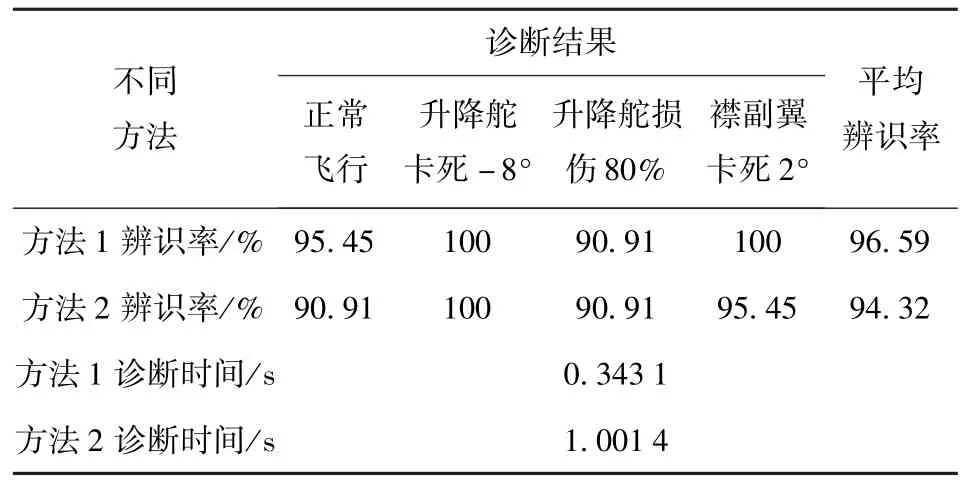
表1 倾转旋翼机执行器故障诊断情况Tab.1 Fault diagnosis of tiltrotor aircraft actuator

表1中诊断时间为训练时间加上测试时间,平均辨识率为测试样本中正确诊断的数目占测试样本总数的百分比。分析表1知:在诊断正常飞行时,方法1(本文方法)的辨识率大于方法2;诊断升降舵和襟副翼卡死时,两种方法的诊断精度都比较高;3种故障类型中,两种方法诊断精度最低的均是升降舵损伤80%。方法1(本文方法)对故障进行诊断的平均辨识率要大于方法2,为96.59%;所需的诊断时间比方法2要短。这是由于经过离散小波特征提取之后的维数(6个)小于基本的OMELM方法的输入特征维数(12个),因此收敛速度比较快。

为了直观地观察、分析结果,这里以图形的形式给出最终的测试集预测结果,如图7所示。

图7为方法1(本文方法)和方法2在22×4= 88组测试集上的测试结果。横轴表示测试样本数,纵轴表示故障模式类别取值,整数1～4分别表示正常飞行、升降舵卡死、升降舵损伤和襟副翼卡死。可以直观地看出本文方法对正常飞行和升降舵损伤80%的样本误判个数分别为1个和2个,方法2对正常飞行、升降舵损伤80%以及襟副翼卡死2°的样本误判个数分别为2个、2个和1个。

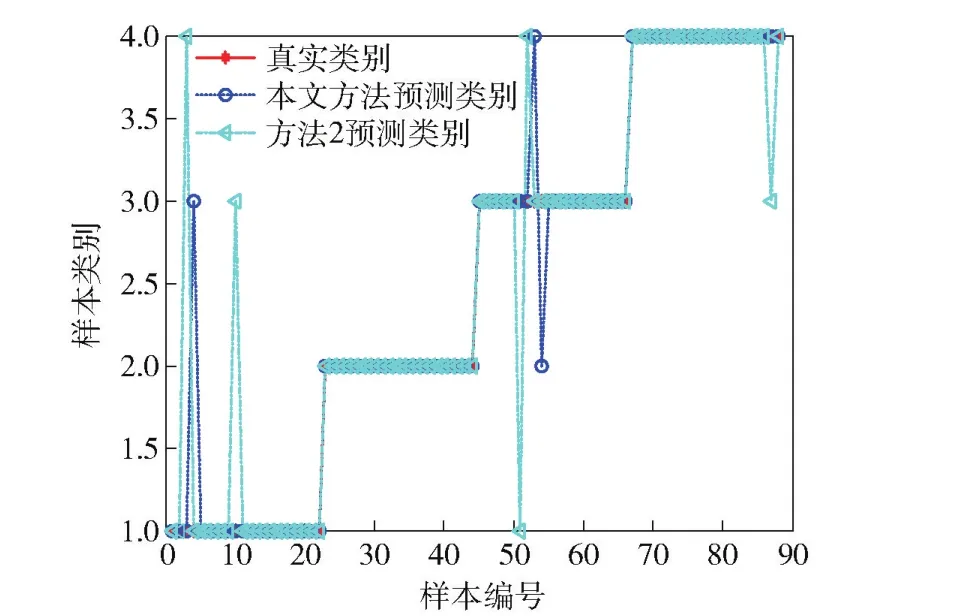
图7 测试集测试结果对比Fig.7 Comparison of test results of test sets

5 结论

本文用自适应启发式小波去噪方法对故障信号进行去噪,然后用定义的帕塞瓦尔能量提取离散小波分解后各层系数的特征,将特征向量归一化后输入到改进的OMELM分类器中进行故障模式的多分类。仿真时分别采用本文方法和基本的OMELM方法进行故障诊断,根据仿真结果得到以下结论:

1)利用本文方法对故障进行诊断时,考虑了实际系统采样时夹杂的噪声影响,并且用离散小波提取的特征维数比基本的OMELM方法要少。

2)本文方法平均辨识率高于基本的OMELM方法,诊断时间小于基本的OMELM方法,因此整体上优于基本的OMELM方法。

倾转旋翼机有旋翼和固定翼两套操纵系统,当它以直升机模式飞行时,参与操纵控制的执行器与固定翼模式下是不一样的,但执行器的故障模型均是一样的,即本文提出的方法实际上对飞机的直升机模式也是有效的。

References)

[1] Ferguson S W.A mathematical model for real time flight simulation of a generic tiltrotor aircraft,NASA CR-166536[R].US: NASA,1988.

[2] Kleinhesselink K M.Stability and control modeling of tiltrotor aircraft[D].Maryland:University of Maryland,2007.

[3] 宋彦国,王焕瑾,沙虹伟,等.倾转旋翼飞行器飞行力学模型研究[J].空气动力学报,2008,26(2):192-196

SONG Yan-guo,WANG Huan-jin,SHA Hong-wei,et al.Flight dynamic mathematical model of tiltrotor aircraft[J].Acta Aerodynamica Sinca,2008,26(2):192-196.(in Chinese)

[4] 周文雅,李立涛,杨涤.倾转旋翼航空器建模方法研究[J].飞行力学,2008,26(3):5-9.

ZHOU Wen-ya,LI Li-tao,YANG Di.Study on tilt rotor aircraft modeling method[J].Flight Dynamics,2008,26(3):5-9.(in Chinese)

[5] Rysdyk R T,Calise A J.Adaptive model inversion flight control for tilt-rotor aircraft[J].Journal of Guidance,Control,and Dynamics,1999,22(3):402-407.

[6] Hathaway E L.Active and passive techniques for tilt rotor[D]. Pennsylvania:the Pennsylvania State University,2010.

[7] 沙虹伟.无人倾转旋翼机飞行力学建模与姿态控制技术研究[D].南京.南京航空航天大学,2007.

SHA Hong-wei.A mathematical model of unmanned tiltrotor aircraft and research on attitude control system design[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.(in Chinese)

[8] Park S,Bae J,Kim Y.Fault tolerant flight control system for the tilt-rotor UAV[J].Journal of the Franklin Institute,2013,350 (9):2535-2559.

[9] Chow M Y,Mangum P,Thomas R J.Incipient fault detection in DC machines using a neural network[C]∥Proceedings of the 22nd Asilomar Conference on Signals,Systems,and Computers. San Jose,US:IEEE,1988:706-709.

[10] 李晗,萧德云.基于数据驱动的故障诊断方法综述[J].控制与决策,2011,26(1):1-9.

LI Han,XIAO De-yun.Survey on data driven fault diagnosis methods[J].Control and Decision,2011,26(1):1-9.(in Chinese)

[11] 谢勇.无人直升机飞行传感器仿真及其故障诊断与容错技术研究[D].南京:南京航空航天大学,2010.

XIE Yong.Research on servo control system of an airborne tracking and stabilization platform[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010.(in Chinese)

[12] Marcello Napolitano,Younghwan An,Brad Seanor,et al.Application of a neural sensor validation scheme to actual Boeing B737 flight data[C]∥Guidance,Navigation and Control Conference and Exhibit.Portland,OR:AIAA,1999:1531-1541.

[13] Brimker J S,Wise K.Flight testing of a reconfigurable control of a tailless fighter aircraft,AIAA-2000-3941[R].US:AIAA, 2000.

[14] 尹刚,张英堂,李志宁,等.基于在线半监督学习的故障诊断方法研究[J].振动工程学报,2012,25(6):637-642.

YIN Gang,ZHANG Ying-tang,LI Zhi-ning,et al.Fault diagnosis method based on online semi-supervised learning[J].Journal of Vibration Engineering,2012,25(6):637-642.(in Chinese)

[15] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine: theory and applications[J].Neurocomputing,2006,70(1): 489-501.

[16] Liang N Y,Huang G B,Saratchandran P,et al.A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks,2006, 17(6):411-1423.

[17] Huang G B,Chen I.Convex incremental extreme learning machine[J].Neurocomputing,2007,70(16/17/18):3056-3062.

[18] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]∥2004 IEEE International Joint Conference on Neual Networks,Vol 2. Budapest,Hungary:IEEE,2004:985-990.

[19] Lang F N,Yuan X,Zhou J L.Redundancy analysis of wavelet transform coefficient[J].Acta Automatica Sinica,2009,33(4): 568-577.

Fault Diagnosis of Tiltrotor Aircraft via Improved Discrete Wavelet-OMELM

YAN Feng1,CHEN Xiao2,WANG Xin-min2,PENG Cheng2,HU Ya-zhou2
(1.AVIC China Helicopter Research and Development Institute,Jingdezhen 330001,Jiangxi,China;
2.School of Automation,Northwestern Polytechnical University,Xi'an 710129,Shaanxi,China)

An improved discrete wavelet-optimization method-based extreme learning machine(OMELM) algorithm is presented for the fault diagnosis of flight control system in tiltrotor aircraft.An adaptive heuristic wavelet denoising method is used to denoise the sampled signal.Feature vector of each layer is extracted using Parseval energy after the discrete wavelet decomposition of fault signal.The energy feature is normalized as the improved OMELM network input,and then the actuator fault models is classified using the improved OMELM network.Finally,an XV-15 tiltrotor aircraft mode is validated by simulation.The results show that the method has a higher average recognition rate,and needs a short diagnosis time.

aerospace system engineering;tiltrotor aircraft;fault diagnosis;discrete wavelet transform; optimization method-based extreme learning machine;adaptive heuristic wavelet denoising

V275+.1

A

1000-1093(2014)11-1914-08

10.3969/j.issn.1000-1093.2014.11.025

2013-11-24

严峰(1978—),男,高级工程师。E-mail:123683941@qq.com;

陈晓(1982—),女,博士研究生。E-mail:candychch@mail.nwpu.edu.cn