耦合尾喷管堵盖运动的发射箱内流场研究

于邵祯,姜毅,周笑飞,牛钰森,孙璐璐

(1.北京理工大学宇航学院,北京 100081;2.海军航空工程学院青岛校区,山东青岛 266041)

耦合尾喷管堵盖运动的发射箱内流场研究

于邵祯1,姜毅1,周笑飞1,牛钰森1,孙璐璐2

(1.北京理工大学宇航学院,北京 100081;2.海军航空工程学院青岛校区,山东青岛 266041)

利用初始冲击波超压完成前后盖开启过程的贮运发射箱已得到广泛应用。为研究含尾喷管堵盖的冲击波超压形成过程及对后易碎盖的作用效果,应用有限元方法并结合动网格技术建立了导弹点火后堵盖的运动模型,并通过实验方法对仿真结果进行了验证。结合计算结果可清晰地看到尾焰流场的形成过程,并得到了冲击波超压在后易碎盖表面的随时间变化曲线。研究表明:受堵盖的影响,冲击波超压首先形成并冲击后易碎盖,燃气由堵盖的边缘向中心汇聚形成主流,在对后易碎盖的冲击时间和作用位置上与冲击波作用有明显的不同;后易碎盖主要受到冲击波超压作用实现碎裂变形,在堵盖运动的投影区域首先达到最大受力,瞬时峰值达5×105Pa.

兵器科学与技术;尾喷管堵盖;冲击波;易碎盖;数值仿真

0 引言

冲击波开盖技术在目前应用广泛并日臻成熟。发射箱内冲击波的形成是导弹在箱内点火后,高压燃气流从喷管喷出与周围空气形成最初的压力界面,并以同射流边界大致近似的形状随着燃气流向外发展而向前推进,同时伴随能量不断增强[1]。冲击波开盖技术是利用冲击波能量实现对设计有一定承压标准的易碎盖的开启[2]。利用冲击波开盖技术的贮运发射箱结构简单,质量轻,操作维护方便,经济成本较低,因此有广阔的应用前景。

箱体前后易碎盖的压力匹配问题是采用易碎盖技术亟待解决的问题之一,前后易碎盖的强度设计标准与冲击波的强度密切相关。冲击波在形成过程中受到箱内配件如导轨、扰流器、堵盖等影响。在诸多影响因素中,尾喷管堵盖对箱内射流形状和冲击波的形成及强度影响较大,而对于某些型号的导弹发动机来说,尾喷管堵盖安放有点火器并起到射前增压的作用[3],为导弹必不可少配件,因此有必要考虑有堵盖影响的发射箱内冲击波的形成过程。

对于易碎盖技术的研究,国外起步较早,并且已经有成熟的应用,如美国的“陆麻雀”、“爱国者”“战斧”,意大利的“阿斯派德”、“信天翁”等,同时对于超音速流产生的冲击波在能量、成因以及数值模拟方法和实验的研究上取得了很大的进展[4-6]。国内对于箱内冲击波的研究主要集中在冲击波形成后在箱内的传播过程,分析过程以实验并辅助工程经验为主[7-11],也取得了一定的研究成果,对于冲击波在发射箱内部的作用效果也有了一定的认识,但是目前对于利用冲击波能量完成开盖动作的发射箱设计主要以工程经验为主,对于冲击波的强度分析只能预估在一定的范围内,不能进行定量分析,严重影响了易碎盖的设计精度和使用的可靠性。

本文通过数值仿真计算模拟了尾喷管堵盖在箱体内受到燃气流作用的运动过程,并通过监测发射箱后易碎盖的平均静压研究冲击波作用力的变化过程,同时根据实验结果对冲击波作用效果进行验证,为贮运发射箱易碎盖设计提供参考。

1 基本控制方程

燃气射流的控制方程组采用三维非定常方程组[12]。湍流方程采用标准k-ε模型方程(具体方程见文献[12])。

湍动能k的输运方程为

式中:μt为湍流粘性系数;Gk为由层流速度梯度产生的湍流动能;Gb为由浮力产生的湍流动能;C1ε、C2ε、C3ε、σk、σε为经验常数;Cμ为湍流常数。

在动网格计算区域内,在任意控制体V中任意标量的积分形式的控制方程可以表示为

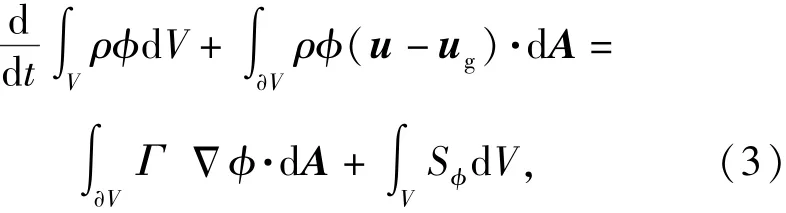
式中:ρ表示流体密度;φ为通量变量;u表示流体速度矢量;ug表示动网格运动速度;Γ表示耗散系数; Sφ表示源项。

2 计算实例

2.1 计算模型

仿真模型模拟发射箱内导弹点火时刻尾喷管堵盖从初始位置运动到后易碎盖端面过程。计算模型包括发射箱箱体、前后导轨、导弹弹体、发动机喷管、堵盖在内的三维模型。模型中根据堵盖的设计外形将堵盖简化处理为圆形薄片,并将原堵盖质量均匀加载。计算区域如图2所示。由于堵盖运动行程短,速度大,同时导弹的发射姿态以倾斜和垂直发射为主,因此将堵盖的运动轨迹按照直线形式处理。模型中取堵盖面向发射箱前易碎盖端面为前端面,反向为后端面。计算模型根据对称性采用1/2模型计算。

模型网格划分如图2所示,采用6面体结构化网格,对于喷管区域采用加密处理,同时设置堵盖运动区域的边界面为Interface边界,在Interface边界的两侧采用等比例网格尺寸划分,其网格高度为0.5 mm,比例系数为1.2,如图2所示。网格总数为40万。

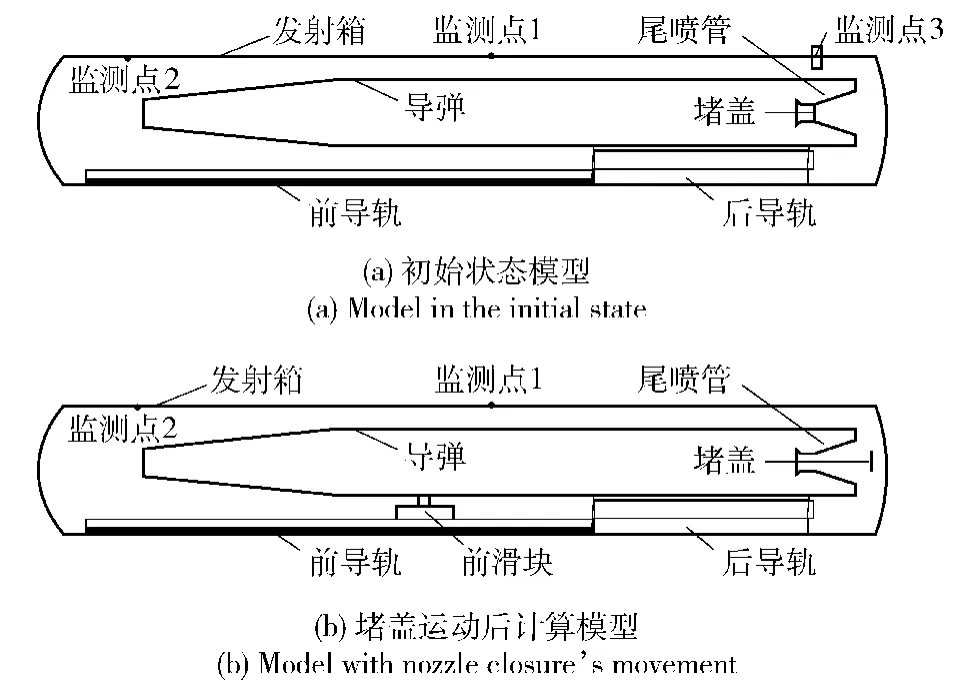
图1 仿真计算物理模型Fig.1 The physical model for simulation calculation

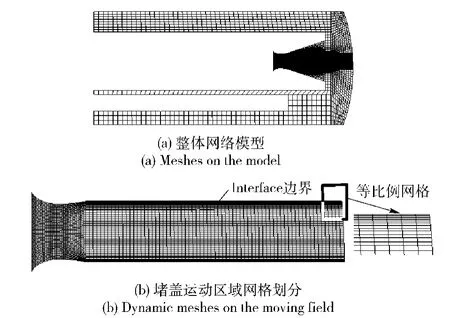
图2 计算网格模型Fig.2 Mesh model

2.2 计算条件

如图3所示,对实验所测得的发动机压力变化曲线进行数值离散处理并拟合出发动机燃烧室内压强变化方程,假设总温变化在点火初始状态至发动机工作稳定时刻为线性变化,将总温与总压变化曲线编写自定义函数输入到仿真计算中。

计算使用Fluent软件,应用有限体积法。对弹体、导轨、喷管及发射箱等固壁表面采用标准壁面函数方程处理。堵盖的运动速度为自定义函数:通过读取堵盖两侧的压强分布并积分转换成作用力加载在堵盖表面进行计算。根据实验测得的破膜压力为1.5 MPa,因此仿真计算中将燃烧室压力达到1.5 MPa时刻设置为堵盖运动初始时刻。

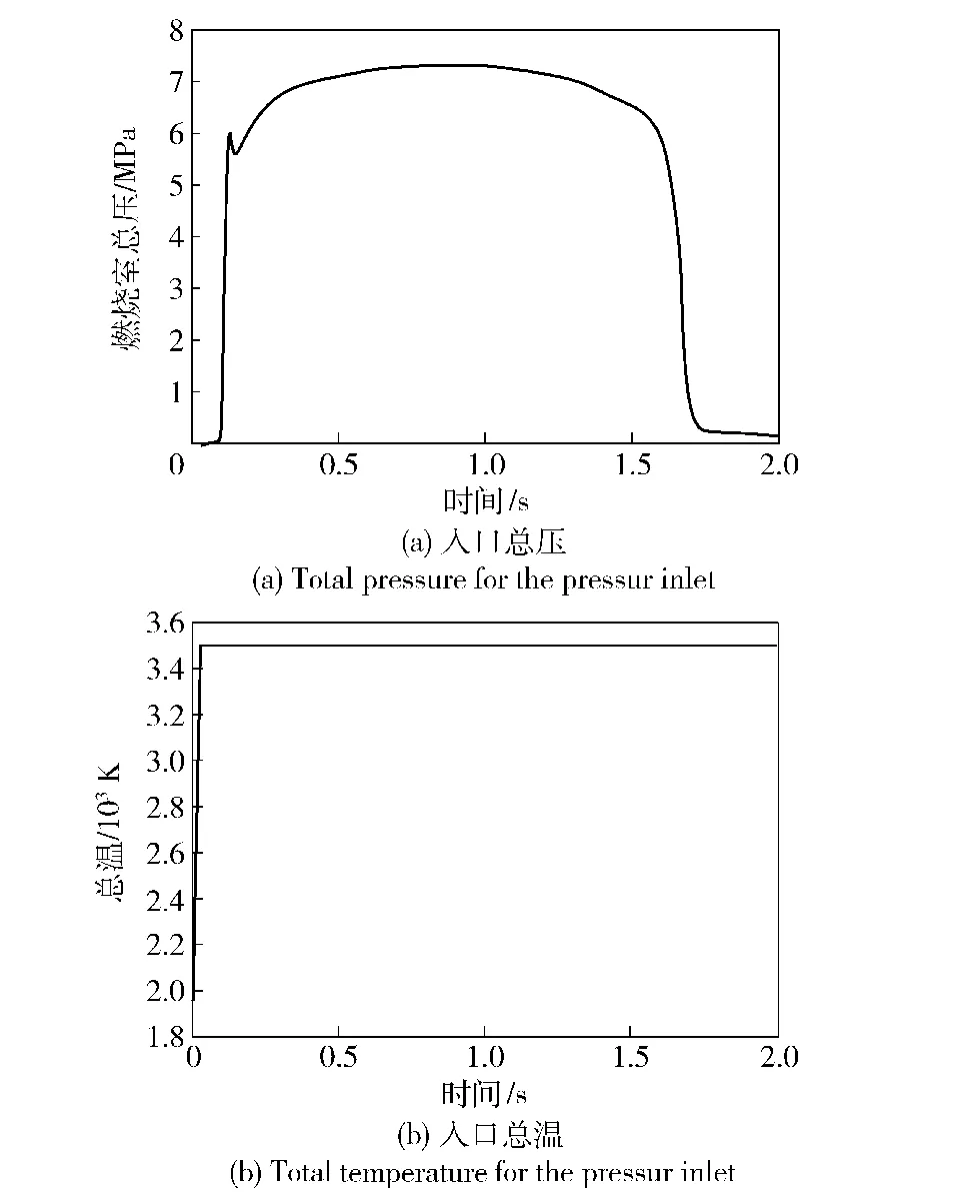
图3 压力入口边界条件Fig.3 Boundary conditions on the pressure inlet

2.3 数值计算验证

模拟实验可有效检验数值计算结果的精度和可靠性,但是在实验中不能直接对堵盖的运动状态和受到的作用力进行测量。而发射箱后盖采用易碎盖设计,同样不能直接获取后盖的受力情况。因此只能通过对其他相关数据进行测量对比进行间接验证。发动机点火后在发射箱内形成的初始冲击波超压是与燃气流特性最相关的物理量,利用压力传感器可直接对超压值进行测量,如图1所示的发射箱模型,实验中在发射箱壁面上设置监测点1、2两个压力监测点对发射箱内冲击波数据采集。

图4所示为发动机点火后发射箱内冲击波的传播过程。白色区域为冲击波超压值影响区域,从图4中可以看出发射箱内初始冲击波超压值接近170 000 Pa,并且波前和波后超压值有明显的阶跃,因此在实验中能够对冲击波流经监测点处的作用时长和峰值进行监测并获得相关数据。

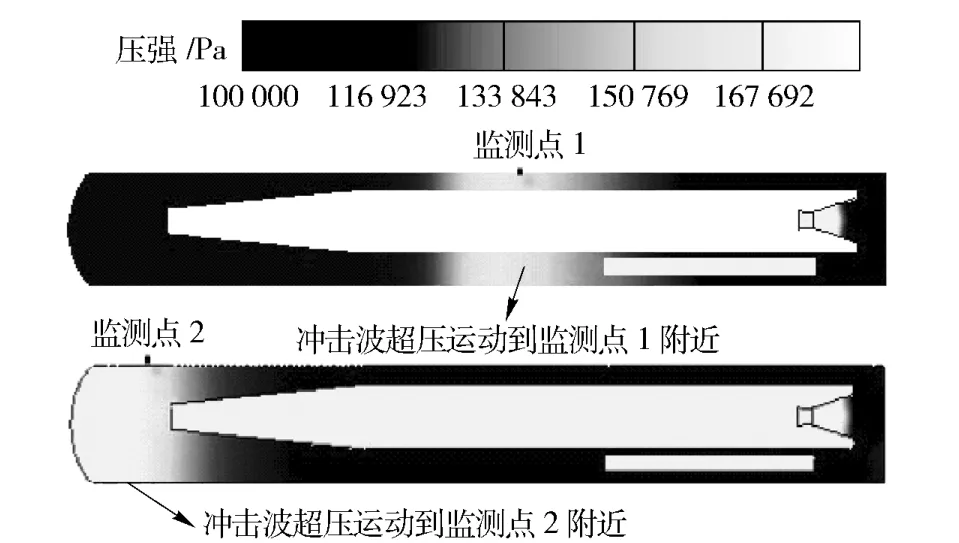
图4 初始冲击波传播过程Fig.4 The propagation of initial shock wave

图5为冲击波流经监测点处的超压变化曲线,需要说明的是实验过程中前易碎盖的开启是利用多组冲击波的积聚达到一定强度后实现。因此对于初始冲击波在监测点处的传播历程由于反射作用会出现多次峰值,实验曲线如图5(a)所示。在监测点1、2中,监测点1的初始峰值出现时间要早于监测点2,而第2个峰值出现时间在监测点2第2个峰值之后,有力的证明了冲击波的反射结论。而仿真计算只记录了发射箱首次传播过程,因此在进行数据对比中只对冲击波第1个峰值大小和时程进行对比。另外由于时间基准在实验和数值计算中很难统一,在图5(b)和图5(c)的压强变化曲线中选取峰值点时刻作为基准进行对比分析。由监测点的压强变化曲线可知实测值与计算值压强变化在时间跨度和峰值上都比较接近。从表1中数据对比可知,监测点理论计算强度和实测值误差最大为4.51%.在时间历程上二者误差最大为33.30%.而堵盖与燃气流耦合作用主要受强度因素的影响,因此数值计算满足精度要求。

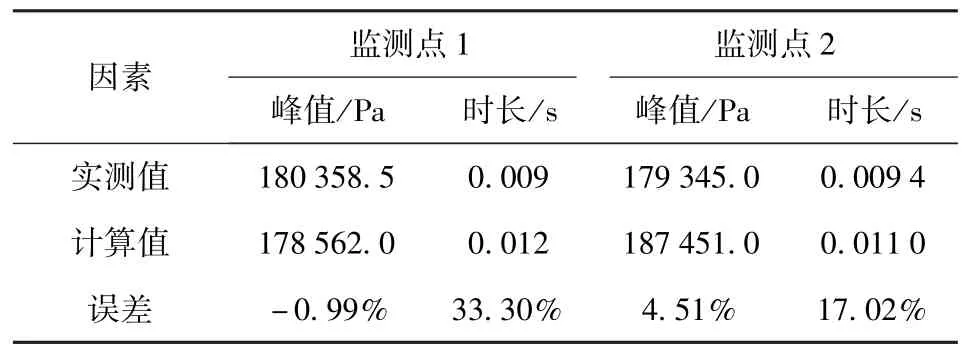
表1 监测点压强数据对比Tab.1 Comparison of pressure data

3 计算结果分析

3.1 仿真云图分析

图6所示为堵盖运动0.5 ms时刻燃气流从堵盖与喷管间隙流出的仿真云图。图6(a)所示为对称面燃气流静压云图,可以清晰地看到堵盖周围的燃气压强紧贴壁面处发生变化,燃气流从喷管与堵盖间隙流出后由边界向堵盖中心扩散。图6(b)所示为喷管内温度云图,燃气流开始沿管壁向外扩散,在此状态下,燃气流温度分布与压强分布一致。发射箱易碎盖上暂未受到燃气流扰动的影响。

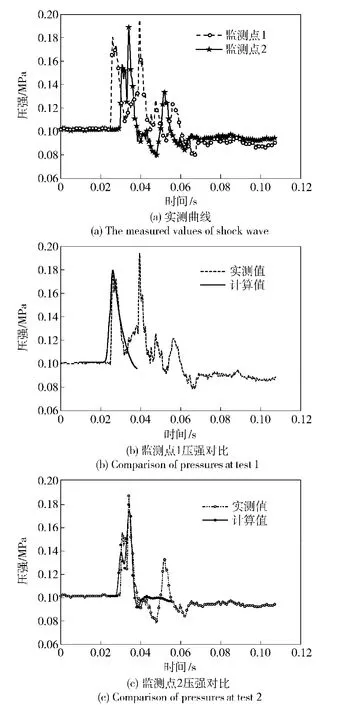
图5 监测点压强变化曲线Fig.5 Curves of pressures at monitoring points

图7所示为堵盖运动1.5 ms后发射箱内仿真结果。图7(a)所示为箱内对称面上静压云图,在堵盖前端面受燃气流的作用存在一个高压强集中区,出现原因在于燃气流对堵盖的冲击作用使堵盖端面上存在速度滞止区,在相应区域压强值较高。同时在发射箱后易碎盖端面的中心区域也存在高压区域。图7(b)所示为燃气流温度云图,燃气流沿着喷管壁向外流动,主流并未作用到易碎盖端面中心上。图7(c)所示为后易碎盖端面压强分布,后易碎盖端面的压强主要集中在堵盖的投影区域范围内,达到2.7×105Pa,易碎盖上整体平均压强略有升高,最低值达到1.42×105Pa.图7(d)为易碎盖端面上温度分布云图,温度分布由中心向外逐渐减弱,但总体温升较低,证明燃气流主流暂未接触易碎盖,同时在易碎盖上出现一个高温的环形区域,温度达到400 K.

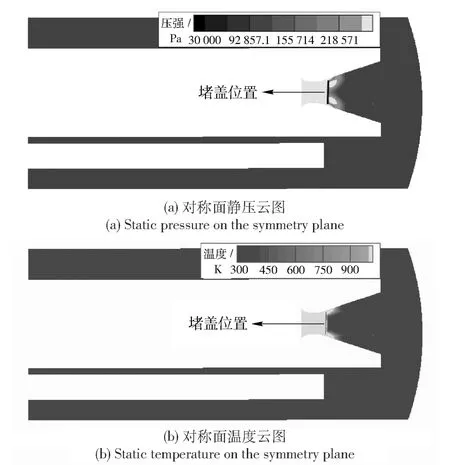
图6 堵盖运动0.5 ms后喷管内燃气流云图Fig.6 Contours of jet flow after 0.5 ms

由图7分析结果可知:受堵盖影响,燃气流与初始冲击波作用位置不同,并且冲击波形成于燃气流前端,其形状与燃气流边界形状也有所不同。

图8所示为堵盖运动3 ms飞出喷管后仿真结果。图8(a)所示在堵盖前端面上压强较低,证明燃气流在喷管内充分膨胀。而在堵盖后部静压值较高,接近3×105Pa.图8(b)所示燃气流温度云图,此刻燃气流已经冲击到发射箱易碎盖上并反向向前流动,发射箱后部空间被燃气流所填充,温度趋于一致接近1 900 K,而在堵盖前后端面被燃气流包围的包覆层,温度略高,在2 600 K左右。图8(c)所示为发射箱后易碎盖端面上压强云图,如图8(c)所示,在燃气流作下,在堵盖投影的中心区域内压强最大,达到4.67×105Pa,并向外逐渐减小。图8(d)所示为发射箱后端面上温度云图,从图中可以看出易碎盖上大部分区域温度约为2 200 K,局部有小范围的高温区域,接近2 400 K.在易碎盖下半部分燃气流温度略低。造成这种现象的原因在于底部的导轨阻碍燃气流的扩散,在该部位燃气流产生壅塞现象。

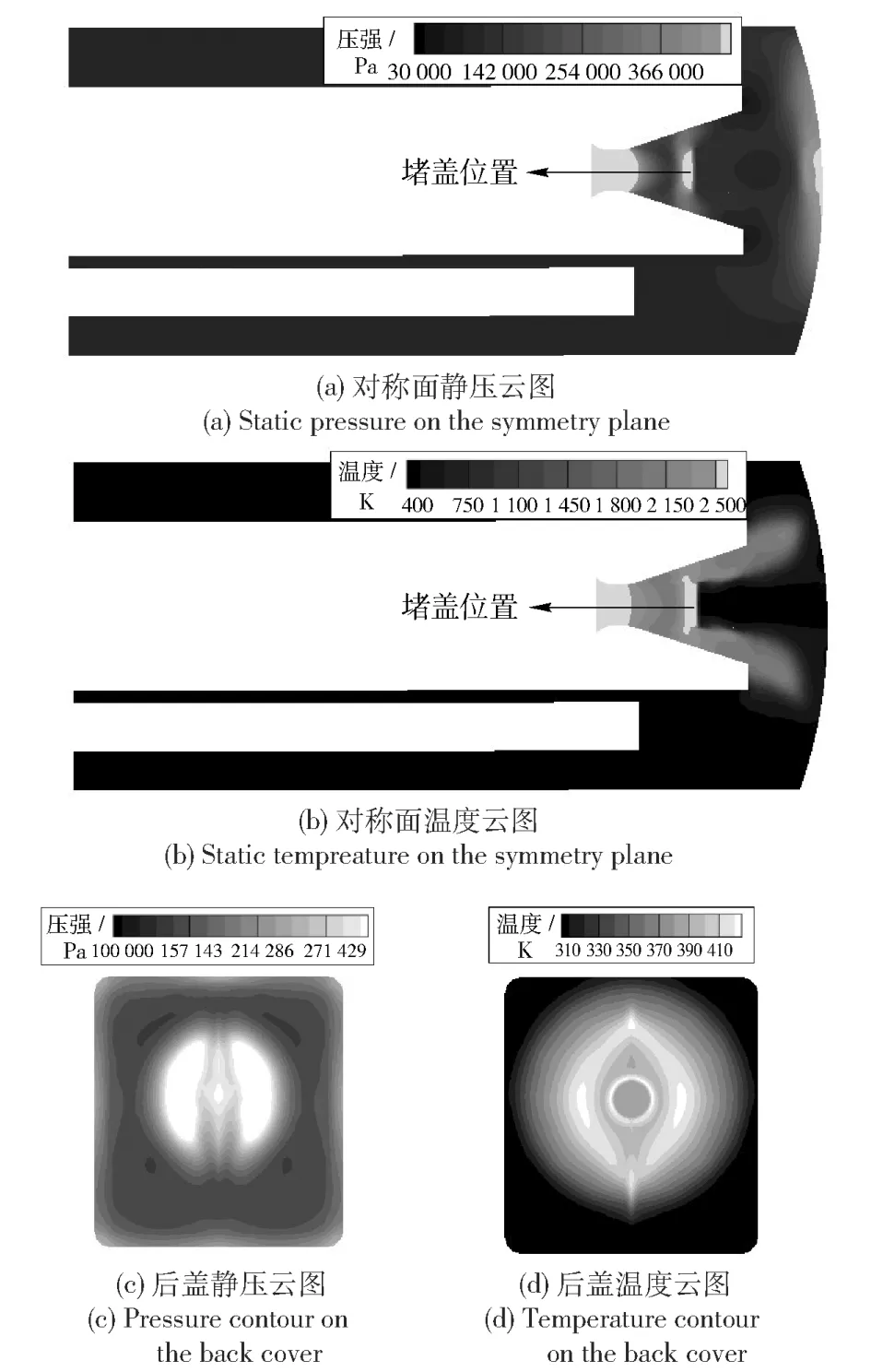
图7 1.5 ms流场仿真结果Fig.7 Contours of jet flows at 1.5 ms

3.2 仿真数据分析

为具体说明燃气流在堵盖运动过程中的作用效果,通过读取堵盖的速度值、堵盖两侧的压强值说明燃气流与堵盖的相互作用,同时读取易碎盖端面上压强和受力,得到相应参数变化曲线,将后易碎盖按照堵盖的几何投影划分为堵盖投影区域和其他区域两部分进行对比分析,具体结果如图9～图13所示。

图9所示为堵盖速度变化曲线,从图中可知堵盖运动3.6 ms后撞击后易碎盖,在前1.5 ms运动过程中,燃气流对堵盖的作用基本稳定,堵盖作匀加速运动,1.5 ms后堵盖运动速度基本趋于平衡。

图10所示为堵盖前后端面静压变化曲线,从图中可知堵盖前端面压强在堵盖初始运动时经过小范围的波动后逐渐降低并在末尾时刻降低到1×105Pa,后端面压强变化平缓,基本在2×105Pa附近波动,从初始环境压强逐渐升高并伴有小幅的波动发生,在堵盖运动2.2 ms时刻,前后端面压强相等,随后后端面压强高于前端面,堵盖受力反向作减速运动直至3.5 ms时刻撞击至后易碎盖。

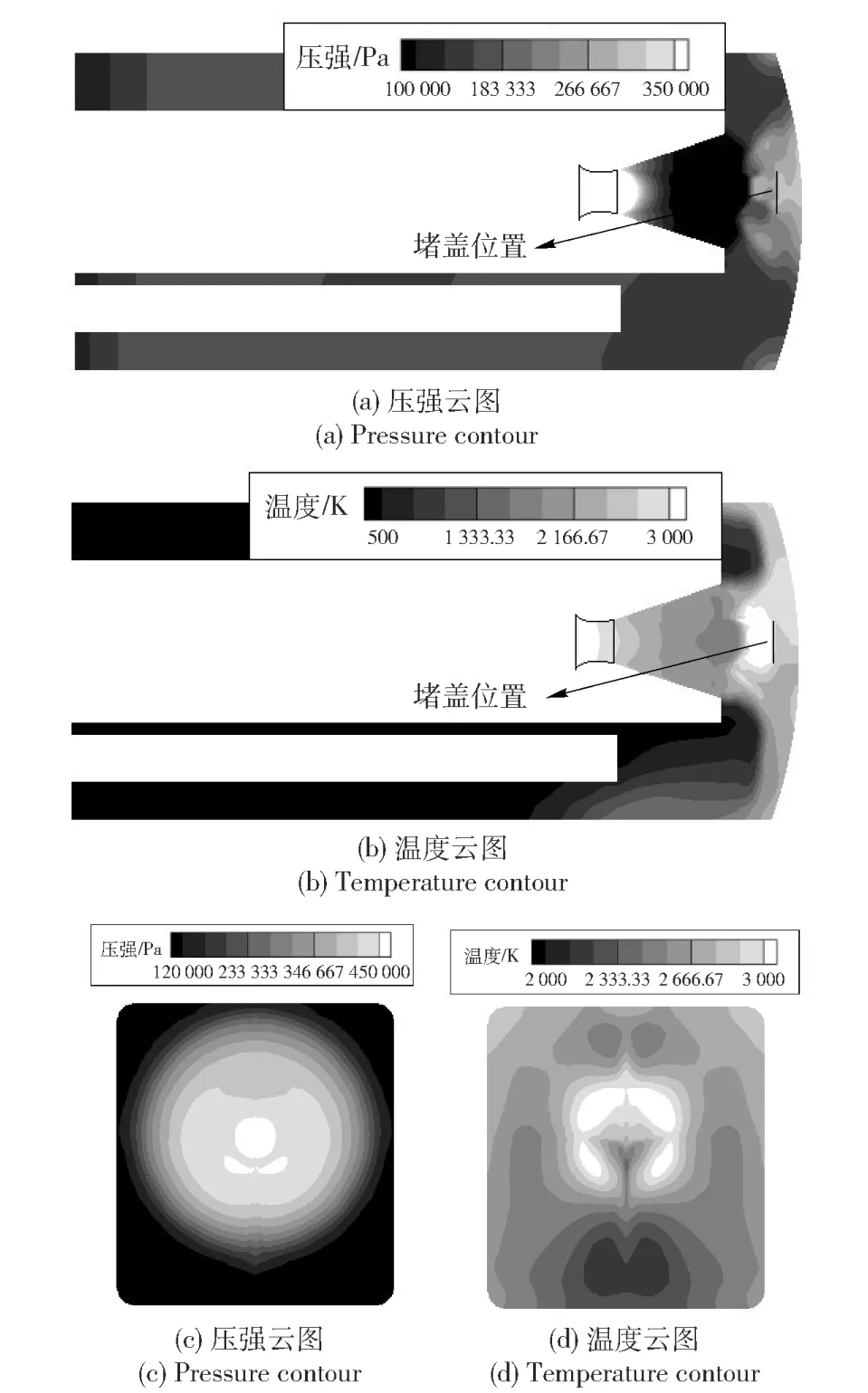
图8 3 ms流场仿真结果Fig.8 Contours of jet flows at 3 ms

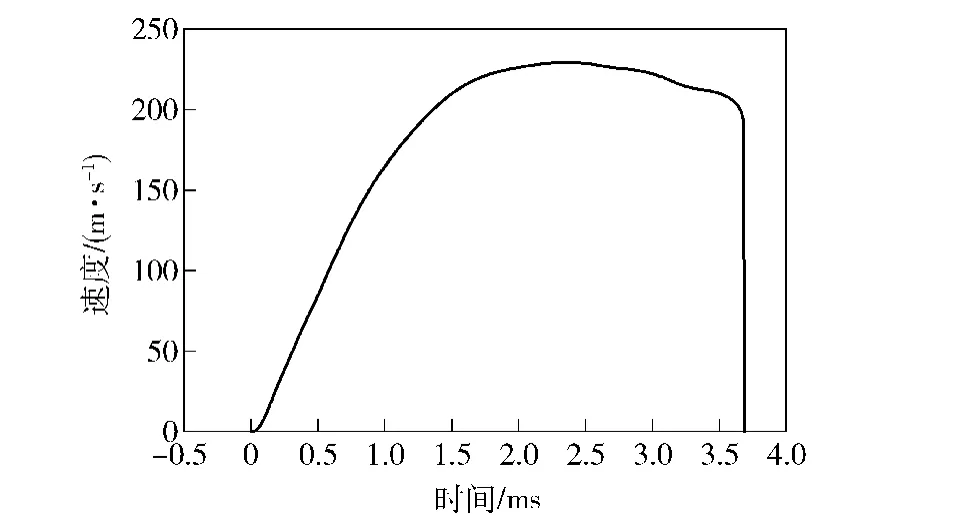
图9 堵盖速度曲线Fig.9 Velocity curve of nozzle closure

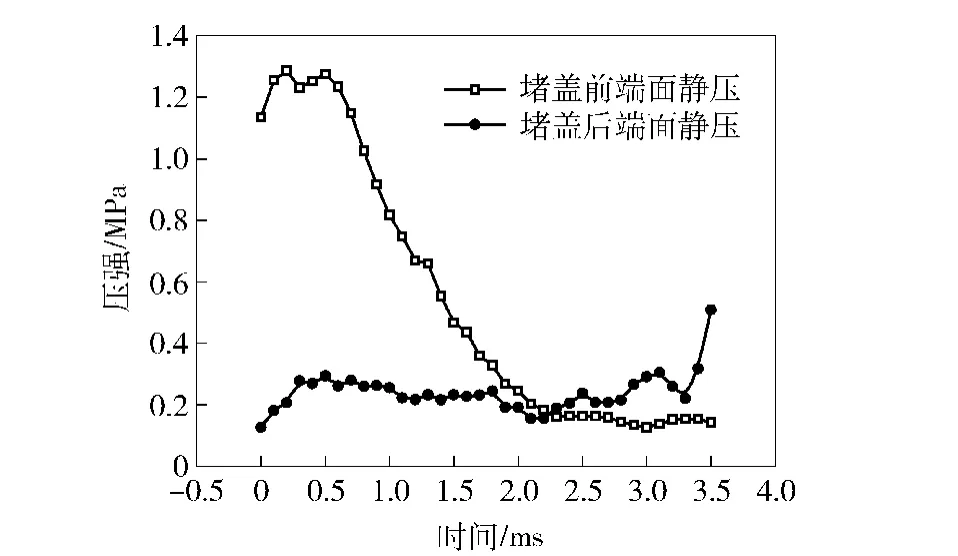
图10 堵盖前后端面压强曲线Fig.10 Pressures on the surface of nozzle closure

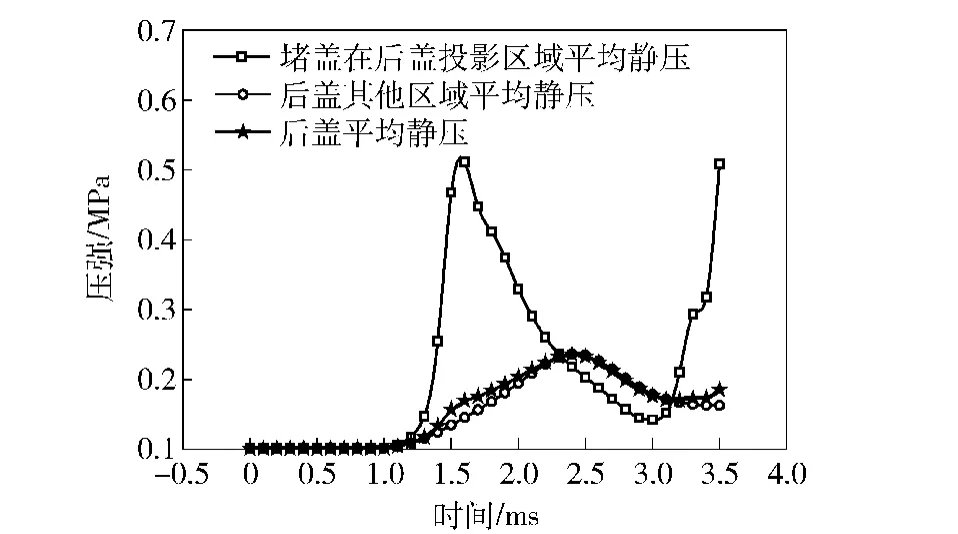
图11 后易碎盖端面平均压强曲线Fig.11 Average pressures on the surface of back cover

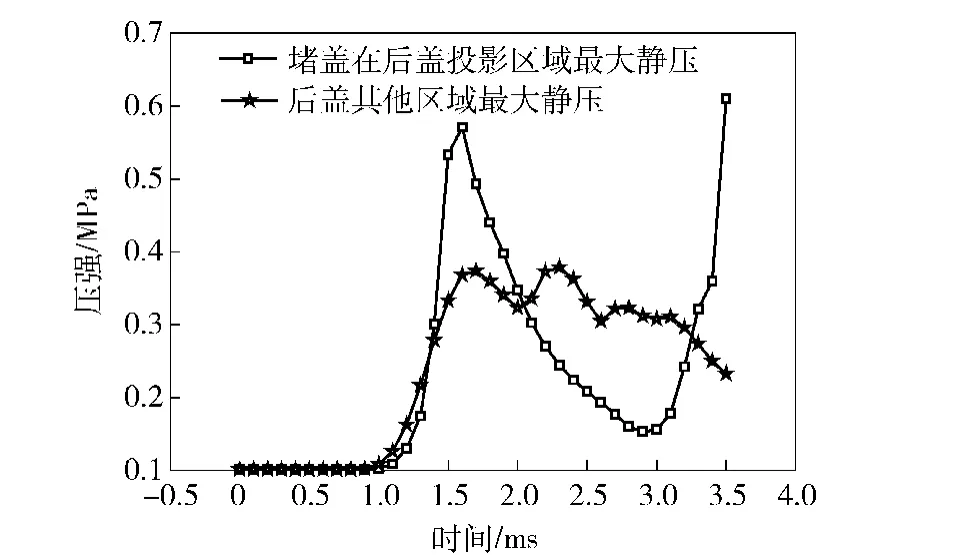
图12 后易碎盖端面最大压强曲线Fig.12 Maximum pressures on the surface of back cover

为说明后盖上压强分布规律,图11和图12所示压强曲线中分别给出了后盖上在堵盖投影区域和除投影区域外的平均静压和最大静压变化曲线以及整个后盖平均压强曲线,从图11所示的压强变化曲线中看出,在堵盖投影区域出现峰值的1.5 ms时刻,后盖上其他区域并未有明显的波动,而整个后盖端面上峰值出现时刻在2.5 ms,落后于该点,由此说明在投影区域所出现的峰值由冲击波形成,后盖整体的压强峰值由燃气流造成。同时可以看出在后易碎盖端面上堵盖投影区域压强较大,首先受到破坏。

从图12的最大压强变化曲线上分析,在后盖端面上除投影区域外压强最大值点出现两次峰值,并且第1次峰值出现时刻与堵盖投影区域峰值出现时间一致,说明两个表面峰值点由同一因素作用所致。而第2次峰值点的出现时刻堵盖投影区域并未出现明显波动,因此可以断定为燃气流作用,更有力地证明了冲击波与燃气流作用的时间先后性以及作用位置的差别。并且从冲击波峰值曲线上可以判断初始冲击波的作用范围和强度。

图13为堵盖和易碎盖上的受力曲线,对比压强变化曲线可知,二者的受力变化曲线与压强变化基本一致,从易碎盖受力曲线上可以判断在1.5 ms冲击波达到峰值时刻由于其在易碎盖上作用区域集中并且相对面积较小,因此对于整个箱盖的受力影响不明显。图中箱盖受力曲线可以为易碎盖的设计强度标准提供参考值。

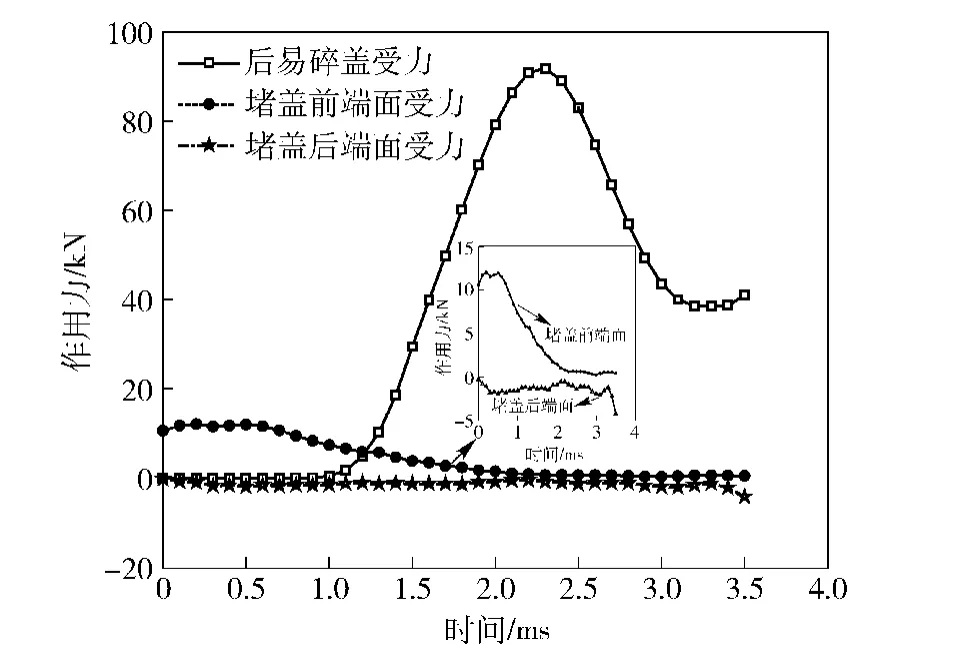
图13 堵盖和易碎盖上作用力曲线Fig.13 Forces on nozzle closure and back cover

4 综合实验验证

实验针对某型导弹点火过程利用高速摄影捕捉到发射箱后易碎盖的破碎过程,由于发射箱采用易碎盖设计,并且在导弹点火后易碎盖所处环境恶劣,无法直接在易碎盖上布置传感器,因此将监测点3放置于箱壁内壁面距离后易碎盖端面顶点0.55 m位置,如图1所示。实验中后易碎盖的设计开盖压力为0.06 MPa.由于在仿真过程中假设发射箱易碎盖达到开启压力后仍然封闭,而在实验过程中,后易碎盖被燃气流击碎。而在易碎盖破碎前,燃气流流动已经转向,会在监测点处出现第1个冲击波峰值,该峰值大小的仿真与实验值具有一定的可比性,因此只针对燃气流流经监测点的压力峰值对比,仿真实验数据峰值点绝对静压值为150 471.14 Pa,换算为表压值为0.049 MPa,实验过程中实测表压值0.055 MPa,仿真计算误差为3.14%,因此可以判断仿真结果存在较高的可信度。仿真数据曲线如图14所示。另外从图15的高速摄影图像中可以清晰看到在发射箱后易碎盖上首先是在箱盖中心出现与堵盖形状相同的圆形变形区域并破裂,随后从箱盖与箱体的结合部位有燃气溢出,因此实验过程验证了仿真结果的正确性。

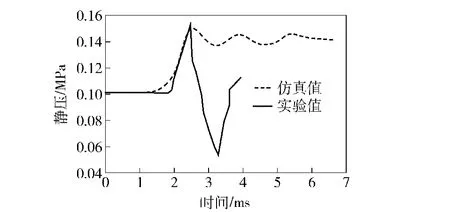
图14 监测点压力变化曲线Fig.14 Curves of static pressure at the monitoring point

图15 高速摄影实验结果Fig.15 High-speed photograph of experiment

5 结论

本文通过仿真与实验相结合的方法,分析了在尾喷管堵盖影响下的发射箱内燃气流场的作用以及初始冲击波的形成特点,获得了以下具体结论:

1)在有堵盖的燃气射流中,燃气流通过堵盖与喷管的缝隙流出并向喷管四周扩散,同时与堵盖后方滞止空气接触并形成初始冲击波阵面向外传播。

2)对于发射箱盖的作用冲击波先于燃气射流并且主要集中在堵盖的投影区域上,燃气流的冲击作用在易碎盖上首先形成围绕中心的环形区域,随后向四周扩散。

3)发射箱后盖同时受到冲击波和燃气射流的作用,冲击波的强度较大,作用区域集中,燃气流的冲击强度平均值略小,作用在整个后盖上,是发射箱后盖开启或破碎的主要因素。

4)堵盖在后盖的投影区域为整个箱盖上受力最严重的区域,首先被破坏,因此对于设计后易碎盖的破裂强度时应在此位置进行加强处理以避免在该区域首先被破坏的状态下达不到整体开盖压力。

References)

[1] 柯朗R,弗里德里克斯K O.超声速流与冲击波[M].李维新,徐华生,管楚洤,译.北京:科学出版社,1986.

Courant R,Friedrichs K O.Supersonic flow and shock waves[M]. LI Wei-xin,XU Hua-sheng,GUAN Chu-quan,translated.Beijing:Science Press,1986.(in Chinese)

[2] 苗佩云,袁曾凤.同心发射筒燃气开盖技术[J].北京理工大学学报,2004,24(4):283-285.

MIAO Pei-yun,YUAN Zeng-feng.Techniques for the automatic cover opening in concentric canister launcher[J].Transactions of Beijing Institute of Technology,2004,24(4):283-285.(in Chinese)

[3] JI H拉夫洛夫.固体火箭发动机结构[M].关正西,译.北京:中国宇航出版社,2006.

JI H Lavrov.Structure of solid rocket engine[M].Guan Zhengxi,translated.Beijing:China Astronautic Publishing House, 2006.(in Chinese)

[4] Arnab C,Abdellah H.Numerical simulation of transient supersonic nozzle flows[C]∥50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Nashville,TN:AIAA,2012.

[5] Steven S,Jacob D,James V.Experimental performance analysis of a toroidal aerospike nozzle integrated with a N2O/HTPB hybrid rocket motor[C]∥46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Nashville,TN:AIAA,2010.

[6] Binu P,Manhar D.Surface pressure fluctuations due to an impinging supersonic under expanded jet[C]∥48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Nashville,TN:AIAA.2010.

[7] 傅德彬,姜毅.某导弹易碎盖的开启过程[J].固体火箭技术, 2007,30(4):275-277.

FU De-bin,JIANG Yi.Opening process of friable lid of one missile[J].Journal of Solid Rocket Technology,2007,30(4):275-277.(in Chinese)

[8] 李学民.导弹发射箱(筒)内燃气流特性分析—热态试验研究[J].宇航学报,1997,18(4):67-74.

LI Xue-min.Characteristic analysis of missile combustion-gas in a launching-container(launching-tube)—hot experiment study[J]. Journal of Astronautics,1997,18(4):67-74.(in Chinese)

[9] 刘琦,傅德彬,姜毅.贮运发射箱内燃气射流的非定常冲击波流场数值模拟[J].弹箭与制导学报,2005,25(S4):382-384.

LIU Qi,FU De-bin,JIANG Yi.Unsteady simulation of shock wave in launcher[J].Journal of Projectiles,Rockets and Guidance,2005,25(S4):382-384.(in Chinese)

[10] 徐强,李开明,张福祥,等.封闭式导弹发射箱内燃气流特性实验研究[J].弹道学报,1995,7(2):52-56.

XU Qiang,LI Kai-ming,ZHANG Fu-xiang,et al.Experimental study of the internal exhaust flow field in closed rectangular missile launch tube[J].Journal of Ballistics,1995,7(2):52-56. (in Chinese)

[11] 徐强,李军.燃气射流起始冲击波形成机理的实验研究[J].推进技术,2000,21(3):16-18.

XU Qiang,LI Jun.Experimental study on mechanism of initial shock wave in jet flow[J].Journal of Propulsion Technology, 2000,21(3):16-18.(in Chinese)

[12] 赵承庆,姜毅.气体射流动力学[M].北京:北京理工大学出版社,1998.

ZHAO Cheng-qing,JIANG Yi.The kinetics of gas jet[M]. Beijing:Beijing Institute of Technology Press,1998.(in Chinese)

Research on Distribution of Flow Field in Launching Canister with the Effect of Nozzle Closure

YU Shao-zhen1,JIANG Yi1,ZHOU Xiao-fei1,NIU Yu-sen1,SUN Lu-lu2
(1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;
2.Naval Aeronautical Engineering Academy Qingdao Branch,Qingdao 266041,Shandong,China)

The overpressure of shock wave is widely used in opening the launching canister.In order to study the formation of shock wave and its effect on the fragile lid with a nozzle closure,a simulation model is established by using a numerical method,in which a dynamic mesh technique is used to update the meshes of flow field.The simulation results are verified with the experimental results.The formation process of jet flow is shown clearly and the changing curves of the overpressure on the back lid with time are obtained from the analysis results.The research results show that the overpressure of shock wave forms on the nozzle closure and then impact the fragile lid.The gas converges from the edge of nozzle closure to the center to form a mainstream.The effects of the mainstream and the shock wave on the back fragile lid are obviously different in impact time and position.The back fragile lid is brittlely deformed under the action of overpressure of shock wave.In the projection area of the nozzle closure,the instantaneous peak first reaches to the maximum value of 5×105Pa.

ordnance science and technology;nozzle closure;shock wave;fragile lid;numerical simulation

TJ760

A

1000-1093(2014)11-1805-08

10.3969/j.issn.1000-1093.2014.11.011

2013-12-13

于邵祯(1985—),男,博士研究生。E-mail:bitysz@bit.edu.cn;

姜毅(1965—),男,教授,博士生导师。E-mail:jy2818@163.com