基于降维可视化技术的结构可靠性灵敏度分析

李皓川,孙志礼,王海

(1.东北大学机械工程与自动化学院,辽宁沈阳 110819;2.沈阳金鑫宏美物资有限公司,辽宁沈阳 110001)

基于降维可视化技术的结构可靠性灵敏度分析

李皓川1,孙志礼1,王海2

(1.东北大学机械工程与自动化学院,辽宁沈阳 110819;2.沈阳金鑫宏美物资有限公司,辽宁沈阳 110001)

针对多维隐式结构可靠性问题,应用降维可视化技术进行可靠性灵敏度分析。基于iHLRF法求解设计点,根据模型计算精度确定有限差分步长。用一条直线将平面分为安全域和失效域两部分,通过计算直线初始位置附近数据点对应的响应量,来调整并确定直线的最终位置,根据直线上方数据点提供的信息计算可靠性灵敏度。提出的可靠性灵敏度分析方法的准确性不受维度以及非线性的影响,且效率较高。最后计算了两个结构系统的可靠度及各个变量的可靠性灵敏度,为结构设计提供了理论依据。算例表明了文中所给出的计算公式的正确性和有效性。

应用统计数学;结构可靠性;可靠性灵敏度;设计点;降维可视化技术;iHLRF法

0 引言

可靠性灵敏度分析为研究影响结构可靠性的主要因素提供了一种有效方法,其分析效果主要受可靠性分析方法的影响。对于复杂结构的可靠性问题,极限状态函数一般都没有解析表达式,即是隐式的。针对这一情况,经典的可靠性及可靠性灵敏度分析方法如一次可靠性方法(FORM)、二次可靠性方法(SORM)等解析法,由于其对高度非线性函数的近似效果不佳,因而精度不高[1-4]。取而代之的是改进的数字模拟方法,如重要抽样法(ISM)、子集模拟法、线抽样法和方向抽样法等,或是代理模型近似技术,如响应面法、神经网络技术、Kriging模型和支持向量机等[5-7]。然而这些方法应用在多维情况下都很困难,或是因为中间过程繁琐,或是因为需要计算大量样本的响应量,这被称为“维度灾难[8-12]”现象,从而降低了可靠性灵敏度分析的精度或效率。降维可视化技术[13](DRV)属于一种改进的数字模拟方法。通过提取样本的极特征信息并在平面内显示,将可靠性问题的研究从传统的标准正态空间转换到了平面内,并利用映射到平面内的失效类数据点的聚集特性估算可靠度,其分析效果不受可靠性问题的非线性和维度的影响。应用降维可视化技术分析可靠性问题的关键在于设计点的求解,这是一个约束优化问题。一个被广泛使用的方法即iHLRF[14]法,这是一种基于梯度的线搜索方法。当结构响应的梯度能够被准确计算时,iHLRF法是一种准确且高效的方法,反之将会导致迭代无法收敛。对于隐式函数响应的梯度,一个最直接的计算方法是有限差分法,但差分步长的选择常没有规律却显著影响梯度的精度。

本文首先简要介绍降维可视化技术的基本思想;然后应用iHLRF法求解设计点,根据模型的计算精度来确定有限差分的步长,保证了迭代的收敛性;进而提出通过计算少量样本点的响应量就可以确定失效类数据点的个数,并利用失效类数据点提供的信息进行结构可靠性灵敏度分析。文中给出了分析方法的原理与具体步骤,最后用两个多维可靠性问题验证了所提方法的准确性。

1 降维可视化技术

用样本的极特征作为平面直角坐标系的坐标,这样就可将标准正态空间中的样本点映射到平面内,若同时将数据结果的类标信息一并显示,即可靠性分析中的失效类和安全类,就实现了样本信息的降维可视化,就可在平面内用散点图来显示数据的分布情况。文献[13]已经讨论了在小概率情况下,从标准正态随机变量空间映射到平面内的失效类数据点具有显著的聚集特性,并且可由一条直线将平面内的两类数据点分开。例如下面的极限状态函数

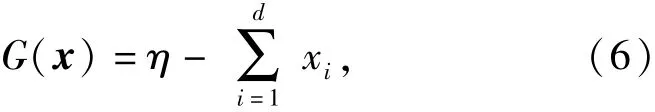
式中:各随机变量xi均服从参数值为1的指数分布; η为常数。应用Rosenblatt变换将极限状态函数转换到标准正态空间下如(7)式所示:

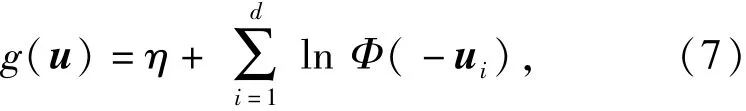
其设计点向量的方向为n=(1,1,…,1).令d= 30,η=46,产生50 000个样本点,将其映射到平面内,计算样本的类标信息如图1所示。可以看出失效类样本在极特征平面内有显著的聚集特性,且可由一条直线将两类数据点隔开,如图1中的实线。

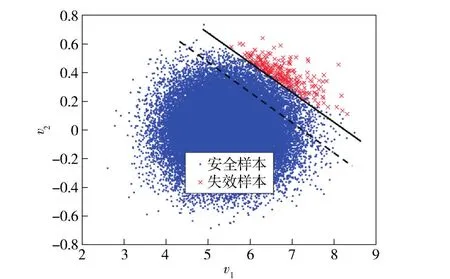
图1 样本信息的降维可视化Fig.1 Dimensionality reduction and visualization of samples'information

2 考虑计算精度的iHLRF法

式中:u=T(x)为原始随机变量与标准正态随机变量间的转换关系;∂G(x)/∂xi为极限状态函数相对于原始随机变量的偏导数。由于在工程问题中G(x)常由有限元方法计算,其相对于原始随机变量的偏导数的解析解很难得到,因此常采用有限差分方法计算,即

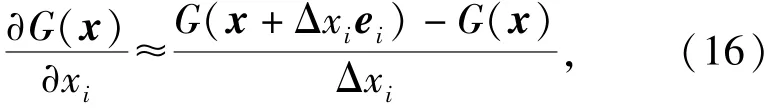
式中:Γxi为有限差分的步长;ei为xi轴上的单位向量。理论上差分步长越小,(16)式的截断误差就越小,但是应该根据模型的计算精度来选择步长大小。一般极限状态函数的响应包括两部分:一部分是确定性的,而另一部分是随机性的,这种随机性是由计算机的舍入误差和数值分析误差造成的,通常与模型的计算精度以及响应值呈一定的比例。如果步长Γxi太小,可能造成差分G(x+Γxiei)-G(x)的值比响应G(x)的随机部分还要小,这样计算的偏导数值误差将很大,甚至会造成迭代过程不收敛。因此差分步长应该足够大,使得极限状态函数响应值的随机部分可以被忽略。本文采用(17)式作为每一步的差分步长:

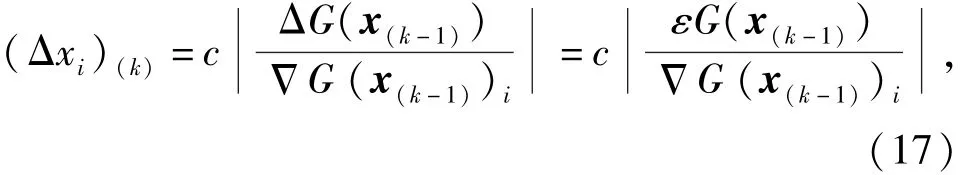
式中:c为放大倍数;ε为模型计算精度;εG(x(k-1))为极限状态函数的最大数值误差;ΓG(x(k-1))i为第k-1次迭代的梯度向量中的第i个元素。第一次迭代时,由于前一次的梯度向量未知,可以采用一个较大的差分步长。计算精度需根据极限状态函数的特性决定,如果G(x)是解析表达式,则ε一般应取10-8,如果G(x)是由数值计算确定的,如有限元分析,则ε应该根据数值分析的收敛标准确定,一般取10-5～10-4之间。

3 计算可靠性灵敏度

3.1 直线位置的确定方法

映射到平面内的失效类数据点均聚集在某一特定的位置,且落在一条直线上方。因此可将这条直线下方的安全类数据点截去,只需根据上方数据点提供的信息即可估算可靠度与可靠性灵敏度。但在调用极限状态函数计算之前,映射到极特征平面内的数据点没有类标信息,因此无法直观确定直线的位置。文献[13]提出根据经验确定直线位置,即根据失效类数据点常出现聚集的位置确定一条直线,留出较大的裕度,如图1中的虚线,计算直线上方所有数据点的类标信息,根据失效类数据点的个数估算可靠度。然而这种方法需要计算较多次极限状态函数的响应。为了尽量减少极限状态函数的调用次数,本文首先根据经验预判断直线的初始位置,然后根据其附近数据点的类标信息做出调整,达到最终位置,可以节省调用极限状态函数的次数,提高计算效率。下面介绍调整直线位置的具体步骤。

1)根据随机变量的维度在极特征平面内画出可靠性图的轮廓(使极特征的联合概率密度函数等于0)。

2)在标准正态空间中产生N个样本点,并将其映射到极特征平面内(此时极特征平面内的数据点是没有类标信息的,如图2中的白色数据点)。

3)预判断直线的初始位置。根据经验,中低维情况下直线在可靠性图的右上部分(可以将其设置为同时通过可靠性图最上端点与最右端点,如图2中的虚线),而高维情况下则在可靠性图的上方接近水平(可以将其设置为水平直线并在可靠性图上1/4处)。

4)计算初始直线和可靠性图轮廓的交点A、B附近数据点的类标信息。在A点附近,顺时针进行时,当计算得到连续两个失效类数据点即停止计算;逆时针进行时,当连续得到两个安全类数据点即停止计算。在B点附近,顺时针进行时,当计算得到连续两个安全类数据点即停止计算;逆时针进行时,当连续得到两个失效类数据点时即停止计算。

5)调整直线位置。使其同时通过临界处的两个失效类数据点,即确定了直线的位置。

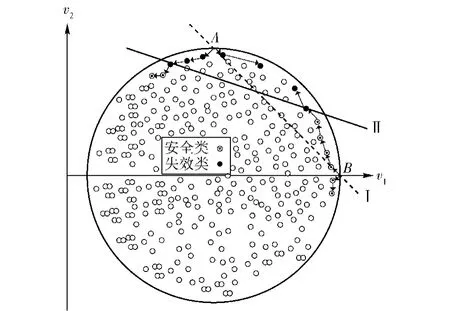
图2 直线位置调整示意图Fig.2 Schematic diagram of adjustment strategy of straight line

图2为调整直线位置的示意图,虚线为直线初始位置,实线为调整后的位置,箭头指示的是数据点的计算顺序以及停止时机。

这样只需要调用很少次极限状态函数就可以将安全类数据点和失效类数据点隔开。

3.2 计算可靠度及可靠性灵敏度

当确定直线的位置后,统计得到直线上方数据点个数Nup,则失效概率为式中:xh可通过标准正态空间中的失效样本点进行变换得到,而直线上方的数据点则储存标准正态空间中失效样本点的坐标信息。

4 实例分析

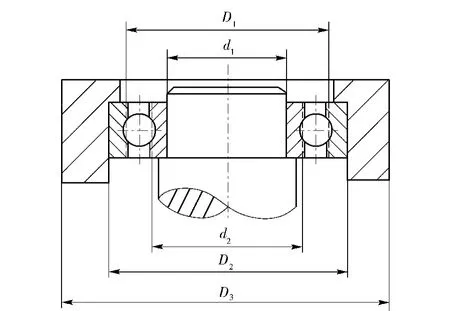
图3 轴承内外圈配合情况Fig.3 Fit situation of bearing's inner and outer rings

算例1为了防止传动轴发生抱死事故,轴承的工作游隙值应大于0 μm,即工作游隙的极限状态函数为G(x)=μw(x)-0,其中μw(·)为工作游隙函数,同时考虑配合、内圈转速、温升以及轴承材料等随机因素的影响。图3表示的是轴承内外圈的配合情况。

表1给出了影响滚动轴承游隙的随机变量及其分布参数。假设各随机变量均服从正态分布且相互独立。

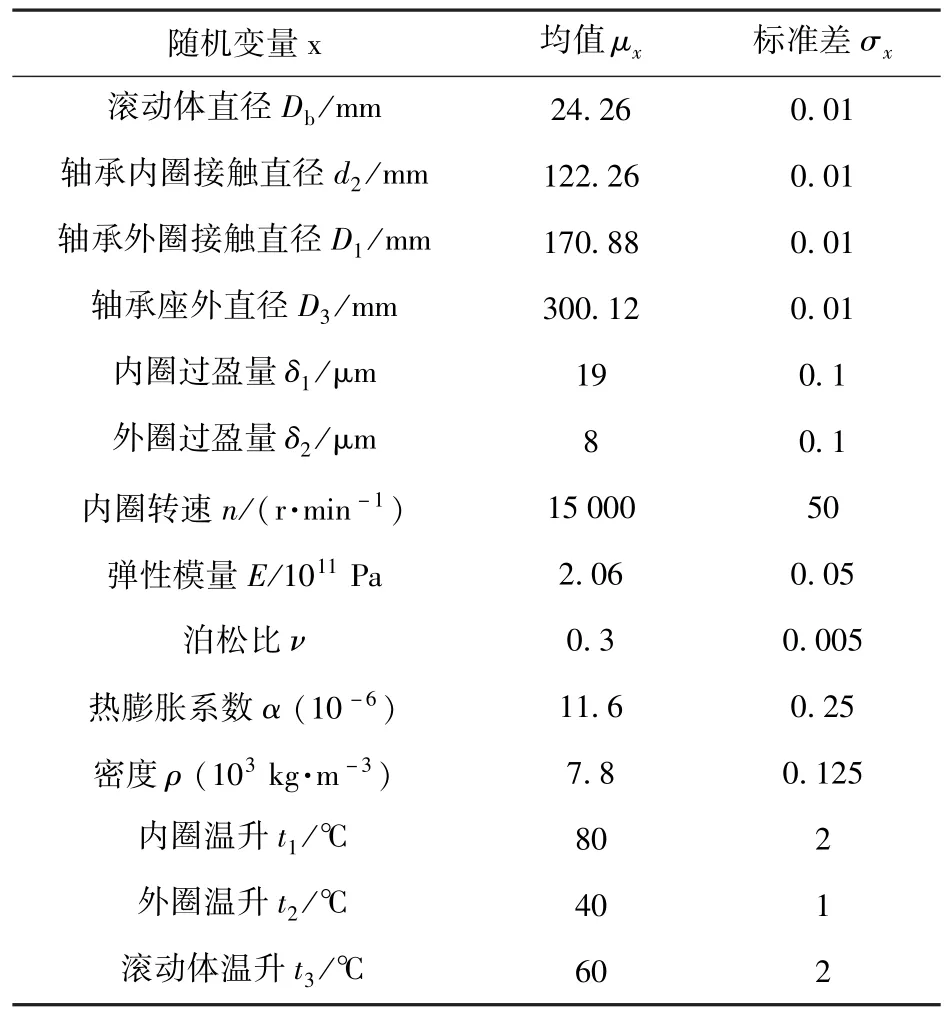
表1 随机变量分布参数列表Tab.1 Distribution parameters of random variables

此外,轴承内圈与轴配合直径d1为80 mm,轴承外圈与轴承座配合直径D2为200 mm.分别计算轴承内圈外径、外圈内径以及滚动体对工作游隙的影响,然后进行叠加,工作游隙的具体分析方法可参考文献[15]。

应用Rosenblatt变换将极限状态函数转换到标准正态随机变量空间,应用iHLRF法求解设计点,迭代停止的条件为‖u(k+1)-u(k)‖≤0.001.若每次的差分步长都设为定值,当迭代停止时,最终计算的设计点并不在极限状态面上,即不满足收敛条件|g(u*)/g(u0)|≤0.001,这是因为梯度计算出现较大误差,导致迭代步长非常小,使迭代无法继续进行。若采用(17)式的差分步长,放大倍数设为c= 5,模型计算精度设为ε=10-5,则能够保证迭代的收敛。最终计算的设计点u*为(2.182,1.092, -1.091,0,0.007,-0.008,0.013,-0.048, -0.003,0.163,0.032,0.31,-0.217,0.123).产生N=10 000个样本点并将其映射到平面内,调用22次极限状态函数得到调整后的直线位置如图4所示。截去下方数据点,统计直线上方共有Nup= 27个数据点,因此失效概率Pf=Nup/N=0.002 7.根据得到的设计点应用FORM、SORM以及ISM估算可靠度,结果如表2所示。

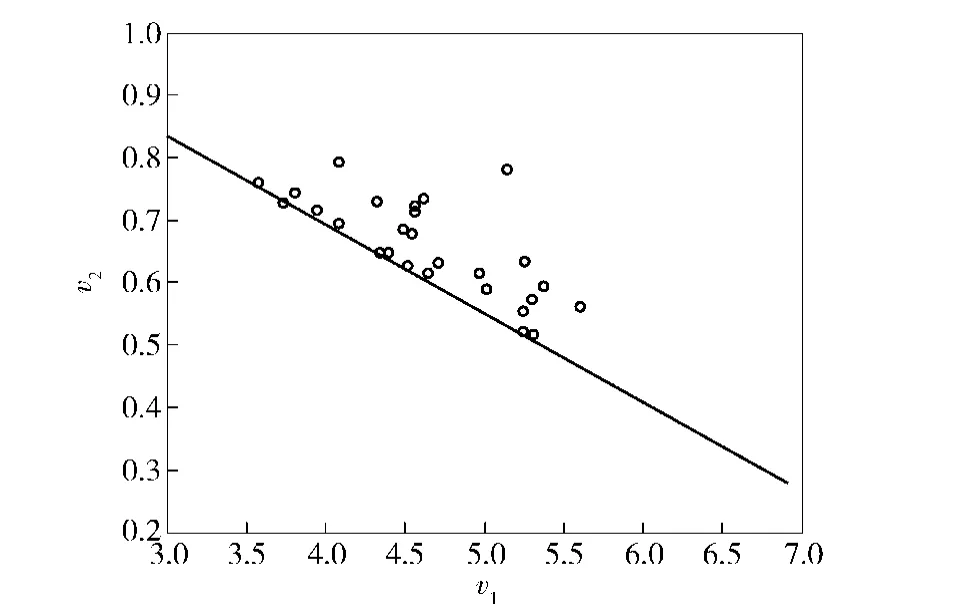
图4 滚动轴承工作游隙可靠性问题的截断直线Fig.4 Truncation line for reliability analysis of rolling bearing clearance

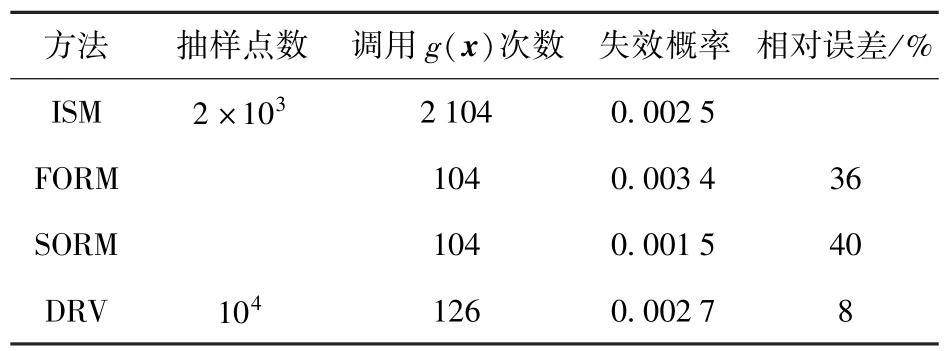
表2 算例1可靠度计算结果Tab.2 Calculated results of Example 1

虽然本问题中的随机变量均服从正态分布,但由于随机变量个数较多,且接触分析给极限状态函数带来了非线性,因此解析法对失效样本点的捕捉能力欠佳,出现了较大的误差。而本文方法只比解析法多调用较少次数的极限状态函数,却得到了与精确解相似的精度,这是由于其利用了失效样本点在标准正态空间中的分布规律,并直接从最可能失效区域进行搜索。将直线上方数据点对应的原始随机变量空间中的样本点坐标代入(24)式计算可靠性灵敏度,结果如表3、表4所示,其与通常的定性分析的结果吻合,可为轴承游隙的设计提供定量的理论依据。由于是利用失效样本点的坐标信息估计可靠性灵敏度,而通过可靠性分析的结果可知,截断直线上方的数据点提供的信息是准确的,因此利用其计算的可靠性灵敏度结果必然最接近精确解。

算例2一个7层的框架结构在顶部有均布的载荷40 kN/m,框架底部完全固定,如图5所示。

本问题共含有31个随机变量,即水平力(F1～F7),8种不同梁单元的实常数,即截面积(A1～A8)、抗弯惯性矩(I1～I8)以及截面高度(h1～h8)已在图5中表示。分布情况如表5所示,假设各随机变量相互独立。弹性模量E=5×1011Pa,泊松比ν=

表3 均值可靠性灵敏度计算结果Tab.3 Calculated results of reliability sensitivity for mean value

表4 标准差可靠性灵敏度计算结果Tab.4 Calculated results of reliability sensitivity for standard deviation

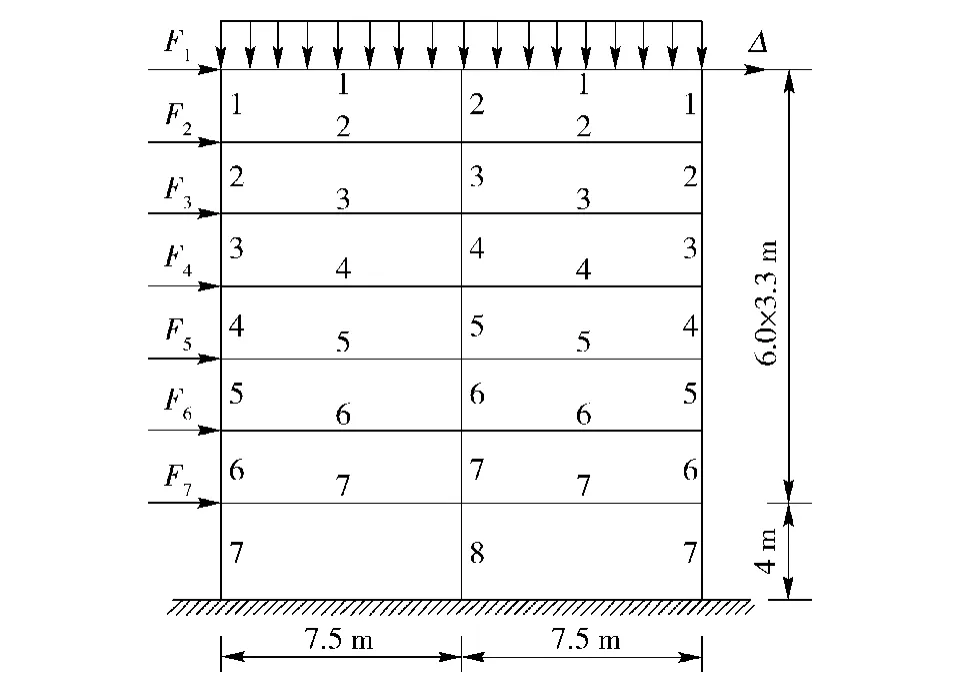
图5 7层平面框架Fig.5 Plane frame structure with seven layers

0.3,考虑钢筋混凝土的质量(密度取2.5 t/m3)。

若规定右上方的水平位移不能超过20 mm,则极限状态函数为G(x)=20-Δ(x).将随机变量转换为标准正态分布变量,将差分步长公式中的放大倍数设为c=5,模型计算精度设为ε=10-4,求得设计点u*为(0.000 4,-0.000 3,-0.000 7,-0.003 4, -0.009 1,-0.021 2,-0.038 4,0.000 4, -0.011 8,-0.060 8,-0.108 0,-0.166 0, -0.225 1,-0.531 9,-3.362 4,-0.457 6,0,0,0, 0,0,0,0,0,0.0332,0.0566,0.0691,0.0851,0.0992, 0.113 9,0.097 2)。产生N=50 000个样本点并将其映射到极特征平面内,调用35次极限状态函数得到调整后的直线位置如图6所示。

截去下方数据点,统计直线上方共有Nup=36个数据点,因此失效概率Pf=Nup/N=7.2×10-4.根据得到的设计点应用FORM、SORM以及ISM估计可靠度,结果如表6所示。

表5 随机变量分布参数列表Tab.5 Distribution parameters of random variables

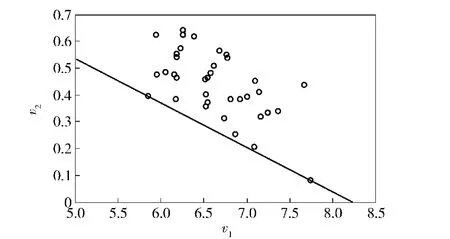
图6 框架结构可靠性问题的截断直线Fig.6 Truncated line for reliability analysis of frame structure

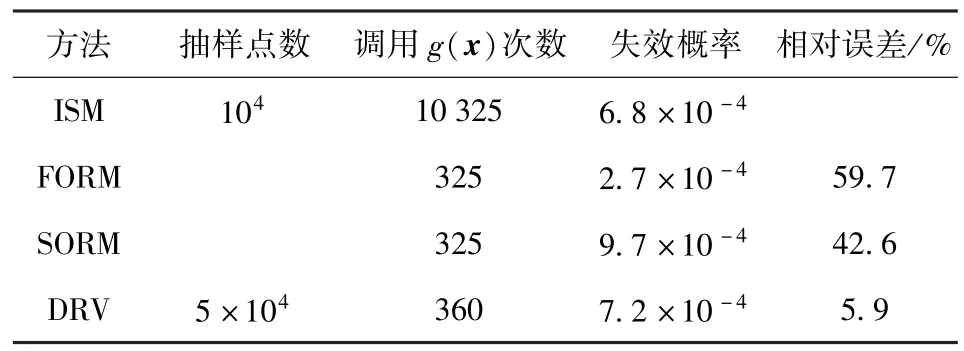
表6 算例2可靠度计算结果Tab.6 Calculated results of Example 2

本问题涉及的随机变量个数更多,并且由于水平力服从对数正态分布,因此在将其转换为标准正态变量时给极限状态函数带来了较强的非线性,应用降维可视化技术进行可靠性及可靠性灵敏度分析却不受之影响,且效率较高。考虑模型计算精度的差分步长的选取保障了iHLRF法的收敛,计算可靠性灵敏度的方法与算例1相同,由于变量较多,不再列出结果。

5 结论

1)本文提出的可靠性灵敏度分析方法是在平面内进行的,利用了映射到平面内的失效类数据点的高度聚集性,仅用一条直线上方的数据点提供的信息计算可靠性灵敏度,方法不受维度以及非线性的影响,且效率较高。

2)确定截断直线的方法仅需调用较少次数的极限状态函数,提高了降维可视化技术的效率。

3)根据模型计算精度确定的有限差分步长能够准确地求解极限状态函数响应的梯度,保证了应用iHLRF法求解设计点能够满足收敛条件。

4)方法规则,易于实现程序化。算例表明本文给出的基于降维可视化技术的可靠性灵敏度计算公式是有效和正确的。

References)

[1] Hurtado J E,Alvarez D A.A method for enhancing computational efficiency in Monte Carlo calculation of failure probabilities by exploiting FORM results[J].Computers&Structures,2013,117(2): 95-104.

[2] Zhao Y G,Ono T.A general procedure for first/second-order reliability method(FORM/SORM)[J].Structural Safety,1999, 21(2):95-112.

[3] Zhao Y G,Ono T.New approximations for SORM:Part 1[J]. Journal of Engineering Mechanics,1999,125(1):79-85.

[4] Zhao Y G,Ono T.New approximations for SORM:part II[J]. Journal of Engineering Mechanics,1999,125(1):86-93.

[5] Bourinet J M,Deheeger F,Lemaire M.Assessing small failure probabilities by combined subset simulation and support vector machines[J].Structural Safety,2011,33(6):343-353.

[6] Balesdent M,Morio J,Marzat J.Kriging-based adaptive importance sampling algorithms for rare event estimation[J].Structural Safety,2013,44(9):1-10.

[7] 刘瞻,张建国.基于优化Kriging模型和重要抽样法的结构可靠度混合算法[J].航空学报,2013,34(6):1347-1355.

LIU Zhan,ZHANG Jian-guo.Hybrid structure reliability method combining optimized Kriging model and importance sampling[J]. Acta Aeronautica et Astronautica Sinica,2013,34(6):1347-1355.(in Chinese)

[8] Bucher C.Asymptotic sampling for high-dimensional reliability analysis[J].Probabilistic Engineering Mechanics,2009,24(4): 504-510.

[9] Sichani M T,Nielsen S R K,Bucher C.Efficient estimation of first passage probability of high-dimensional nonlinear systems[J]. Probabilistic Engineering Mechanics,2011,26(4):539-549.

[10] Pettit C L,Wilson D K.Full-field sensitivity analysis through dimension reduction and probabilistic surrogate models[J].Probabilistic Engineering Mechanics,2010,25(4):380-392.

[11] Zhang X,Pandey M D.Structural reliability analysis based on the concepts of entropy,fractional moment and dimensional reduction method[J].Structural Safety,2013,43(3):28-40.

[12] Valdebenito M A,Pradlwarter H J,Schuëller G I.The role of the design point for calculating failure probabilities in view of dimensionality and structural nonlinearities[J].Structural Safety, 2010,32(2):101-111.

[13] Hurtado J E.Dimensionality reduction and visualization of structural reliability problems using polar features[J].Probabilistic Engineering Mechanics,2012,29:16-31.

[14] Liu P L,Der Kiureghian A.Optimization algorithms for structural reliability[J].Structural Safety,1991,9(3):161-177.

[15] 李皓川,孙志礼,闫明.高精密滚动轴承游隙的可靠性保障研究[J].东北大学学报:自然科学版,2014,35(10):1516-1520.

LI Hao-chuan,SUN Zhi-li,YAN Ming.Research on the reliability assurance of highly precise rolling bearing clearance[J]. Journal ofNortheasternUniversity:NatureScience,2014, 35(10):1516-1520.(in Chinese)

Analysis of Structural Reliability Sensitivity Based on Dimensionality Reduction and Visualization Technique

LI Hao-chuan1,SUN Zhi-li1,WANG Hai2
(1.School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,Liaoning,China; 2.Shenyang Jinxin Hongmei Materials Co.Ltd.,Shenyang 110001,Liaoning,China)

For the implicit reliability problem with multiple dimensions,the reliability sensitivity of structure is analyzed by applying the dimensionality reduction and visualization technique.The design point is found based on iHLRF method,and the step size of finite difference is determined according to the modeling computational precision.The plane is divided into two parts of safe domain and failure domain by a straight line,and the final position of the straight line is determined by calculating the responses corresponding to several data points nearby its initial position.The dimensionality and nonlinearity do not affect the accuracy of the proposed method,which also has relatively high efficiency.Finally,the reliabilities of two structural systems and the reliability sensitivities of various influencing factors are calculated, which provides a theoretical basis for designing the structural systems.The examples show that these theories and formulas are rational and efficient.

applied statistical mathematics;structural reliability;reliability sensitivity;design point; dimensionality reduction and visualization technique;iHLRF method

TB114.3

A

1000-1093(2014)11-1876-07

10.3969/j.issn.1000-1093.2014.11.020

2014-03-03

国家自然科学基金项目(51135003)

李皓川(1987—),男,博士研究生。E-mail:lhcneu@163.com;

孙志礼(1957—),男,教授,博士生导师。E-mail:zhlsun@mail.neu.edu.cn