基于多维特征参数的装备状态动态评估方法

王少华,张耀辉,韩小孩

(装甲兵工程学院技术保障工程系,北京 100072)

基于多维特征参数的装备状态动态评估方法

王少华,张耀辉,韩小孩

(装甲兵工程学院技术保障工程系,北京 100072)

针对目前状态评估方法多重视状态特征参数的静态观测值,对时序状态数据所蕴含的趋势信息关注较少的缺点,提出了静态评估与动态评估相结合的状态评估方法。针对多维状态特征条件下赋权难度大的问题,采用变尺度混沌算法进行客观赋权,建立了状态静态评估模型。在静态评估的基础上,提出运用劣化速度间的“距离”修正静态评估结果来进行动态评估。运用近邻样本密度加权的核模糊C均值聚类算法对劣化速度标准向量进行求解,提出了动态调整函数优化算法,建立了完整的装备状态动态评估模型。通过案例分析验证了该方法的有效性。

兵器科学与技术;多维特征参数;混沌优化算法;NSD-WKFCM聚类算法;动态评估

0 引言

状态评估是状态维修的关键技术之一,状态评估通过分析反映装备状态的各类特征参数的观测数据,运用评估方法获取装备所处的健康状态,为维修决策提供技术支持。不同的状态特征参数能够从不同的角度反映装备的状态,因此如何有效地融合高维的状态数据已经成为状态评估研究的重点[1]。目前,研究者主要采用距离函数法[2]、聚类评估法[3]、BP神经网络[4]、支持向量机分类法[5]、主成分分析法[6]、灰色评估法[7]、模糊综合评估法[8]以及这些方法的组合来融合状态特征数据,进行状态评估。

上述状态评估方法对特征参数的观测值进行融合,并未利用状态检测过程所包含的趋势信息,属于静态评估,相应的状态指标能够反映装备接近功能故障的程度,但无法描述装备状态接近功能故障的速度。状态劣化速度能够反映装备状态接近故障的速度,在状态评估中引入这一信息,将有助于提高状态评估的合理性。依据上述分析,本文以高维状态特征数据为输入,对如何在静态评估的基础上,利用状态劣化速度信息建立状态评估以及相应的维修决策模型进行研究。

典型的状态评估技术路径是通过对状态特征参数的线性、非线性融合来实现状态评估,即为静态评估。本文在静态评估的基础上,利用状态特征参数的劣化速度来构造函数,将该函数作为乘子来修正状态评估结果。理论上,对于静态评估结果相同的装备,状态劣化速度越快的,即作为乘子的函数应与状态劣化速度呈正比。由于状态劣化速度信息属于过程类信息,因此将上述乘子函数称为动态调整函数,图1所示为详细的建模流程。

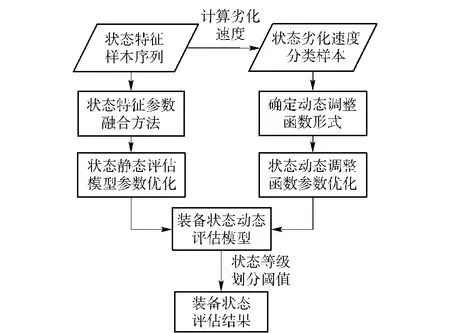
图1 装备状态动态评估建模流程Fig.1 Dynamic evaluation modeling process for equipment condition

如图1所示,装备状态评估建模过程主要包括静态评估模型的建立和动态调整函数的确定。其中,静态评估建模是直接对状态特征参数的观测值进行融合,首先选择状态特征参数的融合方法,文献[2-8]中列举了不同的数据融合方法,在确定融合方法的基础上,以观测样本为输入值,采用适用的算法对静态评估模型的参数进行优化。通过变尺度混沌优化为特征参数进行融合。动态调整函数的确定主要包括确定函数形式和参数优化。指数函数、双曲线函数等典型函数都能够作为动态调整函数,函数的选择主要取决于状态样本的复杂程度;对于动态调整函数的具体参数,主要是依据状态判别的结果来进行反馈调整。在确定静态评估模型和动态调整函数之后,即可将其相乘建立完整的状态评估模型,对状态指标进行阈值划分即可对状态等级进行评判,继而进行维修决策。

1 装备状态静态评估模型

在装备状态的定量评估方法中,加权求和模型具有广泛的应用基础,建模难度较低且易于理解,因此本文采用该方法构造状态指标,建立静态评估模型。建模的关键是特征权重的确定,装备状态特征参数具有维度高、含噪样本比例高的特点,导致主成分分析法等赋权评估方法应用效果不够理想,针对这一问题,本文提出采用变尺度混沌优化算法对特征参数权重进行优化,建立状态静态评估模型。

混沌优化方法作为典型的客观赋权法,能够通过映射在解空间内不重复地遍历寻优,具有极强的全局优化能力。大量实践表明,利用混沌变量寻优,效果明显优于模拟退火法和遗传算法等其他随机优化方法[9],文献[10-11]分别对混沌算法在连续对象优化中的应用进行了研究,但由于权重优化问题受归一化条件的约束,经典混沌优化算法的全局寻优能力受到了一定的影响,因此本文构造了尺度控制算子,对特征参数的权重进行变尺度混沌优化。

1.1 状态静态评估中的权值优化问题分析

基于加权求和法的静态评估模型的表达式为

依据状态维修决策过程,装备的状态可以分为“良好”、“劣化”和“危险”,其中“危险”指装备发生功能故障的风险超过可接受标准时的状态。装备达到“危险”状态时应及时进行状态维修,预防功能故障的发生。基于等级分类的状态评估的目的是最显著地区分处于已知状态的“良好”、“劣化”以及“危险”样本,因此最佳的特征参数权重应使不同状态等级的样本评估值之间的差异最大化,且使同类样本的评估值之间的离散度最小化,以达到提高状态辨识度的目的,据此提出权重优化目标函数F为

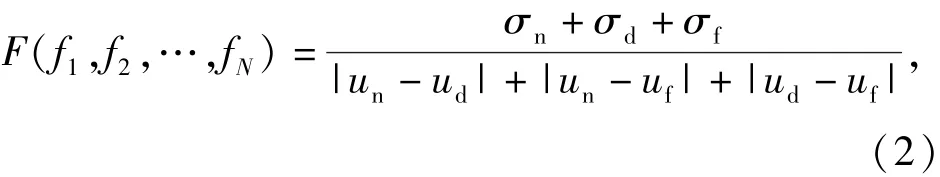
式中:f1,f2,…,fN为各特征参数的权重;σn、σd和σf为“良好”、“劣化”和“危险”类样本的状态评估值的标准差;un、ud和uf为“良好”、“劣化”和“危险”类样本的静态评估均值。F值越小,表明静态评估模型就越能灵敏地反映装备状态的变化,因此确定特征参数权重优化的目标函数为

1.2 状态特征参数权重的变尺度混沌优化

混沌是非线性系统所独有且广泛存在的一种非周期运动形式,混沌运动具有“遍历性”、“规律性”、“随机性”等特点,能够将系统运动吸引并束缚在特定的范围内,并不重复地遍历所有状态,因此混沌优化具有全局寻优的能力。

Logistic模型是最典型的混沌运动模型[11],其方程为

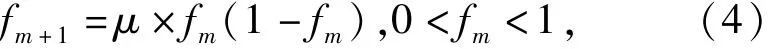
式中:μ为控制参数,取值0～4,当μ=4时,系统处于完全混沌状态。令Logistic模型随机赋初始值,可以得到在(0,1)上遍历的点列,因此采用Logistic模型生成混沌序列,将权重优化问题转化为在对应解空间中的混沌寻优问题,对权重进行优化。

假设有N个状态特征参数,则利用(4)式建立N个Logistic映射,表示为

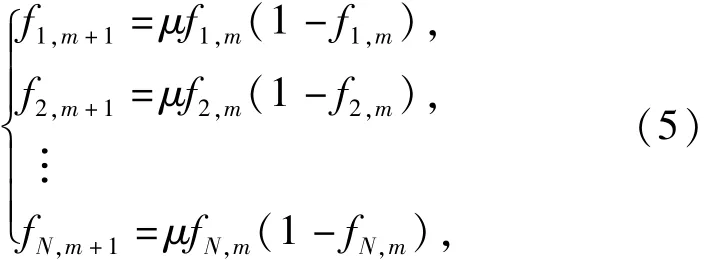
式中:fi,m(i=1,2,…,N)为第i个特征参数的权重寻优变量,令μ=4,即fi,m能够在(0,1)范围内遍历。由于混沌运动具有遍历性,只要有足够的迭代次数,最后都能够收敛到全局最优解。但由于受权重归一化的约束,该算法的遍历效率将受到极大影响。因此为了提高寻优效率,本文在混沌优化过程中引入外循环和内循环来进行变尺度优化,通过外循环缩小混沌遍历区间,通过内循环对迭代成功次数进行计数,以达到快速优化的目的。

基于变尺度混沌优化算法的特征参数权重优化步骤如下:

1)初始化:设置外循环次数阈值为K,内循环次数阈值为M,内循环迭代次数阈值为P,置外循环计数变量k=1,内循环计数变量m=1,内循环次优值计数变量times=0;置J的初值为一绝对大值,令变量的变尺度遍历区间[ai,bi]的初值为ai=0,bi= 1.

2)对(5)式中的混沌变量fi,m(i=1,2,…,N)在(0,1)内随机赋初始值。

3)将fi,m(i=1,2,…,N)映射到对应的混沌遍历区间内:f′i,m=ai+fi,m(bi-ai).

在变尺度过程中a′i和b′i可能出现负值,导致变量越界,为了使遍历范围保持在[0,1]内且保持缩小的趋势,对变尺度区间进行约束:若a′i＜ai,则令a′i=ai;若b′i＞bi,则令b′i=bi.

8)k=k+1,若k＜P,则令ai=a′i,bi=b′i,转向步骤3,否则转向步骤9.

2 装备状态动态评估模型

图2为两条状态劣化曲线,分别表示两台同型号装备静态评估指标的连续观测过程,曲线在P点相交,即在该点两台装备获得了相同的静态评估值,但实际上两台装备的剩余寿命或者功能故障风险是不同的,曲线斜率较大的,即劣化速度越快的其故障风险相对越高。因此利用劣化速度与风险的正相关关系修正静态评估模型是合理的。由图2可知,尽管每台装备都有唯一的劣化曲线,但也存在共有的特征,即装备特征参数的劣化速度在良好区和危险区具有聚类特性,在良好区通常“慢”,在危险区通常“快”,在劣化区则呈逐渐递增的趋势,即由“慢”逐渐向“快”转变。本文即利用这种关联关系,通过建立“慢”和“快”的标准向量,利用劣化速度与这两个向量的“距离”来表示装备接近功能故障的速度。

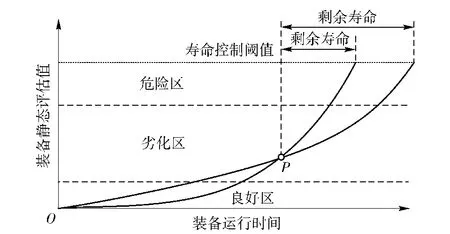
图2 装备状态劣化曲线Fig.2 Condition deterioration curves of equipment

2.1 动态调整函数的构造

构造动态调整函数的目的,是利用劣化速度来表示装备接近功能故障的速度,通过修正静态评估值来更加准确地表示实际的故障风险。本文利用劣化速度与标准向量间的距离构造动态调整函数,并将其与静态评估值相乘,得到完整的动态评估模型。本文采用一次倒数函数来构造动态调整函数:

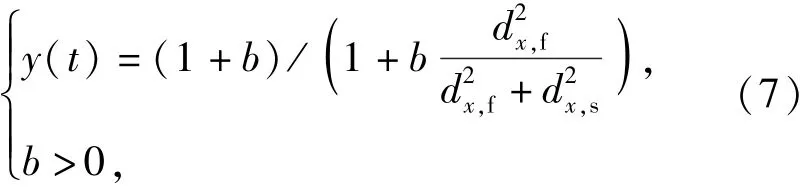
式中:y(t)为动态调整函数;b为控制参数;dx,s和dx,f分别表示待评估样本到vs和vf的欧氏距离, dx,s=‖x-vs‖,dx,f=‖x-vf‖,vs和vf分别为劣化速度“慢”和“快”的标准向量。则随着劣化速度从“慢”向“快”发展,y(t)的取值从1逐渐增加至1+b,使静态评估值的放大倍数与劣化速度呈正相关关系。

将静态评估模型与动态调整函数相乘,得到动态评估模型:

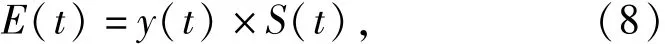
式中:E(t)为t时刻的动态评估值;y(t)为t时刻的动态调整函数值;S(t)为t时刻的静态评估值。动态调整函数的参数主要包括:劣化速度“慢”和“快”的标准向量和控制参数b.本文采用基于近邻样本密度加权的核模糊C均值聚类算法[12-13]求解劣化速度“慢”和“快”的标准向量,控制参数b通常根据实验情况进行优化确定。

2.2 劣化速度标准向量的求解算法

由于装备状态劣化过程具有随机性,在整个寿命过程中无法依据役龄直接将劣化速度划分为“快”或“慢”,即劣化速度存在模糊性,因此采用模糊聚类理论对vs和vf进行聚类分析。由于特征参数劣化速度数据具有高维、含噪的特点,常用的模糊聚类算法无法有效地处理此类数据,这里选择采用NSD-WKFCM(近邻样本密度-加权核模糊C均值)聚类算法对劣化速度进行聚类分析,该算法采用核方法将样本从采样空间映射到高维特征空间,在不增加系统VC维的条件下提高了处理线性不可分问题的能力,同时依据近邻样本密度进行加权,有效地降低了噪声数据的影响。

2.2.1 近邻样本密度加权算法

近邻样本密度加权算法的依据是:在聚类划分中,聚类样本应围绕聚类中心呈团状分布,即越靠近聚类中心的样本,其周围分布的样本越多,即在该样本点处的近邻样本密度越大,该样本点对于聚类的影响越大。因此依据近邻样本密度函数确定加权系数,可以有效降低远离聚类中心的噪声样本对聚类的影响。

采用高斯函数来定义点密度函数:

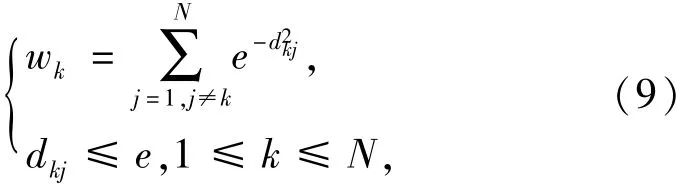
式中:dkj表示两个样本xk和xj的欧氏距离,dkj=‖xk-xj‖;N为样本容量;e为近邻范围域的阈值,有min(dkj)＜e＜max(dkj),样本xk附近的点越多,则wk的值就越大,该样本对聚类的作用越大,e的取值通常依据实验确定。

对wk进行归一化:

2.2.2 NSD-WKFCM聚类算法的迭代求解

假设φ是一个非线性映射函数,φ∶p∈OS→φ(p)∈HS,其中p是采样空间OS中的变量, φ(p)表示映射后的高维特征空间HS中的变量。NSD-WKFCM聚类算法的目标函数为

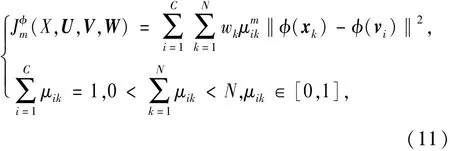
式中:X、U、V、W分别为样本、模糊隶属矩阵、模糊聚类中心、权重向量;C为聚类数;μik表示第k个样本对第i个聚类的隶属度;xk为P维样本向量;vi表示第i类的聚类中心;‖·‖表示基于核的距离度量,本文采用高斯核函数,则有

为了令Jφm(X,U,V,W)取最小值,从而求得最佳的聚类中心VC×P={vi}和模糊隶属矩阵UC×N= {μik},利用(11)式中的归一化约束条件构造拉格朗日函数:

利用(14)式和(15)式对模糊隶属矩阵UC×N和聚类中心VC×P进行迭代求解,具体步骤为:

1)给定样本集X,对样本进行归一化处理。设置聚类数C、平滑参数m、高斯核函数的尺度参数σ、邻近范围域阈值e,设置目标函数迭代截止误差ε和最大迭代次数T.

2)初始化聚类中心{vi}=VC×P.

3)计算样本间的核距离,利用(9)式和(10)式计算各样本的归一化权重ωk(1≤k≤N).

4)根据(14)式,用当前的聚类中心计算得到模糊隶属矩阵UC×N,构造迭代变量Vo、Uo和Vn、 Un,将当前VC×P和UC×N赋予Vo和Uo.

5)由(15)式构造迭代(16)式,计算聚类中心Vn={vi,n}:

7)若|Vn-Vo‖＜ε或迭代次数达到T,则终止迭代,输出聚类中心V和隶属度矩阵U;否则令Vo=Vn,Uo=Un,转到步骤5继续迭代。

这里构造初始聚类中心VC×P={vs;vf},其中vs和vf分别表示“慢”和“快”这两类速度向量的聚类中心,通过上述迭代求解过程可得到模糊聚类中心V.

2.3 基于定量动态评估的状态等级分类

装备状态的动态评估定量地描述装备实时故障风险,但为了降低维修决策层的工作难度,仍然需要对状态评估值域进行划分,输出定性评估结论,为实施及时有效的维修提供直观的信息。采用模糊评判法建立状态评判模型,评语集为{“良好”,“劣化”,“危险”}。

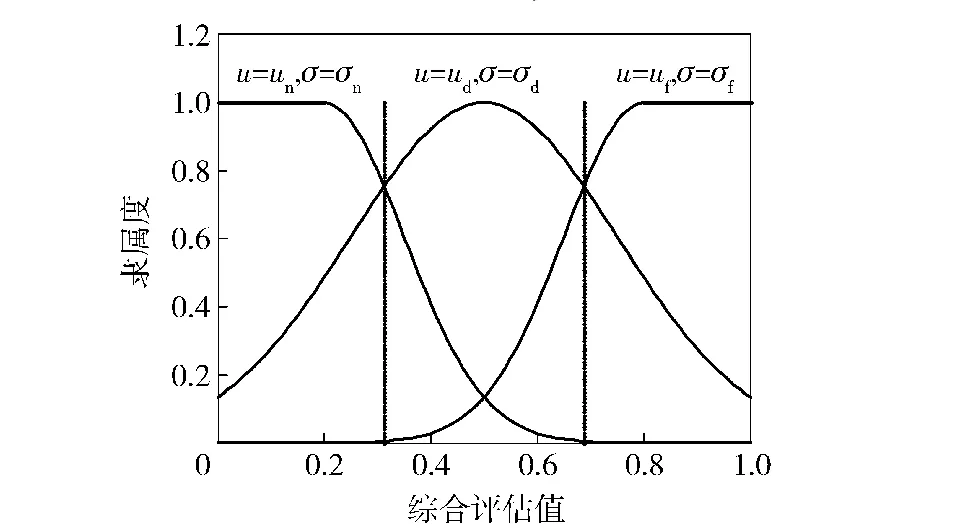
图3 各状态等级的模糊隶属函数Fig.3 Fuzzy membership function of condition grade

分别以un、ud、uf为中心,以σn、σd、σf为标准差构造高斯和单侧高斯模糊隶属函数,考虑到状态评估值的意义,其值越接近0,则状态为“良好”的置信度越高,而越接近1,则状态为“危险”的置信度越高。据此构造模糊隶属函数,如图3所示。

采用最大隶属度原则作为状态等级判别标准,因此各评语隶属函数的交点对应的评估值即为状态等级划分阈值。在确定划分阈值后,即可对装备状态等级进行判断,进而做出维修决策。

3 状态评估实例分析

本文采用油液中多类元素的浓度样本,对某型装备的变速箱技术状态进行评估,以验证本文方法的有效性。共采集得到来自24台变速箱的48个样本,其中“良好”、“劣化”和“危险”样本各16例,变速箱的真实状态通过采样后的分解检测获得,部分归一化数据如表1所示。

采用粗糙集属性约简算法对表1中的特征参数进行简约。对样本进行离散化处理得到相容决策表,运用区分矩阵算法[14],对决策表进行约简求核,得到核为{铁,铅,硅,钠,磷,锌},因此对样本进行裁剪得到新的样本集,利用这6类参数对变速箱状态进行静态评估。

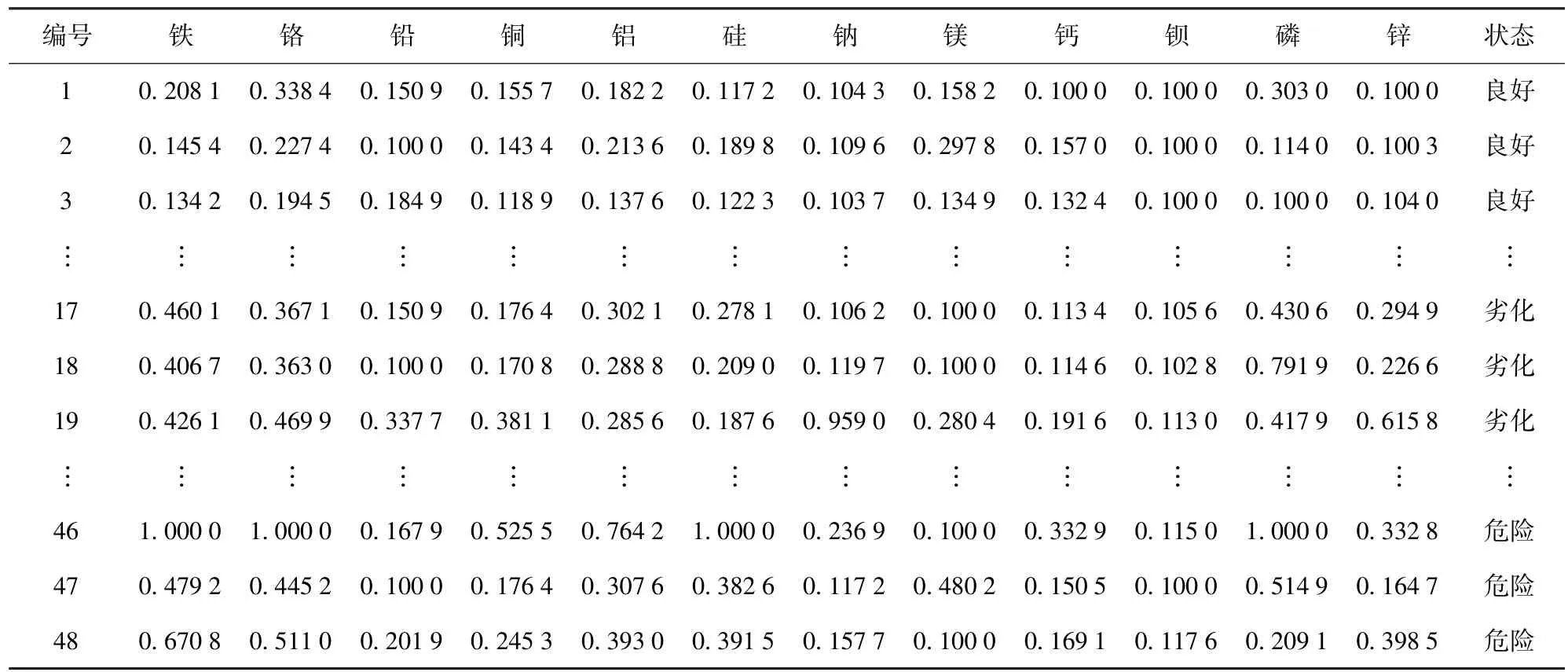
表1 某型装备变速箱油液中各类元素浓度数据Tab.1 Metal content samples of gear box lubricating oil of an equipment

按照第2节提出的变尺度混沌优化算法,对特征参数的权重进行优化。设置运算次数为50,求得历次运算Min(F)值和对应混沌优化解如图4和图5所示,Min(F)最小时求得的优化解即为最优权重。

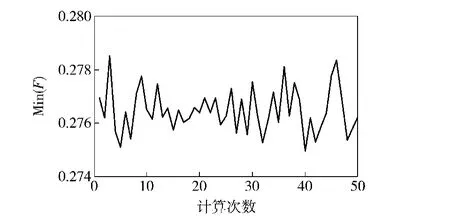
图4 历次运算Min(F)输出值Fig.4 Output results of Min(F)

特征参数最优权重向量为(0.529 4,0.000 1, 0.275 1,0.003 3,0.111 4,0.080 7),由于铅和钠元素浓度这两类参数权重很低,因此将这两类数据剔除,对特征数据加权求和,得到“良好”、“劣化”和“危险”3类样本的静态评估值如图6所示。

运用2.3节提出的模糊评判准则得到状态划分阈值分别为0.277 9和0.446 8,据此对变速箱状态等级进行判断,正确率为89.58%,评估效果不够理想。因此,对样本数据按照采样时间进行排序,将样本数据与上一个采样点的样本数据相减,求得特征参数平均劣化速度,作为对应样本的劣化速度数据进行动态评估。

利用铁、硅、磷、锌元素浓度的数据构造劣化速度向量,对样本进行归一化处理得到与各样本相对应的劣化速度数据。将状态为“良好”与“危险”等级向对应的劣化速度样本提取出来,建立聚类样本集。运用NSD-WKFCM算法进行聚类分析,算法的参数设置为:聚类数C=2、平滑参数m=2、邻近范围域阈值e=1,σ=0.301 6,迭代截止误差ε=10-6和最大迭代次数T=50.通过计算“良好”和“危险”状态下劣化速度样本的类内均值,对聚类中心进行初始化,得到2×4维初始聚类中心Vi:

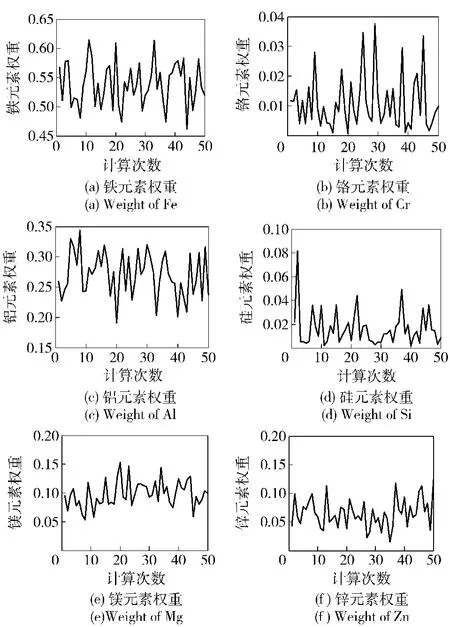
图5 各特征参数的权值Fig.5 Optimized weights of characteristic parameters

图6 样本静态评估结果Fig.6 Statically evaluated results

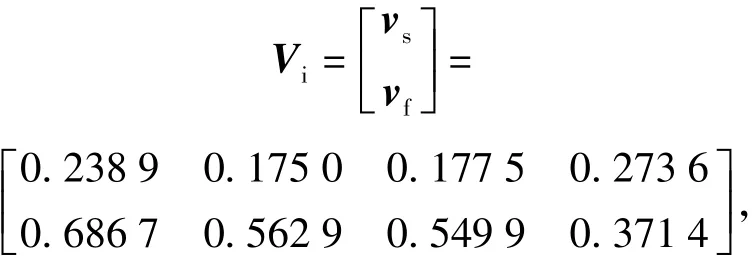
按照第2.2节提出的迭代步骤进行聚类求解,得到最优的聚类中心为

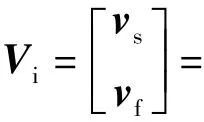
控制参数b的取值范围设为[0,4],步长为0.01,求解动态评估模型的性能随b的变化曲线,对b进行优化。计算b取固定值时的σn/un、σd/ud、σf/uf和状态判断错误率,得到图7和图8所示的变化曲线。

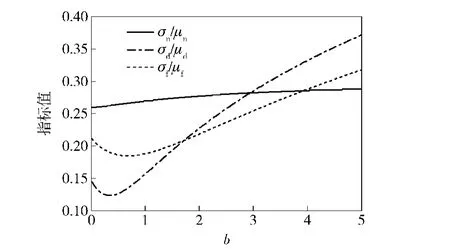
图7 σn/un、σd/ud、σf/uf的变化曲线Fig.7 Curves of σn/un,σd/udand σf/uf

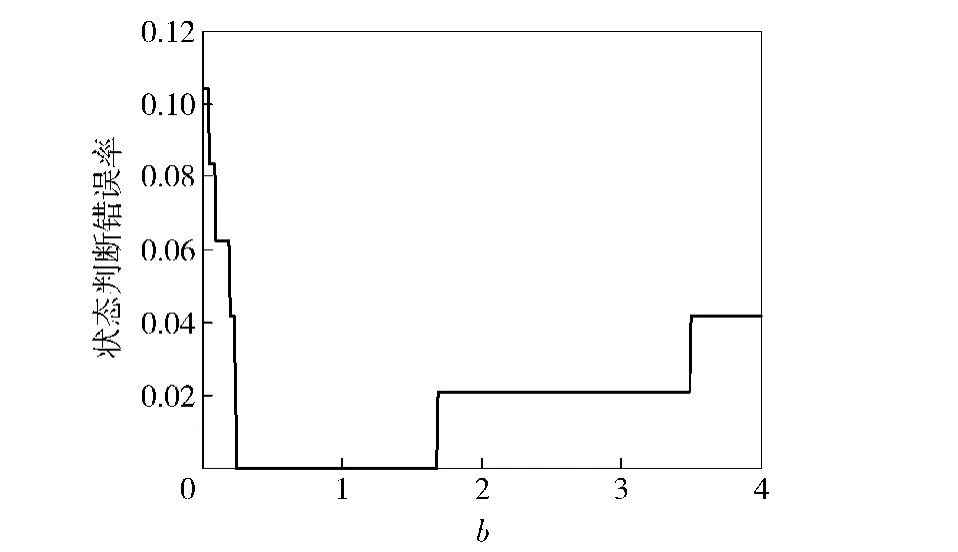
图8 状态判断错误率的变化曲线Fig.8 Curve of condition judgment mistake rate

上述4类指标值越小则评估效果越好,因此综合分析各指标曲线,确定b=0.5,代入(8)式确定最优的动态调整函数。将动态调整函数与静态加权公式相乘得到完整的动态评估模型,对样本进行动态评估,得到的评估结果如图9所示。

由图9可知,“良好”和“劣化”状态的划分阈值为0.319 7,“劣化”和“危险”的划分阈值为0.557 7,此时样本状态判断正确率达到了100%,与静态评估89.58%的正确率相比有显著提高,可见动态评估能够有效地弥补静态评估方法的不足,更加准确地判断装备状态。

4 结论

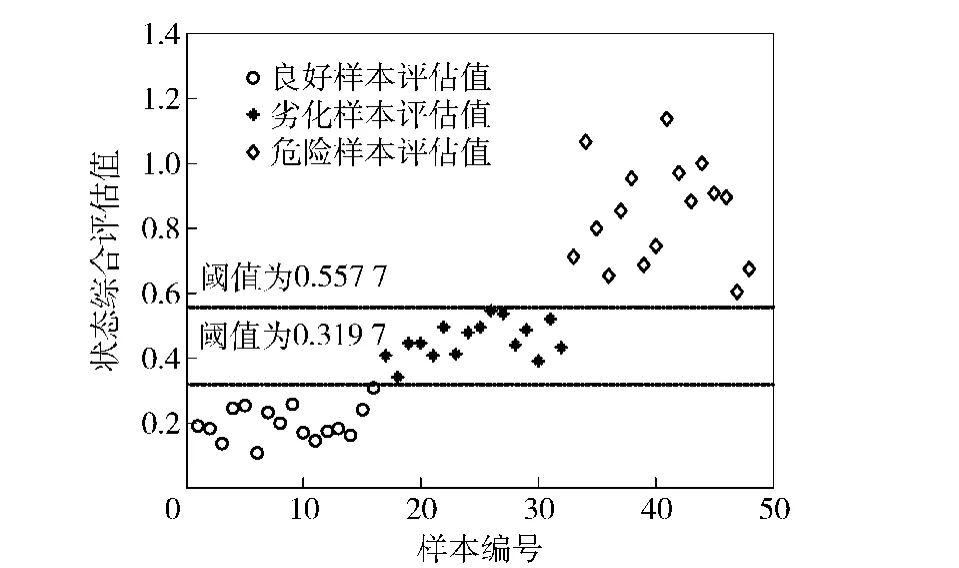
图9 样本动态评估结果Fig.9 Dynamically evaluated results

本文利用多维状态特征信息对装备状态进行评估,建立了融合静态观测信息与劣化速度信息的动态评估模型。采用变尺度混沌优化算法对高维、含噪条件下基于目标函数的状态静态评估建模方法进行研究,增强了静态评估的客观性,提高了状态评判的准确率。针对状态指标劣化信息未得到有效利用的问题,本文通过构造动态调整函数对静态评估模型进行修正,在合理描述装备状态劣化共性趋势的同时,充分发掘了个体装备时序特征观测值的隐含信息,进一步提高了装备状态评判的准确率。因此,

装备动态评估模型能够准确地评估装备状态,为实施状态维修提供信息支持。

References)

[1] 李爱民,张耀辉,张仕新.装甲车辆工况监测参数的选择[J].装甲兵工程学院学报,2006,20(4):32-35.

LI Ai-min,ZHANG Yao-hui,ZHANG Shi-xin.Selection of working condition detecting parameters for armored vehicles conditionbased maintenance[J].Journal of Academy of Armored Force Engineering,2006,20(4):32-35.(in Chinese)

[2] 陈小卫,王文双,宋贵宝,等.基于模糊偏序关系的混合型多属性决策方法[J].系统工程与电子技术,2012,34(3):529-534.

CHEN Xiao-wei,WANG Wen-shuang,SUN Gui-bao,et al.Hybrid multi-attribute decision making based on fuzzy preference relation [J].System Engineering and Electronics,2012,34(3):529-534.(in Chinese)

[3] 潘玉娜,陈进,李兴林.基于模糊C-均值的设备性能退化评估方法[J].上海交通大学学报,2009,43(11):1794-1797.

PAN Yu-na,CHEN Jin,LI Xing-lin.Fuzzy C-means based equipment performance degradation assessment[J].Journal of Shanghai Jiaotong University,2009,43(11):1794-1797.(in Chinese)

[4] 吴笛.基于BP神经网络的航天发射平台性能评估研究[J].机床与液压,2011,39(17):144-148.

WU Di.Research on performance estimation of aerospace launch platform based on BP neural network[J].Machine Tool&Hydraulics,2011,39(17):144-148.(in Chinese)

[5] 张黎明,赵新文,蔡琦.基于SVM的核动力屏蔽泵老化状态评估[J].核动力工程,2011,32(2):124-127.

ZHANG Li-ming,ZHAO Xin-wen,CAI Qi.Evaluation on aging state of NPP canned motor pump based on SVM[J].Nuclear Power Engineering,2011,32(2):124-127.(in Chinese)

[6] 孙宜权,张英堂,李志宁,等.基于核主成分分析的柴油机技术状态评估[J].车用发动机,2012(2):89-91.

SUN Yi-quan,ZHANG Ying-tang,LI Zhi-ning,et al.Evaluation of diesel engine technical state based on KPCA[J].Vehicle Engine, 2012(2):89-91.(in Chinese)

[7] 胡庆春,王洋,张继权,等.基于灰熵的变压器绝缘状态评估[J].电力科学与工程,2011,27(10):16-22.

HU Qing-chun,WANG Yang,ZHANG Ji-quan,et al.Method for insulative condition classification evaluation of power transformer based on gray entropy[J].Electric Power Science and Engineering,2011,27(10):16-22.(in Chinese)

[8] 郭保伟,李书明.基于模糊层次分析法的民航发动机状态评估[J].装备制造技术,2012(12):160-162.

GUO Bao-wei,LI Shu-ming.State assessment for civil aviation engine based on FAHP[J].Equipment Manufacturing Technology, 2012(12):160-162.(in Chinese)

[9] 修春波,刘向东,张宇河.双混沌机制优化方法及其应用[J].控制与决策,2003,18(6):724-726.

XIU Chun-bo,LIU Xiang-dong,ZHANG Yu-he.Optimization algorithm using two kinds of chaos and its application[J].Control and Decision,2003,18(6):724-726.(in Chinese)

[10] 李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.

LI Bing,JIANG Wei-sun.Chaos optimization method and its application[J].Control Theory&Applications,1997,14(4): 613-615.(in Chinese)

[11] 邹恩,陈建国,李祥飞.一种改进的变尺度混沌优化算法及其仿真研究[J].系统仿真学报,2006,18(9):2426-2432.

ZOU En,CHEN Jian-guo,LI Xiang-fei.Improving mutative scale chaos optimization algorithm and simulation study[J].Journal of System Simulation,2006,18(9):2426-2432.(in Chinese)

[12] LIU X F,YANG C.Clustering performance of different density function weighted FCM algorithm[C]∥Proceeding 2010 6th International Conference on Natural Computation.Yantai:IEEE, 2010:3296-3300.

[13] 刘小芳.基于核理论的遥感图像分类方法研究[D].成都:电子科技大学,2011.

LIU Xiao-fang.Research on remote sensing image classification methods based on kernel theory[D].Chengdu:University of E-lectronic Science and Technology of China,2011.(in Chinese)

[14] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001.

WANG Guo-yin.Rough set theory and knowledge acquisition[M]. Xi'an:Xi'an Jiaotong University Press,2001.(in Chinese)

Dynamic Evaluation Methods for Equipment Technical Condition Based on Multi-dimensional Characteristic Parameters

WANG Shao-hua,ZHANG Yao-hui,HAN Xiao-hai
(Department of Technology Support Engineering,Academy of Armored Force Engineering,Beijing 100072,China)

According to the fact that current condition evaluation models lay more emphasis on the static observations of characteristic parameters and less on trend information inherent in sequential observations, a new condition evaluation model with static and dynamic evaluations is proposed.For the weighting of multi-dimensional characteristic parameters,a mutative scale chaos algorithm is applied to achieve optimal objective weighting,and a static condition evaluation model is established.Based on static evaluation,a“distance”which measures real-time deteriorating speed and standard deteriorating speed is opted to modify the static evaluation result.NSD-WKFCM(neighbor sample density weighted kernel fuzzy C-means)clustering algorithm is used to solve standard vector of deteriorating speed.A dynamic adjusting function based on“distance”combined with its parameter optimization algorithm is proposed,and the complete dynamic condition evaluation model is established.A case study is performed to verify the effectiveness of the model.

ordnance science and technology;multi-dimensional characteristic parameter;chaos optimization algorithm;NSD-WKFCM clustering algorithm;dynamic evaluation

E075

A

1000-1093(2014)11-1883-08

10.3969/j.issn.1000-1093.2014.11.021

2013-12-17

军队“十二五”预先研究项目(51327020303)

王少华(1986—),男,博士研究生。E-mail:aafe77330@163.com;

张耀辉(1960—),男,教授,博士生导师。E-mail:zyh532@sohu.com