主从式无人水面艇协同定位滤波方法与实验验证

徐博,肖永平,高伟,刘亚龙,杨建

(1.哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001;2.陕西航天导航设备有限公司,陕西宝鸡 721006)

主从式无人水面艇协同定位滤波方法与实验验证

徐博1,肖永平2,高伟1,刘亚龙1,杨建1

(1.哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001;2.陕西航天导航设备有限公司,陕西宝鸡 721006)

多无人水面艇(USV)协同导航定位技术是解决复杂作业环境下导航问题的重要途径。针对单主艇的主从式多USV的协同导航定位问题,建立了协同定位的状态空间模型,然后将非线性模型绕滤波值展开,得到非线性系统的线性化模型;利用扩展卡尔曼滤波算法进行信息融合;针对双艇间的距离、角度与协同定位精度的关系展开研究,对协同导航滤波算法使用李代数法进行了可观测性分析。研究表明,控制相邻两时刻主从艇之间距离和角度变化量是提高协同定位精度的有效措施。通过仿真和实验验证,为下一步深入研究和路径规划奠定了基础。

控制科学与技术;无人水面艇;测距;协同定位;扩展卡尔曼滤波

0 引言

无人水面艇(USV)也叫水面无人艇,实际上是一种水面无人平台,主要用于执行危险或复杂环境下以及不适于载人艇执行的复杂任务,例如资源勘探和水文地理监测等。同时,近些年来USV在军事上也广为应用,在无人艇上配备先进的控制设备、传感器系统、通信和武器系统之后,可以执行侦察、搜索、排雷和搜救等任务,在反潜作战、反特种作战和打击海盗等领域也有着巨大的作用。

在现代海洋资源开发和军事任务中,常常面临着复杂的情况,需要多艘无人艇协同作业才能够完成,而导航是实现协作的基础,因此研究多无人艇的协同定位导航有着巨大的理论价值和实际作用。协同单元相互合作不仅可以节省整体工作时间,还能够避免编队中全部单元均装备高精度仪器所造成的费用过高问题。通过USV间的相互合作可以建立一个稳定的指挥系统;另一方面,未来战争单兵作战的机会将大大减小,取而代之的是多系统的协同指挥。

随着协同作战应用需求的提升,协同导航算法研究逐步成为热门。20世纪90年代日本科学家Kurazume等在研究多机器人定位时首次提出了协同定位的概念[1]。这一理论的提出引起了导航领域学者的极大兴趣,随着定位和导航技术在各个应用领域中发挥的作用逐步加大,基于位置服务的军用价值和商业价值也逐步扩大[2]。随着各国学者在协同导航相关方面的进一步研究,使得协同导航在卫星导航、机器人以及水下航行器等多个领域都取得了一定成果。其中,美国Minnesota大学以Roumeliotis为首的研究小组开展了一系列机器人协同定位基础理论研究,如可观测性分析、误差分析、估计一致性分析、队形优化研究等[3]。美国麻省理工学院的Leonard研究团队对水下航行器的协同定位进行了基于水面皮艇和不基于水面皮艇的算法研究[4]。

欧盟最近资助某科研团体进行名为GREX项目的研究,也在对协同定位进行研究,他们的主要目的是通过某种软件来协调多艘多用途自主水下航行器(MAUV)的行动。将MAUV看作一个中转站,将来自主艇的信息通过网络传递给其他MAUV,其通信距离可达到英里级别[5]。

美国L-3通信公司下属的Interstate Electronics Corp研究了地球同步卫星协同导航的分散式算法,同时L-3通信公司资助悉尼大学自主系统研究中心以机器人协同导航为背景,研究了相关的协同算法[6]。

美国麻省理工学院的“CRADE”系统采用通信导航辅助的多无人水下航行器(UUV)协同定位方法[7]。这个多UUV系统包括一些装备有高精度惯导系统和多普勒测速仪、专用于通信和导航的辅助航行器,帮助其他低精度航行器进行通信与定位。

美国的Curcio等提出了一种基于Kullback-Leiber的单主艇协同导航算法,并做了大量的水上试验[8];Baccou等为了解决单主艇协同导航求解不充分的问题提出了通过主艇、从艇之间的机动来提高协同导航的定位精度[9];Singh等提出了单程测距技术,解决了双程测距中时间延迟而造成的测距精度下降的问题,且可以任意扩展艇的数量[10]。

Bahr[11]和国内西北工业大学协同定位研究小组[12-17],则采用相邻时刻的运动矢径作为观测量来实现单主艇协同定位。国内学者王玲等对多机器人群在未知环境中进行协同、合作定位的技术进行了深入研究,基于相对测量和自身的运动,建立了系统模型,并且由此借助扩展卡尔曼滤波(EKF)算法来融合运动信息和相对观测信息,给出了定位机器人群中每个机器人的滤波方程[18-19]。

综上所述,国内外学者针对机器人和水下潜器进行了相关的研究工作,但是对于水面艇协同导航的研究尚处于起步阶段。根据主艇数目的不同,主从式无人艇的协同定位研究分为基于双主艇和基于单主艇两大类。基于双主艇的协同方案定位精度相对较高,但是所需信息量大,且对双艇信息的同步性要求很高,相比来说基于单主艇的系统需要的融合信息更少,系统计算量较小,具有更强的应用价值。本文研究利用EKF算法来提升USV协同定位的精度,并分析了其可观测性问题,具有较强的理论价值和实际意义。

1 协同定位方案

多USV协同定位基于地面移动机器人的思想,通过定位信息传递与相对距离测量实现协同定位。多艇协同定位时,艇间是通过水声通信装置发送彼此的位置信息并同时测量通信双方的相对距离,通过信息融合对自身定位进行修正,提升无人水面艇的定位精度。多水面艇协同定位采取基于概率学的滤波定位算法,针对多USV编队的定位问题,应用EKF算法提高USV定位的精度,达到预期效果。多USV的协同定位方式主要为:并行式(系统中每个USV的功能和结构完全相同)和主从式(系统中有一个携带有高精度捷联惯性导航系统和多普勒测速仪等设备的艇担任主艇,而在其他艇上装备成本低、精度低的惯导系统)。

协同定位原理如图1,从艇向主艇发送测距请求信号,主艇接收到测距请求信号后通过水声传播发出与到达的时间差来计算出相对距离以及通过水声调制解调器以广播的形式向从艇发送主艇的位置信息以及相互之间的距离信息,然后从艇就可以通过一定的滤波算法来校正从艇的位置信息,达到提高从艇导航精度的目的。

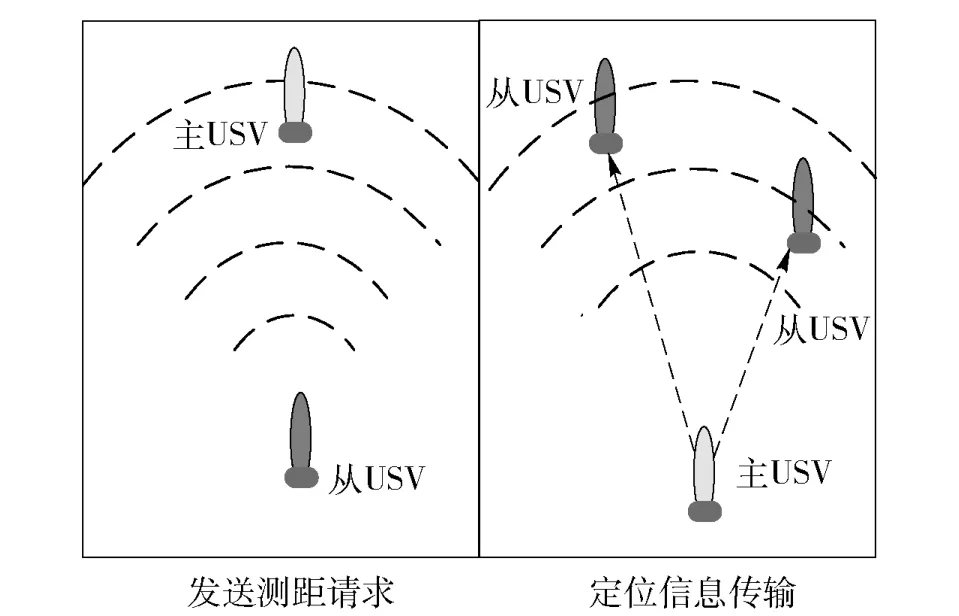
图1 协同定位原理图Fig.1 Principle of cooperative localization

2 多USV系统协同定位滤波算法

2.1 多USV运动学模型建立

由于从艇自身导航设备精度较低,随着时间的增长,其定位误差不断积累,因此采用单个高精度的主艇提供精确的位置信息和测距信息来抑制误差的不断积累。

单主艇的定位方程可以表示为

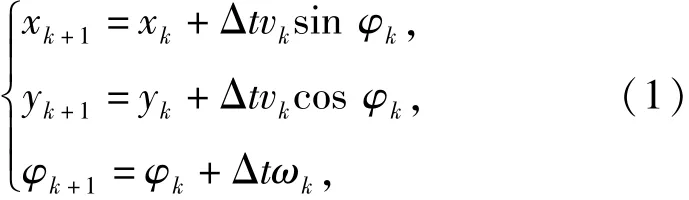
式中:xk,yk表示无人艇航推定位信息,xk表示k时刻无人艇的经度信息,yk为水面艇k时刻的纬度信息;Γt为采样周期,一般取为1 s;vk为无人艇的前向合成速度;φk表示无人艇航向角;ωk表示k时刻无人艇航行的角速度,均受高斯白噪声干扰。

定位方程可以简写为

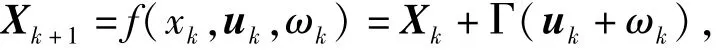
式中,Xk=(xk,yk,φk)T,表示USV在k时刻的状态; Γ(uk+ωk)为非线性项,uk=(vk,wk)T,均受高斯白噪声影响。

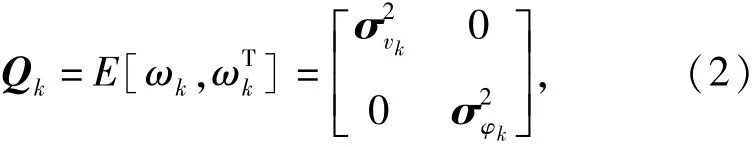
在单主艇协同定位中,由于只有一个主艇,因此可使用的信息也变少,即量测量为:主艇位置信息以及距离标量信息。因此,量测量Zk可以表示为

式中:(xMk,yMk)表示k时刻主艇的位置信息;(xSk, ySk)表示的是k时刻从艇的位置信息;rk为k时刻的距离信息;h[]表示非线性函数;主艇与从艇之间水平距离的量测噪声为零均值的高斯白噪声,其方差矩阵分别为

2.2 模型的线性化与滤波步骤

由运动学方程可知此系统为非线性系统,常规的卡尔曼滤波(KF)递推方程只适合于线性系统,因此就需要利用适用于非线性系统的EKF方程来进行处理。本文采用围绕滤波值将f[]和h[]展成泰勒级数并保留一次以下项的方法得到非线性系统的线性化模型。将f[]围绕展开,泰勒级数略去二阶以上项,得到

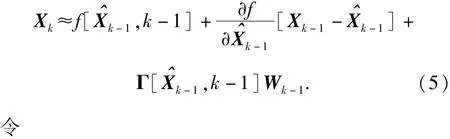
1

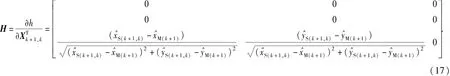
3 可观测性分析

所谓量测系统的能观测性,是指系统的初始状态可由其输出的量测值来确定的一种性能。对于如下一个线性离散时变系统:

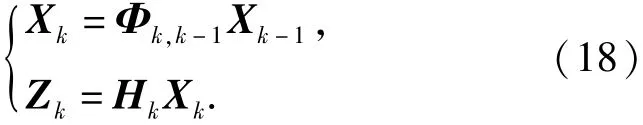
系统是否可观测的实质就是系统状态Xk能否根据一组观测值Z=[Z1,Z2,…,Zk]T来确定。根据(18)式,可以将量测和状态的对应关系写成如下矩阵形式[20]:

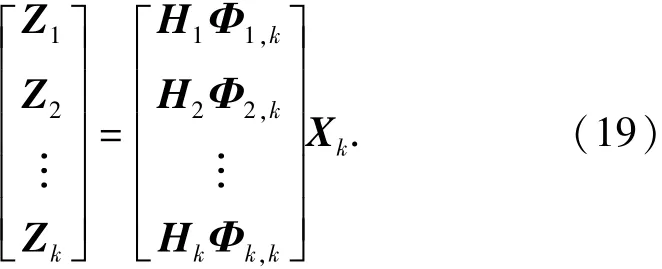
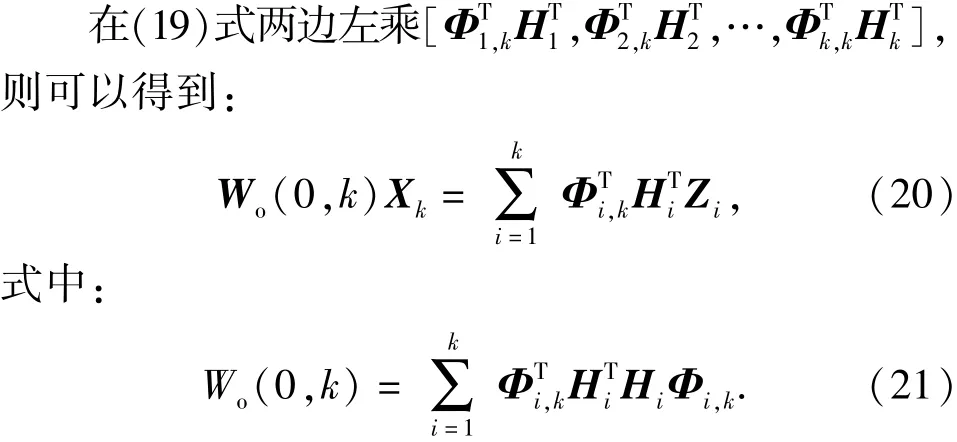
由(21)式可以看出,要想根据观测量Z1,Z2,…,Zk最终确定状态Xk,其充分必要条件是矩阵Wo(0,k)是非奇异矩阵,Wo(0,k)被定义为系统的能观测性格拉姆判别矩阵。对于单主艇协同导航离散时变系统,系统可观测判别矩阵的等价形式可以表示为

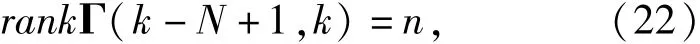
式中:Γ(k-N+1,k)为离散时变系统的可观测秩判别矩阵;n为系统状态向量维数。

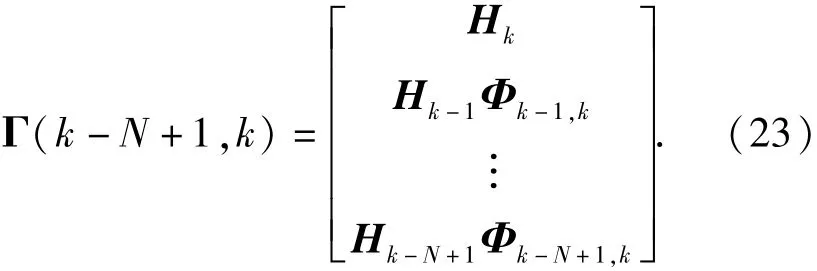
由2.1节(3)式可以看出,量测量Z主要取决于第三维观测信息rk,即距离rk将主从艇联系起来,对子艇的导航误差信息的估计起决定性作用。对于此一维观测信息Z,需要至少进行N=2次观测才可能完全估计出系统的二维位置状态。根据连续两次观测数据得到系统的可观测矩阵为

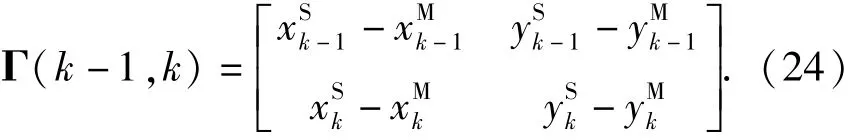
根据系统可观测性秩判别条件,系统可观测当且仅当系统可观测矩阵满秩,即系统的可观测矩阵行列式不为0,

也就是说,当且仅当相邻时刻主从USV距离向量方向相同时系统不可观测,在其他条件下均可观测。为了进一步分析系统可观测度大小与系统状态的量化对应关系,采用了基于谱条件数的可观测性分析理论,对系统的可观测性做进一步的定量分析[10-11]。

条件数反映了线性方程组AX=b(b∈Cn)的解对b的误差或不确定度敏感性的度量,其中A为方程组的系数矩阵。如果A的条件数越小,则b的微小改变引起解X的改变越小,因此数值稳定性也越好。

当N=2时,cond(A)2为2范数(谱范数)的条件数,简称为谱条件数[12]。矩阵的条件数越小,矩阵越趋于良态,数值稳定性越好;反之,矩阵越病态,数值稳定性越差。因此可以通过观测矩阵条件数的大小来确定系统的可观测性强弱。由于恒有cond(A)≤1,因此将可观测矩阵谱条件数的倒数定义为系统的可观测度,表示为式中:dk为k时刻主从USV二维平面直线距离。令θk为k时刻主从USV距离向量方位角,则观测矩阵可以进一步表示为

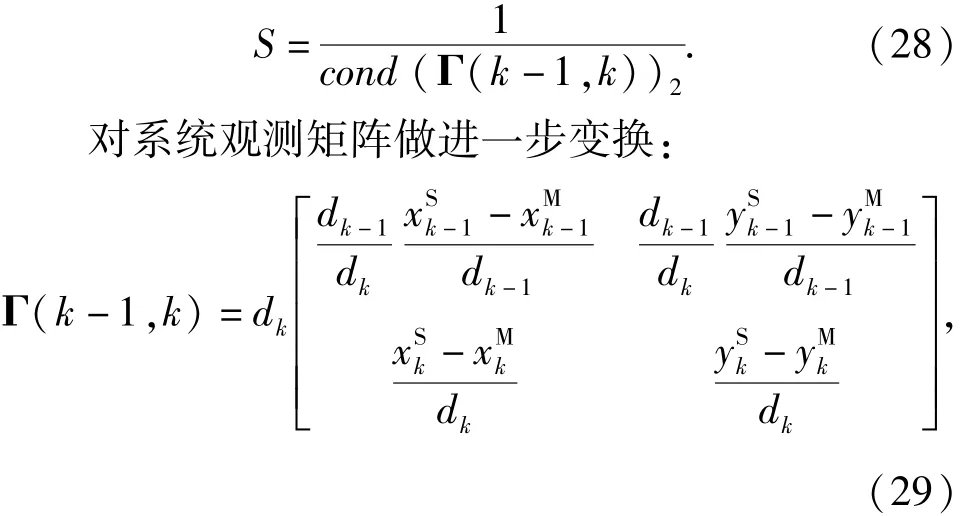
从(31)式可以看出可观测度大小主要由相邻时刻主从USV距离比γ以及相邻时刻主从USV距离向量方位变化Γθ来决定,因此当γ确定时就可以得到可观测度S与Γθ的关系,同理当Γθ确定时就可以得到可观测度S与γ的关系,如图2和图3所示。

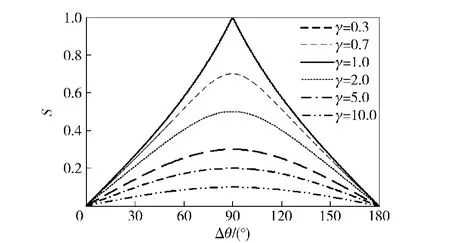
图2 S与Γθ之间的关系Fig.2 The relation between S and Γθ

从上述理论推导和仿真图可以得到:

1)从图2可以看出,无论γ如何取值,系统可观测度S随着Γθ的变化先增大,后减小,并且在Γθ=90°处取得极大值,并且曲线以90°为轴,左右两边基本对称。

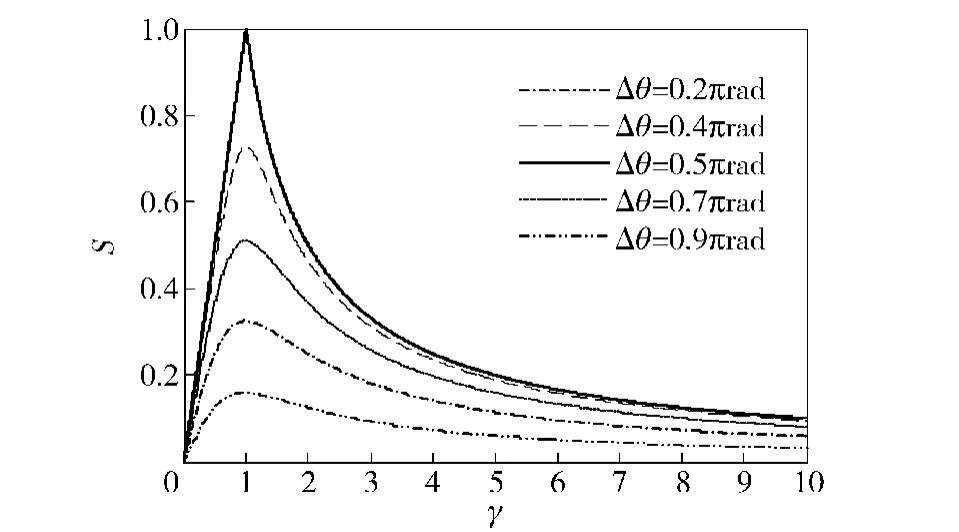
图3 S与γ之间的关系Fig.3 The relation between S and γ

2)从图3中可以看出,无论Γθ如何取值,系统可观测度S随着γ的变化先增大,后减小,并且在γ=1处取得极大值,在其左右两侧曲线呈现出强烈的不对称性和非线性。0＜γ＜1时,越接近0,可观测度下降越快。大于1时,可观测度的变化相对要慢,而且当其大于一定数值的时候,所引起的可观测度的变化变得非常缓慢。

3)系统可观测度S在Γθ=90°、γ=1处取得极大值,当滤波周期取为1 s的情况下,即主从艇间以角速度为90°/s做匀速圆周运动时,系统可观测性最好。

4 仿真分析

为检验算法的可靠性和实用性,本文进行仿真分析,设置如下:

1)主艇起始坐标(10 m,10 m),初始航向角为0°,航速为8 kn,角速度为0.05°/s.从艇起始坐标(0 m,0 m),初始航向角为30°,航速为10 kn,航行30 min之后航向角变为90°,速度保持不变。状态更新周期Γt=10 s,仿真时长为180 s.

图4～图7给出了从艇运动过程中航位推算(DR)得到的定位误差和基于EKF算法得到的协同定位误差。由图中可以看到:

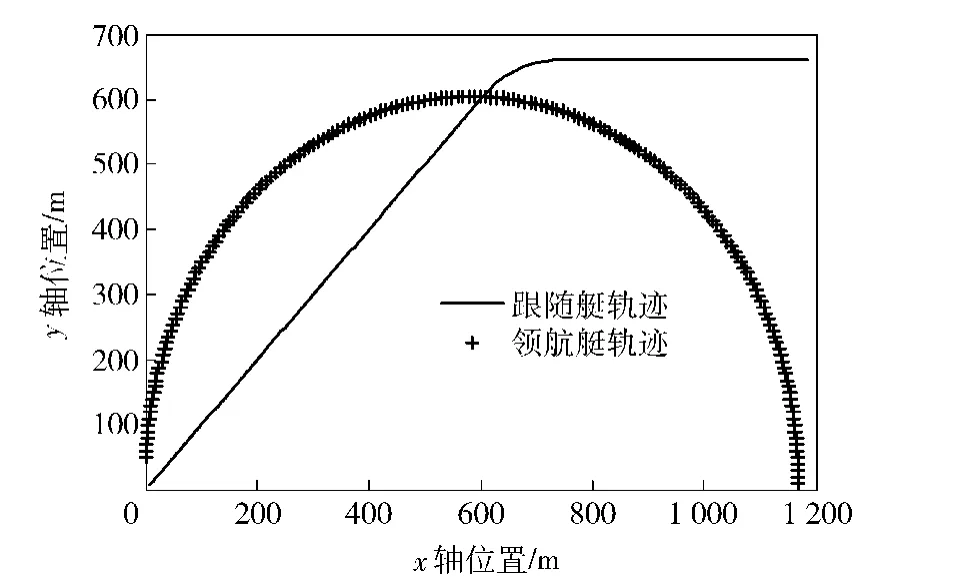
图4 真实轨迹示意图Fig.4 Real Tracks

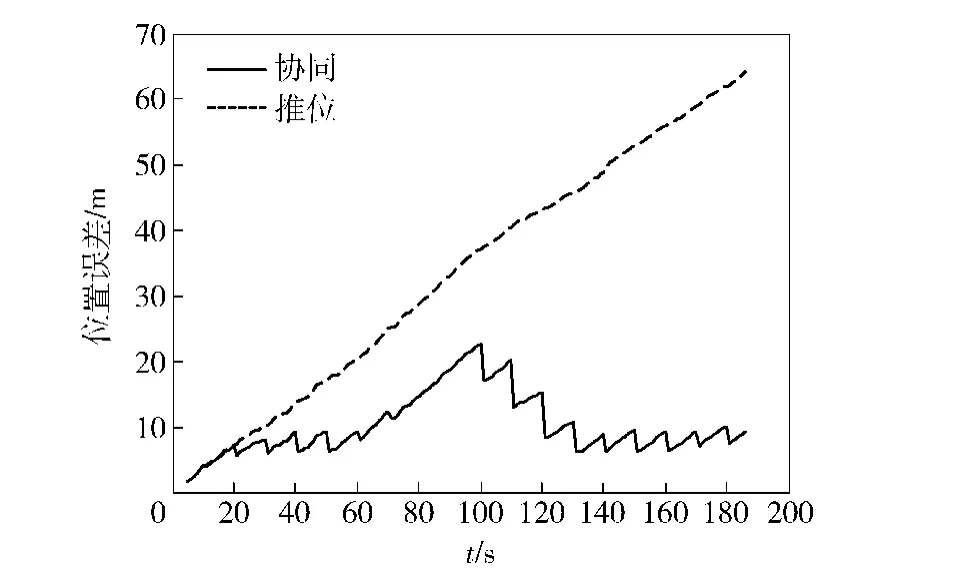
图5 定位误差比较图Fig.5 Locating errors

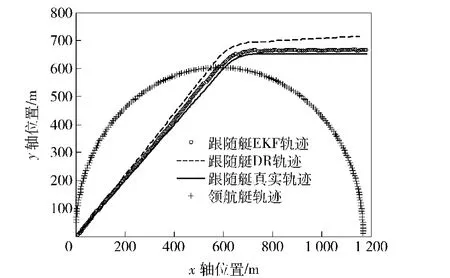
图6 从艇航迹比较图Fig.6 Tracks of slave USV

1)图6中虚线表示航位推算的轨迹,空心圆线表示协同导航求得的轨迹,实线表示真实轨迹。由图6可知,当从艇只采用自身的捷联惯导系统和多普勒测速仪航位推算时,求得的位置明显偏离真实轨迹,其整体的定位误差不断增大。

图7 从艇航迹比较局部放大图Fig.7 Tracks of slave USV(enlarged)

2)EKF算法较航位推算在x轴和y轴方向都有明显的提高。当主艇、从艇按照图4所示的轨迹运动时,由于两艇运动方式差别较大,所以可以认为在相邻测距的方向不同,系统可观测性强,协同定位精度高。

3)当主艇改变其航向角时EKF算法的误差有一定的波动,这表明主艇航行的轨迹突变对从艇定位精度也有较大的影响(因为当USV改变其航向角时,用于航位推算的运动学模型与USV的真实动力学模型之间存在失配,再加上从USV配备的设备精度较低,导致它的定位误差快速增长),这为以后实际应用中如何设定主从航行轨迹作出启示,即尽量保证主从艇的航向不发生突变。

图8从可观测性角度对仿真结果进行了分析。当主艇、从艇按照图4所示的轨迹运动时,两艇较大的运动方式差别使得系统可观测性较强,反映在EKF算法上使得到的协同定位误差较小。100 s处主艇航行的轨迹突变,系统可观测性也大幅度降低,带来较大的滤波误差,使协同定位精度变差。随后无较大轨迹突变,系统可观测性逐渐恢复,协同定位误差也逐渐变小。

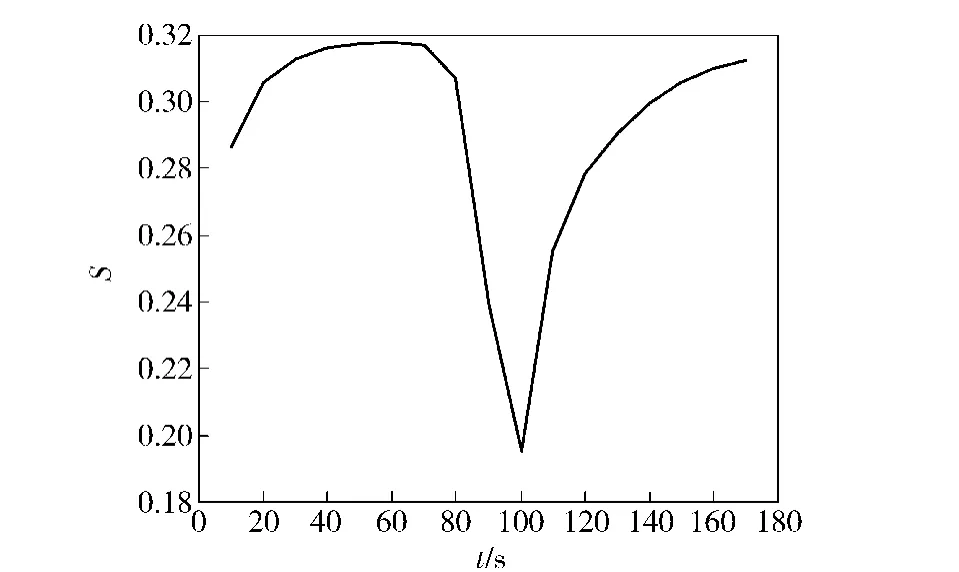
图8 系统可观测性仿真图Fig.8 Simulation diagram of system's observability

为了更清晰地描述EKF算法的定位效果,表1给出了t时刻EKF算法和航位推算算得的从艇位置误差信息。从表中可以更加直观地看出,EKF算法比DR算法所得到的位置误差更小。

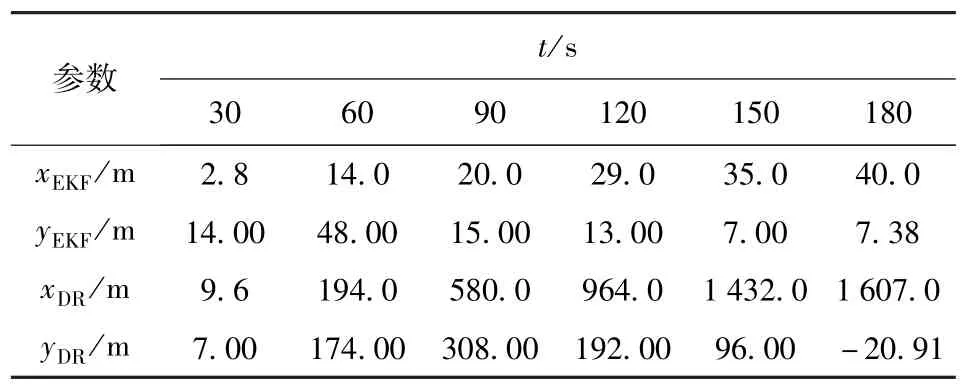
表1 t时刻从艇位置误差Tab.1 Location errors of slave USV

5 水上实验验证

为了验证本算法的有效性,在无锡太湖以水面小艇为载体进行了水上实验。针对于不同机动方式进行了测试,进一步验证了上述理论和仿真的正确性。

主艇上配备GPS、水声通信设备(验证本算法不需要使用主艇上的多普勒计程仪),从艇上配备MEMS微机械惯性导航系统、DVL计程仪以及水声通信设备,两艇之间通过水声设备完成测距与通信。所用设备及其数量如表2所示,实验设备现场如图9所示。

表2 实验设备Tab.2 Experimental equipment

上述设备中,水声测距误差为1 m,GPS定位精度为2 m,DVL计程仪测速误差1%,MEMS惯性系统输出精度5°/h.

实验步骤如图10所示。

步骤1,主艇的计算机时钟调为同步,精确调到秒级。

步骤2,从艇通过MEMS输出的航向角和GPS导航系统输出的速度进行航迹推位。

图9 实验设备现场Fig.9 Site of experimental equipment

步骤3,主艇向从艇发出自身的位置信息。

步骤4,从艇通过自身的GPS位置信息和收到的主艇的GPS位置信息计算出和主艇的距离,作为观测量,使用EKF算法计算航迹的估值,并和GPS输出的航迹进行比较。

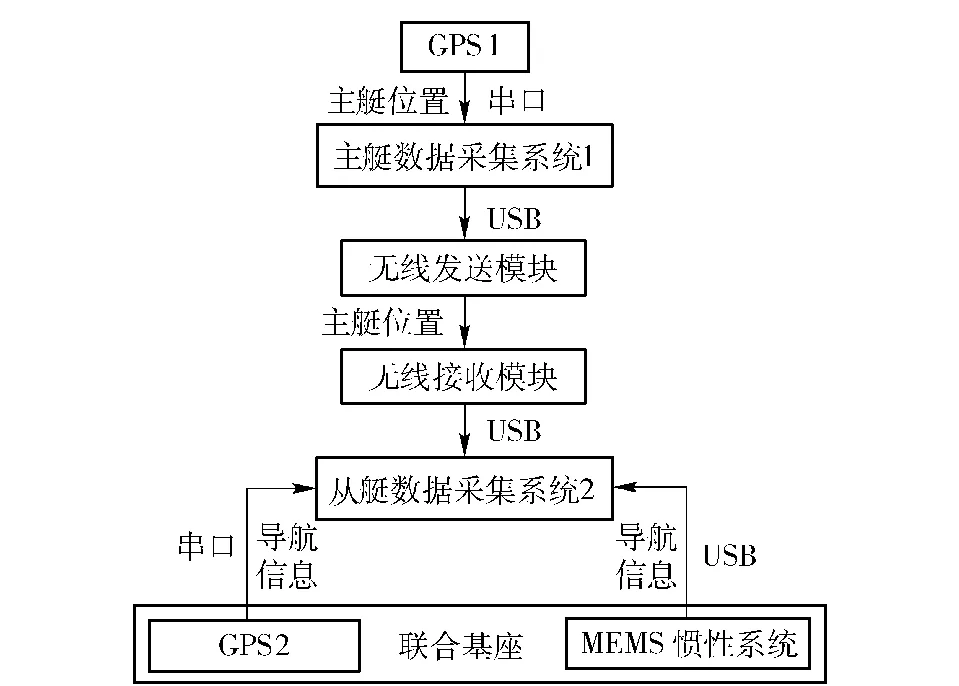
图10 实验步骤示意图Fig.10 Experimental Procedure

实验共进行2 000 s.在实验中,主艇起点为31°25′16″N,120°8′14″E,从艇起点为31°25′19″N, 120°8′35″E.两艇同时起航,做近似平行的并排前进运动。1 400 s后,从艇停止运动,终点为31°26′1″N, 120°8′13″E,同时主艇继续围绕从艇做半径为170 m左右的圆周运动。2 000 s后主艇停止,主艇终点为31°25′55″N,120°8′11″E.以这两组典型运动状态数据为样本,针对协同导航算法进行了验证,两组运动轨迹(圆周运动和并排前进)如图11所示。

所对应的航位推算误差和协同导航滤波算法误差曲线如图12所示。

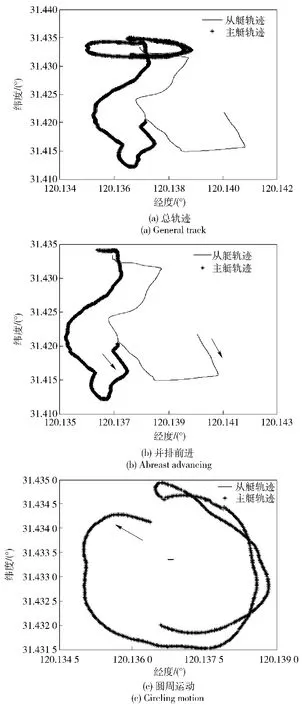
图11 主从艇运动轨迹图(圆周运动和并排前进)Fig.11 Tracks of USVs

综合图11、图12可以看出,双艇运动的相对位置关系对协同导航的定位精度影响很大。前1 400 s对应于两艇做并排前进运动,协同定位误差小于组合推位误差,但是滤波的效果不是很明显。1 400～2000 s,从艇静止不动,主艇围绕从艇做半径为170 m左右的圆周运动,这种运动状态下的协同定位误差迅速收敛至10 m以内,协同定位效果明显优于并排前行的精度。

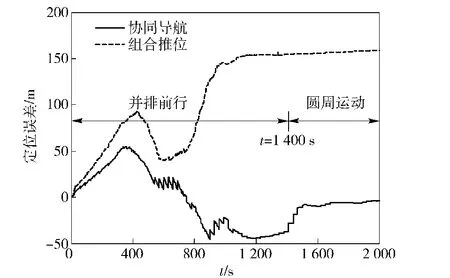
图12 从艇协同定位误差与组合推位误差比对图Fig.12 The comparison of position errors of the two methods

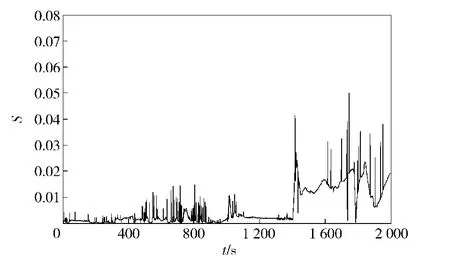
图13 协同导航系统可观测度Fig.13 Observability of cooperative navigation system

从可观测性的角度对实验结果进行分析。由图13可以看出,1 400 s之前主从艇做近似平行的并排前进运动,主从艇间相对位置变化幅度较小,因此可观测度较小,导致定位误差相对较大。与此相比, 1 400 s以后的圆周运动带来主从艇间较大的相对位置变化,使系统可观测度增加,因此定位误差大幅度减小。由此可见,主从艇不同的运动轨迹会导致可观性度的变化,进而影响协同定位精度。在协同导航过程中,需要合理设计主从艇的运动轨迹。

6 结论

本文针对多USV编队的协同定位问题给出了较实用的算法,分析了可观测性问题,并通过了仿真与实验验证。主要结论如下:

1)给出了无人艇协同导航的背景和意义;给出了算法的基本方程并介绍了无人艇协同导航建模的基础理论,之后建立系统定位模型。

2)提出EKF算法并使用Matlab进行仿真,通过设定一定的运动轨迹来实现主艇、从艇同时达到较高的定位精度。通过仿真曲线比较,本算法能够有效地提升从艇定位精度,相比航位推算所产生的误差,EKF算法能够显著地减小定位误差。

3)从可观测性角度进行了分析。研究结果表明单主艇协同定位精度与主艇、从艇之间的相对几何位置关系有很大的关系,下一步研究的重点方向是如何进行路径规划使得主艇、从艇始终处于协同导航的最佳位置。

本算法虽然通过验证,可以有效提高定位精度,但可以预见的是,在实际过程中还有许多需要考虑的问题,例如噪声问题的不确定性等。这些问题都需要在实际操作过程中去探索。本文为进一步研究多水面艇的协同导航定位问题提供了可行性思路和方法。

References)

[1] Kurazume R,Nagata S,Hirose S.Cooperative positioning with multiple robots[C]∥International Conference on Robotics and Automation.Los Alamitos,California:IEEE,1994:1250-1257.

[2] Win M Z,Conti A,Mazuelas S,et al.Network localization and navigation via cooperation[J].IEEE Communication Magazine, 2011,49(5):56-62.

[3] Hidaka Y S,Mourikis A I,Roumeliotis S I.Optimal formations for cooperative localization of mobile robots[C]∥IEEE International Conference on Robotics and Automation(ICRA).Barcelona,Spain:IEEE,2005:4126-4131.

[4] Bahr A,Walter M,Leonard J.Consistent cooperative localization[C]∥IEEE International Conference on Robotics and Automation.Kobe, Japan:IEEE,2009.

[5] Engel R,Kalwa J.Coordinated navigation of multiple underwater vehicles[C]∥17th International Offshore and Polar Engineering Conference.Bremen,Germany:IEEE,2007:1066-1072.

[6] Nicosia J.Decentralized cooperative navigation for spacecraft[C]∥2007 IEEE Aerospace Conference.Big Sky,MT:IEEE,2007: 1-6.

[7] Willcox S,Goldberg D,Vaganay J,et al.Multi-vehicle cooperativenavigation and autonomy with the bluefin CADRE system[C]∥Proceedings of International Federation of Automatic Control Conference.Oxford,UK:Pergamon Press,2006:1-6.

[8] Curcio J,Leonard J,Vaganay J,et al.Experiments in moving baseline navigation using autonomous surface craft[C]∥Proceedings of MTS/IEEE OCEANS.Washington,DC:IEEE,2005: 730-735.

[9] Baccou P,Jouvencel B,Creuze V,et al.Cooperative positioning and navigation for multiple AUV operations[C]∥MTS/IEEE Oceans 2001 Conference Proceedings.Honolulu,HI:IEEE, 2001:1816-1821.

[10] Singh S,Grund M,Bingham B,et al.Underwater acoustic navi-gation with the WHOI micro-modem[C]∥Proceedings of the IEEE/MTS OCEANS Conference and Exhibition.Boston,MA: IEEE,2006:1-4.

[11] Bahr A.Cooperative localization for autonomous underwater vehicles[R].Cambridge,MA,US:Massachusetts Institute of Technology,2009.

[12] 张立川,刘明雍,徐德民,等.基于水声传播延迟的主从式多无人水下航行器协同导航定位研究[J].兵工学报,2009, 30(12):1674-1678.

ZHANG Li-chuan,LIU Ming-yong,XU De-min,et al.Cooperative localization for multi-UVS based on time-of-flight of acoustic signal[J].Acta Armamentarii,2009,30(12):1674-1678.(in Chinese)

[13] Zhang L C,Xu D M,Liu M Y,et al.Cooperative navigation and location for multiple UUVs[J].Journal of Marine Science and Application,2009,8(3):216-221.

[14] 张立川,徐德民,刘明雍.无人水下航行器网络控制器设计[J].船舶工程,2010,32(5):30-32.

ZHANG Li-chuan,XU De-min,LIU Ming-yong.Design of networked controller for unmanned underwater vehicle[J].Ship Engineering,2010,32(5):30-32.(in Chinese)

[15] 姚尧,徐德民,张立川,等.通信延迟下的多UUV协同定位——基于航迹预测的实时更新算法[J].机器人,2011, 33(1):161-168.

YAO Yao,XU De-min,ZHANG Li-chuan,et al.Cooperative localization of multiple UUVs with communication delays-a realtime update method based on path predication[J].Robot,2011, 33(1):161-168.(in Chinese)

[16] 李闻白,刘明雍,李虎雄,等.基于单领航者相对位置测量的多AUV协同导航系统定位性能分析[J].自动化学报,2011, 37(6):724-736.

LI Wen-bai,LIU Ming-yong,LI Hu-xiong,et al.Localization performance analysis of cooperative navigation system for multiple AUVS based on relative position measurements with a single leader[J].Acta Automatic Sinica,2011,37(6):724-736.(in Chinese)

[17] 张立川,徐德民,刘明雍.基于双水听器的多自主水下航行器协同导航方法[J].系统工程与电子技术,2011,33(7): 1603-1606.

ZHANG Li-chuan,XU De-min,LIU Ming-yong.Cooperative navigation for multiple autonomous underwater vehicle based on two hydrophones[J].Systems Engineering and Electronics,2011, 33(7):1603-1606.(in Chinese)

[18] 王玲,刘云辉,万建伟,等.基于相对方位的多机器人合作定位算法[J].传感技术学报,2007,20(4):794-799.

WANG Ling,LIU Yun-hui,WAN Jian-wei,et al.Multi-robot cooperative localization based on relative bearing[J].Chinese Journal of Sensors and Actuators,2007,20(4):794-799.(in Chinese)

[19] 王玲.未知环境中基于相对观测量的多机器人合作定位研究[D].长沙:国防科学技术大学,2006.

WANG Ling.Research on multi-robot cooperative localization based on relative observation in unknown environment[D]. Changsha:National University of Defense Technology,2006.(in Chinese)

[20] 高伟,刘亚龙,徐博,等.基于双主交替领航的多AUV协同导航方法[J].哈尔滨工程大学学报,2014,35(3):1-6.

GAO Wei,LIU Ya-long,XU Bo,et al.AUVs cooperative navigation based on two leaders alternately[J].Journal of Harbin Engineering University,2014,35(3):1-6.(in Chinese)

A Cooperative Navigation Approach and Its Verification of USVs with Leader-fellower Structure

XU Bo1,XIAO Yong-ping2,GAO Wei1,LIU Ya-long1,YANG Jian1
(1.Automation Academy,Harbin Engineering University,Harbin 150001,Heilongjiang,China; 2.Shaanxi Space Navigation Equipment Co.Ltd,Baoji 721006,Shaanxi,China)

The cooperative navigation and localization technology of multi-USVs is an important way to solve the navigation problem in complex environment.For the cooperative navigation and localization of multi-USVs with leader-follower structure,a state space model of cooperative localization is built,and then a linear model is obtained by expanding the nonlinear model around filter value.An extended Kalman filter is designed to fuse the sensor information to locate the slave USV in real time.At last,the relationship among USV distances,angle and accuracy is researched,and the observability analysis of cooperative navigation filter algorithm is done with Lie algebra.The results show that the navigation accuracy is improved effectively by controlling the variations of distances and angles of leader and slave USVs between two adjacent moments,which is verified by simulation and experiment.

control science and technology;unmanned surface vessel;ranging;cooperative localization; extended Kalman filter

U666

A

1000-1093(2014)11-1836-10

10.3969/j.issn.1000-1093.2014.11.015

2013-12-13

国家博士后基金项目(2012M510083);国家自然科学基金项目(61203225);黑龙江省自然科学基金项目(QC2014C069)

徐博(1982—),男,讲师。E-mail:xubocarter@sina.com;

肖永平(1989—),男,工程师。E-mail:1160481487@qq.com