模拟不同爆炸冲击波的计算方法研究
2014-06-27周杰陶钢张洪伟潘保青
周杰,陶钢,张洪伟,潘保青
(1.南京理工大学能源与动力工程学院,江苏南京 210094;2.北京跟踪与通信技术研究所,北京 100094)
模拟不同爆炸冲击波的计算方法研究
周杰1,陶钢1,张洪伟2,潘保青2
(1.南京理工大学能源与动力工程学院,江苏南京 210094;2.北京跟踪与通信技术研究所,北京 100094)
给出了一种可获得不同爆炸冲击波的方法。利用SolidWorks软件建立了冲击波生成区域与冲击波加载空气域的几何模型,采用Hypermesh软件对模型进行映射网格划分,并赋予材料参数和状态方程,通过设计Fortran程序,将所需冲击波的压力-时间曲线,转换为单位体积内能-时间的曲线,应用修正公式对曲线进行校正,然后加载到冲击波生成区域内,最后通过LS-DYNA有限元程序计算获得所需要的平面冲击波场。采用该计算方法可以模拟获得不同爆炸冲击波,误差范围在1.0%之内。该方法为深入研究爆炸冲击波创伤效应提供了一种有效的技术途径。
爆炸力学;冲击波;数值模拟;冲击波创伤
0 引言
不同爆炸源(猛炸药爆炸、气体源爆炸及不同规模的爆炸等)依照其具体情况会产生不同效果的爆炸冲击波,其爆炸超压、正压作用时间和冲量等参数均不同。在研究爆炸冲击波的杀伤和毁伤效应时,冲击波的超压、正压作用时间和冲量等基本参数的组合效应决定了创伤效果[1-3]。著名的Bowen创伤曲线[4]及冲量-压力毁伤曲线[5],都是以爆炸冲击波的超压值和正压作用时间或冲量值为创伤指示参数。因此,如何利用有限元计算程序模拟不同爆炸冲击波,是爆炸创伤领域内比较关注的问题。
爆炸实验中,炸药尺寸、炸药密度、起爆位置和环境等因素决定了爆炸冲击波的波形,且随着目标的空间位置不同,其波形特征也要发生变化[6-7]。由于实验中爆炸冲击波受多种因素制约,因此常规的数值计算结果与实验数据存在着一定的差异。常用的LS-DYNA显式动力学分析软件,一般有两种产生冲击波的方法:一种是利用炸药库中的猛炸药(TNT)模拟理想爆炸,选用MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程,通过炸药起爆获得冲击波[8],然而此方法获得的冲击波的超压峰值和正压作用时间等参数是不可调控的;另一种方法是采用LOAD_BLAST,在实体表面(Lagrangian网格)加载冲击波的压力-时间曲线[8],这种方法虽然可以获得计算需要的冲击波波形参数,却不可以进行流-固耦合计算分析,所以应用范围十分狭窄。
Greer[9]和Thom[10]通过约束计算模型外边界上节点的运动方向和旋转方向,采用理想气体的状态方程,将温度曲线加载到冲击波生成区域内,利用LS-DYNA计算获得有效的冲击波压力曲线。但是计算时需要约束所有外边界上节点的运动方向和旋转方向,否则计算将无法进行。因为外边界上的节点受到约束,冲击波将无法透射出边界,所以不能模拟无限大区域的冲击波传播特征。文献[9-10]中没有提供直接得到复杂冲击波的方法,因此不够完整。针对这些问题,本文给出了一种改进的方法,可以计算得到所需的冲击波。
1 模型与方法
通过在冲击波生成区域内加载单位体积内能-时间(E-t)曲线和设定空气域的边界条件(反射和透射边界均可),计算获得冲击波。同时该计算模型也能应用于流-固耦合计算,克服了LS-DYNA中一般方法在计算分析爆炸毁伤问题上存在的不足。
1.1 计算模型与边界条件
采用Solidworks软件建立的几何模型由冲击波生成区域和冲击波加载空气域(以下简称:空气域)构成。为了节约计算时间,空气区域的大小为3 m× 1.5 m×0.04 m,而冲击波生成区域的尺寸为3 m× 0.01 m×0.04 m.通过Hypermesh软件对几何模型进行映射网格(六面体网格)划分,网格单元的尺寸为0.01 m,空气域的网格数为180 000,网格总数为180 120,如图1所示。

图1 计算模型Fig.1 Calculation model
图1为模拟冲击波的计算模型。设定空气域的外边界A、B、C为透射边界(也可通过约束节点的运动和旋转方向,设定为刚性边界),边界允许流体介质流出空气域,以便模拟无限大空间的效应。控制冲击波的传播方向的方法:约束计算模型的上下表面(OXY平面)的所有节点(包括空气域和冲击波生成区域)在Z轴的运动方向与绕X、Y轴旋转的方向;冲击波生成区域与空气域的接触平面(OXZ平面)共节点,并约束了冲击波生成区域余下的OXY、OXZ、OYZ平面上节点的所有运动和旋转方向。
1.2 模拟冲击波的生成原理和方法
Greer[9]和Thom[10]建立的计算模型包括:高温区域和空气域。计算模型采用理想气体状态方程pV=nRT,当相对体积V为常量时,压力p与温度T呈线性关系。将所需冲击波的压力-时间(p-t)曲线转化为温度-时间(T-t)曲线,将曲线加载到高温区域,可计算获得p-t曲线。但是由于此方法需要约束所有外边界上节点的运动方向和旋转方向,这样处理会导致冲击波无法透射出边界,也就不能模拟无限大区域效应;而采用气体线性多项式的状态方程则不需要对所有的外边界节点进行约束。故采用气体线性多项式的状态方程代替理想气体状态方程,既能获得所需冲击波,又能够有效地控制边界条件。根据气体线性多项式状态方程计算冲击波E-t曲线(设定相对体积为常量),可以将曲线直接加载到冲击波生成区域,用来模拟不同爆炸类型的冲击波。
因为测量实验中,通常所使用的压电传感器无法准确测量负压,所以本文着重研究冲击波的正压相。Friedlander冲击波的正压相特征:压力迅速升高的压力峰值p+随后以指数衰减到环境压力。Friedlander冲击波正压相的数学方程式[11]为
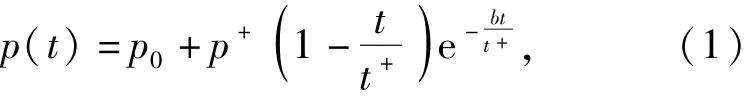
式中:p(t)为冲击波超压值的时间函数;p0为环境压力;p+为冲击波正压相的超压峰值;t+为正压作用时间;b为衰减常数。超压峰值和作用时间是由实验得来的,衰减常数根据爆炸的类型而定。
计算模型中的空气域和冲击波生成区域均采用气体的线性多项式的状态方程[8]:
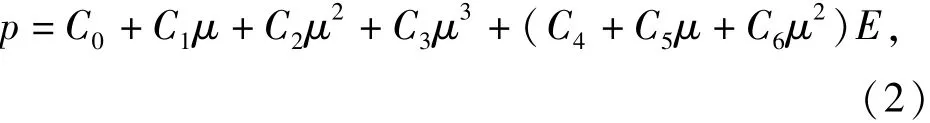
式中:p为冲击波的超压值;E为单位体积内能;μ= 1/V-1,V为相对体积。空气域和冲击波生成区域均采用空气材料模型,具体参数如表1所示。
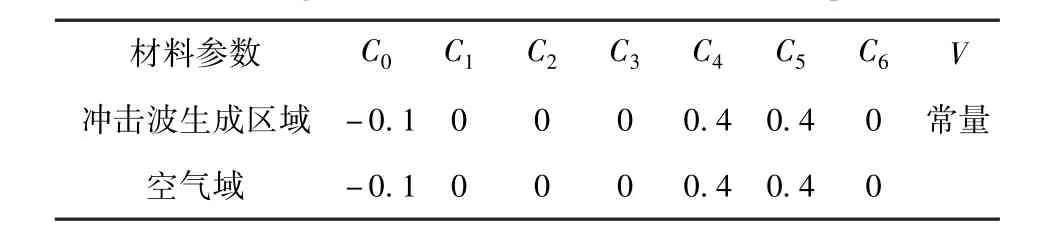
表1 冲击波生成区域和空气域的参数Tab.1 Loading area of shock wave and air basin parameters
将表1中的参数代入到(2)式中,得到冲击波生成区域和空气域的状态方程:
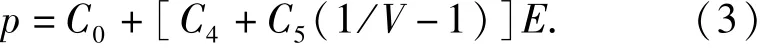
冲击波生成区域内,设定了相对体积V为常量,所以爆轰压力p与单位体积内能E呈线性关系。然而空气域中状态方程的相对体积V却不为常量,所以空气域中的冲击波压力p与单位体积内能E呈非线性关系。
Friedlander理想冲击波的模拟方法:利用Fortran程序编制Friedlander冲击波的p-t曲线。采用(3)式将冲击波的p-t曲线,转化为E-t曲线,最后将曲线加载到冲击波生成区域的K文件中;利用LSDYNA有限元程序,即可在空气域内计算获得所需的Friedlander理想冲击波。
复杂冲击波的模拟方法:采用(3)式,将复杂冲击波的实验数据(p-t曲线)转化为E-t曲线,最后将曲线加载到冲击波生成区域的K文件中;利用LSDYNA有限元程序,即可在空气域内模拟获得到复杂冲击波。
2 计算结果
2.1 计算实例
针对Friedlander理想冲击波,表2提供了所需要模拟的冲击波参数,其中超压峰值和正压作用时间参数已知。

表2 加载的冲击波参数Tab.2 Parameters of loaded shock waves
因为在LS-DYNA软件中,使用的基本单位是厘米-克-微秒制,所以设定标准状况下空气域的单位体积的初始内能为E0为25 N·cm/(g·cm3).数值计算中冲击波在空气中传播的规律,与边界条件和计算区域的大小有关;如果需要在离冲击波生成区域一定的目标位置产生冲击波,则需要依据计算模型的大小、边界条件和冲击波的传播规律,对加载的单位体积内能-时间曲线进行相应的校正。图2是模拟冲击波特征的计算结果,其中压力监控单元位于空气域中。
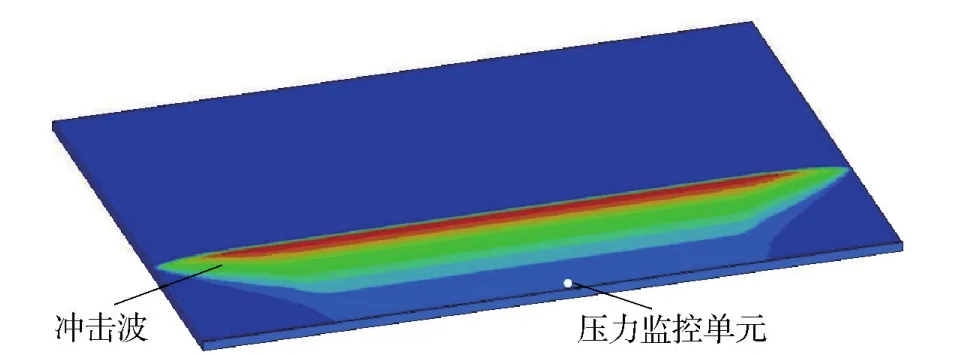
图2 计算结果Fig.2 Calculated results
由表2参数,采用Friedlander理想冲击波(1)式计算获得冲击波的p-t曲线,通过(3)式将冲击波的p-t曲线转换为E-t曲线,如图3所示;将曲线加载到计算模型中的冲击波生成区域中,利用LS-DYNA计算获得空气域内冲击波p-t曲线,如图4所示。
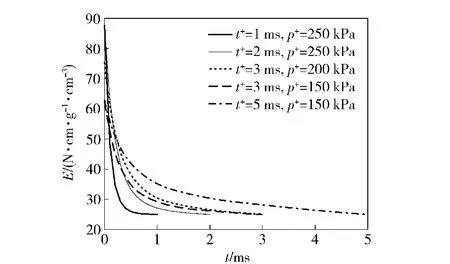
图3 加载的内能-时间曲线Fig.3 Loaded internal energy vs.time
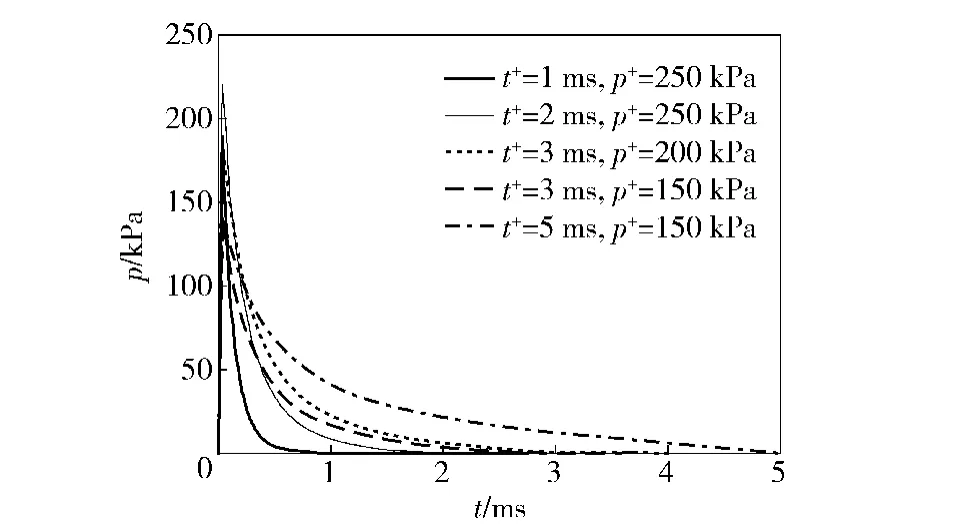
图4 冲击波的波形Fig.4 Waveforms of shock waves
通过对计算结果的分析发现:空气域内压力监控单元计算获得的冲击波正压作用时间与表2提供的冲击波正压作用时间保持一致,如图3与图4所示;但是空气域内计算获得的冲击波超压峰值p+与表2提供的冲击波超压峰值存在一定的差异,误差范围在5.3%~24%区间,如表3所示。
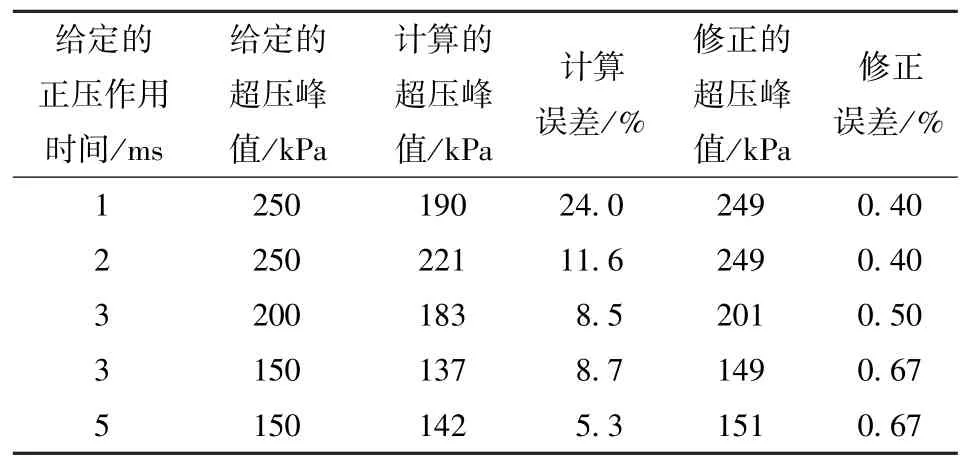
表3 冲击波超压峰值的误差分析Tab.3 Error analysis on overpressures of shock waves
计算产生误差的原因:网格的质量(数量、单元尺寸、形状)还不够高;有部分能量转化为气体的动能;冲击波由生成区域向空气域中传播时会导致能量的损失。因此在实际计算过程中需要对加载的E-t曲线进行必要的修正,采用的修正公式为

式中:EM(t)为修正后的单位体积内能;E(t)为理论计算单位体积的内能;E0为单位体积的初始内能; A为修正系数,在0.3~0.03区间。图5、图6分别为修正后的单位体积内能-时间(EM-t)曲线和修正后计算获得的冲击波波形。修正后的冲击波超压峰值与表2提供的冲击波超压峰值的误差控制在1%范围之内。

图5 修正后加载的内能-时间曲线Fig.5 Modified curves of loaded internal energy-time
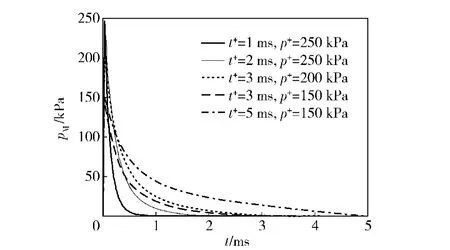
图6 修正后冲击波的波形Fig.6 Modified waveforms of shock waves
通常在复杂环境(如墙壁或有限空间)中由于冲击波反射和折射而产生混合叠加的锯齿形波形,形成复杂冲击波。本文提供的方法也适用于复杂冲击波的模拟。图7为复杂冲击波的实验曲线,将实验测得的冲击波压力-时间曲线,转换为E-t曲线,并根据修正公式校正曲线,最后将EM-t曲线加载到冲击波生成区域内,采用LS-DYNA可计算获得复杂冲击波波形。数值模拟获得的复杂冲击波波形如图8所示,压力监控单元如图2所示。
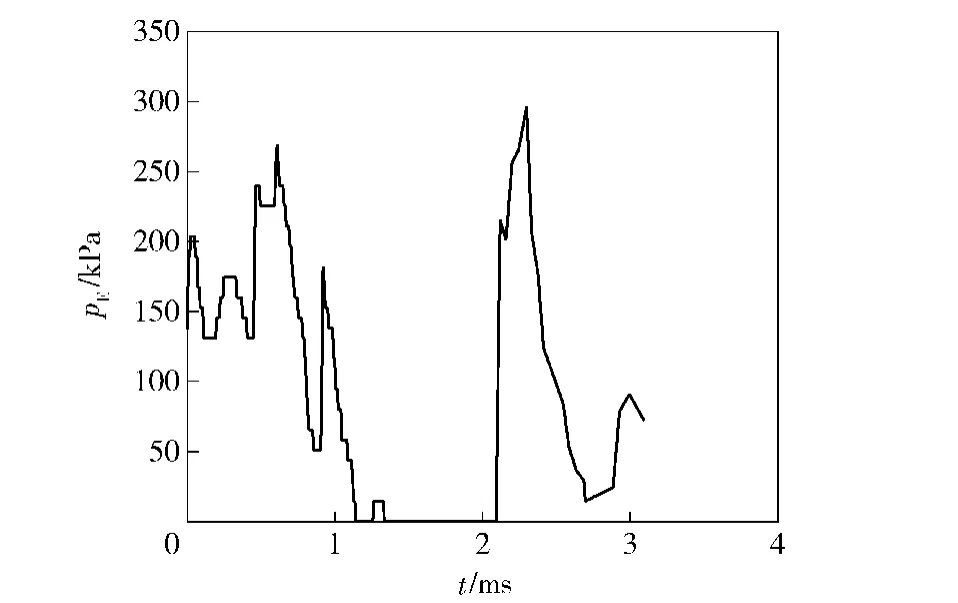
图7 复杂冲击波的实验波形Fig.7 Experimental waveforms of complex shock waves
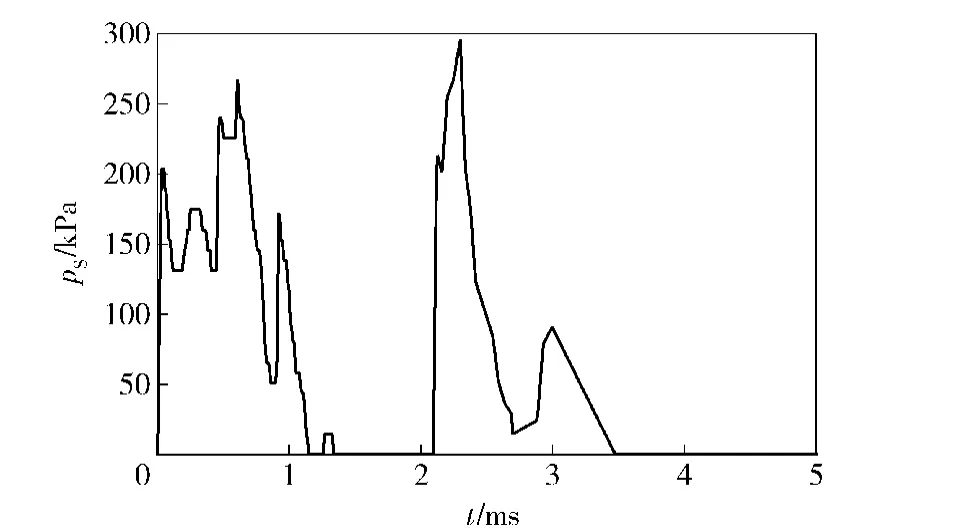
图8 数值模拟获得的复杂冲击波波形Fig.8 Simulated waveforms of complex shock waves
通过分析结果得出:模拟得到的冲击波波形与冲击波的实验波形基本一致;由于复杂冲击波的实验数据只测量到3.1 ms,所以在模拟冲击波的计算过程中,在3.1 ms后LS-DYNA软件自动将超压线性衰减到环境压力。因此,本方法可以有效地模拟复杂冲击波,模拟得到的波形与实验波形基本一致。
2.2 应用实例
利用本方法,调控超压峰值和正压作用时间,可以加载不同爆炸类型的冲击波,这对爆炸冲击波毁伤的研究有着较重要意义。图9为修正的Bowen创伤曲线[9]。
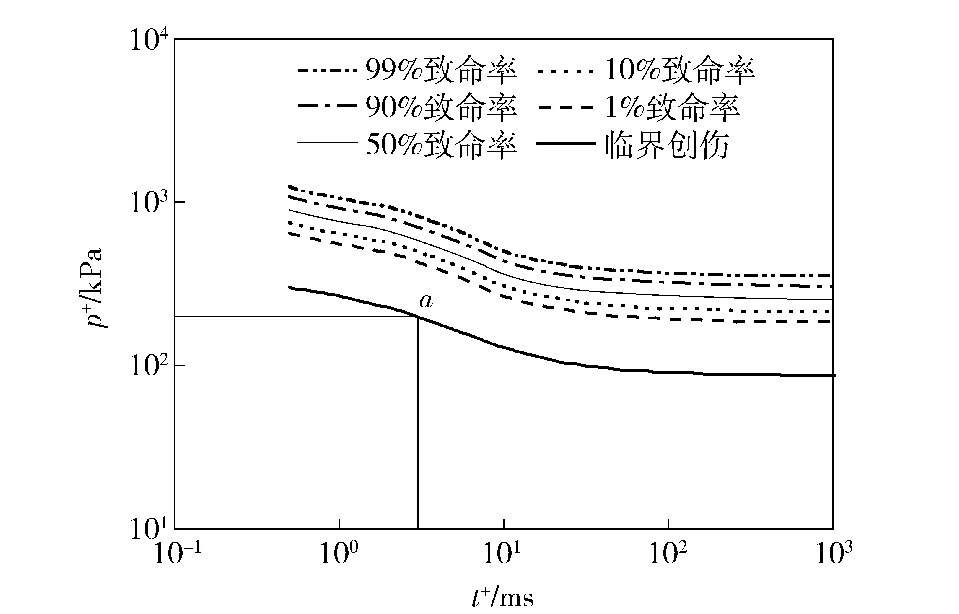
图9 修正的Bowen创伤曲线Fig.9 Modified Bowen curve
参照修正的Bowen创伤曲线,根据人体胸前入射冲击波超压峰值p+和正压作用时间t+,可获得创伤程度。图9中a点的冲击波作用于人体时,人处于临界创伤程度;a点的超压峰值p+为150 kPa,正压作用时间t+为3 ms,通过本文提供的方法,可模拟a点的冲击波波形,如图10所示。如在冲击波加载区域中加入人体模型,就可进一步研究不同类型的冲击波与人体作用的创伤机理。

图10 a点的冲击波波形Fig.8 Waveform of shock wave on Point a
以上所提供的冲击波算例,只是针对冲击波的正压相。这是由于一般所使用的压电传感器无法准确测量负压相,因为在实际操作和参数测量中,如何确定负压对创伤的影响,存在很多问题。采用这里提供的数值方法,可以很容易形成所需要的负压相,可研究其对人体目标的杀伤效应。这方面的内容在以后的研究中将给予关注。
3 结论
1)本文使用气体线性多项式的状态方程代替理想气体状态方程,既可以获得所需的冲击波,又能正确的处理边界条件,改进了文献[9-10]方法的不足。
2)给出平面冲击波方法,可以根据实验数据或Friedlander冲击波p-t曲线,通过空气线性多项式的状态方程,把p-t曲线转变为EM-t曲线,并加载到有限元程序中,可计算获得精度较高的模拟结果,误差范围在1%之内。
3)利用该方法可以有效地模拟爆炸冲击波(简单波或复杂波),为研究不同爆炸类型的冲击波创伤机理提供了有效的技术途径。
4)通过算例,给出了对应于Bowen创伤曲线的某一临界创伤条件所需要的冲击波p-t曲线,解决了现有其他数值模拟方法不能精确模拟实际冲击波的p-t曲线问题。
References)
[1] Stuhmiller J H.Biological response to blast overpressure:a summary of modeling[J].Toxicology,1997,121(33):91-103.
[2] Stuhmiller J H,Ho K,Vorst M.A model of blast overpressure injury to the lung[J].Journal of Biomechanics,1996,29(2): 227-234.
[3] Bowen I G,Fletcher E R,Richmond D R.Estimate of man's tolerance to the direct effects of air blast,DASA-2113[R]. Washington,DC:Defense Atomic Support Agency,1968.
[4] Argyros G J.Management of primary blast injury[J].Toxicology, 1997,121(1):105-115.
[5] Fernando D A,Enrique G F,Marta D M,et al.Consequence analysis by means of characteristic curves to determine the damage to humans from the detonation of explosive substances as a function of TNT equivalence[J].Journal of Loss Prevention in the Process Industries,2008,20(1):74-81.
[6] Johansson C H,Person P A.Demonic of high explosives[M]. New York:Academic Press,1970.
[7] Kinney G F.Explosive shocks in air[M].New York:The Macmillan Company,1962.
[8] LS-DYNA key word user's manual[EB].Livermore,CA:Livermore Software Technology Corporation,2003.
[9] Greer A D.Numerical modeling for the prediction of primary blast injury to the lung[D].Canada:University of Waterloo,2005.
[10] Thom C G.Soft materials under air blast loading and their effect on primary blast injury[D].Canada:,University of Waterloo, 2009.
[11] Wu C,Hao H.Modeling of simultaneous ground shock and air blast pressure on nearby structures from surface explosions[J]. International Journal of Impact Engineering,2005,31(6): 699-717.
Research on Simulating Method of Different Blast Waves
ZHOU Jie1,TAO Gang1,ZHANG Hong-wei2,PAN Bao-qing2
(1.School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.Beijing Institute of Tracking and Telecommunications Technology,Beijing 100094,China)
A method to acquire different blast waves is proposed.The geometrical models of the loading area of shock wave and air basin are established using SolidWorks,and then are divided to the structured grids by using Hypermesh.Material parameters and equation of state are assigned to the model.The curve of internal energy per unit volume and time is calculated with FORTRAN program and revised with the modified formula,then imported into the loading area of shock wave.The required shock wave is acquired by use of finite element program LS-DYNA.The proposed method can used to simulate the different blast waves with error of 1.0%.The method provides an effective route for research on blast injury.
explosion mechanics;shock wave;numerical simulation;blast injury
TJ011.1
A
1000-1093(2014)11-1846-05
10.3969/j.issn.1000-1093.2014.11.016
2013-09-22
周杰(1986—),男,博士研究生。E-mail:Beijihu1986@163.com;
陶钢(1962—),男,教授,博士生导师。E-mail:taogang@mail.njust.edu.cn
