移船架走轮与钢轨接触冲击有限元仿真分析
2014-06-27,,
,,
(1.中国人民解放军95958部队,上海 200120;2.武汉理工大学 能源与动力工程学院,武汉 430063)
移船架是船舶下水的一种重要装置,其走轮系统由数百对走轮(平衡轮、边轮)、轮轴、轴承以及轨道等结构组成[1]。在超低速运行过程中受力较为复杂,尤其在轨缝间冲击剧烈,容易引起瞬时超负荷,接触应力增大,使走轮、轮轴等结构出现变形、断裂的现象。走轮系统一旦损坏将严重影响移船架运行的安全性与平稳性。为了排除潜在的危险,提高船舶下水的安全性,必须对移船架的可靠性进行周密的计算。本文就移船架在超低速行进时的轮轨冲击状况展开讨论,分析行进速度、载荷和轨头高度差等参数对走轮在轨缝处所受冲击的影响。
1 有限元模型描述
1.1 移船架轮轨几何参数及机械性能
应用ANSYS/LS-DYNA建立钢轨与走轮的弹塑性三维有限元模型,用该模型仿真计算走轮在钢轨上低速行进时冲击钢轨轨头的过程[2-3]。此模型中钢轨采用73 kg/m重轨,走轮材料选用QT600-3号球墨铸铁。各部分几何参数见表1。
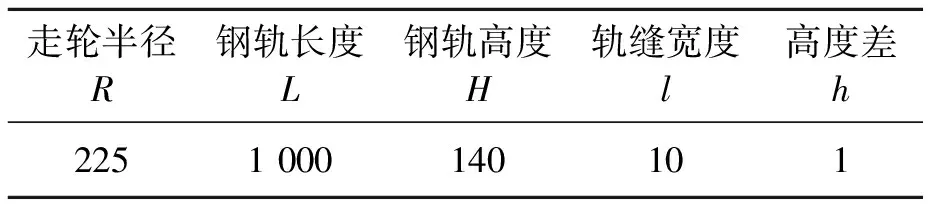
表1 走轮的几何参数 mm
走轮与钢轨力学性能如表2所列。
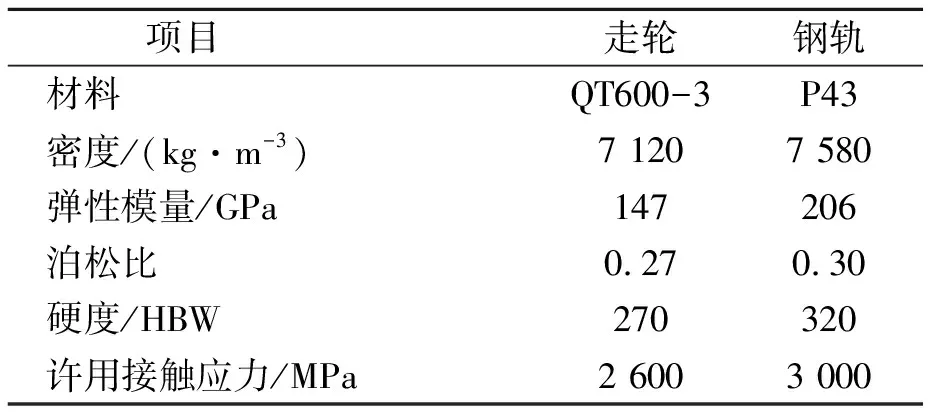
表2 轮轨材料及其力学性能
1.2 模型的建立与网格划分
考虑到分析的完整性,在仿真中采用整体建模。将其力学模型简化为二维形式,见图1。
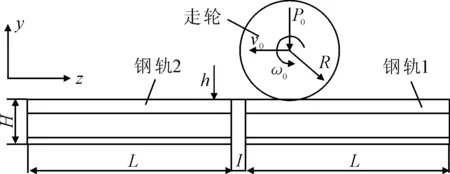
图1 轨缝冲击二维力学模型
该模型由钢轨1、钢轨2和走轮三部分组成,当走轮从钢轨1向钢轨2运动时,易在钢轨2的轨头处产生冲击。在模型中,x轴表示横向,y轴表示垂直方向,z轴表示轨道方向,即走轮的滚动方向;ω0、v0、P0、h分别表示走轮滚动角速度、走轮行进速度、荷重、钢轨错牙接头的高度差。
在仿真过程中,运用ANSYS软件的前处理功能,定义钢轨、走轮的材料属性、实常数。在显式分析过程中,用8节点3D solid164实体单元来模拟钢轨、走轮,建立模型并划分网格。走轮与钢轨接触部位网格大小细化为4 mm,其余的部分网格大小为30 mm。钢轨1有单元19 350个,钢轨2有单元18 810个,走轮单元有66 912个。有限元模型网格划分见图2。
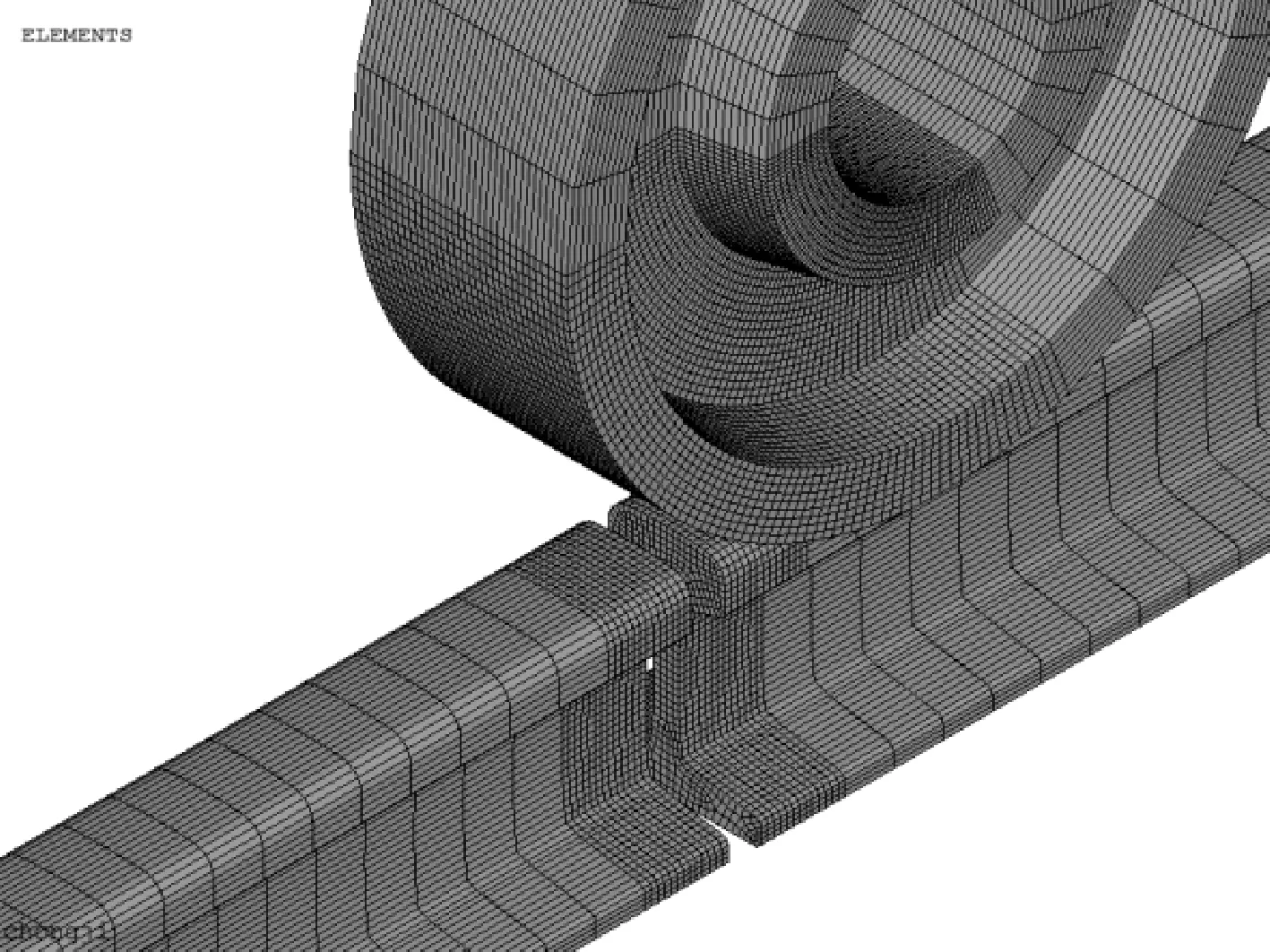
图2 轮轨模型网格划分
分别对两段钢轨和走轮创建3个part,钢轨1设为part 1,钢轨2设为part 2,走轮为part 3,part 3与part 1和part 2之间分别采用面-面接触法则,走轮与钢轨都不是刚体,且钢轨面明显小于走轮面,因此接触面为走轮面,目标面为钢轨上表面。
1.3 约束与加载
钢轨底面和两端面为全约束,走轮两侧面施加x方向约束。由于在LS-DYNA动力分析中必须考虑施加载荷随时间的变化,但这一关系无法直接通过命令设置,所以在加载前必须定义时间和载荷数组[4]。选取轮孔下表面上所有节点创建组元,定义载荷-时间历程曲线,将载荷施加到模型y方向上。走轮和钢轨三维有限元模型约束与载荷加载见图3和图4。
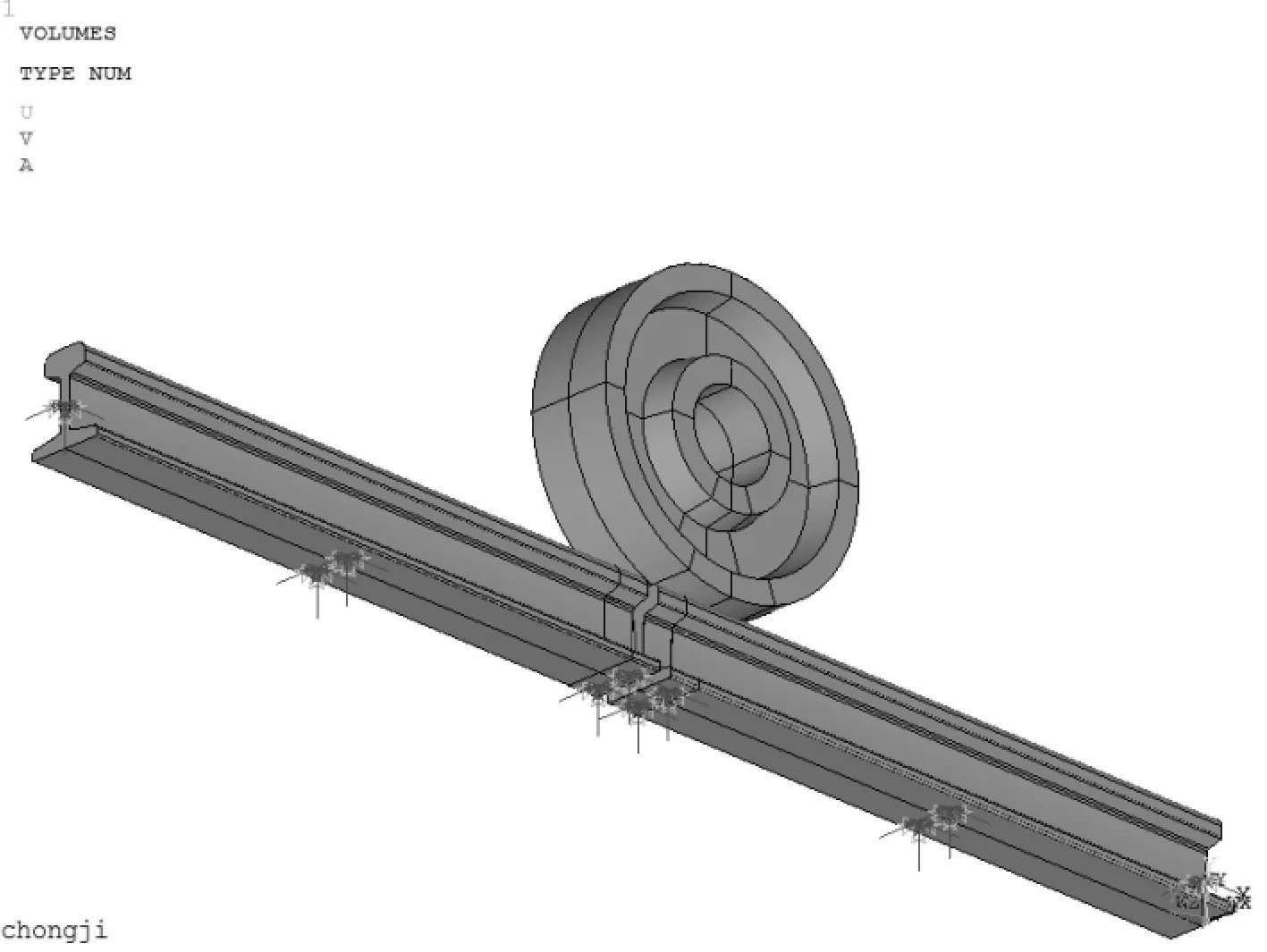
图3 面和节点的约束情况
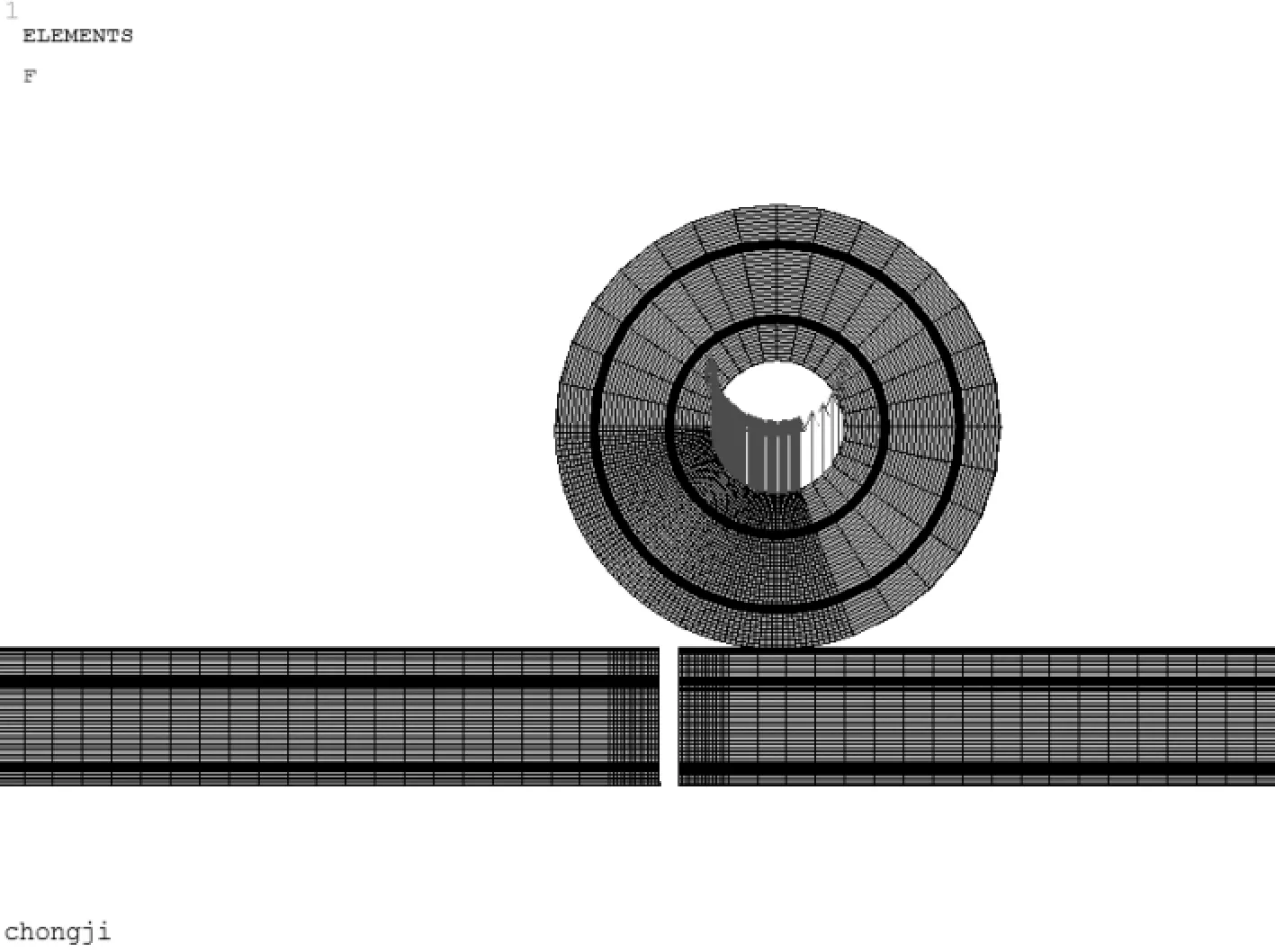
图4 载荷加载情况
2 仿真结果分析
2.1 轮轨冲击过程中的应力分析
仿真中设走轮行进速度为v0=3 m/min,走轮的载荷F=400 kN,动摩擦系数取0.2,静摩擦系数取0.3。钢轨轨头处的高度差为h=1 mm,分析时间为t=5 s,时间子步数为100,每一段分析的时间间隔为0.05 s。
计算结果如下。
2.1.1 钢轨接触应力与等效应力
钢轨yz方向接触压力随时间的变化情况见图5。yz面上的接触压力的第一个峰值出现在冲击发生之后0.3 s左右,大约是静载荷的4.9倍,为高频瞬态冲击力。冲击力的产生到消失存在于很短的时间之内,主要被钢轨轨头接触面所承受,这个冲击力是导致钢轨轨头处和走轮表面塑性变形和疲劳损伤的关键因素。在第一次峰值过后的0.2~0.3 s之后,又出现了一处比第一次稍小一点的峰值,这说明在轮轨冲击过程中钢轨可能受到了二次冲击。这种情况是钢轨的弹性势能释放而使走轮在第一次冲击过后略微的弹起,而后重新落回轨道上而引起的。
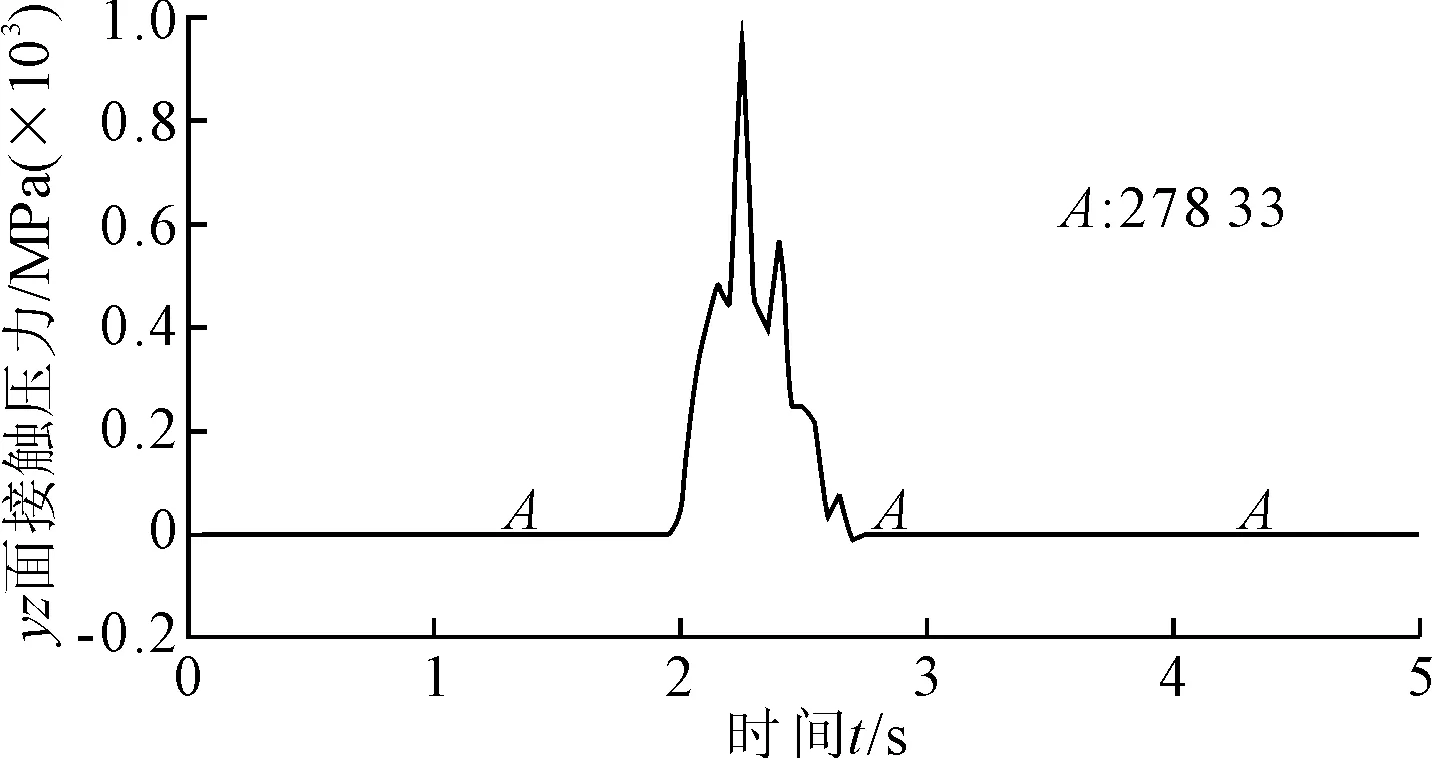
图5 yz面等效接触力随时间变化曲线

图6 轮轨冲击结果中所选单元示意
在钢轨边缘、钢轨端面和钢轨顶面选择了3个不同部位的有限元单元(见图6),来分析轮轨冲击时的应力和接触压力状况。由图7、8可见,3个测试点的von Mises等效应力、接触压力在走轮冲击钢轨之后的0.3~0.4 s内达到最大值,分别等于2 515 MPa和1 765 MPa。随着接触区域向前移动,等效应力和接触压力迅速减小。由图7可见,其边缘处的峰值最大,大约是轨面和端面峰值的2倍。
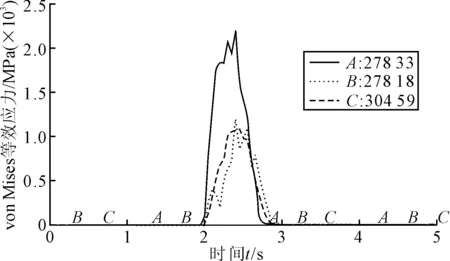
图7 3个单元von Mises等效应力随时间变化
2.1.2 走轮
轮轨开始接触产生冲击时,走轮的最大von Mises等效应力、最大接触压力在走轮冲击钢轨后0.2~0.3 s内达到最大值,分别等于1 358 MPa和2 238 MPa。随着走轮先前滚动,等效应力和接触压力迅速减小。
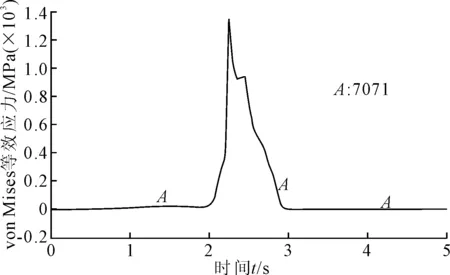
图9 走轮单元von Mises等效应力随时间变化
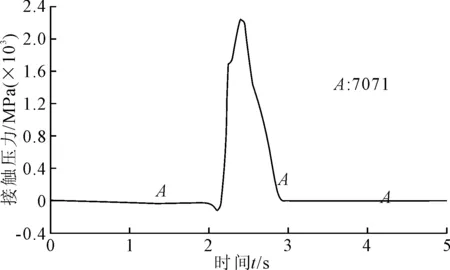
图10 走轮单元接触压力随时间变化
2.2 轮轨系统应力的影响因素
2.2.1 速度
设走轮载荷为F=200 kN,钢轨轨头处的高度差为h=1 mm,走轮行进速度为v0=3、4、5、6、7 m/min,运行时间t=5 s,时间子步数为100,每一段分析时间间隔为0.05 s。
钢轨和走轮的最大von Mises等效应力、最大接触应力都随行进速度的增加而增大,见图11、图12。这说明移船架的行进速度越快走轮与钢轨在轨缝处的安全运行风险越大。
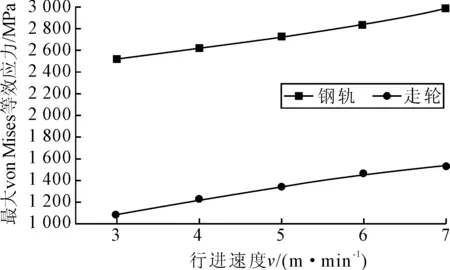
图11 轮轨最大von Mises等效应力随速度变化
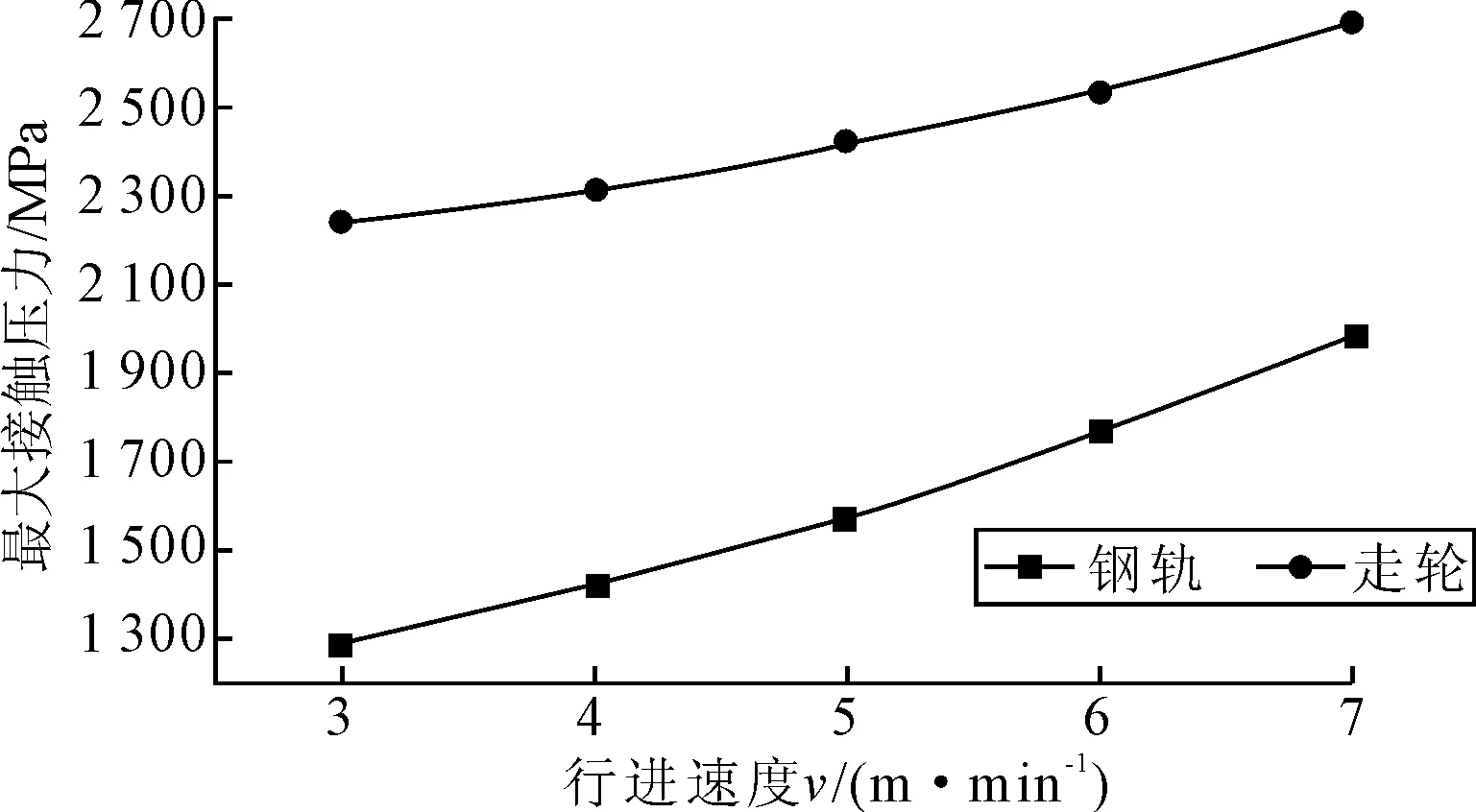
图12 轮轨最大接触应力随速度变化
计算结果表明,钢轨和走轮在冲击过程中的最大von Mises等效应力、最大接触压力有较大差异,分别在1 400 MPa和900 MPa左右。主要原因是钢轨与走轮的材料不同,弹性模量和泊松比等参数差异所致。
由于钢轨许用接触应力为3 000 MPa[5],故在最大速度7 m/min情况下可以安全使用,但此时走轮的最大接触压力为2 691 MPa,超过了其接触压力许用值。走轮在该速度下工作造成表面损伤的风险较大,因此在为了保证移船架的安全性和可靠性,其行进的最大速度不得大于6 m/min。
2.2.2 载荷
影响移船架轮轨运行过程中安全性的另一大因素是移船架的载荷。在行进速度v0=3 m/min和轨头高度差h=1 mm的条件下,载荷F分别取200、250、300、350、400 kN进行计算,重点分析钢轨和走轮在冲击过程中的最大von Mises等效应力、最大接触应力两项指标随载荷变化的趋势。见图13、14,钢轨与走轮von Mises等效应力、最大接触应力都随载荷的增大而增大,两者von Mises等效应力趋势相同,而钢轨最大接触应力增幅高于走轮,这说明载荷对钢轨轨头应力的影响大于走轮。
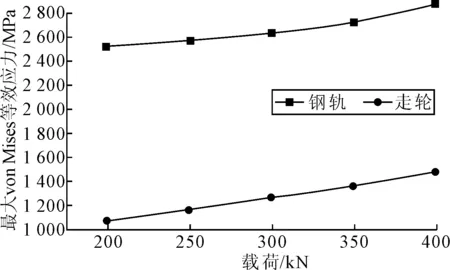
图13 轮轨最大von Mises等效应力随载重变化曲线
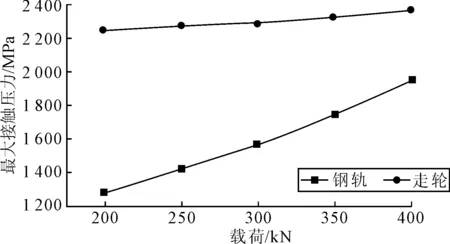
图14 轮轨最大接触应力随载重变化曲线
计算结果表明,在冲击过程中不同载荷的影响下轮轨系统的von Mises等效应力和接触应力均小于许用值,能够保证移船架的安全运行。比较两种因素对走轮系统轨缝冲击过程的影响可以看出,速度因素的影响要大于载荷的影响。因此在移船架工作过程中要严格控制行进速度。
2.2.3 轨头高度差
由于轨基的沉降作用,往往在移船架钢轨轨缝处产生一定的高度差,这种高度差对走轮在轨缝处的冲击作用存在一定的影响,在行进速度v0=3 m/min和载荷F=200 kN的条件下,分别取载荷h=0、0.5、1.0、1.5、2.0 mm进行计算。结果见图15、16。
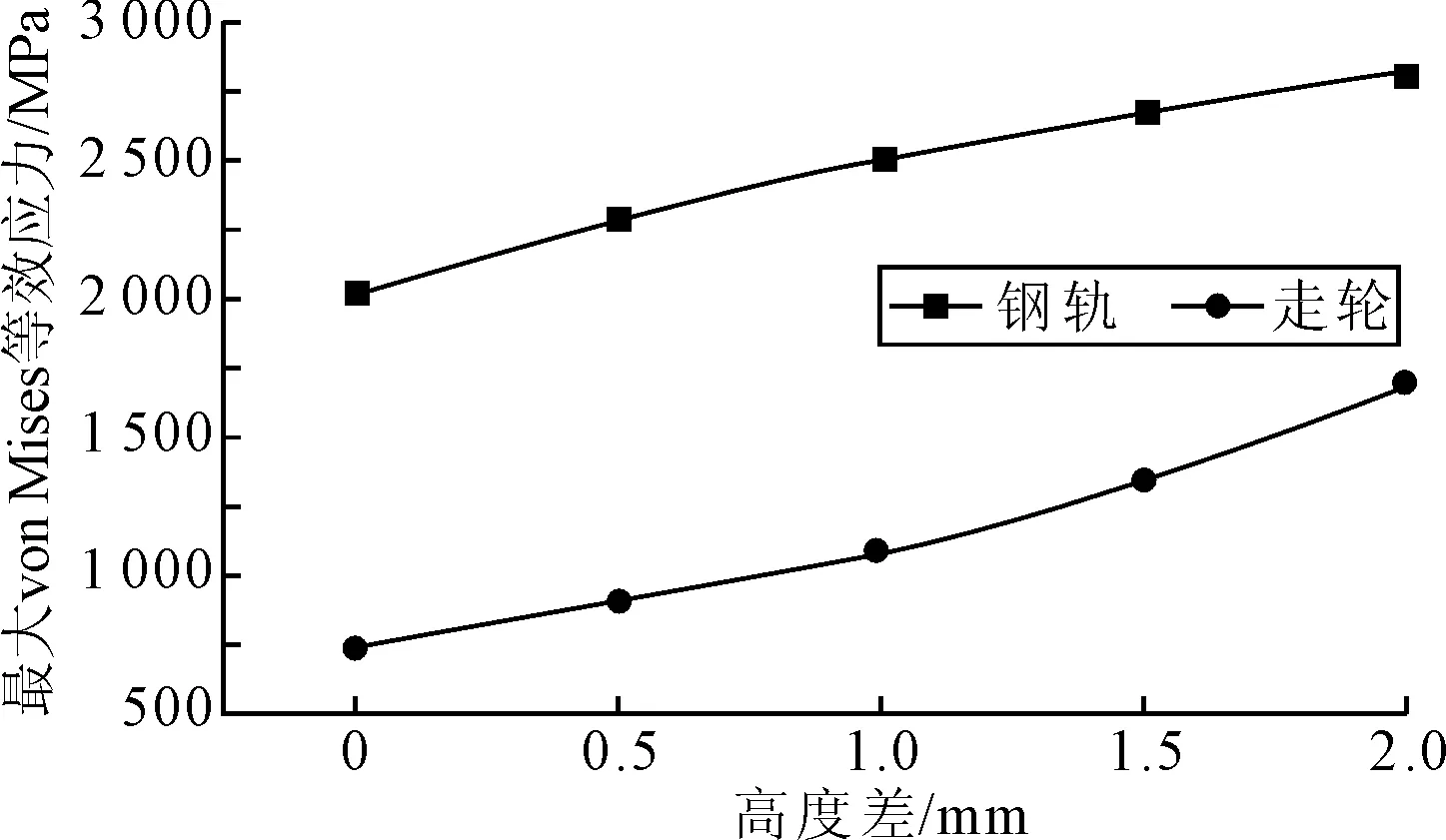
图15 轮轨最大von Mises等效应力随高度差变化曲线
可见,轨头处高度差高度越大冲击响应越明显,对钢轨和走轮的损伤越大。因此移船架钢轨应尽量保持表面平整。

图16 轮轨最大接触压力随高度差变化曲线
此外,冲击过程中因振动而出现的结构阻尼问题也是不可避免的影响因素,本文重点关注的是速度、载荷与轨头高度差的影响,结构阻尼问题不在此赘述。
3 结论
1) 当走轮冲击钢轨接头时,轮轨间的最大接触力大约是静态时的4.9倍,主要出现在钢轨接头处的接触面上。走轮在冲击钢轨后,走轮会略微弹起后回落对钢轨造成第二次冲击,容易导致走轮和钢轨接触面的损伤。
2) 轮轨的最大von Mises等效应力、最大接触应力都随行进速度、载重和轨头高度差的增加而增大。这3种参数对钢轨的影响比较明显,而对走轮的影响则相对较小。
3) 行进速度和轨头高度差对走轮系统的影响明显大于载重。在最大载重和最大轨头高度差下轮轨系统可以保证安全运行。当行进的速度为7 m/min时,接触压力大于走轮许用值,因此走轮最高行进速度应不大于6 m/min。
[1] 邹大恒. 5.7万t级散货船牵引下水工艺及实施效果
[J].船海工程,2009,38(6):6-12.
[2] 雷晓燕,管天佑.轮轨局部接触应力分析[J].华东交通大学学报,1995,12(2):20-26.
[3] 温泽峰,金学松,张卫华.钢轨轨缝接触-冲击的有限元分析[J].摩擦学学报,2003,23(3):240-244.
[4] 蔡 武.钢轨接头处轮轨接触有限元分析[D].成都:西南交通大学,2005.
[5] 周清跃,张银花,陈朝阳,等.重载铁路钢轨技术的研究[C]∥铁路重载运输货车暨工务学术研讨会.2011:56-62.
