基于SURF的特征点快速匹配算法

尧思远，王晓明，左 帅

(华北光电技术研究所，北京100015)

1 引言

匹配技术是图像处理中的一项重要内容，它将两幅相似的图像在空间中的位置作对比映射，是后续关键区域分析、相机标定等操作的基础。常见的图像匹配方法主要有两种:基于区域的匹配和基于特征的匹配。前者主要利用图像的灰度或者几何拓扑信息，通过某种相似性测度算子搜索图像空间，找出相似度最高的区域，进而得到相应的位置变化参数。该方法挖掘了图像的空间灰度分布信息，因此准确度较高，但区域搜索往往带来较大的计算量，而且对于噪声和光照的变化容忍度较差;基于特征的匹配首先寻找两幅图像中的关键特征(如关键点、线)，然后对这些关键特征做筛选、映射，得到准确的匹配。基于特征的匹配方法利用的像素数较少，可以大大减少匹配计算量，应用在对图像处理实时性要求较高的光电跟踪系统中具有明显的优势。

特征匹配的关键在于寻找一种较好的特征描述法和特征匹配算法。就点特征而言，目前常见的特征点提取方法有Harris特征、SUSAN特征、SIFT特征等［1－4］。其中，D.G.Lowe 提出的 SIFT 特征由于对光照、旋转、尺度等变换具有不变性，受到了学者的广泛关注［5］，但是SIFT特征需要进行128维的矢量特征运算，在高速视频处理系统中实时实现较为困难。Herbert Bay等提出的SURF特征在SIFT的基础上简化了图像金字塔分解的操作［6］。类似于SIFT特征，SURF特征也是一种尺度、旋转不变的特征描述方法。它对图像的卷积做近似处理，在特征点定位环节引入的积分图的概念，使求解Hessian矩阵的计算量大大降低，运算时间相比SIFT减少了3倍以上。本文结合光电跟踪系统的特点，提出一种新的基于SURF特征的改进快速近邻匹配的方法。相比于传统的匹配算法，此算法具有更高的匹配准确度。

2 光电跟踪系统中的特征点匹配

光电跟踪系统经典的目标跟踪算法主要有模板匹配、Kalman滤波等。上述方法在处理方式上虽各有不同，但是主要适用于尺度基本不变的刚体运动目标，跟踪内容主要为图像中的局部感兴趣目标区域(ROI)。对于光电图像中具有复杂畸变、尺度伸缩，方向旋转等特性的目标，采用常规的目标跟踪算法效果往往不尽如人意。基于特征点匹配的跟踪方法克服了前述跟踪方法的缺点，它通过对图像提取稳定特征点，完成前后帧特征点的匹配，并在特征点集的邻域内做局部搜索实现目标的跟踪［7－9］。如果选取的特征点具有对尺度、旋转、光照的不变性，该方法在处理复杂目标时能展现出更强的适应性。本文的研究内容即是光电图像中的SURF特征点匹配方法。光电跟踪系统中特征点匹配的主要流程为:

(1)提取相邻两帧图像的特征点;

(2)筛选感兴趣的稳定特征点，选取适当的算法对前后帧做特征点匹配，剔除误配点;

(3)在完成匹配的当前帧中采用局部搜索或仿射变换等方法定位目标。

3 SURF特征描述

3.1 快速特征点检测

SURF特征利用积分图的Hessian矩阵完成兴趣点选取和尺度变换的操作，定义点x=(x，y)处的积分图为:

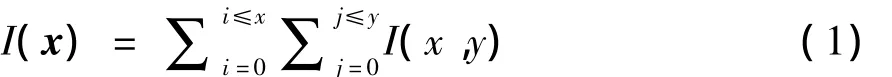
对于图像I中的某一点x，Hessian矩阵定义为:

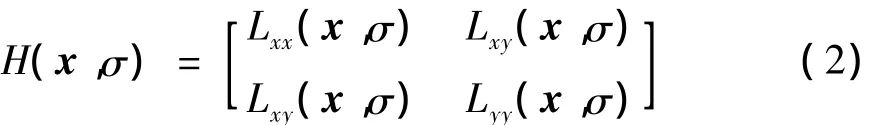
其中，Lxx(x，σ)为图像I在点x处与高斯滤波函数二阶偏导数

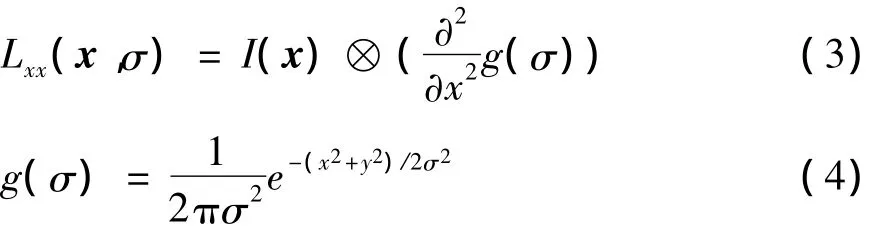
对应的，可以仿照以上两式求得Lxy(x，σ)和Lyy(x，σ)。

为简化图像与高斯滤波核卷积计算，SURF算法采用了尺度盒子滤波的方法。以9×9的盒子滤波模板为例，取尺度值s=σ =1.2，其对高斯卷积核二阶偏导的近似如图1所示。

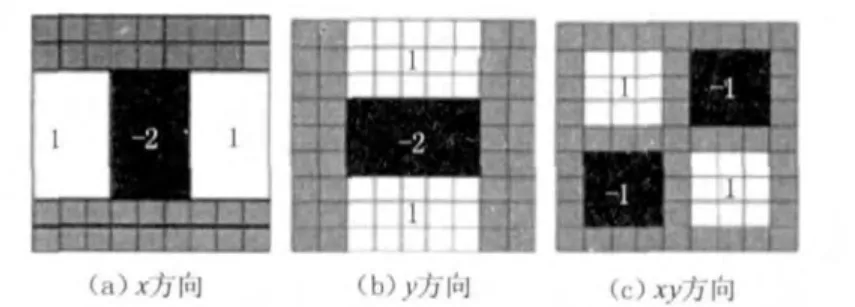
图1 高斯卷积二阶导近似

假设与上述模板卷积后得到的Hessian矩阵参数为 Dxx，Dxy，Dyy，则 Hessian 矩阵的行列式可近似为:

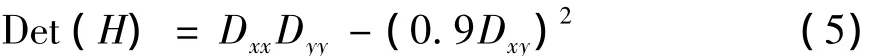
改变盒子滤波器的大小即可获得不同尺度下的卷积输出。对大小为N×N的滤波模板，对应选择的尺度s=σ=1.2×N/9，在尺度空间中取每个点的Det(H)值与该尺度相邻位置和相邻尺度周边的26个邻域比较，得到候选的局部极大值点，再对图像插值就可以计算出稳定的特征位置。

3.2 特征点主方向

为了获取图像的旋转信息，需要确定特征点的方向。以3.1节中定位出的特征点为中心，在半径为6s的圆形邻域内分别计算x和y方向的Haar小波响应。然后对卷积响应赋予高斯权重，将每π/3角度内的水平和垂直响应相加得到一个局部方向矢量，比较得出最长的矢量作为该特征点的主方向。

3.3 特征描述符生成

获得特征点主方向后，以主方向为x轴，选取20s×20s大小的区域，将其等分为4×4的子区域，在每个子区域内计算Haar小波响应，记平行于主方向和垂直于主方向的Haar小波响应为dx，dy，赋予高斯权重后统计每个子区域里响应的总和及响应绝对值之和，则每个子区域可由特征向量 V=表示。所以每个特征点就由4×4个子区域的特征向量组合而成，对特征向量做归一化处理，最终生成总计64维的特征描述符。

4 改进近邻搜索匹配

近邻欧氏距离比例法是特征点匹配中的常用方法，假设 (x1，x2…，xN)，(x1'，x2'…，xN')为一对待匹配的特征向量，由式(6)可求得特征向量的欧氏距离，比较得到候选匹配对的最近邻欧氏距离和次近邻欧氏距离之比(公式(7))，当η大于某一门限值时，表明对应的最近邻欧氏距离匹配点和次近邻欧氏距离匹配点与带匹配特征点都很接近，剔除这一配对。

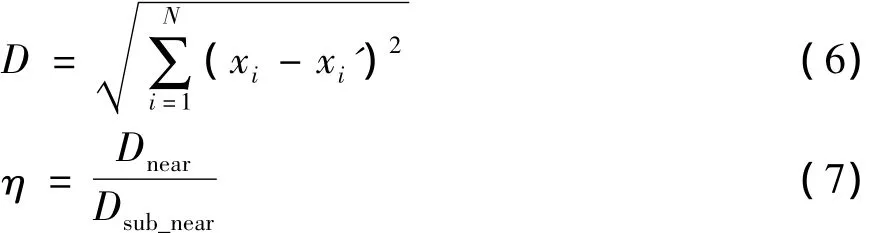
然而，近邻欧氏距离比例匹配存在明显缺陷，η门限值对匹配效果的影响很大:若选取的η较大，容易引起误匹配;若选取的η较小，虽然能够得到准确的匹配结果，但生成的匹配对很少，当图像的成像质量较差时，这一问题中尤为明显。此外，待匹配图像中往往存在相似的区域，一些相似点的SURF特征甚至比正确匹配点更接近于待匹配点。图2是用近邻欧氏距离匹配法仿真得到的结果，注意到每一花瓣周边的轮廓非常接近，不同花瓣附近SURF特征点的欧氏距离相似度有可能超过同一点的相似度，而这非常容易造成特征点误配。

图2 不同η值对匹配结果的影响

造成上述特征点误配的根本原因是待匹配的特征描述符在特定的匹配搜索策略下不具有足够高的区分度［10］。尽管SURF描述符具有丰富的64维矢量信息，而且在特征描述符生成的过程中考虑了近邻区域的Haar小波响应特性，但是SURF最终提取出的特征点只反映了单个像素信息，而仅仅依赖单个像素信息难以获得准确的匹配结果。

为了在特征点描述子中引入更多信息，T.Ojala等提出的LBP特征考虑了图像的局部纹理［11］。相应地，本文在特征匹配的过程中加入特征点近邻区域的统计信息，匹配算法的主要流程如下:

(1)计算前后帧匹配图像的SURF特征，利用式(6)和式(7)得到每个待匹配特征点F0的最近邻点与次近邻点F1和F2，F1、F2与待配点对应的欧氏距离为Dnear和Dsub_near;

(2)以待匹配的SURF特征点F0为圆心，3.2节中获取的特征点主方向对应的尺度(记为smain)为半径，建立平行于特征点主方向为Y轴，垂直于特征点主方向为X轴的正交系。分别统计圆内四个象限中灰度级大于特征点灰度的像素个数{N1，N2，N3，N4}，若统计得到的像素数为0，视该待配点为噪声点将其剔除。然后对统计结果做归一化处理，得到F0四个方向邻域的灰度分布P0={p1，p2，p3，p4}。类似地，对候选匹配点F1，F2执行相同操作，F1，F2的邻域灰度分布分别为P1={p1'，p2'，p3'，p4'}和 P2={p1″，p2″，p3″，p4″};

(3)依据最近邻欧氏距离比率法进行粗匹配，在式(7)中将起始阈值设为η1，初步选出区分度较强的特征点;

(4)在确定上一帧图像中满足步骤(3)中粗匹配条件的特征点后，计算当前匹配帧中与之对应最近邻点邻域灰度分布的Pearson相关系数。Pearson相关系数的表达式为:

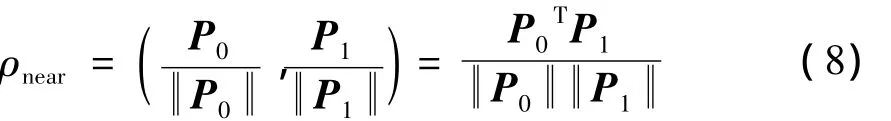
用同样的方法计算出次近邻点灰度分布相关系数ρsub_near;

(5)候选特征点再匹配。对符合粗匹配要求的特征点求取近邻灰度分布相关系数比若η'大于阈值η2，则确定此时得到的最近邻点为正确匹配点，否则，剔除此对匹配。

上述算法的关键在于匹配过程中引入了二次匹配。最近邻比例法首先用于特征点的粗匹配，初步挑选出区分度较好的待配点，然后统计特征点在其对应尺度下的四邻域灰度分布信息，并引入Pearson相关系数对待配点做进一步挑选，得到最终的匹配对。

5 实验结果与结论

5.1 实验结果

根据以上论述，将算法应用于采集的光电跟踪系统图像中。以车牌跟踪为例，图像的尺寸为640×480，实验平台为 Intel i5－2400 3.1GHz四核处理器、4G内存，分别用最近邻欧氏距离比例法和本文提出的算法对已提取SURF特征的两帧图像进行匹配，得到的结果如图3所示。

图3 车牌匹配效果对比

表1为近邻比例法与本文算法对提取的车牌目标特征匹配的性能比较，由表中数据可以看出，本文算法的匹配成功率达到95.45%，相比近邻比例法在准确度上有较大幅度提升;此外，由于实验中并未对提出的算法做并行优化处理，因此在计算时间方面相比近邻比例法有明显提升，但17.87 ms的处理耗时依然能满足一般光电系统的实时性要求。

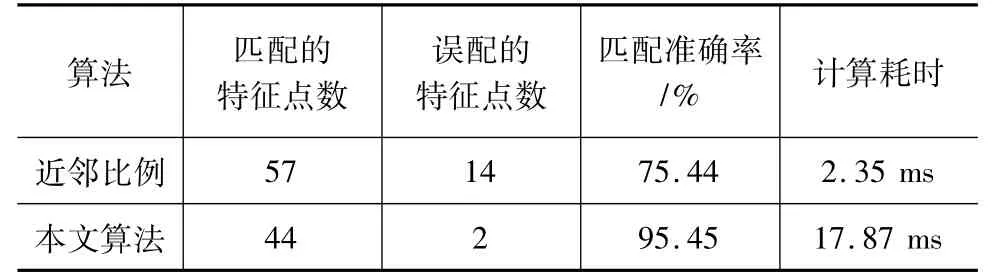
表1 匹配性能比较

5.2 结论与展望

实验表明本特征点匹配算法具有较好的匹配性能。SURF特征提取算法首先被用于提取光电图像序列中鲁棒的特征点，接下来在点匹配的不同阶段采用了不同策略:将误配率较高的欧氏距离比率法作为第一级粗匹配，然后将特征点周边的灰度信息引入匹配准则中，从而大大提高了匹配准确率。值得一提的是，该算法虽然利用了图像的灰度信息，但挖掘并不充分，而且在计算时间方面还有待优化。在后期的改进工作中，有必要重点考虑特征点周边局部纹理以及聚类分析方法在本研究中的应用。

［1］ Harris C，Stephens MJ.A combined corner and edge detector［C］.Processing of Fourth alvey Vision Conference，1988:147－151.

［2］ L Jing，N Allinson.A comprehensive review of current local features for computer vision［J］.Neurocomputing，2008(2):1－17.

［3］ Z Zhen，H Wang，E Teoh.Analysis of gray level corner detection［J］.Pattern Recognition Letters，1999，20(2):149－162.

［4］ S M Smith，J M Brady.SUSAN － a new approach to low level image processing［J］.International Journal of Computer Vision，1997，23(1):43 －78.

［5］ Lowe D G.Dinstinctive image features from scale－invariant keypoints［J］.International Journal of Computer Vision，2004，60(2):90 －110.

［6］ Bay H，Tuytelaars T，Van Gool L.SURF:speeded up robust features［C］.European Conference on Computer Vision，2006:1:404 －417.

［7］ Song Lin，Chen Yongmei，Song Chunhua，et al.Image matching method based on weighted shape context［J］.Laser＆ Infrared，2013，43(5):826 －830.(in Chinese)宋琳，程咏梅，宋春华，等.基于加权形状上下文的图匹配［J］.激光与红外，2013，43(5):826 －830.

［8］ Yang Dongdong，Chang Danhua，Han Xia.Improvement and realization of the moving object detection and tracking［J］.Laser and Infrared，2010，40(2):205 －209.(in Chinese)杨冬冬，常丹华，韩夏.运动目标检测与跟踪算法的改进与实现［J］.激光与红外，2010，40(2):205 －209.

［9］ La Tuan Anh，Jae － Bok Song.Object tracking and visual servoing using features computed from local feature descriptor［C］.International Conference on Control Automation and Systems，2010:1044 －1048.

［10］ Bian Houqin，Su Jianbo.Feature correspondence algorithm based on scene － independent constraint［J］.Journal of Image and Graphics，2006，11(3):342 －348.(in Chinese)边后琴，苏剑波.场景无关约束下的特征匹配方法［J］.中国图像图形学报，2006，11(3):342 －348.

［11］ Timo Ojala，Matti Pietikainen，Topi Maenpaa.Multiresolution Gray－scale and rotation invariant texture classification with local binary patterns［J］.IEEE Transactions on Pattern Recognition and Machine Intelligence，2002，24:971 －987.