一种改进的边缘细化方法

许宏科，秦严严，潘 勇

(长安大学电子与控制工程学院，陕西西安710064)

一种改进的边缘细化方法

许宏科，秦严严，潘 勇

(长安大学电子与控制工程学院，陕西西安710064)

针对Sobel算子检测出的图像边缘较粗且检测效果受噪声影响大的问题，提出了一种结合自适应平滑滤波并改进原细化算法的方法来抑制噪声并细化边缘。使用新的自适应平滑滤波梯度模板对原始图像滤波，在平滑噪声的过程中锐化图像边缘;在Sobel算子检测出边缘后使用改进的细化算法剔除伪边缘点。试验比较表明:在迭代次数相同的情况下，新的自适应平滑滤波模板比原梯度模板总体效果更好;改进的边缘细化算法在保证与原算法运算时间相当的条件下，保留了更多的边缘细节信息，细化结果更加准确。

图像处理;边缘细化;自适应平滑;Sobel算子;边缘检测

1 引言

图像边缘是图像的一种重要特征，图像边缘的确定和提取对于图像分析是非常重要的，长期以来是图像处理中的研究热点，人们期望找到一种抗噪性好、不漏检、不误检且快速的方法[1]。经典的算法中常用梯度算子[2]，如 Roberts算子、Prewitt算子和 Sobel算子[3－6]，其中 Sobel算子检测效果比较好，Sobel算子优点在于方法简单，处理速度快，检测出的边缘平滑、连续。但其缺点是检测出的边缘较粗且对噪声较敏感[6－7]。

噪声对图像后续处理产生着很大影响，在边缘检测与细化之前，需要做好滤波处理。常用图像滤波方法在抑制噪声的同时，模糊了图像边缘[8]，对后续边缘检测与细化造成了消极影响。文献[9]提出一种基于梯度信息的自适应平滑滤波方法，其基本思想是用一种小的平均加权模板与原始图像进行迭代卷积，每次迭代时自适应地改变各像素加权系数。在区域平滑的过程中，较好地抑制了噪声，同时锐化了边缘。但其缺点是使用的梯度模板过于简单，没有充分利用8邻域像素点信息，针对这一缺陷，本文使用一种新的梯度模板代替原梯度模板，新梯度模板考虑了8邻域内所有像素点信息，在迭代次数相同的情况下，比原梯度模板滤波总体效果更优。

二值边缘图像细化算法的研究一直以来都受到学者们的关注，二值边缘图像只包含是否归属于边缘点的信息[10]，真为1，假为0。经典细化算法有Zhang[11]，Hall[12]，Holt[13]，Park[14]，Prewer[15]等，这些算法之中细化效果较好且速度较快的是文献[12]和[13]中提出的HSCP算法。但HSCP算法保留了孤立边缘点，且其采用两层循环遍历构成一次迭代，运算量较大[16]。文献[16]对它进行了改进:增加边缘孤立点判断条件;采用一层循环遍历构成一次迭代，减少了运算量。但运算量的减少是以增加边缘点漏检量为代价，过多地剔除了边缘细节。本文在HSCP算法思想基础之上，针对文献[16]中的缺陷，仍然使用一层循环搜索作为一次迭代过程，通过增加伪边缘点的判断条件，在细化速度与文献[16]相当的前提下，有效地克服了文献[16]对边缘细节漏检这一问题，保留了更多的边缘细节。文献[16]中边缘细化算法选用为本文试验对比算法。

2 自适应平滑滤波

自适应平滑滤波器是利用一种小的平均加权模板与图像进行迭代卷积，该模板的权系数是由对应点的信号的连续性，即作为像素点梯度的函数来决定[17]。这种自适应平滑滤波的迭代运算在抑制噪声的同时，使图像的边缘锐化，此时再进行边缘检测，可以得到很高的边缘定位精度。自适应平滑滤波具体原理详见文献[17]，其一次迭代的计算步骤如下:

Step1:计算梯度分量 Gx(x，y)，Gy(x，y)

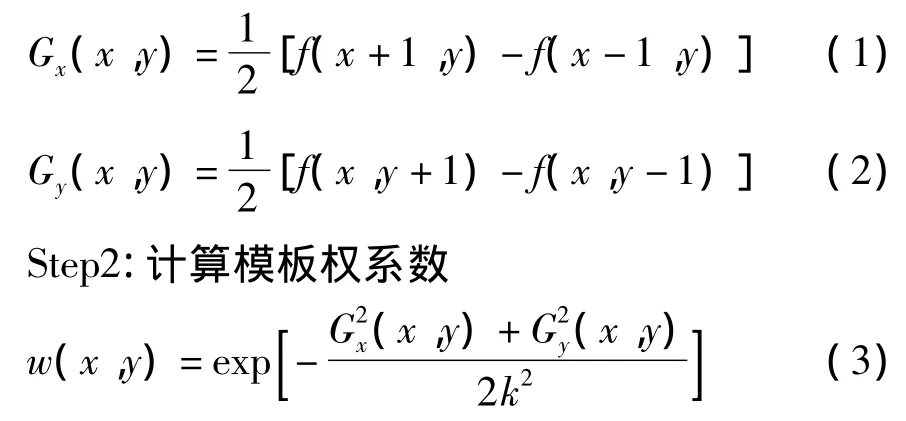
Step3:对图像f(n)(x，y)进行加权平均

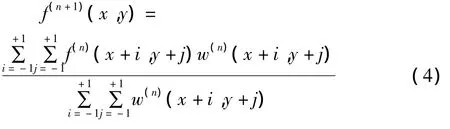
其中，式(3)中的参数k为计算之前需要设定的参数，它决定了具有多大幅值的突变边缘将得到保存，本文试验中设定k=10;f(n)(x，y)为第n次迭代后的图像，假定迭代次数 N，则 n=0，1，…，N－1。最后输出迭代N次之后的结果图像f(N)(x，y)。

由梯度计算式(1)和(2)可以看到，梯度Gx(x，y)，Gy(x，y)可以由两个对应的梯度模板h和hT(模板h的转置)与图像f(x，y)进行滤波实现。模板h(hT只需将h转置即可)如图1(a)所示。

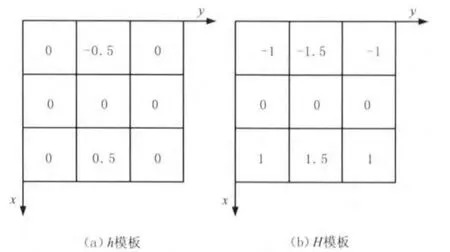
图1 自适应品平滑梯度模板

从图1(a)中可以看出，自适应平滑滤波算法在计算梯度时，仅仅考虑了中心点像素x轴(或y轴)方向上相邻两像素信息，中心点8邻域的其余像素信息均未被利用，这使得达到某一理想滤波效果时需要较多的迭代次数。为了充分利用中心点8邻域像素信息，并减少迭代次数，本文给出一种新的梯度模板H(通过转置得到HT)，如图1(b)所示。

由图1(b)可以看到，新梯度模板充分考虑了中心点8邻域的像素信息，模板权系数更加准确，抗噪性能更好。迭代相同的次数，与原梯度模板相比，用新梯度模板H滤波的总体效果有所提高，在去噪的同时能有效地锐化边缘。使得后续的边缘检测与细化更准确。

3 Sobel算子边缘检测

在对原图像进行N次自适应滤波迭代后，得到滤波后图像f(N)(x，y)。此时再用Sobel算子进行边缘检测将大大降低了噪声影响，而且锐化了图像边缘，使得Sobel算子检测出的边缘更准确，更有利于后续细化工作。

Sobel算子是基于一阶微分方法，首先进行邻域加权平均，然后进行一阶微分处理，最后二值化处理，检测出边缘点。Sobel算子使用的梯度模板如图2所示。

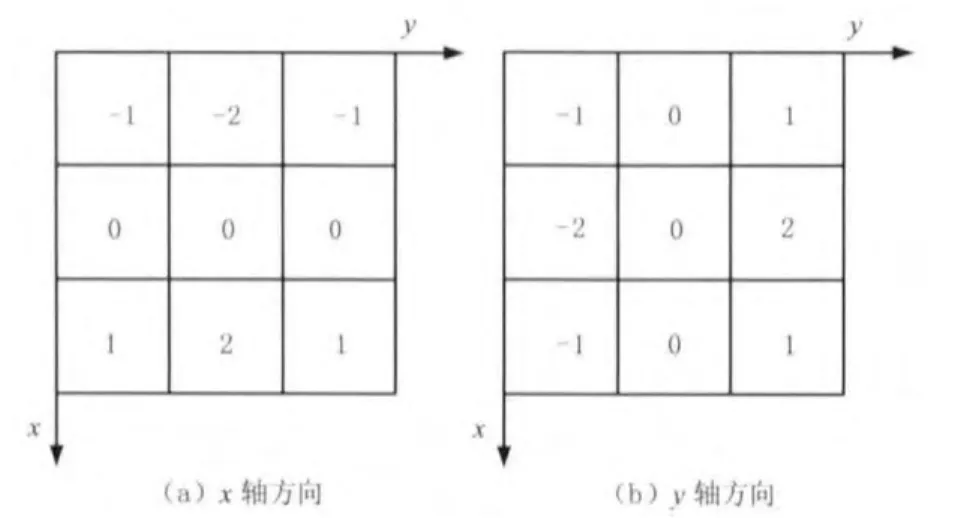
图2 Sobel算子梯度模板

设g(x，y)为上述自适应平滑滤波后的图像，则g(x，y)的梯度分量gx和gy可用图2中的两个模板通过滤波整个图像来实现，如式(5)和(6)所示。

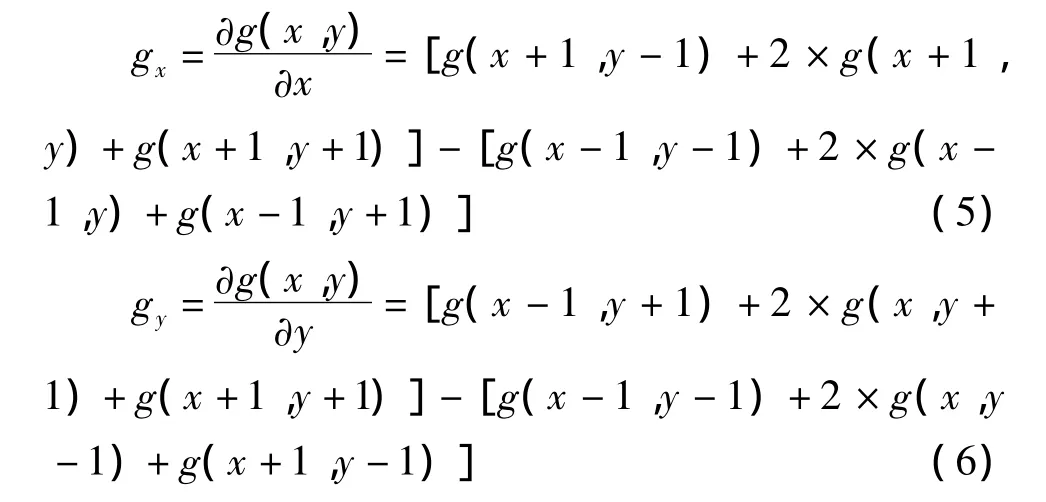
然后通过式(7)求得g(x，y)的梯度幅值M(x，y):

最后通过设定阈值T，对M(x，y)二值化处理，认为M(x，y)中像素值大于等于T的是边缘点，像素值置1，否则为0，完成对图像 g(x，y)的边缘检测。总结Sobel算子边缘检测的步骤[18]:

(1)分别将2个方向模板沿着图像从一个像素移动到另一个像素，并将像素的中心与图像中的某个像素重合;

(2)将模板内的系数与图像上相对应的像素值相乘，并将所有相乘的值相加，计算梯度分量;

(3)利用两个梯度分量的值，计算梯度幅值;

(4)选取合适的阈值T，若梯度幅值大于等于T，则认为该像素点为图像边缘点。

用Sobel算子检测的边缘较粗，需要对其细化，以便得到更精确的边缘信息。

4 边缘细化

图像细化就是从原来的图像中去掉一些点，但仍要保持目标区域的原来形状[19]。二值边缘图像细化即是判断原边缘上每一像素点是否应被剔除，以此来一层层剥离原边缘最外层的伪边缘。

4.1 HSCP边缘细化算法

首先给出图像中像素点8连通域示意图，如图3所示。则HSCP算法可简述如下[10]:

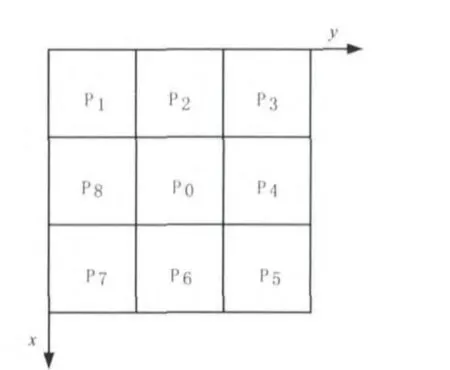
图3 8连通域示意图

Step1:针对所有的边缘点P0，若满足如下条件，则判断其为待剔除点。

(1)其8连通域中的边缘点数E(P0)满足:2≤E(P0)≤6;

(2)P0的8连通域包含且只包含一个4连通边缘点。

Step2:遍历所有的待剔除点，若满足如下条件之一，则保留，否则删除。

(1)P2，P6为边缘点，但P4为待剔除点;

(2)P4，P8为边缘点，但P6为待剔除点;

(3)P4，P5，P6均为待剔除点。

以上两步操作构成一次迭代，不难发现，在每次迭代中需两次循环遍历，首先需遍历全部边缘点，判断是否为待剔除点;然后再次遍历全部待剔除点，再次判断这些点是否确实可剔除，目的是防止过多地剔除边缘细节，保持原有边缘的连续性。此算法计算量较大。

4.2 试验对比算法

针对HSCP算法思想步骤，文献[16]指出其两个缺陷:

(1)保留了孤立的边缘点。因为孤立点8邻域内非零点的个数为0，即E(P0)=0，而待剔除点必须满足2≤E(P0)≤6，所以孤立点未被剔除。

(2)运算量较大。采用两层循环构成一次迭代，尽管每次迭代对象不尽相同，算法开销依然较大。

文献[16]的算法步骤如下:

(1)如果E(P0)=0，则剔除该边缘点。

(2)如果2≤E(P0)≤6，且 S(P0)=1，则标记为待剔除点，一次遍历完后剔除。

其中，S(P0)是以 P1，P2，...，P8为序列的点，其像素值从0到1变化的次数。以上两步骤构成一次遍历。第二步需反复迭代，直至没有点再满足标记条件为止。

文献[16]使用一层循环遍历作为一次迭代，大大降低了运算量，但其在标记待剔除点后，没有进一步判断待剔除点对原边缘连续性的影响，而是一概剔除，这样就过多的剔除了原边缘细节。本文依据HSCP算法思想，对文献[16]作出改进，在保持运算量较小的前提下，克服文献[16]对原边缘点漏检这一问题，保留更多的边缘细节。

4.3 本文细化算法

虽然原图像有些边缘点满足文献[16]中2≤E(P0)≤6，且S(P0)=1的条件，被标记为待剔除边缘点，但仍需要进一步判断剔除这些边缘点是否影响原边缘连续性，否则会过多地剔除边缘细节。例如，当边缘点P0在8邻域某一方向上宽度为1，且其满足2≤E(P0)≤6，S(P0)=1的条件时，将P0剔除的后果是使原边缘从P0处断裂，破坏了原边缘的连续性。极端情况下，经过多次迭代，边缘在细化的过程中，原边缘在多处断裂，甚至支离破碎。

本文在标记出待剔除边缘点P0后，考虑其8邻域(图3)水平、垂直、斜对角四个方向上的像素信息，作为判断是否确实可将其剔除的条件。判断条件如下:

(1)P4=0且P8=0;

(2)P2=0且P6=0;

(3)P1=0且P5=0;

(4)P3=0且 P7=0。

若以上四个条件中有一个满足时，则保留待剔除边缘点P0;只有当四个条件都不满足时，才可将P0剔除。

考虑改进后细化算法要和原算法运算量相当，这样提高细化效果才有意义，故本文仍然采用一层循环做为一次迭代过程。Sobel算子边缘检测后，针对所有边缘点P0，改进的细化算法步骤如下:

Step1:若E(P0)=0，则直接剔除该边缘点。

Step2:若满足如下条件，则标记P0为待剔除边缘点。

(1)2≤E(P0)≤6;

(2)S(P0)=1;

(3)P4+P8≠0，P2+P6≠0，P1+P5≠0 且 P3+P7≠0;

Step3:一次循环遍历后，将标记为待剔除点像素置0，将其剔除。

以上三步构成一次遍历，Step2和Step3需要迭代，直到没有满足标记的条件为止。本文的改进算法较文献[16]算法在细化效果上有明显提高，而且运算量并没有显著增加，具体分析见5.2小节。

5 试验结果及分析

5.1 自适应平滑滤波试验分析

首先给Lena图像添加均值为0、方差为0.04的均匀分布的随机噪声，作为试验对象，然后分别对其进行高斯滤波、自适应平滑滤波和使用改进模板的自适应平滑滤波，得到不同的滤波效果。并进一步使用高斯拉普拉斯(LoG)算子[20]，对三种滤波后的图像进行边缘检测，以验证这三种滤波对后续边缘检测的影响，如图4所示。

图4 滤波效果对比图

图4中，(d)、(f)、(h)分别是(c)、(e)、(g)进行LoG边缘检测效果图;(c)是(b)经过连续5次的滤波效果;(e)的自适应滤波迭代次数取5，而(g)的自适应滤波迭代次数取3。

由图4(c)和(e)可以看出自适应平滑滤波要优于高斯滤波，可以从(d)和(f)的比较看出自适应平滑滤波对后续边缘检测的积极作用;比较(e)和(g)以及(f)和(h)，可以发现使用新模板进行自适应平滑滤波的3次迭代效果和原模板5次迭代效果相当，在达到滤波效果相同的情况下，减少了迭代次数，运算量大大减少。

5.2 边缘细化试验对比分析

在Sobel算子初步检测出边缘后，对其分别使用本文改进算法和文献[16]细化算法进行边缘细化试验，分析两种算法的细化效果与算法运算时间，验证了本文改进算法的准确性、快速性、优越性。在下面的分析中，将本文改进算法简记为 A1，文献[16]细化算法简记为A2。

5.2.1 细化效果对比

图5显示了Lena图像在Sobel算子检测边缘后，分别用算法 A1和 A2进行细化的效果对比情况。

图5 A1、A2细化效果对比

由图5中(b)和(c)可以看出，A1算法可以有效地细化原边缘，保持了原边缘骨架完整性，体现了准确性;由(c)和(d)可以看出，A1算法细化效果与A2算法相比较，A1算法保留了更多边缘细节，图像边缘连续性更强，充分说明了本文改进算法比原算法在细化效果上的优越性。

5.2.2 细化运算量对比

从所做试验中选取10幅标准512×512图像，每幅图像分别用A1算法和A2算法做细化试验，统计细化运算时间，如表1所示。

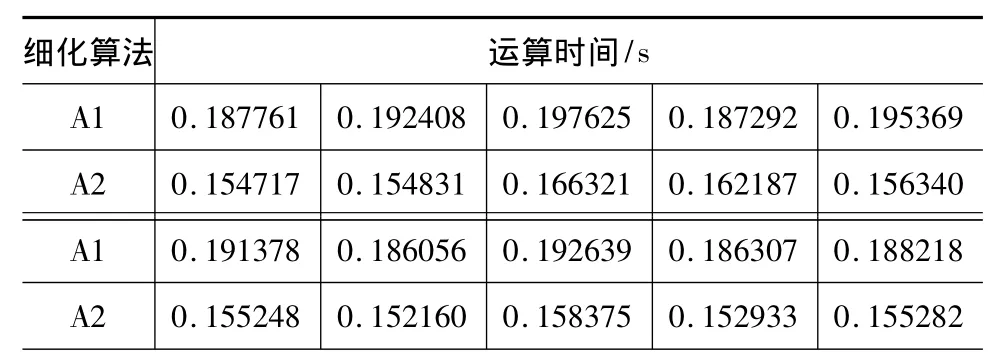
表1 细化运算时间

从表1中可以粗略地看出A1算法运算时间比A2运算时间稍长，但差别较小。为了更直观地比较两种算法运算时间，以试验次数为横坐标，以对应运算时间为纵坐标，画出两种算法的运算时间曲线，如图6所示。

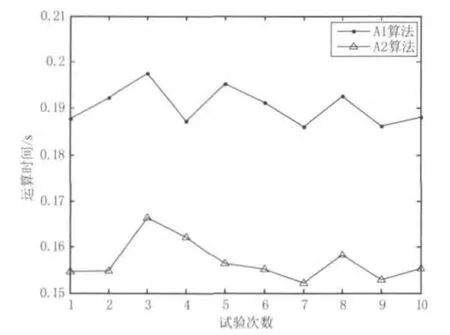
图6 运算时间曲线对比图

由表1计算得，A1算法运算时间平均值为0.1905s，A2算法运算时间平均值为0.1568s，差值仅为0.0337s，相差很小。且从图6中也可以看出两种算法运算时间曲线高度均在0.1s范围内，充分表明了本文改进算法运算时间和原算法相当。

5 结论

本文提出一种结合自适应滤波的改进细化算法对Sobel算子检测出的边缘进行细化，并将改进算法和原算法做了对比试验。得出以下结论:①自适应平滑滤波可以在抑制噪声的过程中锐化边缘，对后续边缘检测起积极作用;②使用新梯度模板自适应滤波比用原梯度模板迭代次数更少，总体效果更好;③本文改进细化算法相比于原细化算法，可以保留更多边缘细节，保持边缘连续性;④用Matlab对标准512×512图像进行边缘细化仿真，两种细化算法平均运算时间仅相差约0.0337s，表明本文改进算法运算时间与原算法相当。

[1]Zhang Yujin.Image engineering[M].Beijing:Tsinghua University Press，1999.(in Chinese)章毓晋.图像工程[M].北京:清华大学出版社，1999.

[2]Zhang Jiande，Shao Dinghong.Thread edge detection based on sobel thinning algorithm[J].Mechinery ＆ E-lectronics，2007，05:77 －78.(in Chinese)张建德，邵定宏.基于Sobel细化算法的螺纹边缘检测[J].机械与电子，2007，05:77 －78.

[3]He Jiandong，Geng Nan，Zhang Yikuan，et al.Digital im-age processing[M].Xi'an:Xi'an Electronic Sience ＆Technology University Press，2003:95 －97.(in Chinese)何建东，耿楠，张义宽，等.数字图像处理[M].西安:西安电子科技大学出版社，2003:95－97.

[4]Health A，Sarkar S，Sanocki T，et al.Camparison of edge detectors:A methodology and initial syudy[J].Computer Vision and Image Understanding，1998，69(1):38 －54.

[5]Rosenfel A.Computer vision:a source of models for biological visual process[J].IEEE Transactions on Biomedical Engineering，1989，36(1):83 －94.

[6]Sobel I.Neighbourhood coding of binary images fast contour following and general array binary processing[J].Computer Graphics and Image Processing.1978，(8):127－135.

[7]Canny J.A computational approach to edge detection[J].IEEE Trans Pattern Analysis Mach Intell，1986，8(6):679－698.

[8]Liu Guofeng，Guo Wenming.Application of improved arithmetic of median filtering denoising[J].Computer Engineering and Applications，2010，10:187 －189.(in Chinese)刘国宏，郭文明.改进的中值滤波去噪算法应用分析[J].计算机工程与应用，2010，10:187 －189.

[9]Jing Xiaojun，Li Jianfeng，Xiong Yuqing.An adaptive smooth filter algorithms of still images[J].Journal on Communications，2002，10:6 －14.(in Chinese)景晓军，李剑峰，熊玉庆.静止图像的一种自适应平滑滤波算法[J].通信学报，2002，10:6 －14.

[10]Tan Yusong，Zhou Xingming.Connectivity preserved edge thinning algorithm[J].Journal of National University of Defense Technology，2004，4:51 －56.(in Chinese)谭郁松，周兴铭.保持连通的边缘细化算法[J].国防科技大学学报，2004，4:51 －56.

[11]Zhang T Y，Suen C Y.A fast parallel algorithm for thinning digital patterns[J].Communication of the ACM.March，1984，27(3):236 －239.

[12]Hall R W.Fastparallelthinning algorithms:parallel speed and connective preservation[J].Communication of the ACM.Jan，1989，32(1):124 －131.

[13]Holt C M.An improved parallel thinning algorithm[J].Communication oftheACM.Feb，1987，30(2):156－160.

[14]Park Jung Me.A new gray level edge thinning method[R].The University of Alabama，2000.

[15]Prewer D，Kiteben L.A fast table method for edge thinning and linking[R].Tech.Report，WP1999/9，The University of Melbourne，1999.

[16]Kang Mu，Xu Qinggong，Wang Baoshu.A roberts'adaptive edge detection method[J].Journal of Xi'an Jiaotong University，2008，10:1240 －1244.(in Chinese)康牧，许庆功，王宝树.一种Roberts自适应边缘检测方法[J].西安交通大学学报，2008，10:1240 －1244.

[17]Zheng Nanning.Computer vision and pattern recognition[M].Beijing:National Defense Industry Press，1998:69 －79.(in Chinese)郑南宁.计算机视觉与模式识别[M].北京:国防工业出版社，1998:69－79.

[18]Liu Cai.An improved sobel algorithm for edge detection[J].Journal of Guizhou University of Technology:Natural Science Edition，2004，5:77 －79.(in Chinese)刘彩.一种改进的Sobel图像边缘检测算法[J].贵州工业大学学报:自然科学版，2004，5:77－79.

[19]Lü Junbai.An efficient thinning algorithm for binary images[J].Computer Engineering，2003，18:147 － 148.(in Chinese)吕俊白.一种有效的二值图像细化算法[J].计算机工程，2003，18:147 －148.

[20]Gonzalez R C.Digital image processing using MATLAB[M].Beijing:Publishing House of Electronics Industry，2005:290 －292.(in Chinese)冈萨雷斯.数字图像处理(MATLAB版)[M].阮秋琦，译.北京:电子工业出版社，2005:290－292.

Improved edge thinning method

XU Hong －ke，QIN Yan －yan，PAN Yong
(School of Electronic and Control Engineering，Chang'an University，Xi'an 710064，China)

An improved edge thinning method with adaptive smooth filter is proposed for de－noising and thinning rough edge detected by Sobel operator.A new gradient operator is used for adaptive smooth filter，which can overcome noise influence and sharpen image edge effectively.Then，the improved edge thinning method is used after edge detection with Sobel operator.Experimental results show that the new gradient operator is better than the old one with the same iteration number，and the improved edge thinning method can preserve more edge details with a considerable calculation time meanwhile.

image processing;edge thinning;adaptive smooth filter;Sobel operator;edge detection

TP391.41

A

10.3969/j.issn.1001－5078.2014.03.22

1001－5078(2014)03－0319－06

国家山区公路工程技术研究中心开放基金项目(No.gsgzj－2011－08)资助。

许宏科(1963－)，男，博士，教授，研究方向为交通图像处理。

2013－07－10