一种组合隶属度函数及其在电能质量模糊评价中的应用

杨家豪，欧阳森，石怡理，黄瑞艺，刘子文

(华南理工大学电力学院，广东 广州510640)

1 引言

模糊综合评价方法是国内外的电能质量评价的主要手段之一［1-8］。其运用于电能质量的评价，关键在于隶属度函数的选择和设计。在实际评价过程中，选择不同的隶属度函数会导致评价结果出现差异，因此设计一种具有普遍适用性的隶属度函数来提高评价结果的可信度具有重要意义。

文献［2-5］中隶属度函数的参数的确定需要依靠实际情况和个人的经验进行反复设计，使评价结果具有人为主观性而导致可信度降低;文献［6，10］选择了单一的岭形或三角形隶属度函数，根据最大隶属度原则和极限原则确定左右零点，没有考虑隶属度函数的选择对评价结果的影响;文献［7］中采用数学拟合并修正后得到隶属度函数中参数，这种方法的可信度受到曲线拟合精度的限制。文献［9］中采用Bezier曲线逼近方式，当曲线的幂次较低时效果较差，此时灵活性受到限制，且控制点数目会对拟合出的隶属函数精度造成影响。

优选组合方法在预测领域得到了广泛的应用，在许多文献中已经验证“组合预测模型的预测误差平方和不大于参与组合的各个单一模型的预测误差平方和的最小者”［11，12］。因此组合的结果可以有效减小波动，提高稳定性，同时其适用性必然是最好的。

针对不同隶属度函数会导致评价结果出现差异的问题，本文拟选取五种典型隶属度函数进行模糊评价，再引入方差—协方差优选组合法［12］，对五种典型的隶属度函数进行赋权组合，构造出一种组合隶属度函数。方差—协方差优选组合法对所选取的隶属度函数的评价信息实现了充分利用，对多种单一模糊评价模型所包含的信息进行最优组合，从而使组合隶属度函数具有普遍适用性，最终使评价结果充分可信。文章最后给出一个算例，通过实例验证了本算法的有效性。

2 典型隶属度函数分析

设在论域U上给定一个映射:

A:U→［0，1］

u a A(u)

则称A为U上的模糊集;A(u)称为A的隶属度函数(或称为u对A的隶属度)。

隶属度函数又可以分为:偏小型、中间型、偏大型。偏小型和偏大型只是单侧区间有值，而中间型的特点是区间对称有值。由于电能质量评价涉及到的指标较多，为了使选取的隶属度函数均能适用于各个指标的评价，提高普遍适用性，故本文均采用中间型隶属度函数，保证其对称性和平衡性［13］。

本文选取五种典型的隶属度函数作为构造组合隶属度函数的基础，如表1所示。由表1可知，每一种隶属度函数都具有自身的特点，当选用不同的隶属度函数进行模糊评价时，得到的隶属度必然不同，从而导致评价结果出现差异。同时，每个隶属度函数中又含有一个或两个待定的参数(表达式中a、b均为待定参数)，同样的隶属度函数，只要参数的设计不同，亦会导致隶属度出现差异。因此，在单一隶属度函数下得到的评价结果可信度不高。

表1 五种典型的隶属度函数Tab．1 Fivetypicalmembershipfunctions

3 基于优选组合法的隶属度函数构造

3.1 同一评价指标的隶属度平均值

先求取同一指标在不同隶属度函数下的隶属度，再求取这些隶属度的平均值:

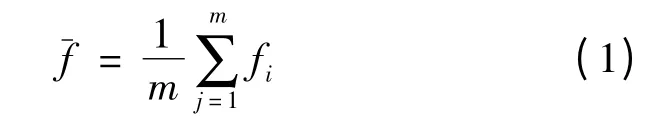
式中，fi表示该指标在第i个隶属度函数下的隶属度值;m表示总共有m种隶属度函数，本文中m=5。

3.2 方差—协方差优选组合法

设f1，f2是在两个不同隶属度函数下关于f－的无偏隶属度值，fc是加权平均的组合隶属度值，偏离f－的误差分别为e1，e2和ec。w1和w2是相应的权系数，且w1+w2=1，则有:fc=w1f1+w2f2，若fc也为无偏的，则可以证明:ec=e1+e2，从而有fc的方差为:

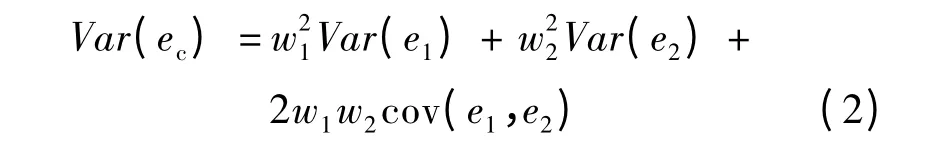
关于w1对Var(ec)求极小值，可得:

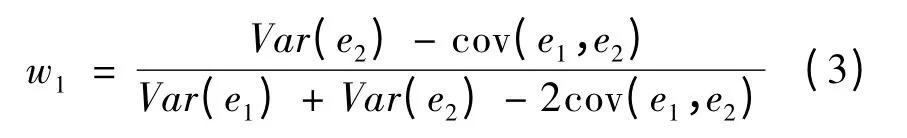
又w2=1－w1，记方差Var(e2)=σ22，Var(e1)=σ11，协方差cov(e1，e2)=σ12。由于e1、e2相互独立，则σ12=0，有:

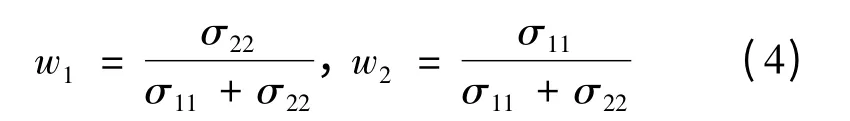
把两种隶属度函数的组合结果一般化。设m个无偏隶属度值分别为f1，f2，．．．，fm，各自相对于f－的误差的方差为σ11，σ22，．．．，σkk。在许多实际情况下，不同隶属度函数之间的误差是不相关的。关于wi(i=1，2，．．．，m)对Var(ec)求极小值是个求条件极值的问题，在约束条件∑wi=1的条件下，对Var(ec)引入Lagrange乘子来求极小值，可以得到各个隶属度函数的权重:

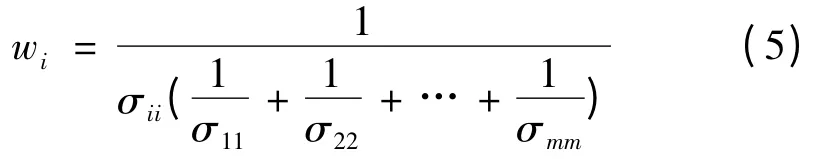
式中，i=1，2，…，m。

由此可见，隶属度值越靠近平均值f－的隶属度函数，即方差越小其权重就越大。

3.3 组合隶属度函数

根据上面求得的各个隶属度函数的权重，构造组合隶属度函数，如下:

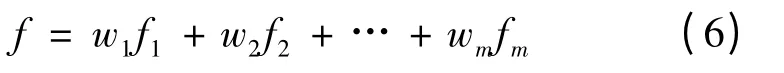
从式(6)可知，新构造的组合隶属度函数f对五种隶属度函数进行优化整合，突出评价结论一致性较高的部分隶属度函数的作用，同时兼顾一致性程度较低的另一部分函数所承载的评价信息，即仅弱化其作用，而不完全剔除该信息，从而既对评价结论相对一致的多评价结果进行了优化组合，又充分利用了所有的评价方法信息，最终使应用组合隶属度函数进行评价所得的评价结果的可信度更高。

4 电能质量模糊评价算法设计

4.1 电能质量指标权重的确定

本文侧重于使用组合隶属度函数实现对评价结果的优化，故在权重的确定上并没有强制性的要求，为不失一般性，拟采用G1法(序关系分析法)［14］来确定电能质量指标的权重，该方法过程清晰简便，能充分体现专家的意愿。主要指标包括电压偏差、频率偏差、谐波电压总畸变率、三相电压不平衡度以及电压闪变5项。步骤如下:

(1)首先确定序关系。设对于某评价准则指标的重要程度具有的序关系x1≻x2≻···≻xm。

(2)然后确定相邻指标之间的相对重要程度。设专家关于评价指标xk－1与xk的重要程度之比wk－1/wk的理性判断分别为:

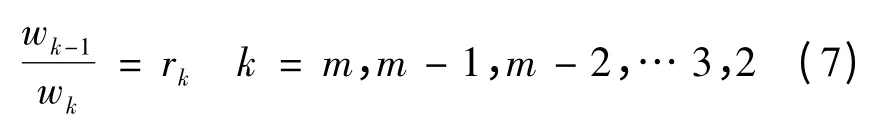
其中，对xk－1与xk的重要程度之比的判断分为五种情况，分别对应不同的rk，其赋值可参考表2。

(3)最后计算权重系数wk:

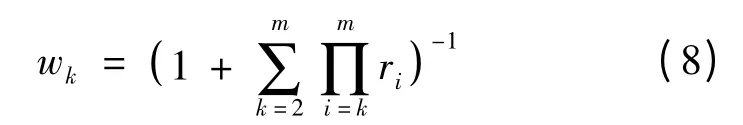
由wk得出其他指标的权重:

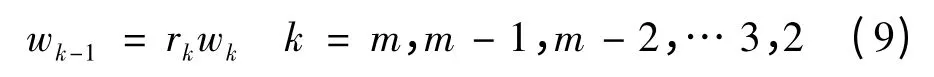
表2 rk赋值参考表Tab．2 Assignment reference of rk

4.2 电能质量评价

在选定的隶属度函数下，可得到对应的模糊隶属矩阵:

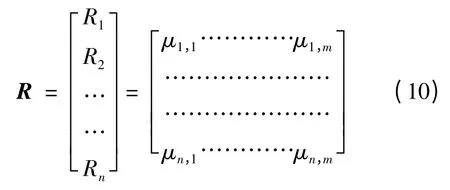
式中，n为电能质量指标数;m为质量等级数;Ri为第i项指标的单因素评价。

矩阵里的μi，j须进行归一化处理，即为:

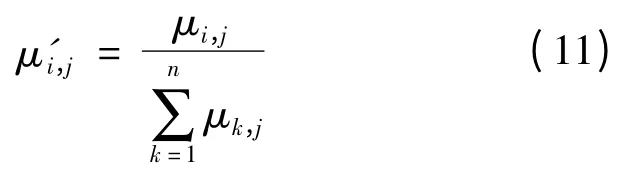
最后的评价结果为:其中，W为电能质量指标权重矢量，W=(w1，w2，…，wm);B为相对于各质量等级隶属度向量。

对5个质量等级依次赋以分值c1=5、c2=4、c3=3、c4=2、c5=1，分别代表“优质”、“良好”、“中”、“合格”、“不合格”，最后采用加权平均得到评价点的电能质量评价值:

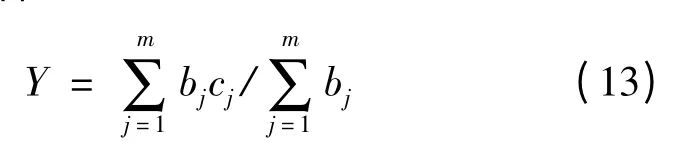
4.3 算法步骤

利用方差—协方差法对选定的五种隶属度函数进行优化组合，从而构造出组合隶属度函数并进行模糊评价。算法包括五个步骤:

(1)进行电能质量等级划分。

(2)利用G1法来确定电能质量指标的权重。

(3)分别利用五种典型的隶属度函数计算电能质量各指标数据的隶属度值，利用式(1)计算各指标的隶属度值的平均值。

(4)利用式(5)计算各隶属度函数对于各电能质量指标的权重。

(5)利用式(6)构造出相对于各个指标的组合隶属度函数;同时利用组合隶属度函数计算各电能质量指标数据的隶属度值。

(6)利用式(10)、式(11)分别计算在五种隶属度函数和组合隶属度函数下的模糊评价矩阵R。

(7)利用式(7)～式(9)计算电能质量指标权重W。再利用式(12)得到隶属度向量;再通过式(13)进行加权平均得到评价值。

5 实例分析

5.1 计算过程

应用五种典型隶属度函数和组合隶属度函数对某变电站电能质量数据进行模糊评价，并进行对比分析。本文划分的电能质量等级如表3所示。

表3 电能质量指标及其质量等级划分准则Tab．3 Power quality indexes and their division norms of quality level

本文数据来源于广州供电局某110kV变电站1～12月的电能质量数据，如表4所示。根据表3中的电能质量数据，利用5种典型的隶属度函数计算每一个数据关于各电能质量等级的隶属度值，再利用式(1)和式(5)计算各个隶属度函数在每一个电能质量指标下的权重，如表5所示。

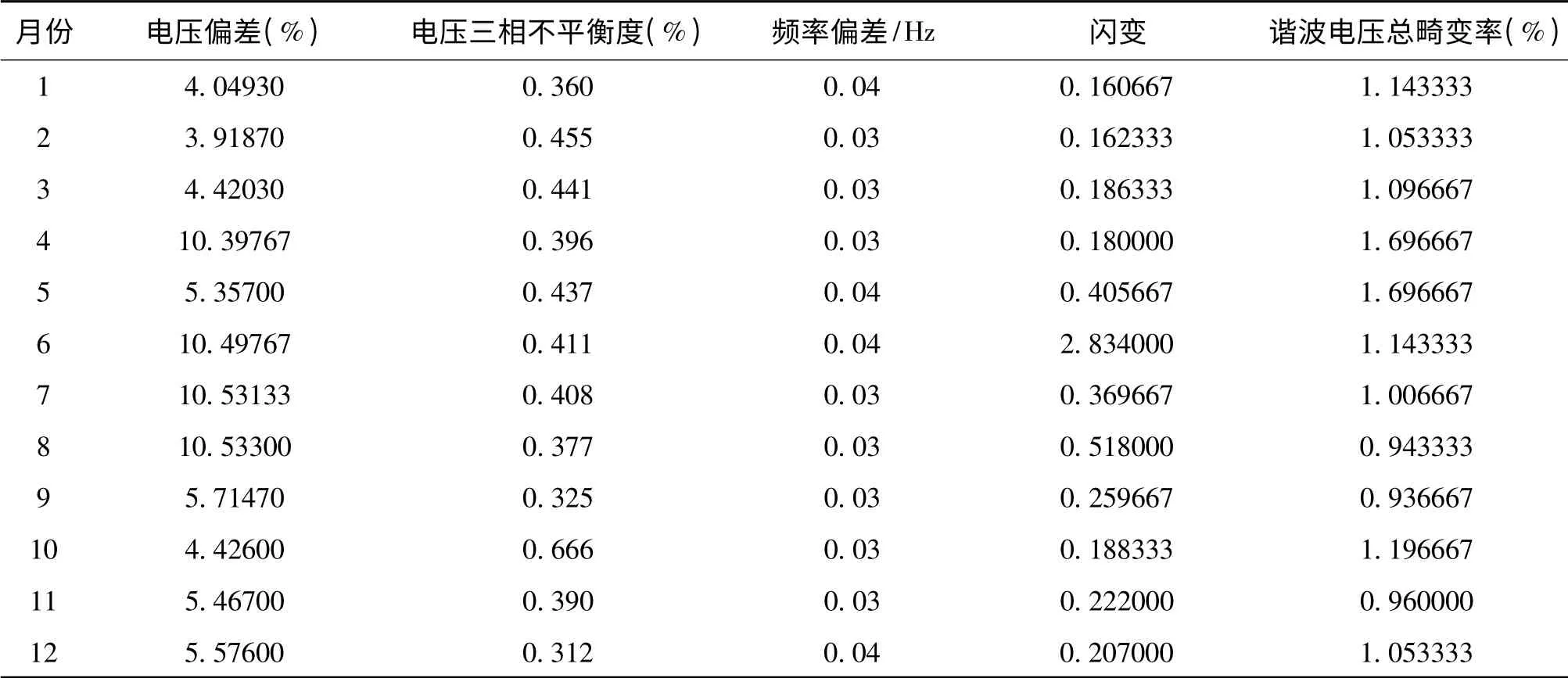
表4 变电站电能质量数据Tab．4 Power quality data of substation

表5 各电能指标下5种隶属度函数的权重Tab．5 Weights of fivemembership functions of each power indicator

从而根据式(6)计算各电能质量指标的组合隶属度函数，再利用组合隶属度函数计算每一个数据关于各质量等级的隶属度值。

电能质量指标按照“谐波电压总畸变率≻电压偏差≻电压闪变≻三相电压不平衡度≻频率偏差”的序关系，利用G1法得出各电能质量指标权重为W=(0.2728，0.248，0.206667，0.15897，0.1135);分别把5种隶属度函数的隶属度值和组合函数算得的隶属度值代入式(10)中得到每月关于不同隶属度函数的模糊评判矩阵，再利用式(11)～式(13)得到每个月的关于不同隶属度函数的模糊评价结果，如表6和图1所示。

其中，Y1在岭型分布隶属度函数下12个月的评价值，Y2在尖Γ分布隶属度函数下12个月的评价值，Y3在柯西分布隶属度函数下12个月的评价值，Y4在梯形分布隶属度函数下12个月的评价值，Y5在正态分布隶属度函数下12个月的评价值，Y6在组合隶属度函数下12个月的评价值。

5.2 结果分析

从表6和图1可知，五种典型的隶属度函数算出来的12个月模糊评价值分布在2.8～3.5之间;而评价值等于3时，是电能质量等级“中”和“合格”的分界线，这时就会出现在某个隶属度函数下该月的电能质量等级为“中”，而在另一隶属度函数下为合格的现象，因而导致评价结果具有不确定性。此时，基于优选组合的隶属度函数，对各隶属度函数进行了最优组合，必然比单一隶属度函数的评价结果更具有可信性。

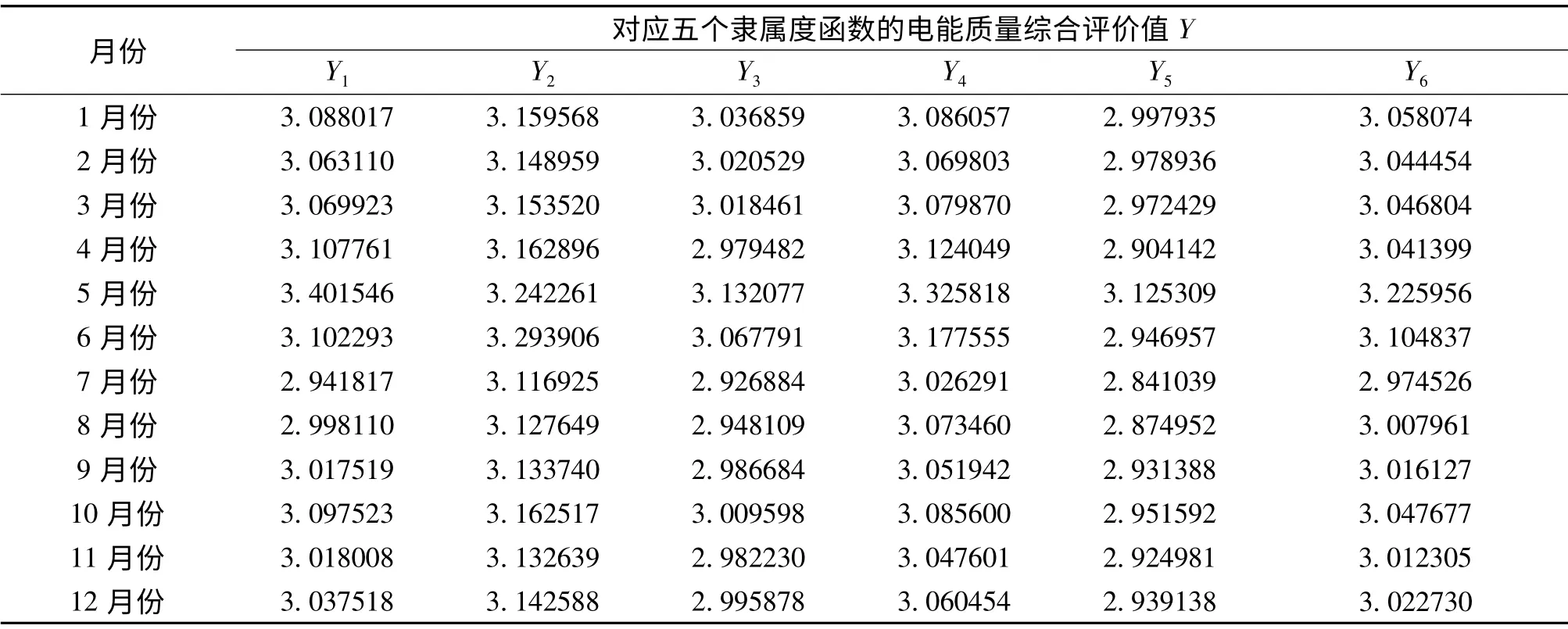
表6 对应各个隶属度函数的12个月电能质量综合评价值YTab．6 Power quality comprehensive evaluation value Y of12 months corresponding to each membership function

(1)从表6可以看出，4月份的评价值中，隶属度函数为柯西分布和正态分别时分别比3小0.0205和0.0959，而隶属度函数为岭型分布、尖Γ分布和梯形分布分别比3大0.1078、0.163和0.124，综合来看，4月份的评价值更趋向于大于3，即电能质量等级为中;利用组合隶属度函数算出的评价值3.041399，验证了上述分析，因此有理由相信4月份的电能质量的质量等级为中更可信。同样，对于7月份，有三个评价值小于3，两个评价值大于3，且小于3的评价值偏离“合格”的程度高于大于3的评价值，因此，类似4月份的分析过程，7月份评价值应小于3，即电能质量等级为“合格”;利用组合隶属度函数算出的评价值2.974526，也验证了上述分析。对于其他月份，进行类似的分析，可以得到类似的分析结果。

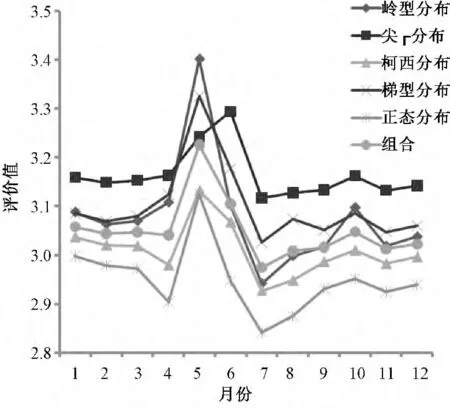
图1 对应各个隶属度函数的12个月电能质量综合评价值YFig．1 Power quality comprehensive evaluation value Y of 12 months corresponding to eachmembership function

(2)由图1可以看出，优选组合分布的评价结果分布在五种隶属度函数评价结果中间，类似于评价结果取了平均值，使评价结果的可信度提高。必须指出，这与单纯计算评价值的平均值存在本质区别，因为方差—协方差优选组合法是从隶属度层面进行赋权的，当某一隶属度函数算出的隶属度值偏离平均隶属度值很大时，认为该隶属度函数不够精确，因而赋予的权重相应就小，反之亦然。通过对隶属度函数加权得到了组合隶属度函数更准确，从而提高了评价结果的可信度。

6 结论

在电能质量模糊评价过程中，隶属度函数的选择问题由于人为的主观性及经验性太强，要得到一个让所有人都认可的结果近乎不可能。将基于多种隶属度函数的评价结果通过赋予不同的权重来综合分析是非常有益的尝试。

本文引入方差—协方差最优组合法，对五种典型隶属度函数进行最优组合，构造了具有普遍适用性的组合隶属度函数，其中突出了评价结论一致性较高的那部分隶属度函数的作用，同时兼顾一致性程度较低的另一部分函数，仅起将其弱化的作用，而不完全剔除该方法，充分利用了五种典型函数的评价信息，使模糊评价结果的可信度得到提高。

本文所提出的算法很好地处理了单一隶属度函数导致评价结果出现的差异性。通过实例分析验证了本文算法的有效性。

［1］Farghal SA，Kandil M S，Elmitwally A．Quantifying electric power quality via fuzzymodeling and analytic hierarchy processing［J］．IEEE Proceedings Generation Transmission and Distribution，2002，149(1):44-49．

［2］贾清泉，宋家骅，兰华，等(Jia Qingquan，Song Jiahua，Lan Hua，etal．)．电能质量及其模糊方法评价(Power quality and fuzzymethod evaluation)［J］．电网技术(Power System Technology)，2000，24(6):46-49．

［3］赵 霞，赵 成 勇，贾 秀 芳，等(Zhao Xia，Zhao Chengyong，Jia Xiufang，et al．)．基于可变权重的电能质量模糊综合评价(Fuzzy synthetic evaluation of power quality based on changeable weight)［J］．电网技术(Power System Technology)，2005，29(6):11-16．

［4］李连结，姚建刚，龙立波，等(Li Lianjie，Yao Jiangang，Long Libo，et al．)．组合赋权法在电能质量模糊综合评价中的应用(Application of combination weighting method in fuzzy synthetic evaluation of power quality)［J］．电力系统自动化(Automation of Electric Power Systems)，2007，31(4):56-60．

［5］蒋金良，袁金晶，欧阳森(Jiang Jinliang，Yuan Jinjing，Ouyang Sen)．基于改进隶属度函数的电能质量模糊综合评价方法研究(Research of fuzzy synthetic evaluation method of power quality based on improved membership function)［J］．华南理工大学学报(Journal of South China University of Technology)，2012，40(11):107-112．

［6］谭家茂，黄少先(Tan Jiamao，Huang Shaoxian)．基于模糊理论的电能质量综合评价方法研究(Study on power quality comprehensive evaluation based on fuzzy theory)［J］．继电器(Relay)，2006，34(3):55-59．

［7］唐会智，彭建春(Tang Huizhi，Peng Jianchun)．基于模糊理论的电能质量综合量化指标研究(Research on synthetic and quantificated appraisal index of power quality based on fuzzy theory)［J］．电网技术(Power System Technology)，2003，27(12):85-88．

［8］陶顺，肖湘宁(Tao Shun，Xiao Xiangning)．基于短板效应的电能质量综合等级评价(Synthetic grading evaluation of power quality based on incentivemechanism)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2008，27(2):16-20．

［9］Medaglia A L，Fang SC，Nuttle H LW，et al．An efficient and flexiblemechanism for constructing membership function［J］．European J of Operational Research，2002，139(1):84-95．

［10］汪金刚，张作鹏，龙震泽，等(Wang Jingang，Zhang Zuopeng，Long Zhenze，etal．)．采用模糊推理对绝缘子放电紫外检测结果进行外绝缘放电状况评估(Discharge status evaluation on external insulation of insulator based on results of ultra-violet radiation measurement and fuzzy reasoning)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2011，30(2):79-83．

［11］汪同三，张涛(Wang Tongsan，Zhang Tao)．组合预测:理论、方法及其应用(Forecast combination:theory，method and application)［M］．北京:社会科学文献出版社(Beijing:Social Sciences Academic Press)，2008．

［12］康重庆，夏清，刘梅(Kang Chongqing，Xia Qing，Liu Mei)．电力系统负荷预测(Power system load forecasting)［M］．北京:中国电力出版社(Beijing:China Electric Power Press)，2007．

［13］王季方，卢正鼎(Wang Jifang，Lu Zhengding)．模糊控制中隶属度函数的确定方法(The determine method ofmembership function in fuzzy control)［J］．河南科学(Henan Science)，2000，18(4):348-351．

［14］郭亚军(Guo Yajun)．综合评价理论、方法及应用(Comprehensive evaluation theory，methods and application)［M］．北京:科学出版社(Beijing:Science Press)，2007．