优化的准正弦平顶调制波PWM新技术

王榕生，汤宁平，林 珍，黄灿水

(福州大学电气工程与自动化学院，福建 福州350108)

1 引言

评估一种PWM技术有三个方面标准:①最大输出线电压基波幅值;②电流谐波总失真度THD;③PWM实时算法。根据该标准对现有三相PWM技术综述如下。

①SPWM技术因采用正弦调制波使得PWM输出不含有低次谐波，只含有载频及其倍数附近的谐波，其THD值低，但直流电压利用率(最大输出线电压基波幅值与直流电压之比)低［1-3］，仅为0.866;②电压空间矢量SVPWM技术因其直流电压利用率达到1，比SPWM高15%而广为应用，但其PWM算法须确定输出电压矢量Uout所在扇区号而较为复杂［4-6］;③指定谐波消除SEHPWM技术可以消除对负载影响大的低次谐波，使功率器件在较低的开关频率条件下最大限度地消除低次谐波对电机电流、转矩的影响［7，8］，其直流电压利用率可以达到π/4，然而其PWM算法因涉及求解超越方程，计算耗时多，尚难达到实时计算的应用要求;④三次谐波注入法PWM对正弦调制波叠加适当大小的三次谐波分量以提高所包含的基波分量，合成线电压时三次谐波分量相互抵消，其直流电压利用率较SPWM提高15%［1，2］，但难以满足进一步提升直流电压利用率的应用要求。

综上所述，提升PWM最大输出基波幅值且具有相对简单的PWM算法和较低的电流谐波总失真度THD一直是人们追求的目标。为此，本文尝试构建一种称之为“准正弦平顶新调制波”，在对三角载波调制后所生成的三相PWM能显著提升最大输出线电压基波幅值，且具有相对简单的PWM实时算法和较低的THD。由数值分析与实验结果证实了新方法的有效性。

2 准正弦平顶调制波

为提高调制波所含基波分量，构建一种新型调制波如图1所示。

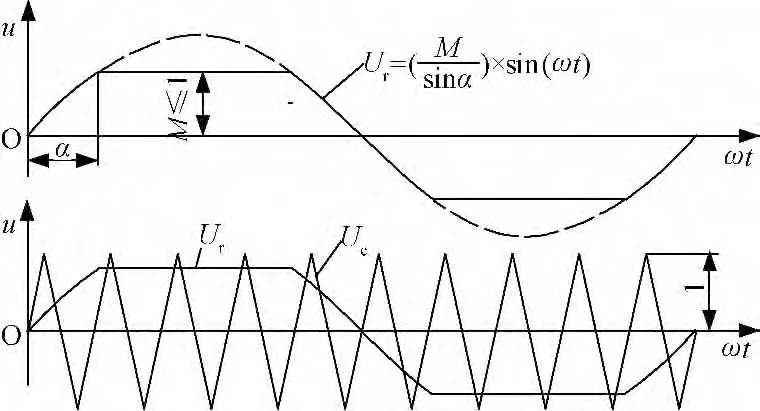
图1 准正弦平顶调制波Fig．1 Flat top quasi-sinusoidalmodulating waveform

图1所示调制波Ur是将正弦波顶部削去后得到的波形，其特征为中间部分为平顶波，两腰为正弦波。对该波形的数学描述如下:式中，M为平顶高，0≤M≤1;α为两腰宽，0＜α≤π/2。因图1中的三角载波幅值取1，所以调制波平顶高M等同于调制度。

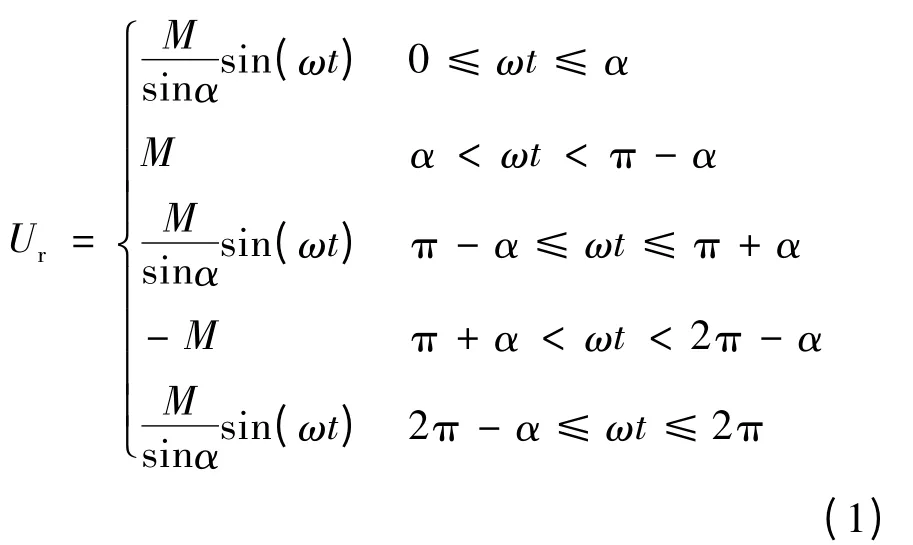
由傅里叶分析可知，式(1)调制波所含基波分量幅值大于平顶高度M，并随着调制波平顶宽度的增大即α角的减小而增大。当α→0时，调制波演变为方波，其基波幅值达π/4。虽然扩大平顶宽度带来了提高基波分量幅值的好处，但另一方面，所含谐波分量亦随平顶宽度的增大(即α角减小)而有起伏变化。为获取最佳调制波，必须解决好增大基波与降低谐波影响二者间的矛盾。谐波影响由谐波失真度来衡量，定义如下:

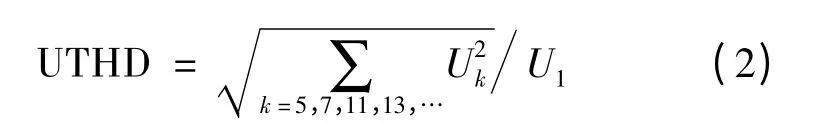
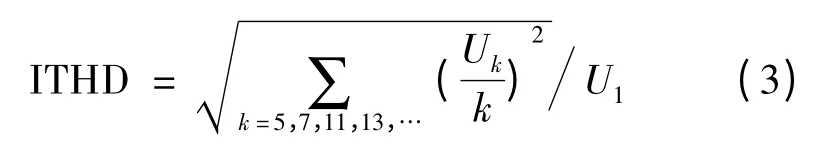
电压谐波失真度电流谐波失真度式中，Uk为k次电压谐波幅值;U1为电压基波幅值。因图1调制波具有1/4周波对称而不含偶次谐波，且线电压中也不含有三次及其倍数次谐波，所以k为非三倍次的奇次谐波次数。

图2、图3分别给出了当M=1时基波及有影响的低次电压谐波失真度UTHD与电流谐波失真度ITHD(累计谐波至53次)随α变化曲线。图4为5、7、11、13次谐波随α变化曲线。

由图2～图4表明，随着α的减小即平顶宽度的增大，必伴生出谐波影响，这是增大基波分量的代价。然而客观上存在着择优空间，可在其间寻求一个最优点，即在提升基波分量的过程中寻求谐波影响相对最小。不难看出，当α=0．658时，ITHD有一个极小值，对应的基波幅值达1.19，并且UTHD也在该点附近取得极小值。所含有的5、7、11、13等有影响的低次谐波幅值如表1所示，其中影响最大5次谐波为0，7次谐波幅值仅0.0337。综合所有情况，可认为在α=0．658取值下的调制波为最佳。

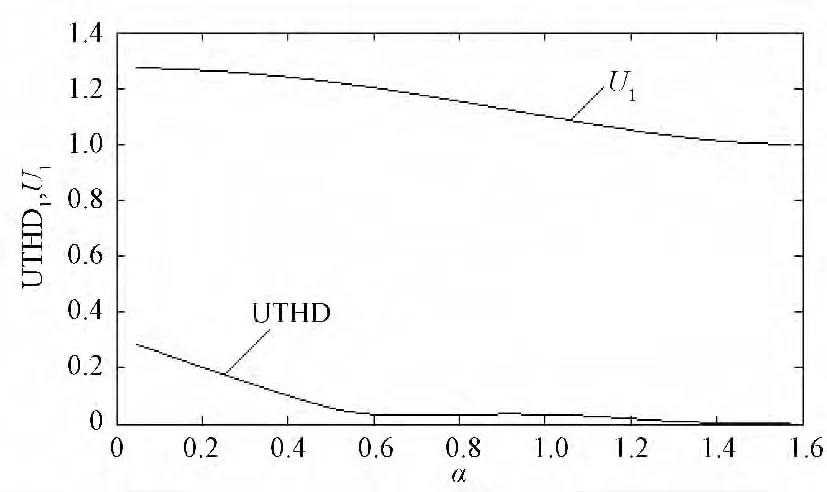
图2 UTHD与基波分量U1随α变化曲线Fig．2 Variation of UTHD and fundamental component U1 withα

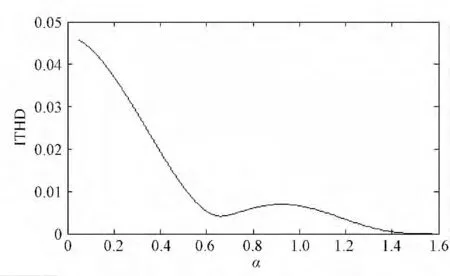
图3 ITHD随α变化曲线Fig．3 Variation of ITHD withα

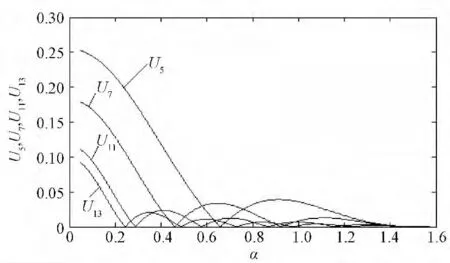
图4 5、7、11、13次谐波随α变化曲线Fig．4 Variation of 5th、7th、11th、13th harmonic componentswithα

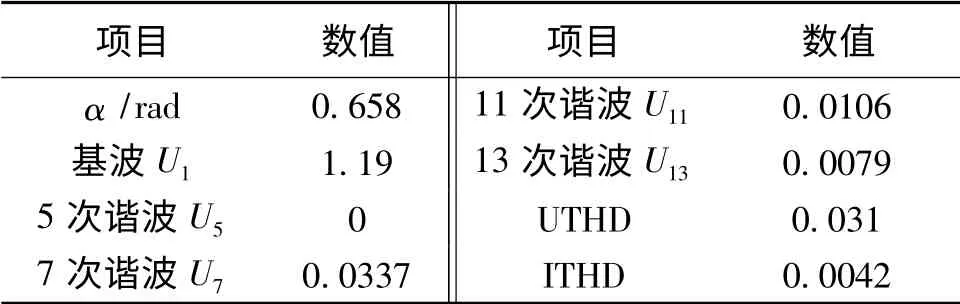
表1 各谐波分量及谐波失真度值Tab．1 Harmonic component and THD

3 PWM算法

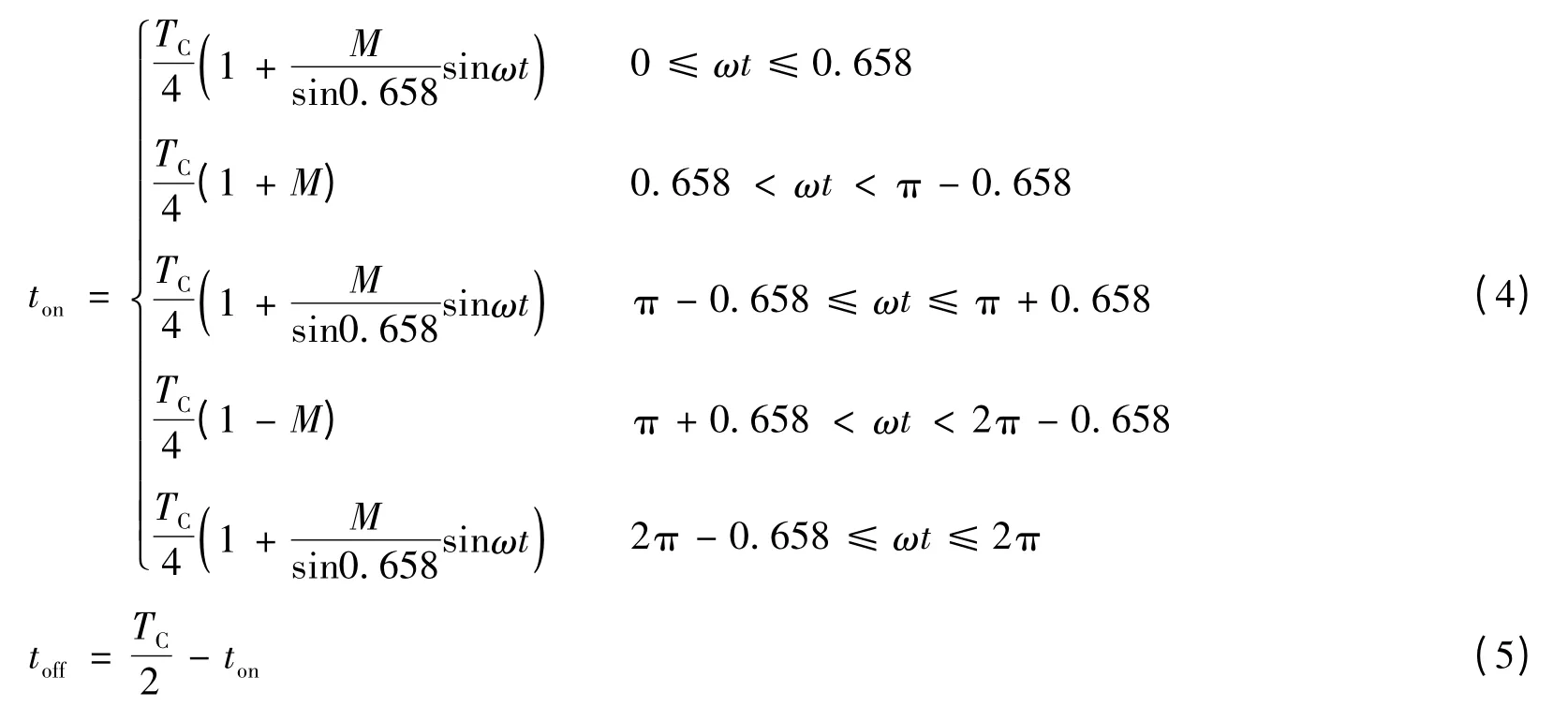
确定了最佳调制波之后，对三角载波进行调制，所得到的三相PWM的最大输出线电压基波幅值将比SPWM高19%。如采用不对称规则采样法，其PWM脉冲计算公式如下:式中，ton与toff分别为每半个载波周期TC/2内的脉宽时间与间歇时间;TC=2π/(ωN)为载波周期;N=fC/f为载波比;ω=2πf为调制波角频率;M=Urm/Utm为调制度;t为载波峰顶或谷底采样时刻。不难看出，由式(4)和式(5)所表述的PWM算法只比SPWM增加了调制波采样角所在区间判别以及据此选择不同脉冲计算公式的环节。对公式中的1/sin0.658项可预先求值作为常量处理。由式(4)、式(5)计算出PWM线电压波形如图5所示。

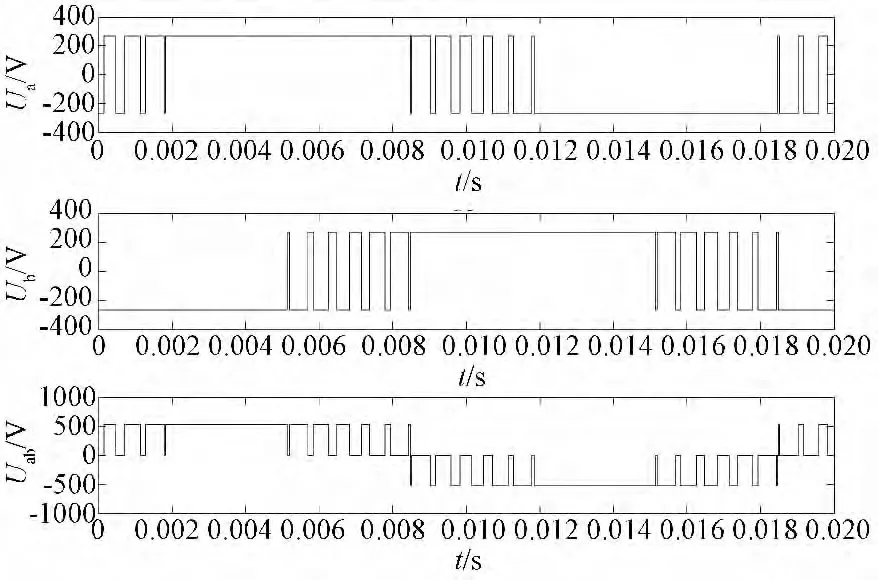
图5 PWM线电压波形(N=33，f=50Hz，M=1)Fig．5 PWM line-voltage waveforms(N=33，f=50Hz，M=1)

4 谐波数值分析

由调制波的波形特征决定了其PWM线电压所含谐波为非3倍数的奇次谐波群，对此可根据以下傅里叶公式加以计算。式中，A0为直流分量;Ak为k次谐波余弦分量;Bk为k次谐波正弦分量;ω=2π/T为基波角频率。

取载波比N=33，在全电压范围内计算线电压基波及各次谐波。图6示出了准正弦平顶调制波PWM线电压基波及有影响的N±2、N±4、2N±1等次谐波的相对值(幅值/基值)随M的变化关系，各分量均以直流母线电压Ud为基值。为使同一M值下的基波电压与SPWM的相同以便于对比，将横坐标M按图1准正弦平顶调制波含有的最大基波幅值与三角载波幅值的比值予以放大(下同)。

作为对比，给出了SPWM线电压基波及主要谐波分量与调制度M的关系，如图7所示。

图6与图7有相同的载波比N=33，即开关频率相同。对比显示两种PWM的2N±1次谐波基本相同，且N±2次谐波有相同变化趋势。但图6的PWM所含谐波相对丰富，有影响的谐波比图7多出了N±4次。然而另一方面，在M∈［0，1］范围内，图7的N±2次谐波值明显大于图6的同次谐波，当M=1时，其幅值比图6同次谐波大43%以上。纵观两种PWM的谐波群，可以看出准正弦平顶调制波PWM的谐波呈现“多而小”的特征，而SPWM则呈现“少而大”的特征。为得出两种PWM谐波总影响，通常办法是按式(2)和式(3)分别求出UTHD及ITHD。

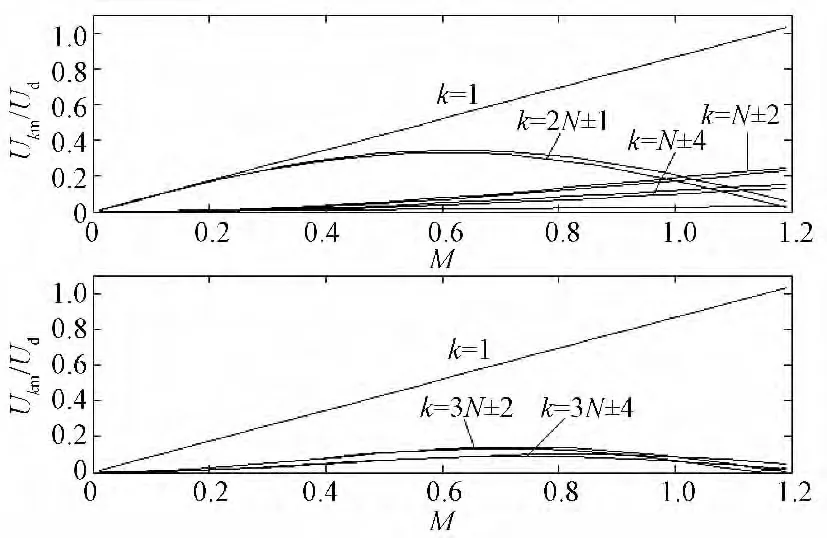
图6 N±2，N±4，2N±1、3N±2、3N±4次电压谐波分量与M的关系(N=33)Fig．6 Variation of N±2，N±4，2N±1、3N±2、3N±4 voltage harmonic componentwith modulation index M(N=33)

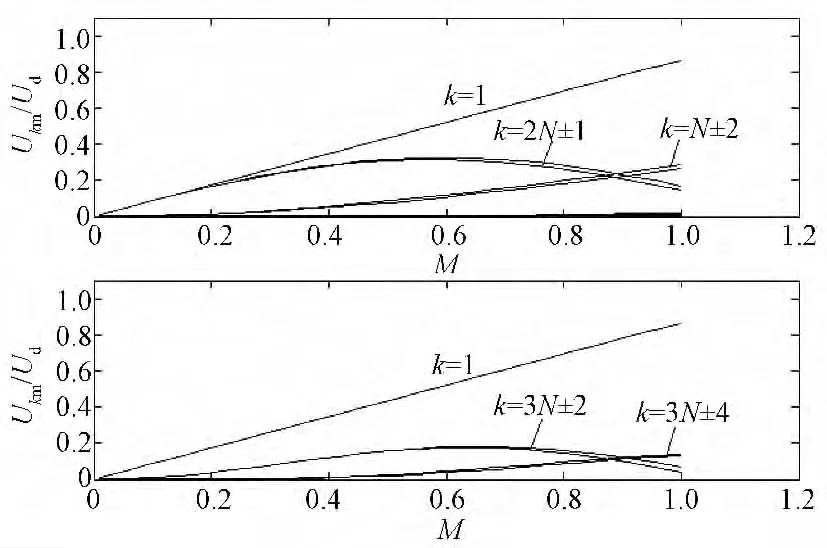
图7 不对称规则采样SPWM电压谐波分量与调制度M的关系(N=33)Fig．7 Variation of voltage harmonic component with modulation index M for asymmetric regular sampling(N=33)

图8示出了准正弦平顶调制波PWM与SPWM在载波比N=33的全电压范围的UTHD及ITHD变化曲线(累计谐波至200次)。二者UTHD值很接近，而ITHD值对比大体以M=0．55为界，当调制度M＞0．55时，准正弦平顶调制波PWM线电压ITHD值小(优)于SPWM的ITHD;而当M＜0．55时，其ITHD值转为大于SPWM，但最大增加量不超过2.2%。因此，二者在M∈［0，1.19］全电压范围的ITHD指标平分秋色。

5 实验验证

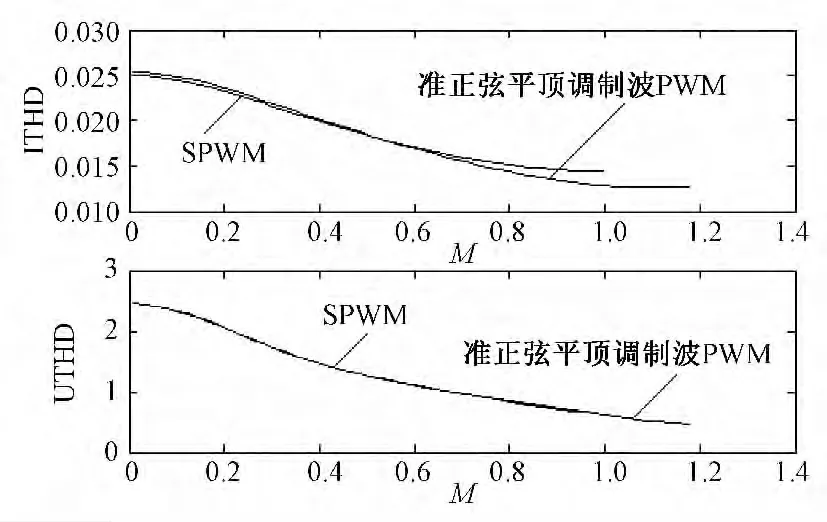
图8 两种PWM的ITHD及UTHD对比(N=33)Fig．8 Comparison of ITHD and UTHD curves with two PWM(N=33)

为验证新技术有效性，搭建了以TMS320LF2407A为控制核心的三相电压型逆变系统，按式(4)和式(5)算法编制了三相PWM的DSP控制软件，其载波频率为1.65kHz，死区时间4.2μs。直流母线电压311V，负载电机功率为1.1kW。图9为实测的PWM线电压与线电流波形。

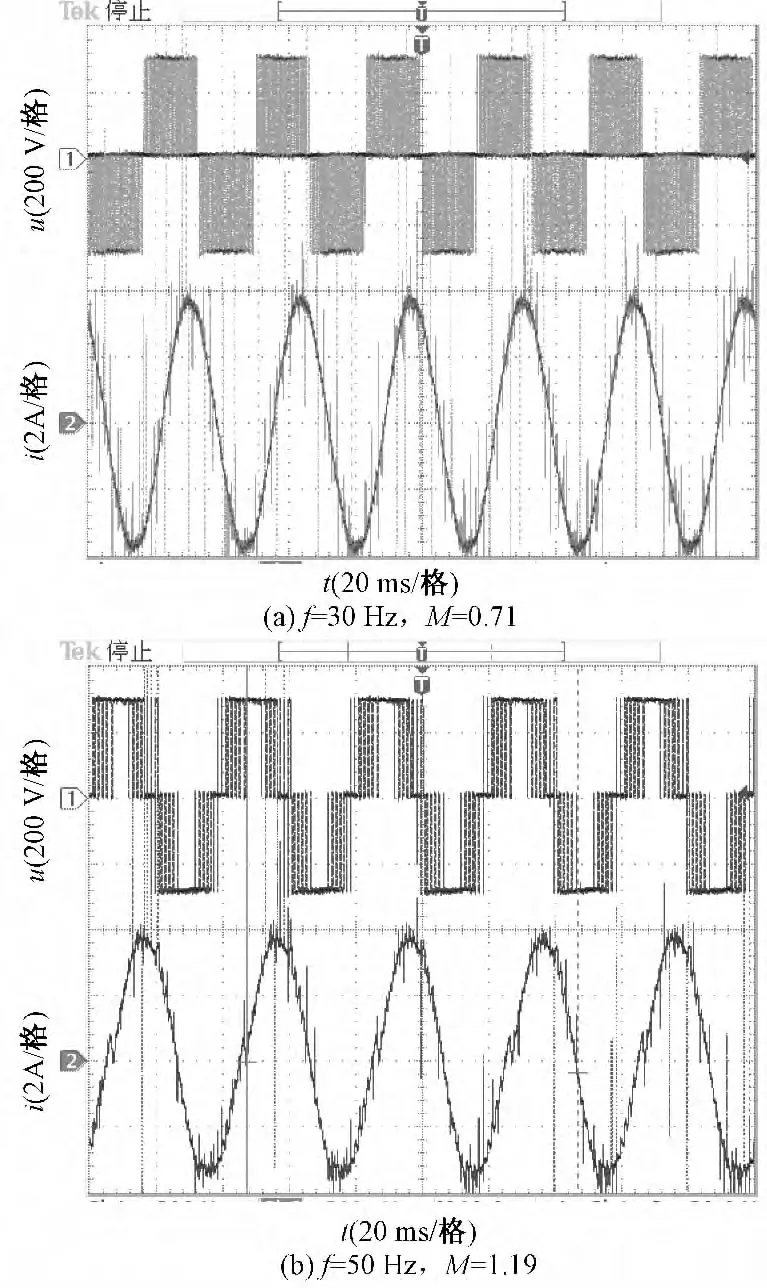
图9 负载线电压与线电流实测波形Fig．9 Measurement of load line-voltage and line-currentwaveforms

表2示出了图9(b)的最大输出线电压基波及各次谐波幅值的实测与计算值。其中基波及有影响的载频附近的N±2、N±4次主要谐波值具有良好吻合。由于实测PWM存在“死区”，其作用相当于在理想的PWM输出电压上叠加了一系列窄脉冲而使波形发生畸变，出现少量的5次谐波，以及那些数值较小的谐波值也有所变化。除“死区”影响外，母线直流电压的脉动以及DSP器件只能对数据进行定点处理等因素也是引起波形失真的原因。

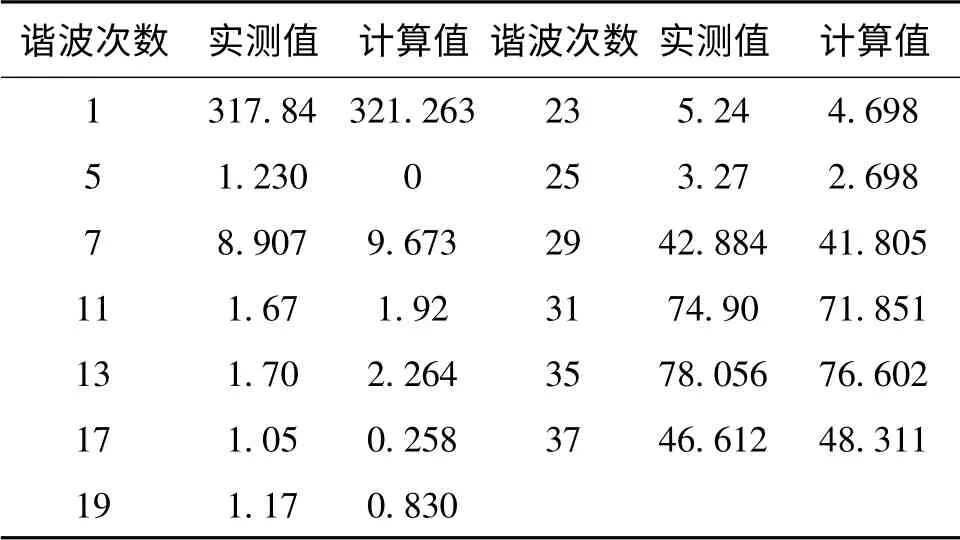
表2 线电压基波与谐波幅值(M=1.19，N=33)Tab．2 Line-voltage fundamental and harmonic component amplitude(M=1.19，N=33)

所述的DSP控制软件在其他调制度M或调制波频率f取值下，均实现良好的输出电流波形，限于篇幅图略。

6 结论

(1)通过对所构建的准正弦平顶调制波进行优化，使α=0．658，不仅显著增大了调制波所含基波幅值，而且使伴生出的谐波分量得以有效抑制;

(2)采用不对称规则采样法对三角载波进行调制，其PWM算法只比SPWM增加了调制波采样角所在区间判别以及据此选择不同脉冲计算公式的环节，因此，仍不失为简单的PWM算法;

(3)所得三相PWM基波分量与调制度M间有严格的线性关系，其最大输出线电压基波幅值比SPWM高19%，比SVPWM高3.2%，电流谐波总失真度ITHD在调制度M∈［0.55，1］区间低于SPWM的相应值，虽然在M∈［0，0.55］区间高于SPWM，但增量不超过2.2%。实验结果证实了新技术的有效性。

［1］Sidney R Bowes，Derrick Holliday．Optimal regular-sampled PWM inverter control techniques［J］．IEEE Transactions on Industrial Electronics，2007，54(3):1547-1559．

［2］SR Bowes，D Holliday．Comparison of pulse-width-modulation control strategies for three-phase inverter systems［J］．IEE Proc．Electr．Power Appl．，2006，153(4):575-584．

［3］王榕生(Wang Rongsheng)．线性组合采样法SPWM新技术(A novel linear combination sampling SPWM technique)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2010，29(2):29-32．

［4］方斯琛，李丹，周波，等(Fang Sichen，Li Dan，Zhou Bo，et al．)．新型无扇区空间矢量脉宽调制算法(A novel algorithm of space-vector PWM without sector calculation)［J］．中国电机工程学报(Proceedings of the CSEE)，2008，28(30):35-40．

［5］万健如，程传更，张海波，等(Wan Jianru，Cheng Chuangeng，Zhang Haibo，et al．)．一种新颖的混合空间矢量控制方法(A novel hybrid space vector control method)［J］．中国电机工程学报(Proceedings of the CSEE)，2006，26(5):101-104．

［6］王永，沈颂华，吕宏丽，等(Wang Yong，Shen Songhua，Lv Hongli，et al．)．基于简单电压空间矢量三相逆变器的研究(Study of three-phase inverters based on simplified voltage space-vectormethod)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2005，20(10):25-29．

［7］王榕生，吴汉光(Wang Rongsheng，Wu Hanguang)．消谐法SHEPWM的谐波影响数值分析(Numerical analysis of harmonic influence for selected harmonic elimination PWM)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2011，26(9):183-189．

［8］Sidney R Bowes，Paul R Clark．Regular-sampled harmonic-elimination PWM control of inverter drives［J］．IEEE Transactions on Power Electronics，1995，10(5):521-531．