大型直缝焊管压力矫直载荷修正系数优化
2014-06-24宋晓抗
宋晓抗,赵 军
(先进锻压成形技术与科学教育部重点实验室(燕山大学),066004秦皇岛河北)
大型直缝焊管压力矫直载荷修正系数优化
宋晓抗,赵 军
(先进锻压成形技术与科学教育部重点实验室(燕山大学),066004秦皇岛河北)
依据多次三点弯曲压力矫直控制策略,分别给出了基于最小二乘曲线拟合原理和基于弯曲变形能相等原理的最优载荷修正系数的确定方法.由有限元仿真结果可知,前者计算出的最优载荷修正系数偏大,这是由于忽略了当加载弯矩大于理论矫直弯矩时对管件的影响远大于加载弯矩未达到理论矫直弯矩时的影响,而包含该因素影响的基于弯曲变形能相等原理计算出的最优载荷系数则比较适用.不同几何尺寸、不同初始挠度分布、不同矫直次数的小尺寸管坯矫直的物理模拟实验结果验证了基于弯曲变形能相等原理计算最优载荷修正系数的可行性与可靠性,可将初始直线度为4‰~10‰的管件矫正到1.1‰以内.这为多次三点弯曲压力矫直控制策略提供了便捷途径,也为自动化和智能化矫直奠定了基础.
压力矫直;三点弯曲;载荷修正系数;弯曲变形能
大型直缝焊管作为油气管道采用的主要管型,国际上主要有UOE和JCOE/JCO两种成形方式.在生产过程中,受到焊接热应力、成形设备及模具整体直线度等因素的影响,时常导致最终成形的焊管的整体直线度不满足要求,需对其进行矫直.由于大型直缝焊管的几何特殊性,目前生产厂家多采用压力矫直的方法修正其直线度.
长期以来,大型直缝焊管压力矫直工艺的实施多由操作者凭经验和估计确定矫直行程,反复测量和试校.近年来国内外有很多学者对压力矫直工艺进行了研究,Katoh等[1]建立了单次压力矫直时三点弯曲过程中载荷-挠度关系,通过预测回弹量达到矫直控制的目的;Kim等[2]通过在线识别材料性能参数模块和模糊自学习系统实现了对齿条的自动矫直;崔甫等[3-5]从弹塑性理论出发对矫直的反弯过程进行了力学分析,建立了矫直曲率方程式,进而计算出最大挠度处的矫直行程;翟华[6]利用矫直曲率关系和修正Ramberg⁃Osgood弹塑性方程计算出单次矫直时所需的行程;凌鹤等[7]基于载荷-挠度关系提出了更为精确的行程-挠度模型,但该方法需要大量的实验数据才能拟合出其具体的表达式.不论是现行的生产应用还是大多数的理论分析,均只针对于将最大挠度处矫直,每次矫直前均需要测量整体的挠度分布,从而确定支点、压点位置、矫直行程等工艺参数,矫直效率极低,不易满足生产需求.
赵军等[8]给出了只需测量管件初始挠度1次,即可制定出相应的多次三点弯曲矫直工艺参数的方法.依据该方法随着矫直次数的增多,其矫直效果越好.为达到提高矫直效率,且保证矫直精度的目标,提出了载荷修正系数的概念,并采用有限元模拟的方法讨论了修正系数的取值.但该方法需要反复多次模拟矫直过程,不适合在线应用,故本文拟对多次压力矫直时最优修正系数的定量化方法展开研究,为实现定量化矫直和智能化矫直奠定理论基础.
1 理论基础
1.1 多次压力矫直控制策略
由文献[8]可知,大型直缝焊管的理论矫直弯矩是1条曲线.在实际生产中,多采用专用设备对大型直缝焊管进行矫直.该设备的两支点对称分布于压头两侧,每次压力矫直的实质为对称式三点弯曲,多次压力矫直时影响管件最终矫直效果的弯矩为锯齿形折线,结合上述分析,提出多次压力矫直控制策略,即当获得管件理论矫直弯矩后用锯齿形的折线去逼近该曲线.如图1所示,该锯齿形弯矩与理论弯矩的交点的χ坐标为各次压力矫直时的压点位置,锯齿形折线的延长线与χ轴的交点为其相应的左、右支点,即制定出了三点弯曲多次矫直的控制策略.
1.2 载荷修正系数
由图1可知,只有当矫直次数趋于无限多次时,其实际加载的锯齿形折线弯矩的矫直效果才能与理论矫直弯矩相当,即能够将待矫管件完全矫直.但在实际生产中为提高矫直效率,则需减少矫直次数.为达到提高矫直效率同时又保证矫直精度的目标,采用较少的矫直次数去获得与理论弯矩相当的矫直效果,就必须对锯齿形弯矩分布加以修正.为此引入一个宏观载荷修正系数λ,显然其值大于1.第i次矫直时压点处的修正后弯矩Mi′与理论弯矩Mi的关系为
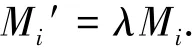

图1 多次压力矫直控制策略
若待矫管件的理论弯矩分布为M(χ),则其修正后的实际加载弯矩分布为M′(χ,λ),如图2所示.M′(χ,λ)的数学表达式为
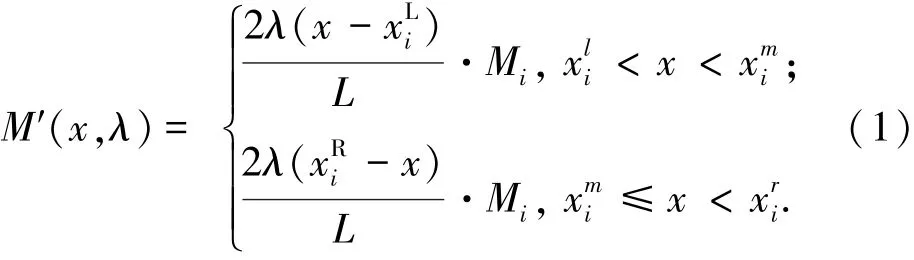
其中
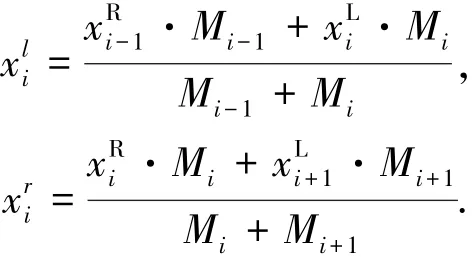
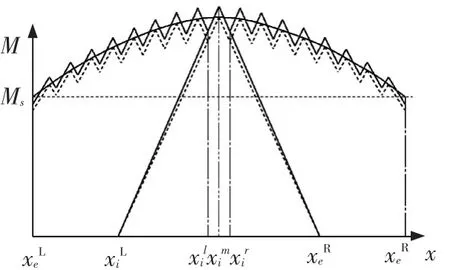
图2 修正后矫直弯矩
2 基于最小二乘曲线拟合的优化方法
由于多次压力矫直控制策略的实质为用多次压力矫直时影响管件最终矫直效果的锯齿形的折线弯矩去逼近管件理论矫直弯矩的光滑曲线,那么最优载荷修正系数应为使锯齿形折线最逼近理论曲线时所对应的载荷修正系数.数学上针对这类问题最常用的为最小二乘法.将该原理应用于求解最优载荷修正系数中,即为已知理论矫直弯矩分布[χ,M(χ)],欲求1条最佳的锯齿形折线,使∇最小,∇的表达式如下

以文献[8]中的大型管件为例,采用黄金分割法对式(1)中λ进行优化,结果如表1所示.由文献[8]中的有限元模拟结果可知,表1结果所显示出的趋势与有限元模拟结果相同,即随着矫直次数的增多,最优载荷修正系数下降.但表1所示的载荷修正系数远大于有限元模拟结果中将管件矫正到标准要求以内时所需的修正系数,即若采用表1所示的修正系数,待矫管件将被反弯过去且超出了矫直标准要求,故基于最小二乘曲线拟合计算的最优载荷修正系数偏大.

表1 基于最小二乘曲线拟合的最优载荷修正系数
3 基于弯曲变形能相等的优化方法
由文献[9]可知,管件压力矫直过程实质为平面曲梁的反向纯弯曲过程,基于文献[8-9]所述的理论可知,初始曲率为K0的曲管微段在弯矩M作用下发生反向纯弯曲变形时,弯矩M与反弯后曲率K在弹性和弹塑性变形阶段时的关系为
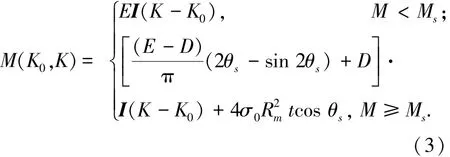
其中

式中:E为弹性模量;D为塑性切线模量;σs为材料初始屈服应力;σ0=σs(1-(D/E))称为截距应力;εs=σs/E为弹性极限应变;Rm为管件中径;t为管件壁厚;I=πR3mt为薄壁管坯截面惯性矩;Ms=(σs·I)/Rm为弹性极限弯矩.
由式(3)计算可得,M-K关系曲线如图3所示.而曲线下的面积就是初始曲率为K0曲管微段在弯矩M作用下发生弹塑性变形时产生的弯曲变形能.由图3可知,初始曲率为K0(χ)管件微段在理论矫直弯矩M(χ)的作用下发生弹塑性变形时的弯曲变形能为图3中ADE区域;但若实际加载的弯矩为(M+ΔM),则其弯曲变形能与理论弯矩时的差值为DEFG区域面积;若实际加载的弯矩为(M-ΔM),则其弯曲变形能与理论弯矩时的差值为BCDE区域面积.由图3可以看出DEFG>BCDE,说明这两种情况中,虽然实际加载弯矩与理论矫直弯矩之差的绝对值相等均为ΔM,但其弯曲变形能却相差很多.即基于最小二乘曲线拟合求解最优修正系数时,由于认为这两者对管件产生的影响是相当的,忽略了当加载弯矩大于理论弯矩时对管件的影响远大于加载弯矩未达到理论弯矩时的影响,使得最终计算出的载荷修正系数偏大.
依据上述讨论,提出基于弯曲变形能相等的载荷修正系数优化方法.设待矫管件在理论矫直弯矩M(χ)作用下的弯曲变形能为Utr,管件在实际加载弯矩M′(χ,λ)作用下的变形能为Ueq.定义这两者之差的绝对值U最小时的载荷修正系数为最优值,则由式(1)和式(3)可得U的表达式为
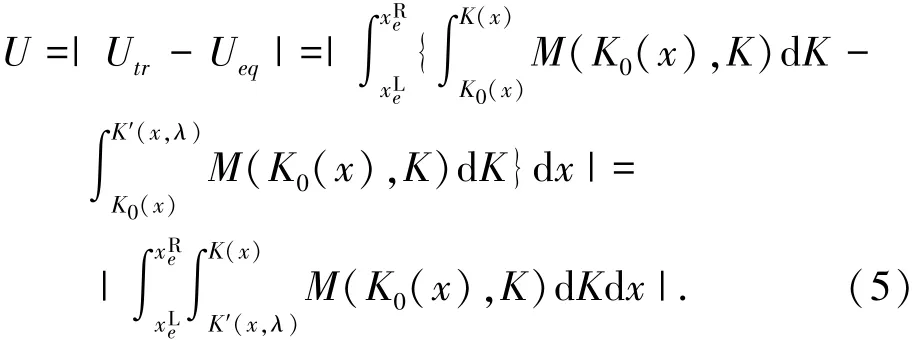
同样以文献[8]中的大型管件为例,其初始最大挠度为70.89 mm,即初始直线度为5.8‰.基于弯曲变形能相等对其载荷修正系数进行优化,式(5)的优化仍采用黄金分割法,结果如表2所示.由文献[8]中的有限元模拟结果可知,当矫直次数为3、4、5时,依据表2所示的修正系数对管件进行矫直,最终管件的最大残余挠度分别为-17.12、2.38、7.79 mm,即矫正后的直线度分别为1.4‰、0.19‰、0.64‰,满足了API Spec 5L行业标准中直线度2‰以内的要求[10].故基于弯曲变形能相等计算的最优载荷修正系数适用于大型管件的矫直.

表2 基于弯曲变形能相等的最优载荷修正系数
4 实验验证
分别对初始挠度不同、管件几何尺寸不同、矫直次数不同的小尺寸管坯进行基于弯曲变形能相等的最优载荷修正系数的验证实验,小尺寸管坯的材料和几何尺寸如表3所示.验证实验分为:1)相同初始挠度且同尺寸同材质的管坯,采用不同矫直次数时的验证实验;2)采用两种不同尺寸的管坯,分别对其初始挠度分布不同但相同矫直次数时的情况进行验证.
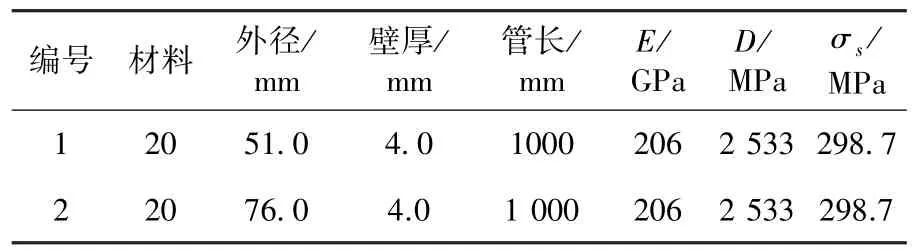
表3 管坯材料及几何尺寸
4.1 制备待矫管件
采用WDD-LCT-150型电子拉扭组合多功能试验机作为弯曲设备,挠度分布的测量采用便携式三坐标测量仪来完成.为制备曲率光滑、变形区域较大的小曲率曲管,采用四点弯曲的方式压制直管,实验模具如图4所示,模具的上模施力点间的距离和下模支点间的距离均可以根据需要进行调节.本实验中上模间距为320 mm,下模支点距离为900 mm,采用不同的上模压下量制备不同初始挠度分布的小曲率曲管,且为消除制备的小曲率曲管的残余应力及加工硬化对后续多次压力矫直工艺的影响,压制弹复后将这批管件进行了退火处理,实验参数及实验结果如表4所示.

图4 四点弯曲实验模具

表4 制备小曲率曲管mm
4.2 矫直实验
矫直实验中依旧采用WDD-LCT-150型电子拉扭组合多功能试验机作为矫直设备,所用矫直装置与工厂实际相似,即矫直设备的压点及两支点均固定位置,管坯移动实现多次矫直.两支点对称分布于压点两侧,其间距为L=600 mm,如图5所示.

图5 矫直实验模具
实验中均依据三点弯曲压力矫直控制策略对这8根管件进行矫直,实验流程为:
1)采用三坐标测量仪测量每根管坯的初始挠度分布,进行曲线拟合,获得其初始曲率分布;
2)计算出其相应的理论矫直弯矩分布;
3)依据文献[8]所述多次压力矫直时工艺参数的制定方法及本文所述的最优载荷修正系数确定方法,分别给出其相应的矫直控制策略.
4.2.1 初始挠度相近矫直次数不同的实验结果
由表4可知,管坯编号为11~13的待矫管坯,采用了相同的四点弯曲参数压制得到,由于各管坯材料性能参数的波动,其弹复后及退火后的挠度分布略有不同,但认为这3根管件的初始挠度相近.分别采用3、4、5次矫直控制策略对这3根管件进行矫直,控制参数及实验结果如表5所示.由表5可知,当初始挠度相近而矫直次数不同时,依据弯曲变形能相等计算出的最优载荷修正系数,可将初始直线度为5‰~6‰的管坯的直线度矫正到1‰以内,矫直效果较优,满足标准要求.
4.2.2 初始挠度不同矫直次数相同的实验结果
采用两种不同几何尺寸的管坯,分别对初始挠度分布不同但矫直次数相同的情况进行了实验验证,其中Φ76×4 mm的管坯依据4次压力矫直控制策略进行实验的控制参数及实验结果如表6所示;Φ51×4 mm的管坯亦采用了4次压力矫直控制策略,其控制参数及实验结果如表7所示.由表6、7可知,当采用相同的矫直次数对不同初始挠度、不同几何尺寸的管坯进行矫直时,依据弯曲变形能相等计算出的最优载荷修正系数,可将初始直线度为4‰~10‰的管坯的直线度矫正到1.1‰以内,矫直效果稳定.

表5 编号11~13管坯的矫直控制参数和实验结果

表6 Φ76×4 mm管件的矫直控制参数和实验结果

表7 Φ51×4 mm管件的矫直控制参数和实验结果
5 结 论
1)在多次三点弯曲压力矫直控制策略的基础上,分别给出了基于最小二乘曲线拟合和弯曲变形能相等的最优载荷修正系数的确定方法,为多次三点弯曲压力矫直控制策略的最终定量化实施提供了便捷途径.
2)大型管件的有限元仿真结果表明,基于最小二乘曲线拟合的最优载荷修正系数偏大,这是由于忽略了当加载弯矩大于理论弯矩时对管件的影响远大于加载弯矩未达到理论弯矩时的影响,而包含该因素影响的基于弯曲变形能相等的最优载荷系数则比较适用.
3)不同几何尺寸、不同初始挠度分布、不同矫直次数的小尺寸管坯矫直的实验结果验证了基于弯曲变形能相等的载荷修正系数优化方法的可行性与可靠性,经3~5次矫直便可将初始直线度为4‰~10‰的管件矫正到1.1‰以内,不仅能够保证矫直精度,而且可以大幅度提高矫直效率.
[1]KATOH T,URATA E.Measurement and control of a straightening process for seamless pipes[J].Journal of Engineering for Industry,1993,115(3):347-351.
[2]KIM Seung⁃cheol,CHUNG Sung⁃chong.Synthesis of the multi⁃step straightness control system for shaft straightening processes[J].Mechatronics,2002,12(1):139-156.
[3]崔甫.矫直理论与参数[M].北京:冶金工业出版社,1994.
[4]钦明浩,柯尊忠,张向军,等.精密矫直机中轴类零件矫直工艺理论研究[J].机械工程学报,1997,33(2):48-53.
[5]钦明浩,张向军,蒋守仁,等.轴类零件校直理论分析[J].合肥工业大学学报(自然科学版),1996,19(4):22-28.
[6]ZHAI Hua.Research on straightening technology cam system[J].Chinese Journal of Mechanical Engineering,2003,16(2):175-177.
[7]LU Hong,LING He,LEOPOLD J,et al.Improvement on the straightness of metal bar based on straightening stroke⁃deflection model[J].Science in China Series E:Technological Science,2009,52(7):1866-1873.
[8]赵军,宋晓抗,曹宏强,等.大型直缝焊管多次三点弯曲压力矫直控制策略[J].哈尔滨工业大学学报,2014,46(1):90-96.
[9]赵军,曹宏强,展培培,等.纯弯曲过弯矫直等价原理及其试验验证[J].机械工程学报,2012,48(8):28-33.
[10]ANSI/API Specification 5L.ISO 3183:2007,Specification for line pipe[S].Washington DC:API Publishing Service,2009.
(编辑 张 红)
Optimization research on load correction coefficient in process of press straightening for LSAW pipes
SONG Xiaokang,ZHAO Jun
(Ministry of Education Key Laboratory of Advanced Forging&Stamping Technology and Science(Yanshan University),066004 Qinhuangdao,Heibei,China)
To optimize load correction coefficient,based on press straightening control strategy with multi⁃step three⁃point bending process,two methods of least squares curve fitting and equivalent bending deformation energy were proposed.The simulation results of the Longitudinally Submerged Arc Welding(LSAW)pipe show that the optimum load correction coefficient calculated by least squares curve fitting method is bigger than normal.This is due to that,when the actual loading moment is greater than the theoretical straightening moment,the impact on the pipes is greater.However,the optimum load correction coefficient calculated by the equivalent bending deformation energy method,is more applicable,which is verified by the straightening physical simulation experiments of small sized pipes with different geometries,initial deflection distribution and straightening step.The straightness of the pipes with their initial straightness of 4‰~10‰can be improved within 1.1‰.Thus,this method provides a convenient way to carry out the press straightening control strategy with multi⁃step three⁃point bending process.
press straightening;three⁃point bending;load correction coefficient;bending deformation energy
TG306
:A
:0367-6234(2014)11-0090-05
2014-01-08.
国家自然科学基金(51175452).
宋晓抗(1987—),女,博士研究生;赵 军(1957—),男,教授,博士生导师.
赵 军,zhaojun@ysu.edu.cn.
