PIE+MOM的Mamdani模糊系统通用逼近性充要条件

游文虎，王 茂，施 佳

(1.哈尔滨工业大学空间控制与惯性技术研究中心，150001哈尔滨;2.中国航空无线电电子研究所，200241上海)

学者 Kosko［1］和 Wang［2］在 1992 年的 IEEE 模糊系统会议上提出了模糊系统可以作为通用逼近器，并分别从不同角度给予了证明.自此，不少学者围绕模糊系统作为通用逼近器开展了相关研究.Bova等［3］研究了Mamdani模糊系统的一种模糊逻辑推理过程.Wang等［4］分析了简化结构演变的Mamdani模糊系统辨识及其应用高维问题的方法.关于模糊系统作为通用逼近器的理论研究可分为3大类:存在性，充分性和必要性.

1)模糊系统通用逼近性的存在性.Kosko［1］首先建立加型模糊系统模型，然后采用有限覆盖定理对基于此模型的模糊系统的通用逼近性的存在性给出了分析;进一步和Dickerson等［5］共同分析了具备椭圆规则的加型模糊系统的通用逼近性.Buckley等［6］选取一类模糊控制器的传递函数作为研究对象，从泛函角度对模糊系统具有通用逼近性给出了存在性证明.Zeng等［7-8］分析研究了采用乘积和最小推理方法得到的模糊系统，得出了其具有通用逼近性的对给定输入的局部逼近特性的一般表达式，并给出了如何提高全局通用逼近性的方向性建议.Kóczy等［9］从“猫和鼠”等问题出发对采用最大-最小算子推理的Mamdani模型和T-S模型模糊系统的通用逼近性的存在性进行了研究.Cao等［10-11］从动态模型角度分别研究了T-S模糊模型和Mamdani模糊模型的通用逼近性.Cuong等［12］引入Mamdani模糊系统的一类分段多线性模型，并研究了其逼近能力.

2)模糊系统通用逼近性的充分性.Ying［13-14］采用构造性方法，分别分析了预先给定的逼近精度的T-S型和Mamdani型模糊系统作为通用逼近器的充分条件.Zeng等［15］通过对线性T-S性模糊系统的隶属函数作了一定的限制后给出了新的通用逼近性的充分性条件.黄卫华等［16］推导了输入采用广义线性隶属函数的典型Mamdani模糊系统的解析结构，并证明了通用逼近性.

3)模糊系统通用逼近性的必要性.Ying等［17-18］深入研究了一般单输入单输出、多输入单输出的Mamdani型模糊系统和典型的T-S型模糊系统可以作为通用逼近器的必要条件，并分析了其极可能具有最简洁系统构成.孙富春等［19］研究了单输入单输出(SISO)Mamdani模糊系统在给定逼近精度下作为函数逼近器的必要条件，对文献［17-18］的结论做了推广.

以上这些研究都没有给出某种情形下的模糊系统具有通用逼近性的充要条件.这些研究都是指针对某一特定类模糊系统的通用逼近能力，他们都未能解答具有通用逼近性能的模糊系统必须具备怎样的条件.具体采用怎样的途径和方法来构造模糊系统，从而使其具有通用逼近性，这仍然需要进一步的研究分析.

本文将分析并证明一类具有通用逼近性的Mamdani型模糊系统的充要条件.

1 一类通用逼近的Mamdani模糊系统

在研究模糊系统的逼近性能时，需要在有界闭区间上进行.因此，设定n维模糊系统的输入空间为［ai，bi］n，i=1，2，…，n.对区间［ai，bi］进行划分，即在区间［ai，bi］上定义Ni个模糊数，且有，则有，其中Cj i为Aj

i的中心点.

定义1 设T:［0，1］×［0，1］→［0，1］，T是T-norm，当且仅当对于所有的x，y，z∈［0，1］有:

1)T(x，y)=T(y，x)(交换律);

2)当y≤z，T(x，y)≤T(y，x)(单调性);

3)T(x，T(y，z))=T(T(x，y)，z)(结合律);

4)T(x，1)=x.

定义2 乘积推理机(PIE).指定U上的给定模糊集A'向V上的模糊集B'的映射规则如下:

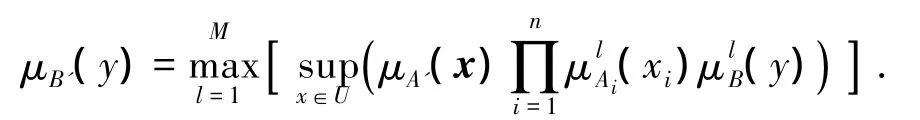
其中μA'(x)表示模糊集分别为模糊规则前件、后件的隶属度函数.

Mamdani模糊系统的结构比T-S模糊系统的结构要复杂得多，因为对于Mamdani模糊系统来说，其规则后件也为模糊数，而且解模糊器也有多种选择.本文只讨论基于乘积推理机(PIE)的情形.

对于Mamdani型模糊系统，根据其规则后件的不同，其模糊系统具有不同形式.当采用一般解模糊化算子［20］时，其模糊系统具有如下形式:

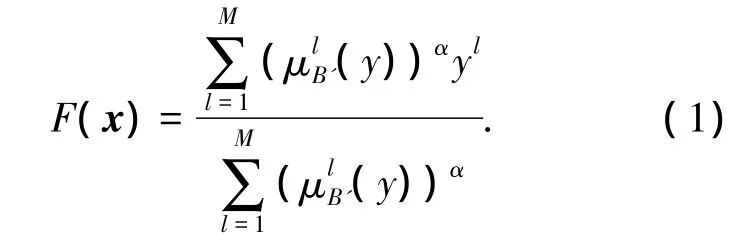
其中:M为该模糊系统的模糊规则数;yl为)取最大值时所对应的点;)α表示第l个模糊规则的合成算子，且

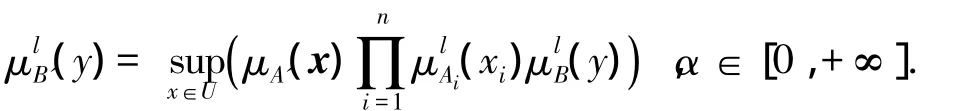
当取α=1时，表示上式采用面积平均解模糊器，取α=+∞时，则采用了最大值平均解模糊器(MOM).

引理1(Weierstrass第一定理)［21］设f(x)是在区间［a，b］上定义的连续函数，则任意给定ε＞0，都存在多项式P(x)，使得

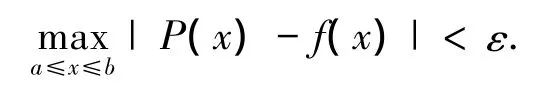
如下定理将给出一类Mamdani型模糊系统是否具有通用逼近性的结论.

定理1 给定一个在定义域D上的任意连续函数f(x)和任意的逼近精度ε＞0时，若模糊系统F(x)的推理机为乘积推理机，且解模糊器为最大值平均解模糊器，则 Mamdani模糊系统F(x)具有通用逼近性的充要条件:

也就是说，当符合上述条件的Mamdani模糊系统F(x)满足下式:

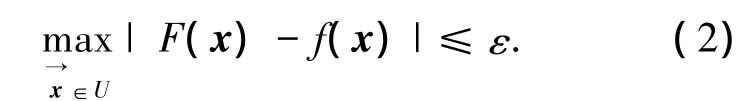
证明 对于式(1)对应的模糊系统的模糊规则后件有两种选择方式.

1)规则后件为单点规则后件，即

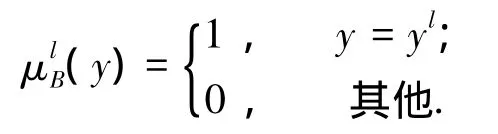
在这种情形下，由于μAi(xi)＞ξ(其中ξ为一足够小的正常数)，所以一定存在τ=τ(ξ)＞0，使得

在式(1)中，yl(l=1，2，…，M)为常数.不妨设和ya=，则中一定存在N个常值小于或等于ya，M-N个大于ya.不失一般性，设前N个常值小于或等于ya.

采用最大值平均解模糊器(MOM)，即α=+∞时，有

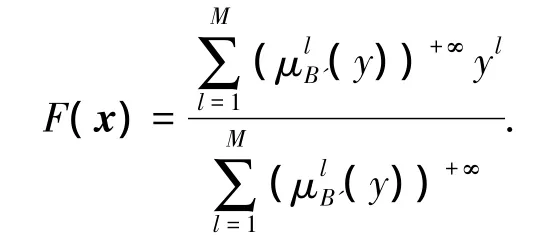
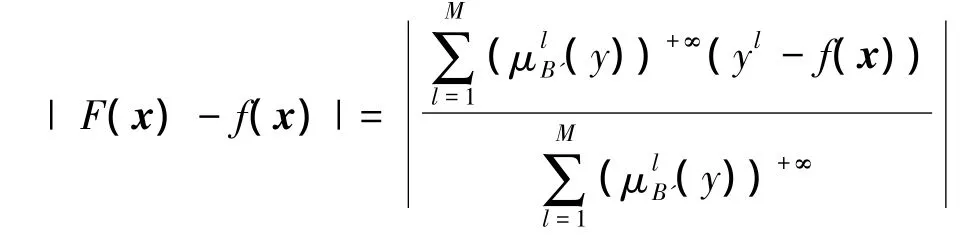
可推出

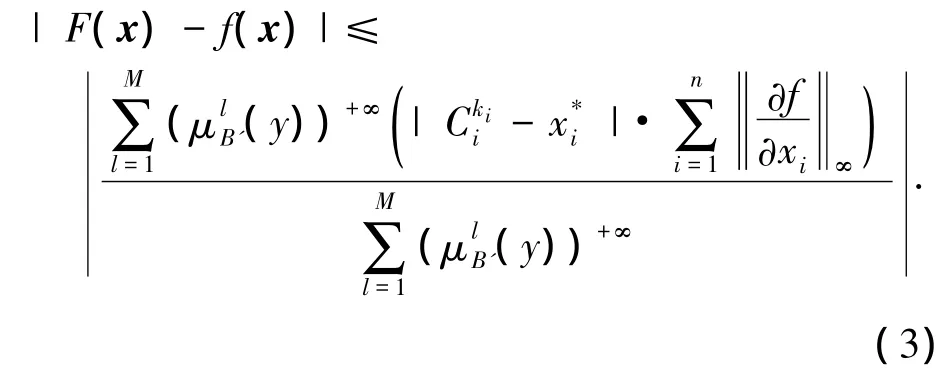
当对应的输入点x*的各个分量只有一个输入隶属函数值为最大，则式(3)可化为

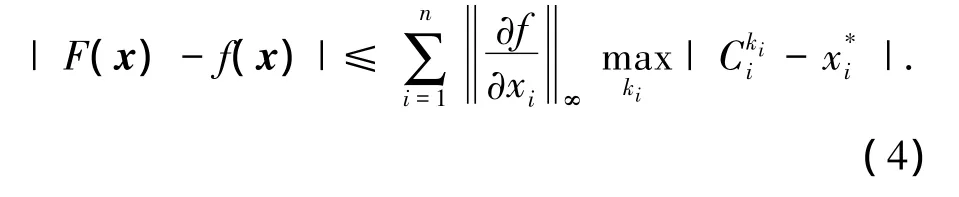
若对于该点有a个输入隶属函数值相等且为该点处最大的隶属值，则式(3)也可化为

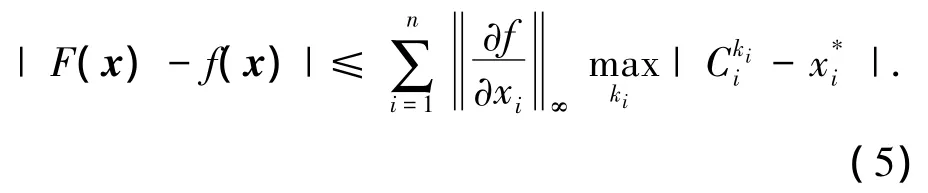
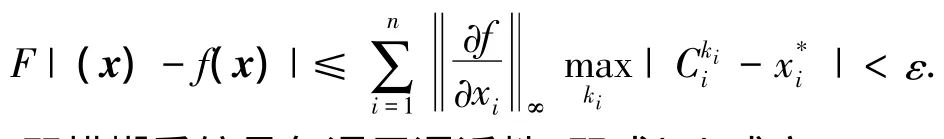
即模糊系统具备通用逼近性，即式(2)成立.

②必要性证明.采用反证法，假设系统不满足上述条件，而该模糊系统仍具有通用逼近性.

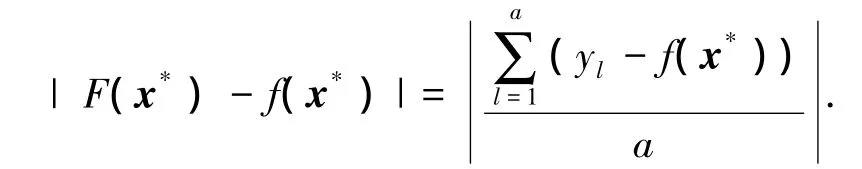
可得到

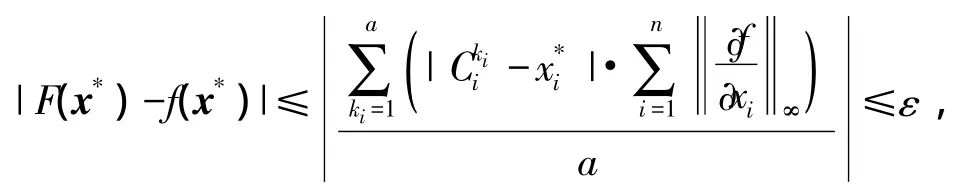
即对于给定的ε，在模糊规则数足够大时，由隶属函数满足的条件可知，一定存在

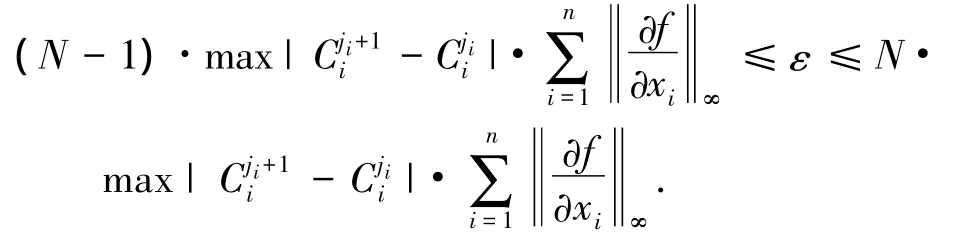
将上两式比较可得

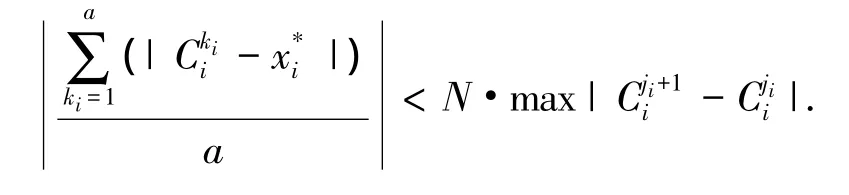
所以有

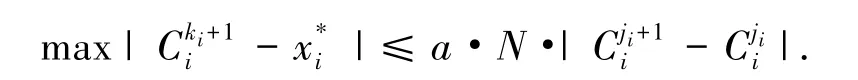
这与该情形不符，显然假设不成立.故这种情形下模糊系统不具有通用逼近性.

证毕.

2)规则后件为模糊数，即

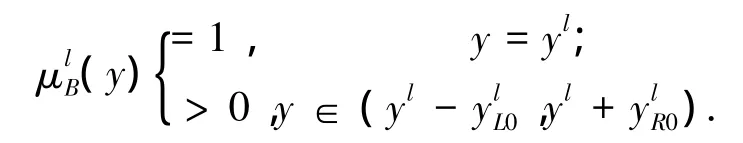
其中yl为模糊数的中心点，且)是凸函数.

在这种情形下，由于μAi(xi)＞ξ(ξ为一正常数)，所以采用模糊推理后，一定存在τ=τ(ξ)＞0，使得在区间中必有均为正的常数，且必有)在区间中为最大.

在式(1)中，yl(l=1，2，…，M)为常数.不妨设)和ya=，则yl(l=1，2，…，M)中一定存在N个常值小于或等于ya，M-N个大于ya.不失一般性，设前N个常值小于或等于N.

采用最大值平均解模糊器，即α=+∞ 时，在这种情形下，有

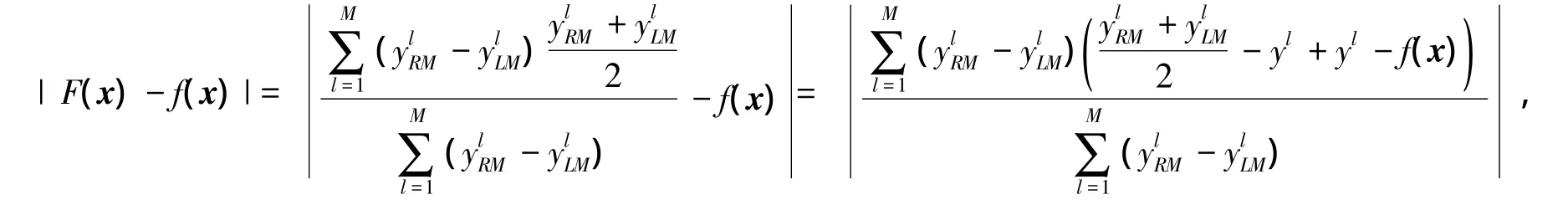
可得

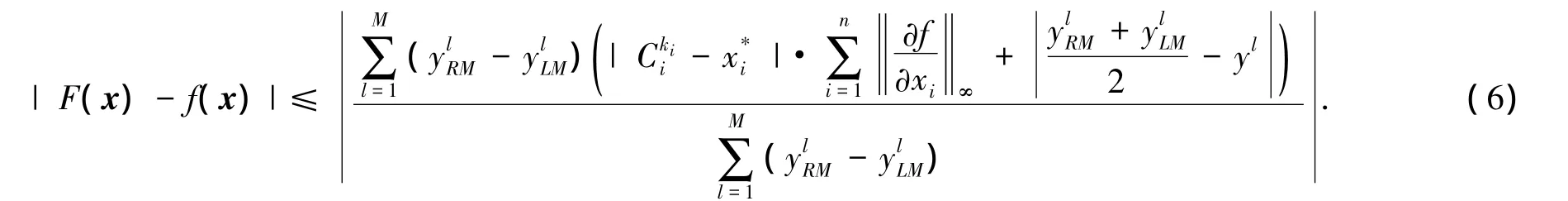
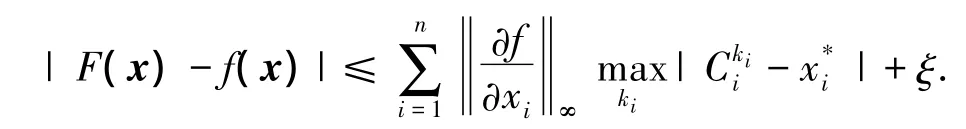
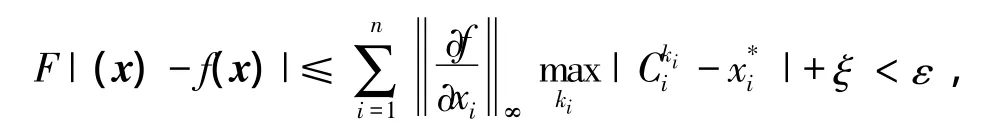
即模糊系统具备通用逼近性，即有式(2)成立.

②必要性证明.采用反证法，假设不满足条件时，该模糊系统仍具有通用逼近性.

这里有两种情形:

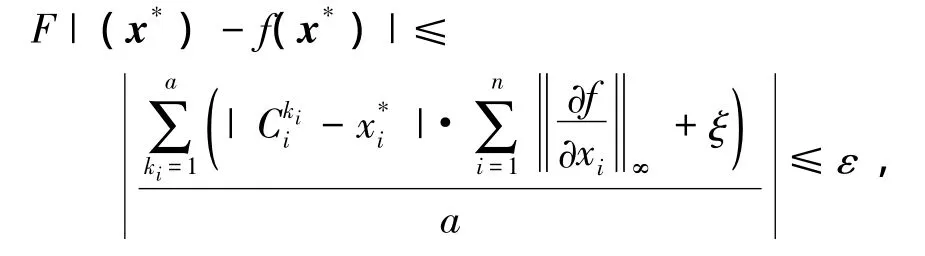
即对于给定的ε，在模糊规则数足够大时，一定存在

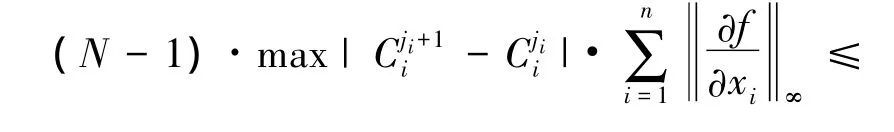
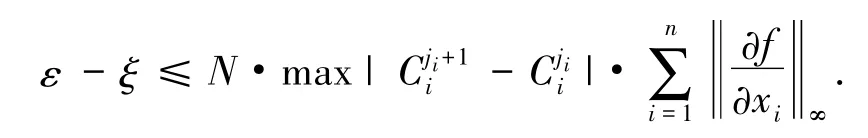
将上两式比较可得

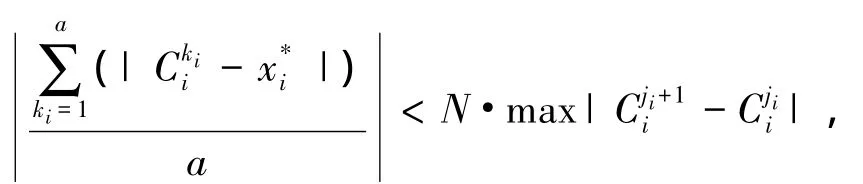
这与该情形不符，假设不成立.

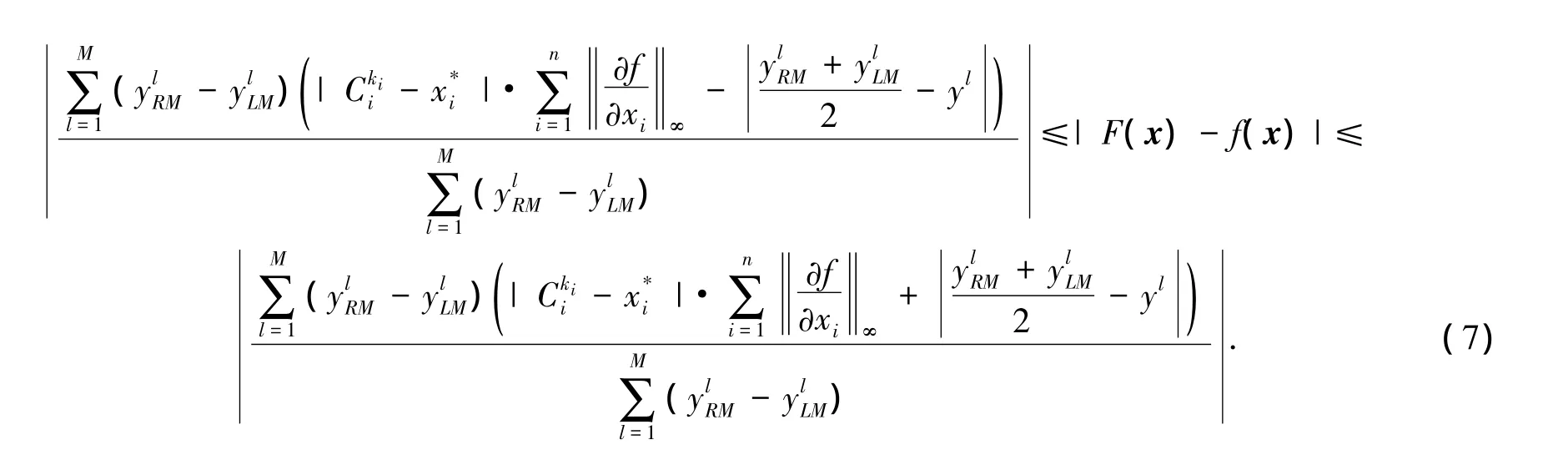
对于左边界点处有

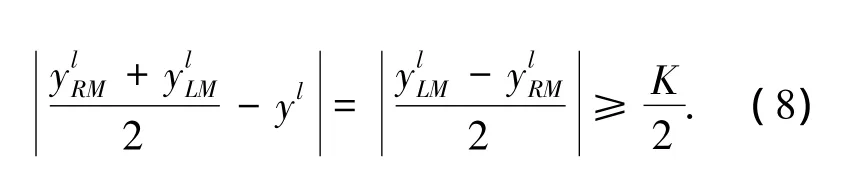
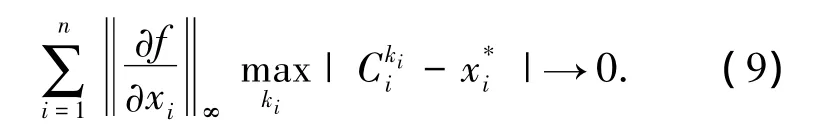
由式(7)～(9)可得

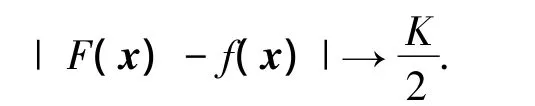
故在此情形下，假设不成立.

综上两种情形，不满足条件时，该Mamdani模糊系统不具有通用逼近性.

证毕.

2 Mamdani模糊系统通用逼近性判据分析

满足上述判据的Mamdani模糊系统在规则数足够多的情形下可以以任意精度逼近紧致集上的任意连续函数.若是不满足上述判据的话，无论规则数有多少总存在紧致集上的某一连续函数使得该模糊系统不能以任意精度逼近.下面构造不同的Mamdani模糊系统来逼近两个函数比较以确认上述判据的正确性.为了反映普遍性.在选取被逼近函数时选择指数函数和三角函数.因为指数函数的傅里叶展开式为无穷阶多项式，而多项式可以以任意精度逼近任意紧致集上的连续函数;再就是三角函数为周期函数也具有一定的代表性.下面针对本文所给判据作举例分析.

示例 现有在区间［0，1］上的两个函数g1(x)=ex和g2(x)=sin(2π·x)，分别构造满足解模糊器为最大值平均解模糊器时的判据的Mamdani模糊系统和不满足该判据的Mamdani模糊系统来逼近这两个函数.

由于条件限制推理机必须选取局域推理机.不失一般性，选择乘积推理机.隶属函数选择高斯型隶属函数exp(-((x-xl)/σl)2).

首先构造满足判据的Mamdani模糊系统.由该判据可知，当隶属函数是局域隶属函数时，满足判据，当隶属函数为全域隶属函数时，只要其满足一定的条件，依然满足判据.如当采用高斯型隶属函数时，其参数σl(l=1，2，…，n0)都为同一值.

分别给出规则数为21和51的满足上述判据的Mamdani模糊系统来逼近函数g1(x)=ex，σl=0.8(l=1，2，…，n0).Mamdani模糊系统输出和逼近误差分别如图1～2所示.

再给出规则数分别为21和51的满足该判据的Mamdani模糊系统来逼近函数g2(x)=sin(2π·x)，σl=0.8(l=1，2，…，n0).系统输出和逼近误差分别如图3～4所示.

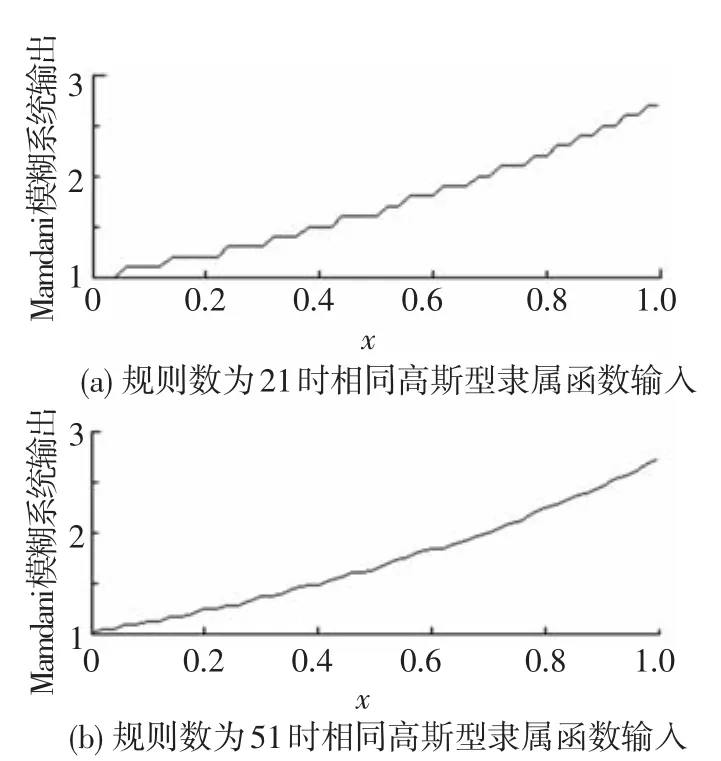
图1 满足判据的Mamdani模糊系统对g1(x)=ex的输出

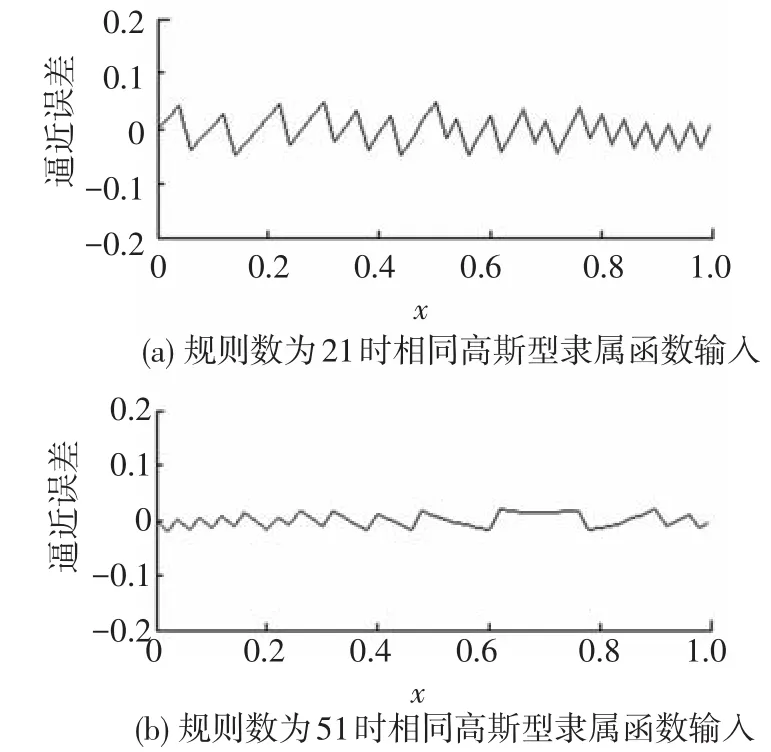
图2 满足判据的Mamdani模糊系统对g1(x)=ex的逼近误差

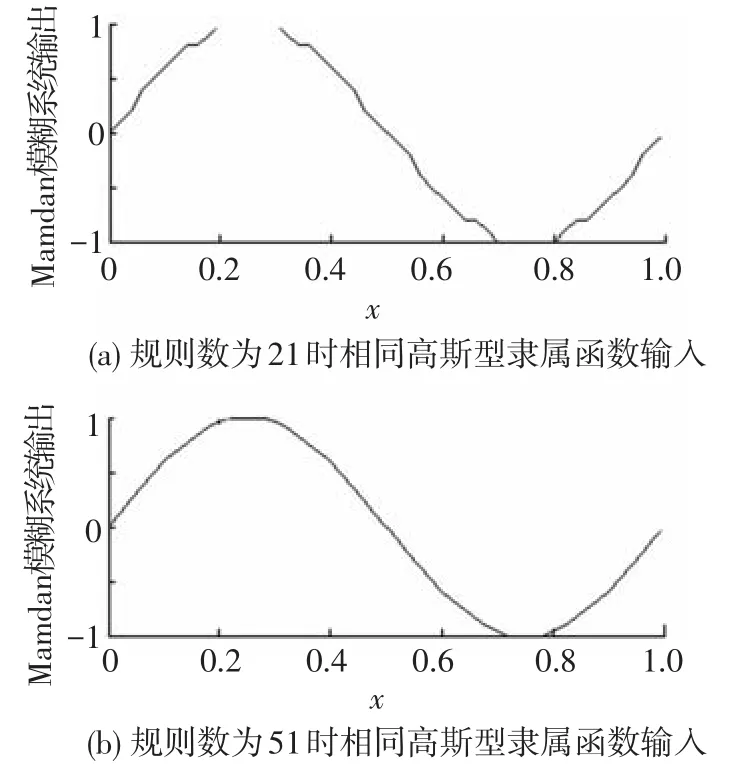
图3 满足判据的Mamdani模糊系统对g2(x)=sin(2π·x)的输出

下面构造不满足该判据的Mamdani模糊系统.选取第一个规则的规则前件的隶属函数为定值σ1=0.8，其他的分别为:当规则数为21时σl=0.025(l=2，3，…，n0);当规则数为 51 时σl=0.01(l=2，3，…，n0).首先给出其对g1(x)=ex的仿真图，系统输出如图5所示.

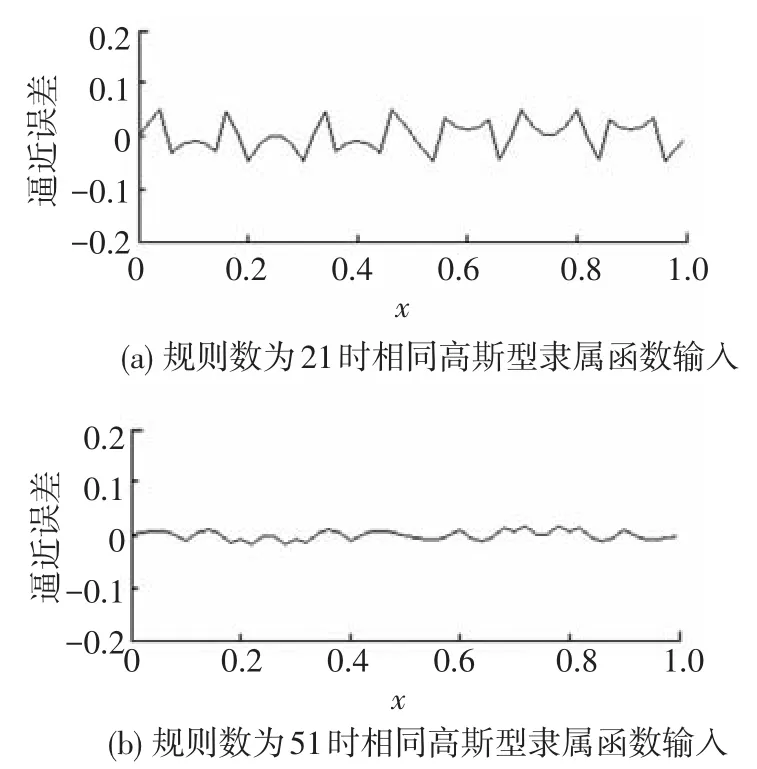
图4 满足判据的Mamdani模糊系统对g2(x)=sin(2π·x)的逼近误差

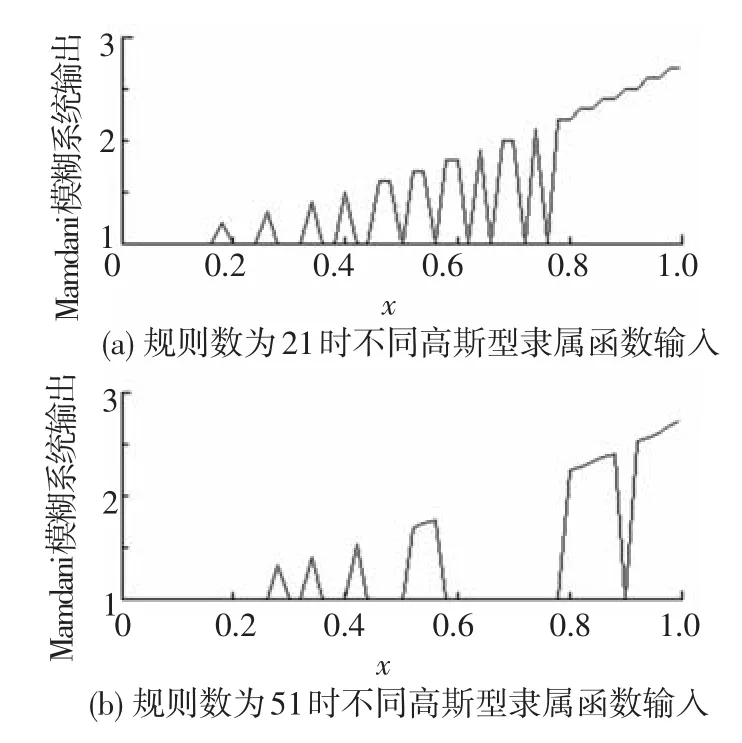
图5 不满足判据的Mamdani模糊系统对g1(x)=ex的输出

再给出其对g2(x)=sin(2π·x)的仿真图，系统输出如图6所示.

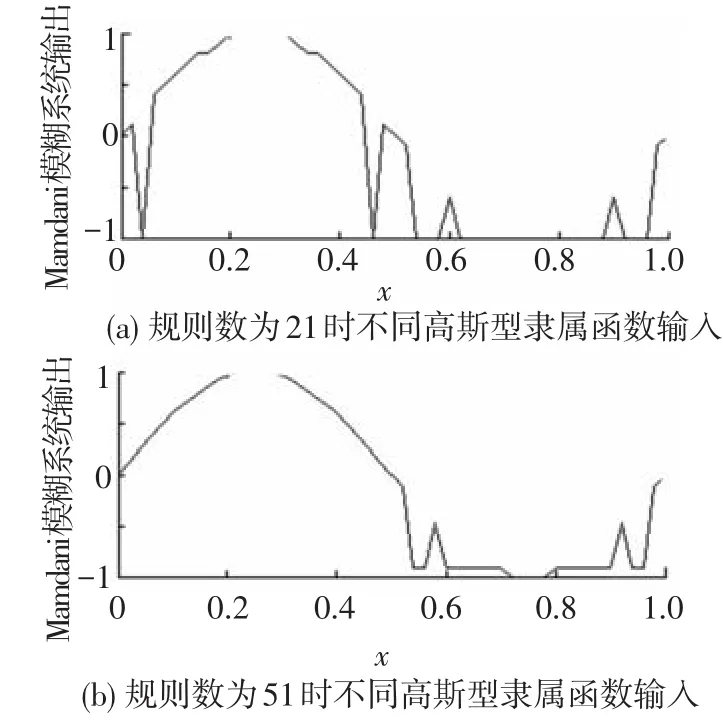
图6 不满足判据的Mamdani模糊系统对g2(x)〛=sin(2π·x)的输出

由此可得，在推理机为局域推理机的情形下，满足该判据的Mamdani模糊系统具有通用逼近性.不满足该判据且采用最大值平均解模糊器的Mamdani模糊系统不具有通用逼近性.

3 结语

本文率先给出了一类Mamdani模糊系统具有通用逼近性的充要条件.由上述定理证明结果可知，当解模糊器为最大值平均解模糊器时，Mamdani模糊系统的具有通用逼近性的充要条件是:模糊器和规则前件的隶属函数中所有满足的隶属函数的中心点，具有当一定有0的性质和规则后件的隶属函数具有如下性质，即当一定有使得其对应的规则后件隶属函数的隶属度的值的取值范围长度也趋近于零.

［1］ KOSKO B.Fuzzy systems as universal approximators［C］//1992 IEEE International Conference on Fuzzy Systems.San Diego:［s.n.］，1992:1153-1162.

［2］WAMG Lixin.Fuzzy systems are universal approximators［C］//1992 IEEE International Conference on Fuzzy Systems.San Diego:［s.n.］，1992:1163-1170.

［3］BOVA S，CODARA P，MACCARI D，et al.A logical analysis of Mamdani-type fuzzy inference，I theoretical bases［C］//Fuzzy Systems(FUZZ)，2010 IEEE International Conference on.Piscataway:IEEE，2010:1-8.

［4］ WANG D，ZENG X J，KEANE J A.A simplified structure evolving method for Mamdani fuzzy system identification and its application to high-dimensional problems［J］.Information Sciences，2013，220:110-123.

［5］ DICKERSON JA， KOSKO B. Fuzzyfunction approximation with ellipsoidal rules［J］. IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，1996，26(4):542-560.

［6］ BUCKLEY J J. Universalfuzzy controllers［J］.Automatica，1992，28(6):1245-1248.

［7］ZENG X J，SINGH M G.Approximation theory of fuzzy systems-MIMO case［J］.IEEE Transactions on Fuzzy Systems，1995，3(2):219-235.

［8］ZENG X J，SINGH M G.Approximation properties of fuzzy systems generated by the min inference［J］.IEEE Transactions on Systems，Man，and Cybernetics，1996，26(1):187-193.

［9］ KÓCZY L T， ZORAT A. Fuzzysystemsand approximation［J］.Fuzzy Sets and Systems，1997，85(2):203-222.

［10］CAO S G，REES N W，FENG G.Universal fuzzy controllers for a class of nonlinear systems［J］.Fuzzy Sets and Systems，2001，122(1):117-123.

［11］CAO S G，REES N W，FENG G.Mamdani-type fuzzy controllers are universal fuzzy controllers［J］.Fuzzy Sets and Systems，2001，123(3):359-367.

［12］CUONG B C，LONG H V.An approach to the functions approximation problemsby Mamdanifuzzysystem［C］//Control， Automation， Robotics and Vision，2008.ICARCV 2008.10th International Conference on.Piscataway:IEEE，2008:850-855.

［13］YING H.Sufficient conditions on general fuzzy systems as function approximators［J］.Automatica，1994，30(3):521-525.

［14］YING H.Sufficient conditions on uniform approximation of multivariate functions by general Takagi-Sugeno fuzzy systemswith linearrule consequent［J］.IEEE Transactions on Systems，Man and Cybernetics，1998，28(4):515-520.

［15］ZENG K，ZHANG N Y，XU W L.A comparative study on sufficient conditions for Takagi-Sugeno fuzzy systems as universal approximators［J］.IEEE Transactions on Fuzzy Systems，2000，8(6):773-780.

［16］黄卫华，方康玲，章政，等.具有广义线性隶属函数的典型模糊系统的通用逼近性［J］.计算机应用研究，2010，27(4):1263-1265，1269.

［17］YING H，DING Y，LI S，et al.Comparison of necessary conditions for typical Takagi-Sugeno and Mamdani fuzzy systems as universal approximators［J］.IEEE Transactions on Systems，Man and Cybernetics，1999，29(5):508-514.

［18］DING Y，YING H，SHAO S.Necessary conditions on minimal system configuration for general MISO Mamdani fuzzy systems as universal approximators［J］.IEEE Transactions on Systems，Man，and Cybernetics，2000，30(6):857-864.

［19］孙富春，杨晋，刘华平.SISO Mamdani模糊系统作为函数逼近器的必要条件［J］.智能系统学报，2009，4(4):288-294.

［20］ FILEV D P， YAGER R R. A generalized defuzzification method via BAD distributions［J］.International Journal of Intelligent Systems，1991，6(7):687-697.

［21］DAVIS P J.Interpolation and Approximation［M］.New York:Blaisdell Pub，1963.