Shearlet变换与核各向异性扩散的图像噪声抑制

吴一全，叶志龙，万 红，刚 铁

（1.南京航空航天大学电子信息工程学院，210016南京；2.先进焊接与连接国家重点实验室（哈尔滨工业大学），150001哈尔滨；3.深圳市城市轨道交通重点实验室（深圳大学），518060深圳）

Shearlet变换与核各向异性扩散的图像噪声抑制

吴一全1，2，3，叶志龙1，万 红1，刚 铁2

（1.南京航空航天大学电子信息工程学院，210016南京；2.先进焊接与连接国家重点实验室（哈尔滨工业大学），150001哈尔滨；3.深圳市城市轨道交通重点实验室（深圳大学），518060深圳）

为了更有效地抑制图像噪声，改善图像视觉效果，提出了一种基于非下采样Shearlet变换（nonsubsampled shear⁃let transform，NSST）与核各向异性扩散的图像噪声抑制方法.首先对含噪图像进行非下采样Shearlet变换；然后对所得到的低频和高频分量分别进行改进的全变差（improved total variation，ITV）扩散与核各向异性扩散（kernel anisotropic diffu⁃sion，KAD）；最后对扩散后的低频和高频分量进行非下采样Shearlet逆变换得到噪声抑制后的图像.给出了实验结果，并且依据主观视觉效果和峰值信噪比、结构相似度两种定量评价指标，与近年来提出的基于小波阈值收缩结合全变差、基于复Contourlet域非线性扩散、自适应Shearlet域约束的全变差等3种噪声抑制方法进行了比较.实验结果表明，该方法的噪声抑制能力更强，且更为完整地保留了图像的边缘和细节信息.

图像处理；噪声抑制；非下采样Shearlet变换；改进的全变差扩散；核各向异性扩散

由于外部条件和系统设备因素的影响，图像在形成和传输过程中常常会引入噪声，严重影响了图像的质量.在焊接缺陷、织物疵点、纸病和铁轨表面缺陷的自动检测中［1-2］，噪声抑制作为其图像预处理的重要环节，对于提升后续图像分析及识别的性能有着重要意义.目前，图像噪声抑制方法主要有滤波法和多尺度几何分析法.传统的滤波法包括中值滤波、邻域滤波、低通滤波等，这类方法虽可在一定程度上抑制噪声，但同时平滑了较多的图像细节信息.而滤波法中较为新颖的非局部均值方法［3-4］则充分利用图像的自相似性，通过衡量图像块的相似性来构造权重，能较好地保留图像边缘、纹理特征，但该方法的计算复杂度巨大，难以直接应用于实际场合.多尺度几何分析法以小波变换为基础［5］，可有效地表示图像的方向信息，在抑制噪声的同时保留图像的细节.近年来，各向异性扩散因其良好的细节保持特性在图像噪声抑制领域得到了广泛应用.以PM（perona malik）［6］、全变差（total variation，TV）［7］等为代表的各向异性扩散模型取得了较好的噪声抑制效果，但是这类方法未考虑图像噪声的分布情况，直接对图像进行全局化处理，易残留噪声，丢失细小边缘.而多尺度几何分析能够稀疏地表示图像［8-10］，可有效地分离图像的高、低频分量，并根据噪声的分布情况做相应的处理，改善噪声抑制效果.因此，若能充分利用多尺度几何分析和各向异性扩散的各自优势，可望达到更为优良的噪声抑制性能.文献［11］提出了基于小波阈值收缩结合TV的噪声抑制方法，较好地去除了噪声，但该方法采用的小波变换不能最优地表达图像，方向选择较为有限，且高频分量采用的阈值收缩方法也平滑了部分细节信息.文献［12］使用复Contourlet代替小波变换，并对高频分量进行PM扩散，有效地改善了噪声抑制效果.该方法采用的复Contourlet较小波虽能更稀疏地表示图像，对方向信息的表达也更加丰富，但方向的选择性仍受限于图像的分解尺度，且高频分量采用的PM扩散模型无法抵抗强噪声的攻击，应用范围受到了限制.近年来提出的Shearlet变换能够自适应跟踪图像奇异曲线方向，方向选择性更加丰富［13］，但Shearlet变换具有下采样操作，缺乏平移不变性.文献［14］给出了一种自适应Shearlet域约束的全变差图像噪声抑制方法，取得了较好的效果.然而该方法未对Shearlet变换后的低频分量进行处理，残留了部分噪声，且用于重构后图像处理的TV扩散在图像边缘和图像平滑区域均采用相同的方式进行扩散，易出现阶梯效应.针对上述问题，可考虑先采用非下采样Shearlet变换（NSST）将图像分解成高、低频分量，克服Shearlet产生的伪吉布斯（Gbbis）效应；对图像的低频分量，可在TV扩散的基础上，通过计算像素点的梯度值分辨图像的边缘区域和平滑区域，并采用不同的扩散策略，以改善图像视觉效果，提高扩散的效率［15］；此外，通过核化PM模型中的梯度算子，利用非线性函数将高频分量映射到高维特征空间，进行核各向异性扩散（KAD）处理，提升噪声的抑制性能，增强扩散的鲁棒性［16］.

基于上述分析，本文提出了一种基于NSST和核各向异性扩散的图像噪声抑制方法.首先对图像进行NSST，对得到的低频分量采用改进的TV扩散，改善视觉效果；然后高频分量则进行KAD扩散，以增强扩散的鲁棒性；最后利用非下采样Shearlet逆变换进行重构，得到噪声抑制后的图像.文中给出了实验结果，与基于小波阈值收缩结合TV的噪声抑制方法（WSTV）、基于复Contourlet域非线性扩散噪声抑制方法（CCPMTV）、自适应Shearlet域约束的全变差图像噪声抑制方法（SHTV）做了比较，并依据主观视觉效果及峰值信噪比（PSNR）、结构相似度（SSIM）等客观定量指标对上述方法进行了评价对比.

1 Shearlet变换

Shearlet变换克服了小波变换不能最优表示图像的缺点；且与Contourlet变换相比，剖分方向不受分解层数制约，可更为精确地表示图像的方向信息.在维数为2时，Shearlet函数的仿射系统为［17-18］

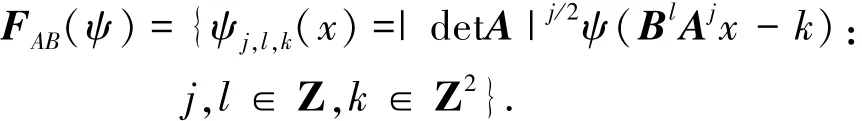
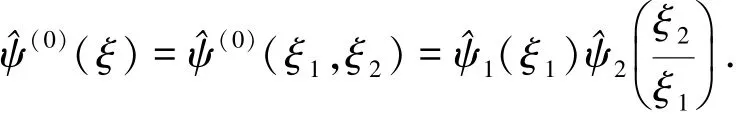
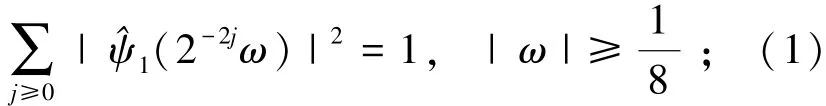
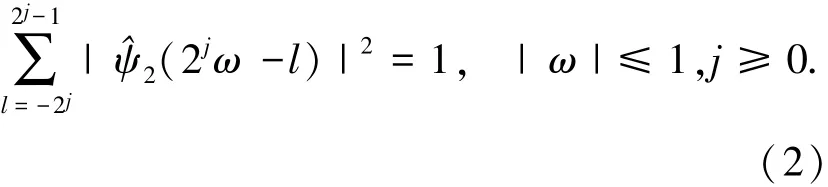
由式（1）和式（2）可知，对∀（ξ1，ξ2）∈D0，其中为水平锥，存在

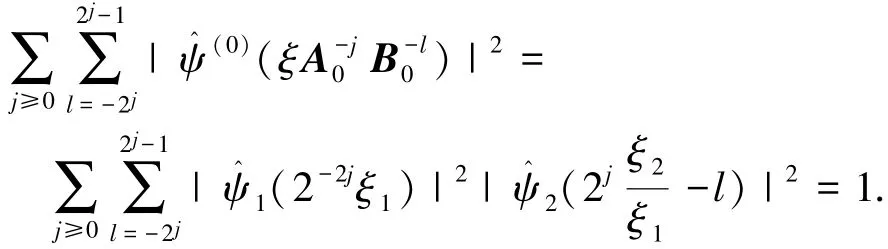
小波函数ψj，l，k具有如下频域支撑区间

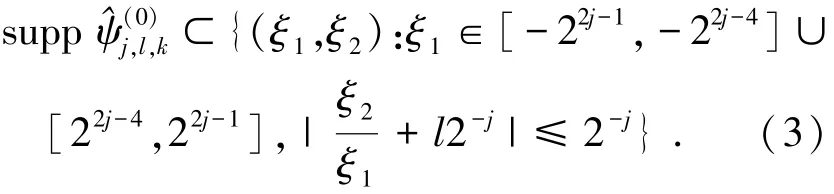
由式（3）可知，ψj，l，k支撑区域为一梯形对，其大小约为22j×2j，方向与斜率为l2-j直线方向一致，如图1（b）所示.从图1中可以看出Shearlet变换具有丰富的分解层数和分解方向，可以更为精确地表示图像信息.

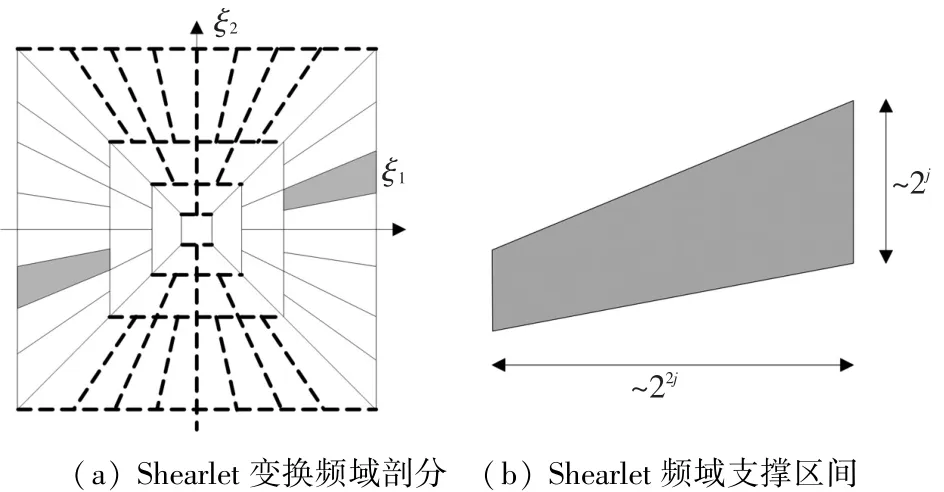
图1 Shearlet变换频域剖分及支撑区间示意

综上可知L2（D0）∨＝｛f∈L2（R2）：supp＾f⊂的一个Parseval框架为

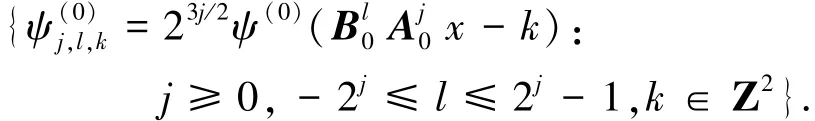
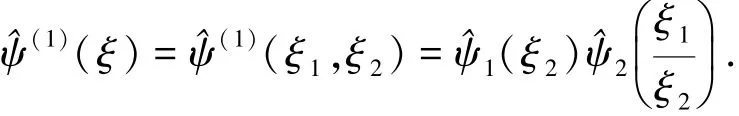
2 核各向异性扩散和改进的TV扩散

2.1 核各向异性扩散（KAD）

当图像遭受强噪声污染时，梯度算子无法分辨噪声引起的灰度变化与图像边缘引起的灰度变化.此时，若仍用梯度算子控制扩散过程，不仅不能有效抑制噪声，甚至会增强一部分噪声［14，19］.针对这一问题，可考虑进行核各向异性扩散（KAD）.根据模式可分性的Cover原理，核各向异性扩散算法通过非线性核函数将图像信息从原始图像空间映射到高维特征空间，利用特征空间中的梯度算子控制扩散过程，能够将噪声和图像边缘间的线性不可分问题转化为特征空间中的线性可分问题，从而更有效地抑制噪声.KAD的模型为

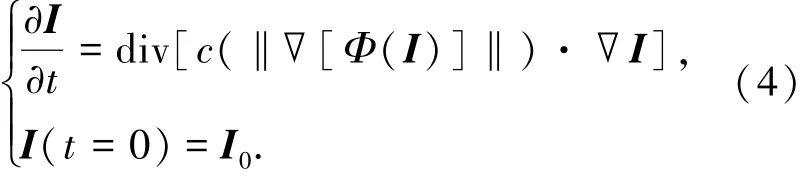
式中：div为散度算子；∇为梯度算子；‖·‖为幅度；I为含噪图像；I0为原始图像；t为时间算子，表示噪声抑制过程与扩散时间相关；‖∇［Φ（I）］‖为经函数Φ映射后特征空间中的梯度模，也称为核梯度模；c（‖∇［Φ（I）］‖）表示扩散方程，其形式为

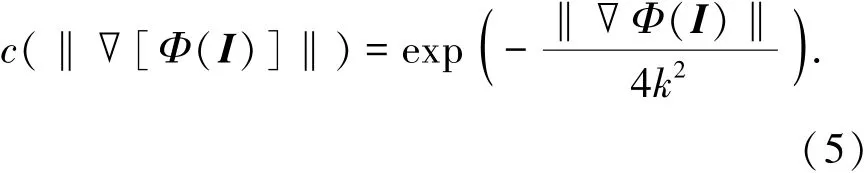
式中：k为扩散门限，且k＝1.482 6·［fmed·［｜‖∇［Φ（I）］‖-fmed（‖∇［Φ（I）］‖）｜］］，其中fmed为取中值函数［20］．

图像中某一像素点的梯度模可离散为某一特定方向上的灰度差分绝对值，因此，在图像空间像素点p处的梯度模‖∇Ip‖可以离散化为

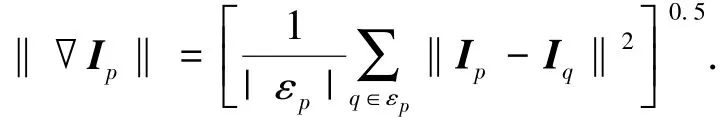
式中：εp为像素点p的8邻域空间；｜εp｜为εp的势．经过核替换后，特征空间中某一特定方向上的灰度差分平方为

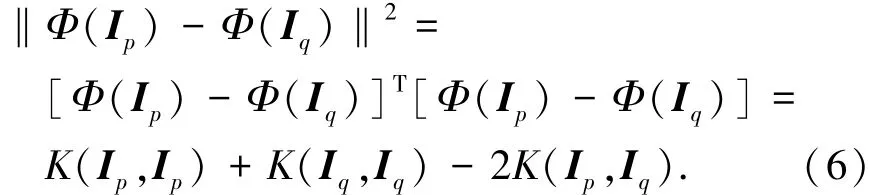
式中：K（·，·）为核函数，通常选取在特征空间能有效划分噪声和图像边缘的高斯函数，核梯度模为

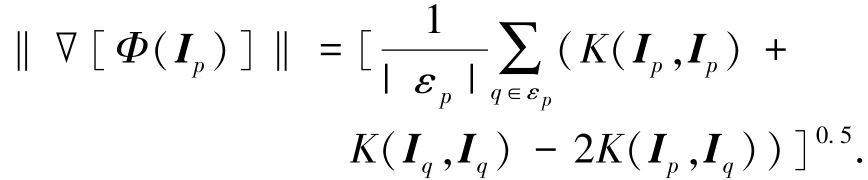
2.2 改进的TV（ITV）扩散

TV扩散可以归结为寻找图像能量泛函的平衡态，即求解方程最小化问题为

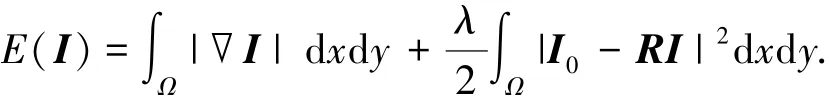
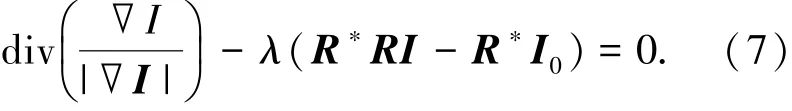
式中R∗是R的共轭伴随算子，式（7）的解I即为噪声抑制后的图像．

由式（7）可看出，由于TV扩散未根据图像特征的明显程度采用合适的扩散速度，其扩散效率较低；另外，TV扩散沿着边缘方向进行扩散，而在图像中较为平坦的区域，边缘事实上并不存在，此时仍然沿着边缘扩散，就会出现假边缘，产生“阶梯”效应、噪声抑制不完全等现象.因此，可对TV扩散进行如下改进［15］：

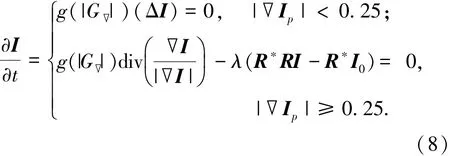
式中：g（｜G∇｜）用以加速迭代的速度，其中为图像中的点（χ，y）梯度向量的模．若在点（χ，y）的邻域内加权均值较小，则（χ，y）邻域内的像素变化平缓，扩散速度也就较快；反之，扩散速度就较慢．ITV扩散针对TV扩散模型的缺点进行相应的改进，因此较好地保留了图像边缘，使得图像平坦区域更为光滑，并提高了扩散效率．

3 图像噪声抑制方法的步骤与流程

本文提出一种有机结合NSST和核各向异性扩散的图像噪声抑制方法，其流程如图2所示.

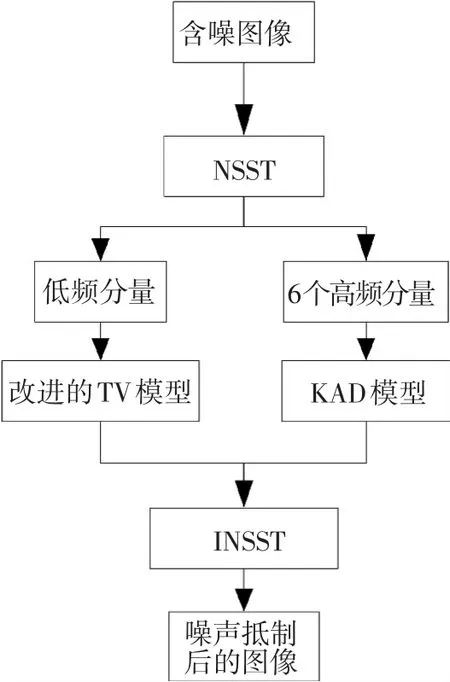
图2 图像噪声抑制算法

Step 3（获取Shearlet系数） 将得到的锥形方向频率分量映射到笛卡尔坐标系，并对其做傅里叶逆变换，获得高频分量的Shearlet系数.本文采用单层NSST，得到了图像低频分量系数Il和6个高频分量系数（Ih1，Ih2，Ih3，Ih4，Ih5，Ih6）．其中，拉普拉斯滤波器选择“maxflat”，进行方向剖分的窗函数为“Meyer”.

Step 4（低频分量噪声抑制） 图像经Shearlet分解后的低频分量包含图像信号的主要能量，同时包含少量的噪声.若不进行处理，会降低图像质量，影响视觉效果；若采用传统的滤波方法，可能会损失图像部分信息，甚至产生阶梯效应.因此，本文采用对图像细节特征保持较好的ITV扩散模型处理低频分量，得到噪声抑制后的低频分量I′l，扩散方程为式（8），时间步长为0.1，当迭代前后两幅图像的均方误差小于0.05时，停止迭代.

Step 5（高频分量噪声抑制） 图像的高频分量包含了较为丰富的细节信息和大量的噪声，对6个高频分量系数分别采用KAD模型进行扩散处理，得到噪声抑制后的高频分量（I′h1，I′h2，I′h3，I′h4，I′h5，I′h6），扩散模型采用式（4），扩散方程为式（5），最大迭代次数为15，当迭代前后两幅图像均方误差小于0.15时，停止迭代，式（6）中采用的核函数其中σ＝3 000．

Step 6 综合处理后的低频分量I′l和高频分量（I′h1，I′h2，I′h3，I′h4，I′h5，I′h6），利用逆NSST（inverse NSST，INSST）得到噪声抑制后的图像.

4 结果与分析

针对本文提出的方法，对大量图像进行了噪声抑制实验，给出了本文方法及近年来提出的基于小波阈值收缩结合全变差的噪声抑制方法（WSTV）、基于复Contourlet域非线性扩散的噪声抑制方法（CCPMTV）、自适应Shearlet域约束的全变差图像噪声抑制方法（SHTV）的噪声抑制结果对比，并依据主观视觉效果及峰值信噪比、结构相似度等客观定量指标对上述4种方法进行了评价与比较.实验参数设置如下：WSTV采用单层Haar小波分解，低频采用时间步长为0.2的TV扩散，高频采用自适应阈值收缩；CCPMTV采用单层复Contourlet分解，滤波器选择“antonini”和“qshift-a”，低频处理采用TV扩散，其时间步长为0.2，迭代终止条件为迭代前后的图像均方误差小于0.01，高频采用PM扩散模型进行处理，迭代次数为30；SHTV采用单层频域离散Shearlet分解，高频分量进行自适应阈值收缩处理，使用的自适应收缩函数为Sτ（χ）＝sign（χ）0），其中：sign（χ）为符号函数；σn、σχ分别为噪声、信号的标准差；TV扩散的最小迭代次数为20次；迭代步长为1／20.本文的噪声抑制实验均是在Intel（R）Core（TM）2，主频2.0 GH，内存2 GB，处理程序为Matlab R2009a的环境下进行的.

现以3幅图像为例加以说明.图3～5分别给出了Lena图像、焊接缺陷图像及织物疵点图像，属于纹理较为复杂的一类图像.图3（c）～图5（c）为使用WSTV所得到的噪声抑制后图像；图3（d）～图5（d）为使CCPMTV所得到的噪声抑制后图像；图3（e）～图5（e）为使用SHTV所得到的噪声抑制后图像；图3（f）～图5（f）为使用本文方法所得到的噪声抑制后图像.噪声是均值为0、方差＝20的高斯白噪声.

图3 Lena图像的噪声抑制

在WSTV方法中，由于对高频分量采用的阈值收缩方法，易发生噪声“过扼杀”或抑制不完全等情况，图4（c）～图6（c）的背景图像中依然残留大量的噪声，图5（c）和图6（c）中的咬边缺陷和缺经疵点上仍覆盖了部分噪声，且缺陷和疵点的细节部分模糊不清；经复Contourlet变换分解后，图像的方向信息被捕捉得更为准确，且高、低频均采用了扩散处理，与图4（c）～图6（c）相比，图4（d）～图6（d）的背景部分更为平滑，但由于图像分解后高频方向数仍受限于分解尺度，且采用TV扩散易丢失细小边缘，PM扩散抵抗强噪声的能力较弱，因此，图4（d）～图6（d）存在一定的“阶梯效应”，如Lena图像的肩部曲线不够平滑，焊接缺陷和织物疵点图像中背景被过度平滑，损失了部分纹理信息.由于采用了Shearlet变换，图像分解时方向性有了更多的选择，相比于CCPMTV方法，图4（e）～图6（e）在背景处的纹理更为清晰，但仍有伪Gibbs效应存在，由于高频分量采用了阈值收缩方法，残留了少量噪声.本文方法采用了具有平移不变性的NSST，弥补了Shearlet变换的不足，低频分量采用的ITV有效地消除了阶梯效应，高频分量采用的KAD抑制噪声的能力更强，得到的图4（f）～图6（f）中噪声去除得最为彻底，细节纹理等保留得更为完整，视觉效果最佳.

图4 焊接缺陷图像的噪声抑制

图5 织物疵点图像的噪声抑制

图6 纸张缺陷图像的噪声抑制

表1给出了Lean图像在不同噪声强度下使用4种方法得到的峰值信噪比和图像结构相似度.其中峰值信噪比越高，说明噪声抑制性能越好；结构相似度更为接近人眼主观感受，其值越接近于1，表示去噪效果越好，噪声抑制后图像的亮度、对比度和纹理结构越接近于原始图像.峰值信噪比和结构相似度的计算公式为

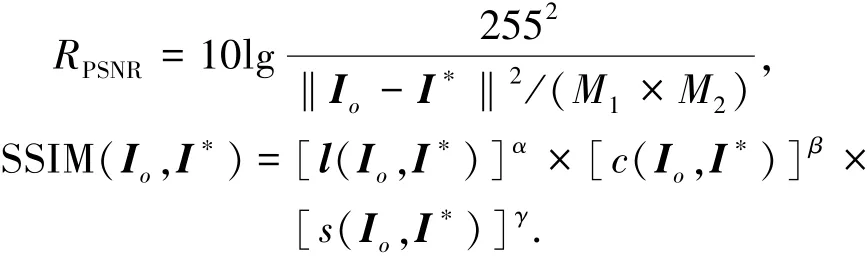
式中：Io、I∗分别为原始图像、噪声抑制后的图像；l（·）、c（·）、s（·）分别为亮度、对比度和结构比较函数，其中α＝β＝γ＝1．

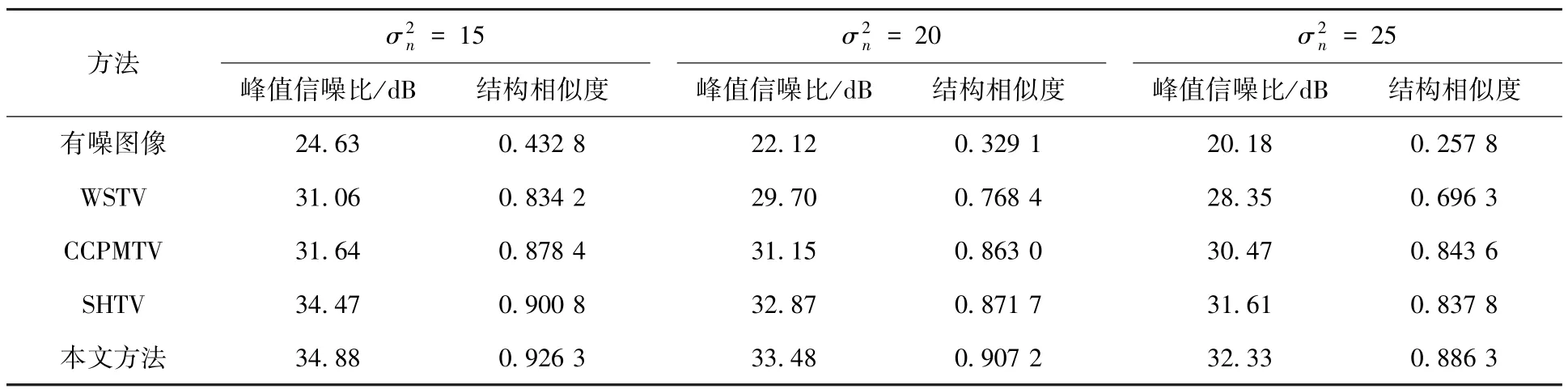
表1 4种噪声抑制方法的性能比较

从表1可以看出，在3种噪声强度下使用本文方法所得图像的峰值信噪比均是最高的，其中在噪声方差σ2n＝20时，峰值信噪比较WSTV、CCPMTV和SHTV分别有3.78、2.33和0.61 dB的增长.由于本文方法高、低频分量均采用了扩散处理，且低频分量采用的ITV扩散有效地避免了TV扩散可能出现的假边缘，高频分量采用的KAD模型的噪声抑制能力更强，即使在强噪声污染时（σ2n＝25），依然能有效地抑制噪声.另外，本文方法的结构相似度也是4种方法中最高的，有效保留了图像的细节和纹理信息.

图6、7还给出了纸张缺陷和铁轨表面缺陷图像的噪声抑制效果图，从图6、7可以看出，本文方法的噪声抑制效果最好，有效地保留了图像中缺陷的细节和纹理信息，为工程中后期缺陷的准确识别及分类奠定了良好的基础.

图7 铁轨表面缺陷图像的噪声抑制

5 结 论

1）本文提出了一种基于NSST和核各向异性扩散的图像噪声抑制方法.利用NSST对含噪图像进行了多尺度分解，克服了Shearlet易产生的伪吉布斯效应，更为丰富地提取了图像的方向信息，更精确地捕获了图像的边缘细节.

2）低频分量采用了ITV扩散进行处理，克服了TV扩散易产生的阶梯效应，改善了图像视觉效果，提高了扩散的效率.

3）对高频分量进行了KAD处理，利用核理论将图像噪声和边缘非线性可分问题转化为特征空间的线性可分问题，有效地提升了噪声抑制能力，增强了扩散的鲁棒性.

4）与近年来提出的WSTV、CCPMTV和SHTV相比，本文方法噪声去除得更为彻底，而且能够更为有效地保留图像的边缘、纹理等细节信息，噪声抑制后的图像主观视觉效果最佳，且在峰值信噪比和结构相似度等客观定量指标上均优于其他3种方法.

［1］SHAO Jiaxin，DU Dong，SHI Han，et al.A fast and adaptive method for automatic weld defect detection in various real⁃time X⁃ray imaging systems［J］.China Welding（English Edition），2012，21（1）：8-12.

［2］KUMAR A.Computer⁃vision⁃based fabric defect detection：a survey［J］.IEEE Transactions on Industrial Electronics，2008，55（1）：348-363.

［3］易子麟，尹东，胡安洲，等.基于非局部均值滤波的SAR图像去噪［J］.电子与信息学报，2012，34（4）：950-955.

［4］张小华，陈佳伟，孟红云，等.基于方向增强邻域窗和非下采样Shearlet描述子的非局部均值图像去噪［J］.电子与信息学报，2011，33（11）：2634-2639.

［5］唐世伟，林君.小波变换与中值滤波相结合图像去噪方法［J］.哈尔滨工业大学学报，2008，40（8）：1334-1336.

［6］PERONA P，MALIK J.Scale⁃space and edge detection using anisotropic diffusion［J］.IEEE Transactions on Pattern AnalysisandMachineIntelligence，1990，12（7）：629-639.

［7］RUDIN L I，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms［J］.Physica D：Nonlinear Phenomena，1992，60（1／4）：259-268.

［8］DO M N，VETTERLI M.The contourlet transform：an efficient directional multiresolution image representation［J］.IEEE Transactions on Image Processing，2005，14（12）：2091-2106.

［9］吴一全，纪守新，尹丹艳.基于NMF、ICA和复Contourlet变换的红外小目标检测［J］.宇航学报，2011，32（8）：1833-1839.

［10］CUNHA A L，ZHOU Jianping，DO M N.The nonsubsampled contourlet transform：Theory，design，and application［J］.IEEE Transactions on Image Processing，2006，15（10）：3089-3101.

［11］吴亚东，孙世新.基于二维小波收缩与非线性扩散的混合图像去噪算法［J］.电子学报，2006，34（1）：163-166.

［12］吴一全，侯雯，吴诗婳.基于复Contourlet域非线性扩散的图像去噪［J］.电路与系统学报，2012，17（6）：111-116.

［13］EASLEY G，LABATE D，LIM W Q.Sparse directional imagerepresentationsusingthediscreteshearlet transform［J］.Applied and Computational Harmonic Analysis，2008，25（1）：25-46.

［14］朱华生，邓承志.自适应Shearlet域约束的全变差图像去噪［J］.计算机工程，2013，39（1）：221-224.

［15］林云莉，赵俊红，朱学峰，等.改进的TV模型图像修复算法［J］.计算机工程与设计，2010，31（4）：776-779.

［16］YU Jinhua，WANG Yuanyuan，SHEN Yuzhong.Noise reduction and edge detection via kernel anisotropic diffusion［J］.PatternRecognitionLetters，2008，29（10）：1496-1503.

［17］LABATE D，LIM W Q，KUTYNIOK G，et al.Sparse multidimensional representation using shearlets［C］／／Proceedings of the SPIE.Beijing：SPIE，2005，5914：254-262.

［18］EASLEY G R，LABATE D，COLONNA F.Shearlet⁃based totalvariationdiffusionfordenoising［J］.IEEE Transactions on Image Processing，2009，18（2）：260-268.

［19］刘建磊，冯大政.结合核方法的选择性各向异性扩散去噪算法［J］.中国图象图形学报，2011，16（11）：1975-1982.

［20］BLACK M J，SAPIRO G，MARIMONT D H，et al. Robust anisotropic diffusion［J］.IEEE Transactions on Image Processing，1998，7（3）：421-432.

（编辑 张 红）

Noise suppression of image based on nonsubsampled shearlet transform and kernel anisotropic diffusion

WU Yiquan1，2，3，YE Zhilong1，WAN Hong1，GANG Tie2

（1.College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，210016 Nanjing，China；2.State Key Laboratory of Advanced Welding and Joining（Harbin Institute of Technology），150001 Harbin，China；3.Shenzhen Key Laboratory of Urban Rail Traffic（Shenzhen University），518060 Shenzhen，China）

To suppress noise of image more efficiently and further improve image visual effects，a noise suppression method of image based on shearlet transform and kernel anisotropic diffusion is proposed.Firstly，a noisy image is decomposed by nonsubsampled shearlet transform（NSST）.Then the obtained low⁃frequency component and high⁃frequency components are processed by improved total variation（ITV）diffusion and kernel anisotropic diffusion（KAD），respectively.Finally，the noise suppressed image is obtained by synthesizing diffused low⁃frequency component and high⁃frequency components through inverse nonsubsampled shearlet transform（INSST）.Experimental results are given，in terms of subjective visual effect and two quantitative evaluation indicators such as peak signal to noise ratio（PSNR），structural similarity（SSIM），a comparison is made with three recent proposed noise suppression methods based on wavelet threshold shrinkage and TV，based on nonlinear diffusion in complex contourlet domain，and using TV with adaptive shearlet domain restraint.A large number of experimental results show that the proposed method has stronger noise suppression ability and preserves edge and detail information more completely.

image processing；noise suppression；nonsubsampled shearlet transform；improved total variation diffusion；kernel anisotropic diffusion

TN911.73

：A

：0367-6234（2014）11-0076-08

2013-07-30.

国家自然科学基金（60872065）；先进焊接与连接国家重点实验室开放基金（AWPT-M04）；深圳市城市轨道交通重点实验室开放基金（SZCSGD201306）；江苏省制浆造纸科学与技术重点实验室开放课题（201313）；纺织面料技术教育部重点实验室开放基金（P1111）.

吴一全（1963—），男，教授，博士生导师；刚 铁（1952—），男，教授，博士生导师.

吴一全，nuaaimage＠163.com.