光纤捷联惯导系统的双轴旋转调制方案

于飞，阮双双

（1.哈尔滨工程大学理学院，黑龙江哈尔滨150001；2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

光纤捷联惯导系统的双轴旋转调制方案

于飞1，阮双双2

（1.哈尔滨工程大学理学院，黑龙江哈尔滨150001；2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

针对目前常用的双轴旋转方案对惯性器件的标度因数误差和安装误差的调制不完全的缺点，提出了一种改进的双轴旋转调制方案。该方法通过逐步分析系统的误差传播特性，设计每一转动次序的转轴和转动方向，使前后次序残余的器件误差互相抵消，从而提高了双轴旋转调制的效果，满足了捷联惯导系统自主导航精度的要求。对实验室常用的双轴旋转调制方案和改进的方案进行了对比研究，仿真和试验结果表明，改进的双轴旋转方案的速度误差和定位误差曲线的周期振荡幅值较原方案显著减小，而且误差曲线整体发散的速度也非常缓慢。

光纤捷联惯导系统；惯性器件误差；双轴旋转方案；残余误差；周期振幅；自主导航；系统精度

捷联惯性导航系统中，在惯性器件精度达到一定要求后，采用补偿惯性器件偏差的方法来进一步改善系统的性能是实现更高精度导航的一个途径［1-2］。Sperry Marine公司早在20世纪80年代初就投入舰船用捷联惯导系统研制工作中，并于1987～1991年陆续推出了MK39 Mod3C［3］、AN／WSN-7B［4］和MK49［5］旋转调制型激光陀螺SINS（strapdown inertial navigation system）。光纤陀螺与激光陀螺相比具有结构组成与制造工艺相对简单、可靠性与精度的潜力更大等许多特点，由Boeing公司［6］领军完成的高精度光纤陀螺SINS中也应用了旋转调制技术，相关的研究工作［7-9］表明旋转调技术也可用于光纤陀螺SINS。双轴旋转调制效果主要取决于方案的设计，根据目前可见参考文献报道，光纤陀螺旋转调制技术的研究主要集中在误差分析［10］、初始对准［11］和系统标定［12］等方面，对双轴旋转调制方案的设计与分析则相对较少。在利用原有的双轴旋转方案［13］在实验室进行双轴导航试验时，导航精度总是难以达到指定水平，尤其是更换了捷联惯导系统中的某个陀螺部件后，再利用原有的双轴旋转方案进行的双轴导航试验，试验结果与陀螺部件更换前的双轴导航试验相比差了很多，而实际上更换的陀螺比原组陀螺性能要高许多。本文的研究工作正是基于上述问题开展的，通过分析双轴旋转调制方案的基本原则，详细研究了最优双轴旋转方案的设计过程与整个方案与系统导航精度之间的关系；最后通过仿真和实验室转台试验验证了改进方案的实用性与优越性。

1 双轴旋转方案设计的基本原则

双轴旋转调制是一项通过转动IMU将惯性测量元件的输出误差调制成周期变化形式的技术。在导航解算的过程中，利用积分运算自动将器件误差平均为零，从而提高系统的导航精度。

双轴旋转SINS的误差方程：

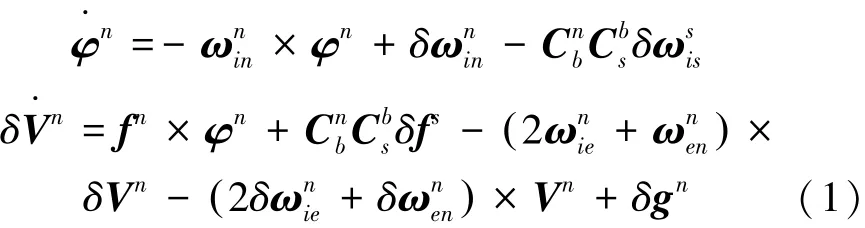
式中：s系表示IMU坐标系，b系表示载体坐标系，n系表示地理坐标系，φ表示误差角，V和δV分别表示速度和速度误差，ω和δω分别表示角速度和角速度误差，f和δf表示比力和加速度计测量误差，δg表示重力偏差，表示从1坐标系到2坐标系的转换矩阵。本文所选取的导航坐标系是地理坐标系，为了分析问题更简洁，文中假设载体坐标系与导航坐标系重合。加速度计误差与陀螺仪误差的调制形式相同，本文就只分析陀螺仪的输出误差的调制过程。

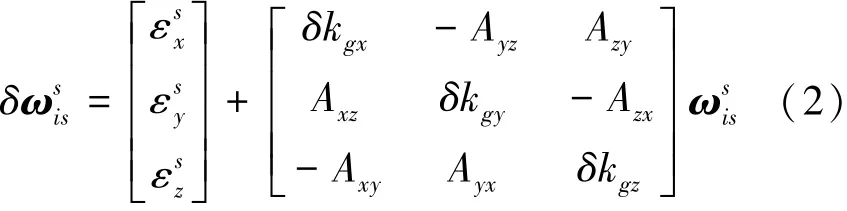
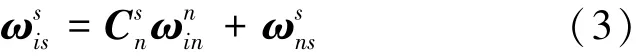
假设初始时刻IMU坐标系与载体坐标系重合，不考虑载体运动速度，则

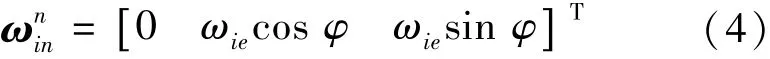
IMU在转动过程中陀螺输出误差角速度δωsis在地理坐标系下的投影为

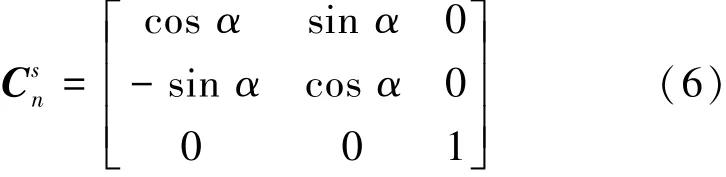
将式（2）和式（6）代入式（5）中，得IMU输出误差在地理坐标系下的投影为

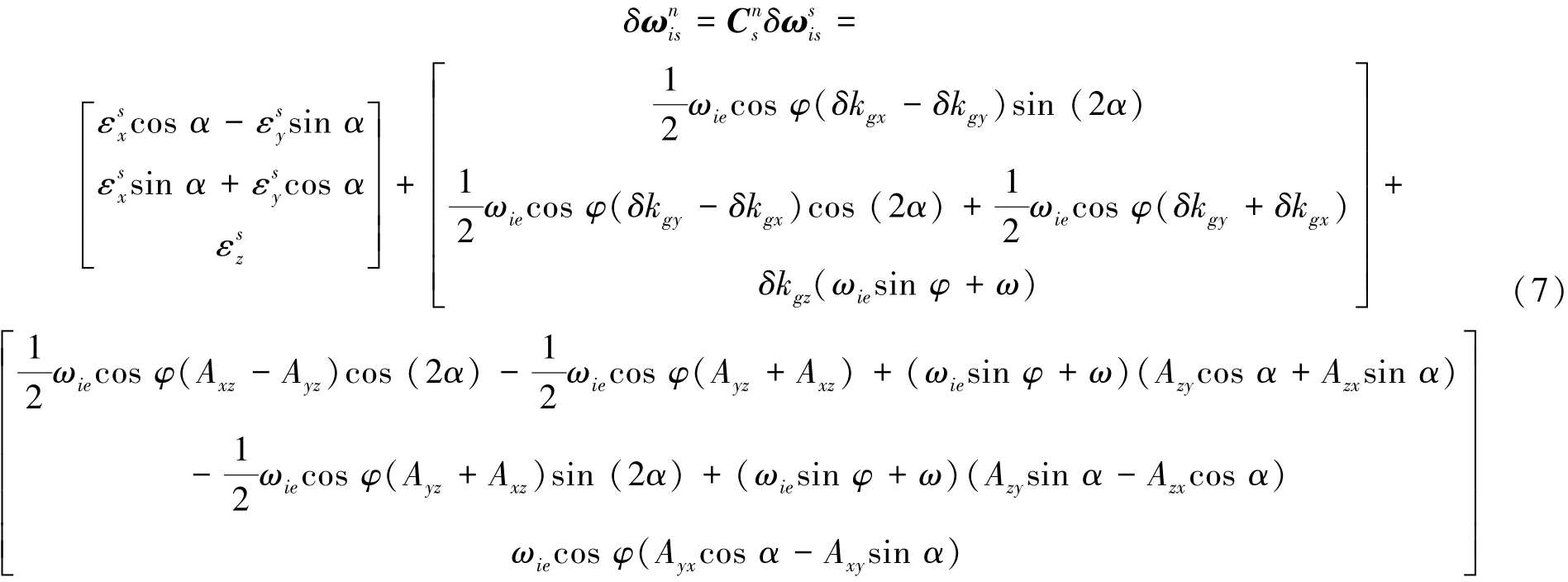
由式（7）可知，在单次的旋转调制过程中，惯性器件的输出误差在地理坐标系下的投影有5种形式：1）常值形式的误差项（以下称为直流分量）；2）被调制为sin α形式的误差项；3）被调制为cos α形式的误差项；4）被调制为sin（2α）形式的误差项；5）被调制为cos（2α）形式的误差项。

对式（7）在α∈0，π[]范围进行积分，将该过程分解为对式（7）中5种形式的误差单独积分，其结果如下：

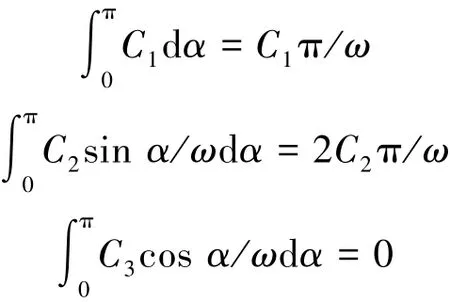
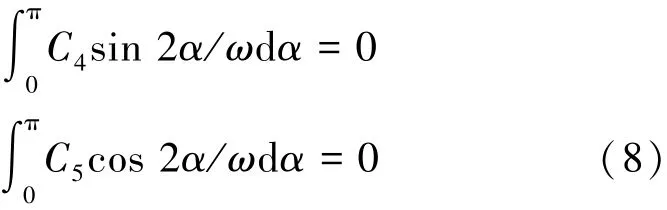
式中：Ci（i＝1，2，3，4，5）表示由陀螺常值漂移、安装误差和标度因数误差组成的常系数。由式（8）得，δ在单次转动周期内积分，只有1）和2）两种形式的误差项不能被平均为零，因而被作为残余误差持续累积。好的双轴旋转调制方案必须保证残余误差在后续转动过程中可以相互抵消，因此残余误差的传播特性是设计旋转方案的关键。

2 改进的双轴旋转方案设计

在双轴旋转方案中，2根转轴交替旋转，新IMU坐标系与原IMU坐标系的三轴在每次转过180°后仍然互相平行，因此同转轴的前后两次旋转具有相似的残余误差分量。第1次转动次序确定后，首先考虑同转轴的第2次转动的方向选取问题；在1、3次序确定后，接下来考虑2、4次序的方向选取问题；在前4次序设计完成后，最后考虑双轴旋转调制方案的整体关系。

2.1 同轴旋转方向选取

旋转调制方案的好坏取决于逐次转动过程中残余误差之间互相抵消的效果，残余误差由直流分量和被调制为sin α形式的误差组成。IMU在次序1绕zs轴正向转动180°，通过式（7）可得此次转动过程的残余误差在地理坐标系各轴分量见表1。次序1确定后，首先考虑次序3的转动方向问题。假设1次序3正转，则此次转动方向余弦矩阵（不受次序2的转动方向影响）为

表1 次序1的残余误差（正转）Table 1 The residual errors of order one（positive）

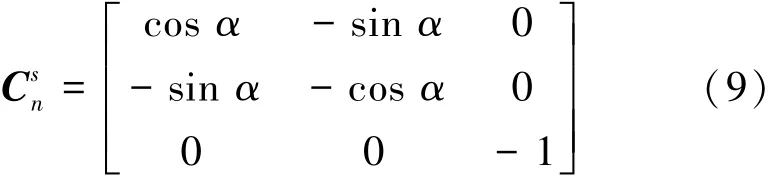
表1和表2中，符号相反的同轴分量可以互相抵消。因此东向残余误差中，安装误差与地球自转角速度分量引起的常值误差以及地球自转角速度分量与安装误差耦合引起的sin α项可以被抵消；北向残余误差中，被调制成sin α形式的东向陀螺漂移误差以及ω与安装误差耦合误差可以被抵消；天向残余误差中，天向陀螺漂移引起的常值误差以及ω与标度因数误差耦合误差可以被抵消。

假设2次序3是反转，转动方向余弦矩阵为

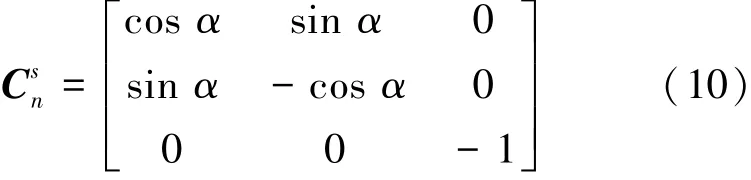
利用式（2）、式（5）和式（10），获得IMU输出误差在地理坐标系下的投影，并将残余误差列入表3中。对比表1和表3，东向残余误差中，被调制成sin α形式的北向陀螺漂移可以被抵消；北向残余误差中，地球自转角速度分量以及ω与安装误差的耦合误差可以被抵消；天向残余误差中，天向陀螺漂移引起的常值误差和地球自转角速度分量与安装误差的耦合误差可以被抵消。

表2 次序3的残余误差（正转）Table 2 The residual errors of order three（positive）

表3 次序3的残余误差（反转）Table 3 The residual errors of order three（negative）

假设1可以更多地抵消ω与安装误差和标度因数误差耦合引起的残余误差在地理坐标轴上的分量；而假设2中ω引起的误差分别在地理坐标系的东向和天向再次积累。考虑到ω远大于地球自转角速度，由ω引起的误差远大于其他残余误差，因此次序3正转更有助于提高系统实时精度，尤其是在ω较大时，假设1的优势将更加明显。图1是针对假设1和假设2设计的4次序转动方案仿真对比。假设1：zs＋，ys－，zs＋，ys－；假设2：zs＋，ys－，zs－，ys＋。

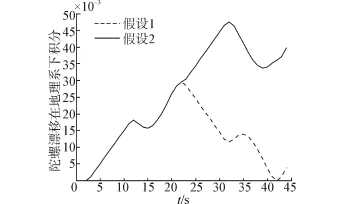
图1 假设1与假设2对比图Fig.1 The contrast of hypothesis 1 and hypothesis 2

结论1：在双轴旋转方案中，每一对同轴旋转的转动方向都必须相同，从而保证ω引起的误差能够在2次同轴旋转过程中完全抵消。

2.2 异轴旋转方向选取

在次序1的转轴和旋转方向选定以后，次序2的转轴是固定的，而次序2转动方向是决定双轴旋转调制效果的关键。

假设3次序2绕ys轴反转180°，转动方向余弦矩阵为

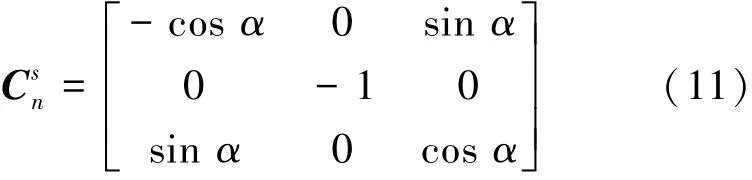
利用式（2）、式（5）和式（11），可获得IMU输出误差在地理坐标系下的投影，将投影结果中残余误差项列入表4中。

表4 次序2的残余误差（反转）Table 4 The residual errors of order two（negative）

根据结论1，次序4也绕ys轴反转180°，转动方向余弦矩阵为

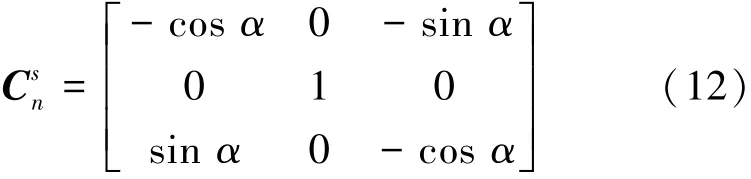
同理利用式（2）、式（5）和式（12），可获得残余误差在地理坐标系各轴上的分量见表5。

表5 次序4的残余误差（反转）Table 5 The residual errors of order four（negative）

对比表4和表5，在地理坐标系的东向、北向和天向的残余误差分量中，与ω耦合的误差项均可互相抵消，这再一次验证了结论1的正确性。

对比表1和表4，东向残余误差中，被调制成sin α形式的陀螺漂移误差项符号相反；北向残余误差中，地球自转角速度分量与安装误差的耦合误差符号相反；天向残余误差中，地球自转角速度分量与安装误差的耦合误差也符号相反。在实际系统中，3个陀螺的误差系数不等，因此表1和表4中对应的符号相反的残余误差项只能局部相消。如果系统中3个陀螺仪的性能相差不大，残余误差系数对应相减可以使误差基本都能抵消，从而提高导航系统的精度。因此随意更换系统中某个惯性测量部件对双轴导航系统来说更有可能降低系统的导航精度。比较表2和表5也有相同的结论。

假设4次序2绕ys轴正转180°，转动方向余弦矩阵为

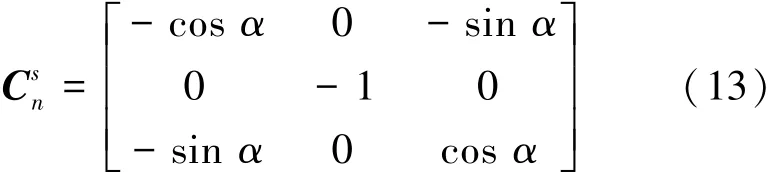
同理利用式（2）、式（5）和式（13），可获得残余误差在地理坐标系各轴上的分量见表6。

表6 次序2的残余误差（正转）Table 6 The residual errors of order two（positive）

表6中由ω引起的残余误差和一些较大的直流分量误差可与次序4的正转后的残余误差抵消，此处不再给出系统在次序4绕ys轴正转180°的残余误差表。比较表1和表6，不考虑同轴对之间被抵消的残余误差项，其他残余误差项符号完全相同。

因此假设3能部分抵消同轴对之间无法消除的残余误差，从而提高系统精度；假设4对系统精度没有改善。图2是在旋转方案结论1的基础上针对假设3与假设4设计的4次序转动仿真结果对比。假设3是zs＋，ys－，zs＋，ys－；假设4是zs＋，ys＋，zs＋，ys＋。

结论2：在双轴旋转方案中，每一对异轴旋转的转动方向都必须相反，从而进一步抵消系统中的残余误差。

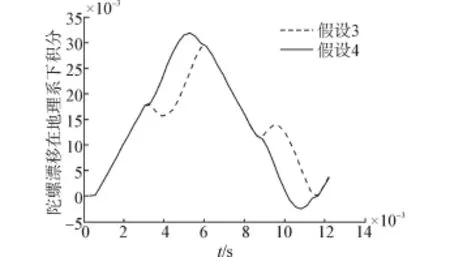
图2 假设3与假设4对比图Fig.2 The contrast of hypothesis 3 and hypothesis 4

2.3 转动次序整体关系

在结论1和结论2的基础下，可确定双轴旋转方案的前4次序。IMU经过4次转动后，回到原位置a。在前4次旋转中，惯性器件的输出误差在地理坐标系下的分量仍不能完全调制为零。如果次序5～8的转轴与次序1～4的相同，转动方向相反，由假设2和假设4中对应的残余误差表可知，前8次序中地球自转角速度分量与陀螺标度因数误差以及安装误差的耦合项的积分结果将持续积累。如果安装误差为2″，标度因数误差为10－5，地理纬度为45.77°，则地球自转角速度分量与陀螺标度因数误差以及安装误差的耦合项等效于给东向、北向和天向各自加0.000 1（°）／h的常值“陀螺漂移”，它们将随时间增长，给系统造成较大的误差。为了进一步抵消前4次序中地球自转角速度分量引起的误差，设计次序5～8的转轴和转动方向如图4所示。

在实际的系统中，3个陀螺仪和3个加速度计的差异会比较大，导致前8次序中的残余误差不能完全互相抵消，给系统补一组对称的转动序列使其与前8次序共同构成16次序双轴旋转方案，次序9～16的转动方案图如图5所示。

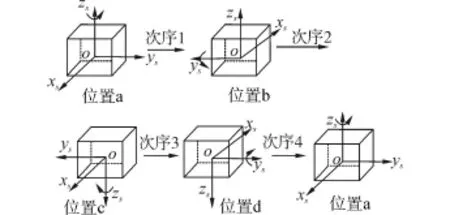
图3 次序1到次序4转动方案图Fig.3 The rotating scheme from order 1 to order 4

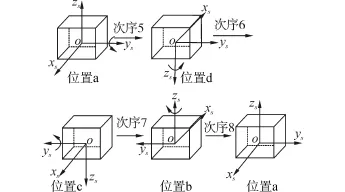
图4 次序5～8转动方案图Fig.4 The rotating scheme from order 5 to order 8

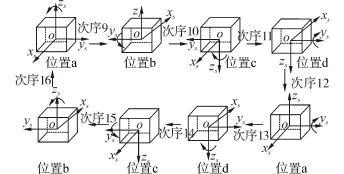
图5 次序9到次序16转动方案图Fig.5 The rotating scheme from order 9 to order 16

图3 ～5给出了改进的16次序双轴旋转方案的转位图。将常用的双轴旋转方案［13〛整理到表7中。

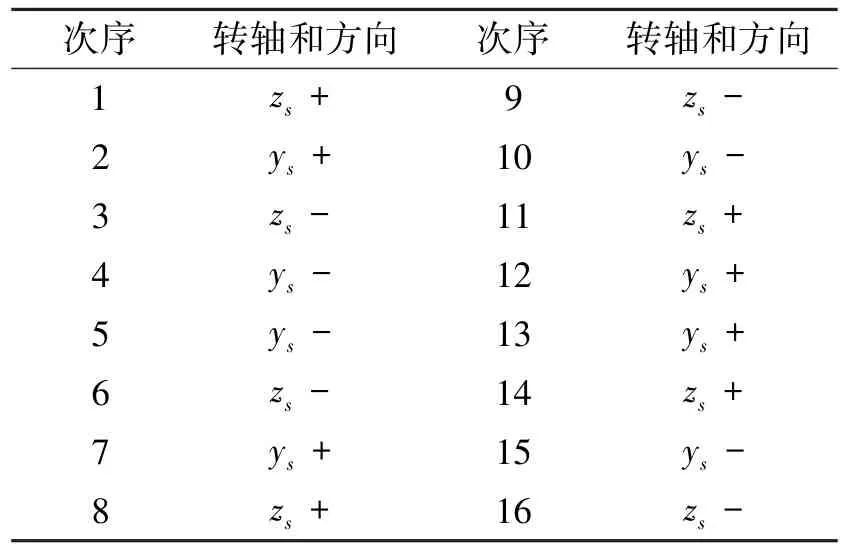
表7 常用的双轴旋转方案Table 7 The commonly used dual-axis rotating scheme

3 仿真与试验分析

根据上述改进的方案给出仿真验证，仿真器件误差值如下：陀螺常值漂移为0.001（°）／h；加速度计零偏为5×10－5g；陀螺和加速度计标度因数误差为10－5；陀螺和加速度计安装误差角为2″，转动角速度为20（°）／h，在每个位置停止45 s，将改进的方案与常用方案比较，结果如图6～8。

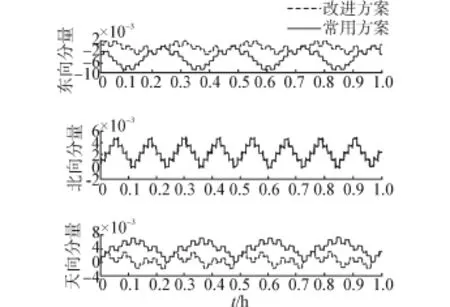
图6 陀螺仪误差在地理系下积分Fig.6 The integral of gyro errors

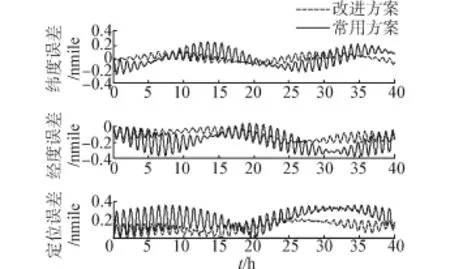
图7 定位误差仿真Fig.7 Position errors in simulation

仿真结果中，改进方案和常用方案的定位误差最大值分别为0.4 nmile和0.74 nmile；速度误差的最大值分别为0.5 m／s和1 m／s。图6是陀螺仪误差输出值在地理坐标系下的投影随时间积分的结果，改进方案和常用方案中的器件误差都可以被周期的调制平均为零，而改进方案的优势在于，器件误差积分曲线的振荡幅度小，实时导航精度更高。

为了进一步验证改进方案的优越性，利用实验室的高精度三轴转台和教研室自研的光纤陀螺SINS进行了多次双轴旋转试验，实物见图9。实验室所用的高精度三轴转台的性能指标如表8。

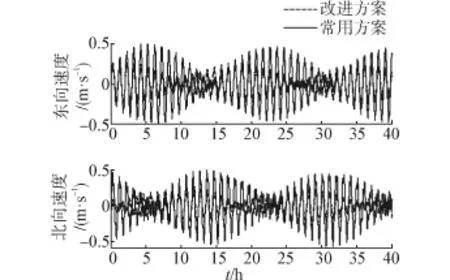
图8 速度误差仿真Fig.8 Velocity errors in simulation

图9 3转台和光纤捷联系统Fig.9 SGT-3 turntable and fiber SINS

表8 SGT-3型惯性测试转台主要性能指标Table 8 Performance indexes of SGT-3 turntable

双轴旋转试验参数如下：转动角速度为20（°）／h，在每个位置停止45 s，系统开机后预热1 h。图10～11是实验室24 h双轴旋转试验的结果，改进方案和常用方案的定位误差最大值分别为2.3 nmile和4.8 nmile；速度误差的最大值分别为2.8 m／s和7 m／s，改进方案明显优于目前常用方案。

对系统引入多普勒计程仪的速度进行阻尼，其结果如图12～13。由图12和图13结果可得，引入外速度对系统阻尼以后，改进方案和常用方案的定位误差最大值分别为1.5 nmile和3 nmile；速度误差的最大值分别为0.5 m／s和2 m／s。阻尼后改进方案与常用方案的精度都有一定的改善，由于改进方案中器件误差已经基本被调制平均，因此外速度的引入对其精度的改进作用有限。

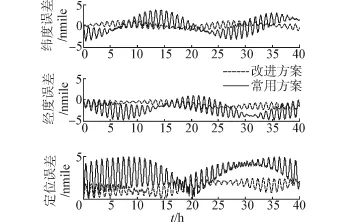
图10 定位误差试验Fig.10 Position errors in experiment

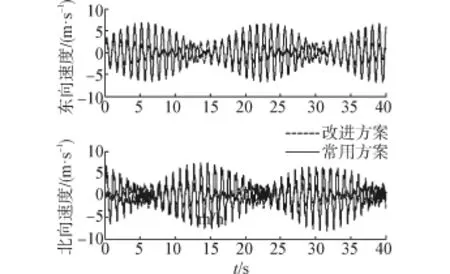
图11 速度误差试验Fig.11 Velocity errors in experiment

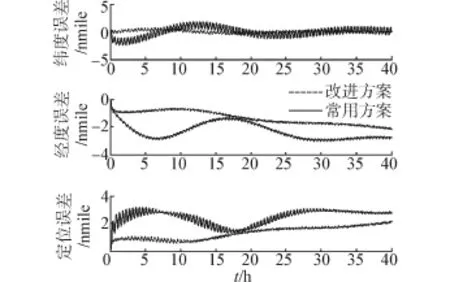
图12 阻尼定位误差试验Fig.12 Position errors in experiment with damp

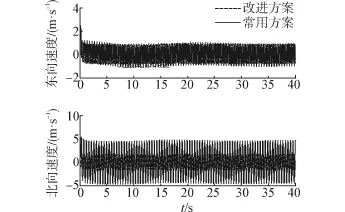
图13 阻尼速度误差试验Fig.13 Velocity errors in experiment with damp

4 结束语

为了解决光纤陀螺SINS中因原双轴旋转调制方案不足而引起系统自主导航精度不理想的问题，本文通过分析残余误差的传播特性，设计了一种改进的双轴旋转方案。分析结果表明系统精度不仅取决于双轴旋转调制方案，还取决于惯性测量元件的性能参数之间的一致性。从仿真和实验结果可以看出，改进的双轴旋转调制方案的定位误差由原方案中的4.8 nmile减小到2.3 nmile，阻尼后定位误差由原方案中的3 nmile减小到1.5 nmile，这说明了改进的双轴旋转方案能提高系统的精度。本文的研究内容为双轴旋转式捷联惯导系统的设计提供一定的参考价值。

［1］RANDALL K C，MICHAEL E A，LEROY O T，et al.Proposed IEEE inertial systems terminology standard and other inertial sensor standards［C］／／IEEE PLANS：Position Location and Navigation Symposium.Monterey，USA，2004：83-90.

［2］LEVINSON E.Accuracy enhancement techniques to the marine ring laser inertial navigation［J］.Navigation，1987，34（1）：64-87.

［3］MARLAND P.The NATO ships inertial navigation system（SINS）［J］.Joumal of Naval Engineering，1992，33（3）：688-700.

［4］TERRT T，EMANUEL L.The AN／WSN-7B marine gyrocompass navigator［C］／／Proceedings of the 2000 National Technical Meeting of the Institute of Navigation.London，2000：348-357.

［5］LAHHAN J I，BRAZELL J R.Acoustic noise reduction in the MK49 ship's inertial navigation system（SINS）［C］／／IEEE PLANS：Position Location and Navigation Symposium.Monterey，USA，1992：32-39.

［6］HAYS K M，SCHMIDT R G，WILSON W A.A submarine navigator for the 21st century［C］／／Control＆Communications and Strategic Systems.Anaheim，USA，2002：121-127.

［7］SHIBASHI S，TSUKIOKA S，YOSHIDA H.Accuracy improvement of an inertial navigation system brought about by the rotational motion［C］／／OCEANS 2007-Europe.Aberdeen，Scotland，2007：1-5.

［8］LI An，QIN Fangjun，CHANG Guobin.Improved precision of strapdown inertial navigation system brought by dual-axis continuous rotation of inertial measurement unit［C］／／2010 2nd International Asia Conference on Informatics in Control，Automation and Robotics.［S.l.］，2010：284-287.

［9］SUN Wei，GAO Yang.Fiber-based rotary strapdown inertial navigation system［J］.Optical Engineering，2013，52（7）：1-12.

［10］孙尧，王庭军，高延滨，等.旋转式捷联惯导系统解算结构［J］.中国惯性技术学报，2013，21（1）：10-15.SUN Yao，WANG Tingju，GAO Yanbin，et al.Computation structure of rotating strapdown INS［J］.Journal of Chinese Inertial Technology，2013，21（1）：10-15.

［11］郝燕玲，张义，孙枫，等.单轴旋转式捷联惯导方位对准研究［J］.仪器仪表学报，2011，32（2）：309-315.HAO Yanling，ZHANG Yi，SUN Feng，et al.Analysis of single-axial rotation SINS azimuth alignment［J］.Chinese Journal of Scientific Instrument，2011，32（2）：309-315.

［12］ZHU Lufeng，ZHANG Chunxi.The fine system level calibration technique of size effect error for the fiber-SINS［C］／／Manufacturing Science and Technology.Singapore，2012：2060-2065.

［13］YUAN Baolun，LIAO dan，HAN songlai.Error compensation of an optical gyro INS by multi-axis rotation［J］.Meas Sci Technol，2012，23（2）：1-9.

Dual-axis rotating scheme for fiber strapdown inertial navigation system

YU Fei1，RUAN Shuangshuang2
（1.College of Science，Harbin Engineering University，Harbin 150001，China；2.College of Automation，Harbin Engineering University，Harbin 150001，China）

In order to further counteract the incomplete modulation to inertial sensors'scale errors and installation errors in the commonly used dual-axis rotating scheme at present，an improved dual-axis rotating scheme was proposed.By analyzing the propagation characteristics of system errors stage by stage，the rotation axis and direction of each rotation were designed respectively so as to counteract the residual errors of device in sequence，thereby improving the modulating effects of dual-axis rotating and meeting the self-navigation accuracy requirements of SINS（strapdown inertial navigation system）.The proposed scheme was compared with the commonly used scheme in laboratory，and simulation and experiment results showed that the amplitude of the improved scheme's velocity errors and position errors curve is remarkably smaller than that of the commonly used scheme，and the errors'overall divergence speed is very slow.

fiber strapdown inertial navigation system；inertial sensor errors；dual-axis rotating scheme；residual error；periodical amplitude；self-navigation；system accuracy

10.3969／j.issn.1006-7043.201312025

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201312025.html

U666.1

A

1006-7043（2014）12-1536-07

2013-12-10.网络出版时间：2014-12-02.

国家自然科学基金资助项目（51379047）.

于飞（1974-），男，教授，博士生导师；阮双双（1988-），女，硕士研究生.

阮双双，E-mail：Ruanss_hrbeu＠163.com.